Содержание
Введение
1. Теоретическая часть
1.1. Однофакторный дисперсионный анализ
1.2. Линейный множественный регрессионный анализ
1.3. Множественный корреляционный анализ
2. Аналитическая часть
2.1. Сбор и первичная обработка данных
2.2. Дисперсионный анализ
2.3. Построение уравнения множественной регрессии
2.4. Исключение незначимых факторов
3. Заключение
4. Список литературы
5. Приложение
Введение
Анализируя данные, о смертности населения за 2004-2006 год, полученные в Нерюнгринской городской больнице (см. таблицу 1), можно сделать вывод о том, что общий коэффициент смертности, то есть число умерших от всех причин на 1000 человек населения, увеличивается (рис.1).
Показатель смертности на 1000 человек населения
Таблица 1
| 2004 год | 2005 год | 2006 год |
| 7.3 | 7.8 | 8.1 |
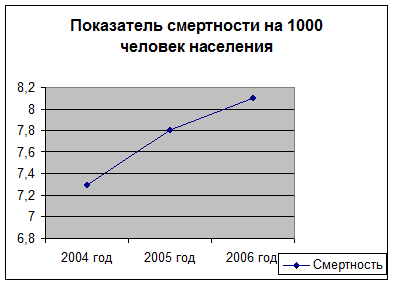
Рисунок 1
Несмотря на повышение рождаемости, демографическая ситуация в Нерюнгринском улусе характеризуется уменьшением численности населения. Главной причиной демографического кризиса является преобладание смертности над рождаемостью. Именно поэтому, чтобы снизить показатель смертности необходимо более детально изучить все причины и факторы, приводящие к ее увеличению. Несомненно, в изучении причин, важно исследование значимости отдельных нозологических форм заболеваний. Зная, какие заболевания приводят чаще всего к летальному исходу, можно разработать программу профилактических работ направленную на уменьшение числа данных заболеваний и предотвращения их дальнейшего развития на раннем этапе.
Цель: определение видов заболеваний оказывающих наибольшее влияние на показатели летальности, основываясь на статистике смертности населения Нерюнгринского улуса по классам болезней и возрастам за 2006 год.
Задачи:
1. сбор статистических данных необходимых для определения закономерности изменения смертности по причинам заболеваний;
2. проведение однофакторного дисперсионного анализа, с целью определения влияния различных болезней на общее количество смертности населения;
3. исключение отдельных факторов, оказывающих незначительное влияние;
4. построение уравнения множественной регрессии, отражающего соотношение между смертностью и различными классами заболеваний.
Теоретическая часть
Аналитическая часть
Дисперсионный анализ
Методом дисперсионного анализа, выясним, оказывает ли влияние различные заболевания на показатель смертности населения. То есть, проверим, выполняется ли гипотеза о равенстве математических ожиданий (Н0: М(Х1) = М(Х2) = … = М(Хр)). Для этого рассчитаем значения наблюдавшихся признаков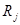 
и значения их квадратов 
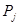для каждого заболевания по формуле (4). Затем, вычислив их сумму, результаты вычислений приведены в таблице 2 [см. Приложение]. Подставим в формулы (5), (6), получим значения общей и факторной дисперсий:
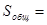13498;
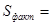5906,7;
Эти значения подставляем в формулу (11) вычисляем остаточную сумму квадратов отклонений наблюдаемых значений группы от своего группового среднего.
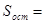7591,5
Теперь мы можем вычислить Fнабл, для этого используем формулу (8), и сравниваем с Fкр, который, смотрится по таблице критерия Фишера – Снедекора [1].
Fнабл = 14, 1090;
Fкр(0,01; 15; 18) = 3,23.
Сравнивая полученные значения, мы делаем вывод о том, что различия между дисперсиями не значимо, то есть фактор (заболевания) оказывает существенное влияние на функцию отклика (смертность). Следовательно, среднее наблюдаемое значение на каждом уровне (групповые средние) различаются значимо.
Заключение
В данной курсовой работе рассмотрены заболевания, влияющие на изменение смертности Нерюнгринского улуса. Были выбраны факторы, методом исключения эффектов, приводящие к высокой смертности. Применяя методы теории вероятностей и математической статистики, было построено уравнение, показывающее зависимость изучаемого явления (смертности) от выбранных факторов (классов заболеваний).
Проведя анализ полученной модели, выяснилось, что наиболее часто приводят к летальному исходу болезни системы кровообращения, таким образом, этот класс заболеваний стоит на первом месте. На втором месте стоят внешние причины заболеваемости и смертности, и на третьем – новообразования.
В заключении, необходимо отметить, что профилактика именно этих заболеваний приведет к уменьшению показателя летальности и позволит преодолеть демографический кризис.
Список литературы
1. Гмурман В.Е. Теория вероятностей и математическая статистика: Учеб. пособие для вузов. - М.: Высш. шк., 1997.
2. Львовский В.Н. Статистические методы построения эмпирических формул: Учеб. пособие для вузов. - М.: Высш. шк., 1988.
3. Вентцель Е.С. Теория вероятностей: Учебник для вузов. - М.: Высш. шк., 1999.
4. «Многомерный статистический анализ на ЭВМ с использованием пакета Microsoft Excel»/М., 1997.
5. «Государственный доклад о состоянии здоровья населения Нерюнгринского улуса в 2006 году»; (редкол.:Вербицкая Л.И. и др.), 2007.
Приложение
Таблица 1
Исходные данные
| XVI | 1 | 1 | 2 | 4 | 11 | 11 | 11 | 16 | 13 | 11 | 15 | 11 | 2 | 5 | 1 | 1 | 0 | 0 |
| XV | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 2 | 0 | 2 | 1 | 0 | 0 | 0 | 0 | 0 |
| XIV | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 5 | 4 | 2 | 4 | 2 | 1 | 3 | 2 |
| XIII | 2 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| XII | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| XI | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| X | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| IX | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| VIII | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 3 | 3 | 4 | 9 | 5 | 3 | 6 | 2 | 0 | 0 | 0 |
| VII | 1 | 0 | 0 | 0 | 0 | 2 | 2 | 1 | 3 | 5 | 6 | 2 | 2 | 1 | 1 | 0 | 1 | 0 |
| VI | 0 | 1 | 0 | 0 | 0 | 4 | 1 | 8 | 17 | 32 | 47 | 41 | 29 | 59 | 35 | 24 | 21 | 8 |
| V | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 2 | 1 | 0 | 1 | 2 | 1 | 1 | 0 | 0 | 0 | 0 |
| IV | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| III | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| II | 0 | 0 | 0 | 0 | 1 | 3 | 0 | 2 | 8 | 14 | 17 | 20 | 11 | 15 | 12 | 3 | 4 | 1 |
| I | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 2 | 0 | 3 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| Количество смертей | 7 | 3 | 3 | 8 | 15 | 29 | 20 | 38 | 50 | 79 | 110 | 88 | 54 | 98 | 56 | 34 | 45 | 20 |
| Возраст | до года | 1-5 | 11-17 | 17-19 | 20-24 | 25-29 | 30-34 | 35-39 | 40-44 | 45-49 | 50-54 | 55-59 | 60-64 | 65-69 | 70-74 | 75-79 | 80-84 | 85 и более |
Таблица 2
Факторный анализ
Возраст
I
II
III
IV
V
VI
VII
VIII
IX
X
до года
0
0
0
0
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
0
1-5
0
0
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
0
0
0
11-17
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
0
0
0
0
0
17-19
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
20-24
0
0
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
25-29
1
1
3
9
0
0
0
0
0
0
4
16
2
4
0
0
0
0
0
0
30-34
0
0
0
0
0
0
0
0
0
0
1
1
2
4
1
1
1
1
0
0
35-39
2
4
2
4
1
1
0
0
2
4
8
64
1
1
3
9
0
0
0
0
40-44
0
0
8
64
0
0
0
0
1
1
17
289
3
9
3
9
0
0
1
1
45-49
3
9
14
196
1
1
1
1
0
0
32
1024
5
25
4
16
0
0
0
0
50-54
0
0
17
289
0
0
0
0
1
1
47
2209
6
36
9
81
0
0
0
0
55-59
1
1
20
400
0
0
0
0
2
4
41
1681
2
4
5
25
0
0
0
0
60-64
0
0
11
121
0
0
0
0
1
1
29
841
2
4
3
9
0
0
0
0
65-69
1
1
15
225
0
0
0
0
1
1
59
3481
1
1
6
36
0
0
1
1
70-74
0
0
12
144
0
0
0
0
0
0
35
1225
1
1
2
4
0
0
0
0
75-79
0
0
3
9
1
1
0
0
0
0
24
576
0
0
0
0
0
0
0
0
80-84
0
0
4
16
0
0
0
0
0
0
21
441
1
1
0
0
0
0
0
0
85 и более
0
0
1
1
0
0
0
0
0
0
8
64
0
0
0
0
0
0
0
0
∑
8
16
111
1479
3
3
1
1
9
13
327
11913
27
91
36
190
1
1
2
2
64
12321
9
1
81
106929
729
1296
1
4
Продолжение таблицы 2
| XI |
XII |
XIII |
XIV | XV |
XVI | ||||||
| R11 | P11 | R12 | P12 | R13 | P13 | R14 | P14 | R15 | P15 | R16 | P16 |
| 0 | 0 | 4 | 16 | 2 | 4 | 1 | 1 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 2 | 4 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4 | 16 |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 11 | 121 |
| 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 11 | 121 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 11 | 121 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 16 | 256 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 13 | 169 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 2 | 4 | 11 | 121 |
| 0 | 0 | 0 | 0 | 0 | 0 | 5 | 25 | 0 | 0 | 15 | 225 |
| 0 | 0 | 0 | 0 | 0 | 0 | 4 | 16 | 2 | 4 | 11 | 121 |
| 0 | 0 | 0 | 0 | 0 | 0 | 2 | 4 | 1 | 1 | 2 | 4 |
| 0 | 0 | 0 | 0 | 0 | 0 | 4 | 16 | 0 | 0 | 5 | 25 |
| 0 | 0 | 0 | 0 | 0 | 0 | 2 | 4 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 1 | 0 | 0 | 3 | 9 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 2 | 4 | 0 | 0 | 0 | 0 |
| 1 | 1 | 5 | 17 | 5 | 7 | 29 | 85 | 6 | 10 | 116 | 1308 |
| 1 |
| 25 |
| 25 |
| 841 |
| 36 |
| 13456 |
|
|
Таблица 3
Уравнение регрессии
| Регрессионная статистика |
|
|
|
|
|
|
| ||
| Множественный R | 1,0000 |
|
|
|
|
|
|
| |
| R-квадрат | 0,9999 |
|
|
|
|
|
|
| |
| Нормированный R-квадрат | 0,9986 |
|
|
|
|
|
|
| |
| Стандартная ошибка | 1,2381 |
|
|
|
|
|
|
| |
| Наблюдения | 18,0000 |
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
| Дисперсионный анализ |
|
|
|
|
|
|
| ||
| df | SS | MS | F | Значимость F |
|
|
| ||
| Регрессия | 16,0000 | 19025,4116 | 1189,0882 | 775,7397 | 0,0282 |
|
|
| |
| Остаток | 1,0000 | 1,5328 | 1,5328 |
|
|
|
|
| |
| Итого | 17,0000 | 19026,9444 |
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | Нижние 95,0% | Верхние 95,0% | ||
| Y-пересечение | 3,3899 | 1,2355 | 2,7438 | 0,2225 | -12,3082 | 19,0880 | -12,3082 | 19,0880 | |
| Переменная X 1 | 3,0362 | 2,2817 | 1,3307 | 0,4103 | -25,9556 | 32,0281 | -25,9556 | 32,0281 | |
| Переменная X 2 | -0,0108 | 0,5682 | -0,0190 | 0,9879 | -7,2301 | 7,2085 | -7,2301 | 7,2085 | |
| Переменная X 3 | -3,7172 | 3,5010 | -1,0618 | 0,4809 | -48,2011 | 40,7668 | -48,2011 | 40,7668 | |
| Переменная X 4 | -2,6443 | 9,9430 | -0,2659 | 0,8345 | -128,9822 | 123,6936 | -128,982 | 123,693 | |
| Переменная X 5 | 0,5324 | 1,6637 | 0,3200 | 0,8028 | -20,6071 | 21,6719 | -20,6071 | 21,6719 | |
| Переменная X 6 | 1,2290 | 0,2498 | 4,9194 | 0,1277 | -1,9454 | 4,4035 | -1,9454 | 4,4035 | |
| Переменная X 7 | 4,4306 | 1,1278 | 3,9286 | 0,1587 | -9,8992 | 18,7604 | -9,8992 | 18,7604 | |
| Переменная X 8 | -1,3217 | 0,7883 | -1,6766 | 0,3424 | -11,3385 | 8,6951 | -11,3385 | 8,6951 | |
| Переменная X 9 | -7,1933 | 2,0811 | -3,4565 | 0,1793 | -33,6365 | 19,2498 | -33,6365 | 19,2498 | |
| Переменная X10 | 2,4789 | 2,8036 | 0,8842 | 0,5391 | -33,1441 | 38,1020 | -33,1441 | 38,1020 | |
| Переменная X11 | -6,2060 | 3,6940 | -1,6800 | 0,3418 | -53,1426 | 40,7307 | -53,1426 | 40,7307 | |
| Переменная X12 | 0,1895 | 0,9447 | 0,2006 | 0,8739 | -11,8139 | 12,1930 | -11,8139 | 12,1930 | |
| Продолжение таблицы 3 | |||||||||
| Переменная X13 | -3,0790 | 1,4643 | -2,1027 | 0,2826 | -21,6843 | 15,5263 | -21,6843 | 15,5263 | |
| Переменная X14 | 3,6276 | 0,9577 | 3,7876 | 0,1643 | -8,5418 | 15,7969 | -8,5418 | 15,7969 | |
| Переменная X15 | 0,8922 | 2,2192 | 0,4020 | 0,7566 | -27,3053 | 29,0897 | -27,3053 | 29,0897 | |
| Переменная X16 | 1,0370 | 0,2471 | 4,1974 | 0,1489 | -2,1022 | 4,1763 | -2,1022 | 4,1763 | |
Таблица 4
Оценка характера связи
| № | f(x1,x2) | yi-f | (yi-f)² | yi-y | (yi-y)² |
| 1 | 7,08524 | -0,08524 | 0,00727 | -35,05556 | 1228,89198 |
| 2 | 2,57699 | 0,42301 | 0,17894 | -39,05556 | 1525,33642 |
| 3 | 2,91742 | 0,08258 | 0,00682 | -39,05556 | 1525,33642 |
| 4 | 7,53805 | 0,46195 | 0,21339 | -34,05556 | 1159,78086 |
| 5 | 15,33512 | -0,33512 | 0,11230 | -27,05556 | 732,00309 |
| 6 | 29,00000 | 0,00000 | 0,00000 | -13,05556 | 170,44753 |
| 7 | 20,00000 | 0,00000 | 0,00000 | -22,05556 | 486,44753 |
| 8 | 38,19841 | -0,19841 | 0,03937 | -4,05556 | 16,44753 |
| 9 | 50,01632 | -0,01632 | 0,00027 | 7,94444 | 63,11420 |
| 10 | 79,00000 | 0,00000 | 0,00000 | 36,94444 | 1364,89198 |
| 11 | 109,88417 | 0,11583 | 0,01342 | 67,94444 | 4616,44753 |
| 12 | 87,61950 | 0,38050 | 0,14478 | 45,94444 | 2110,89198 |
| 13 | 54,56259 | -0,56259 | 0,31650 | 11,94444 | 142,66975 |
| 14 | 97,98368 | 0,01632 | 0,00027 | 55,94444 | 3129,78086 |
| 15 | 56,35546 | -0,35546 | 0,12635 | 13,94444 | 194,44753 |
| 16 | 33,80159 | 0,19841 | 0,03937 | -8,05556 | 64,89198 |
| 17 | 44,65904 | 0,34096 | 0,11625 | 2,94444 | 8,66975 |
| 18 | 20,46642 | -0,46642 | 0,21755 | -22,05556 | 486,44753 |
| ∑ | — | — | 1,53284 | — | 19026,94444 |
Содержание
Введение
1. Теоретическая часть
1.1. Однофакторный дисперсионный анализ
1.2. Линейный множественный регрессионный анализ
1.3. Множественный корреляционный анализ
2. Аналитическая часть
2.1. Сбор и первичная обработка данных
2.2. Дисперсионный анализ
2.3. Построение уравнения множественной регрессии
2.4. Исключение незначимых факторов
3. Заключение
4. Список литературы
5. Приложение
Введение
Анализируя данные, о смертности населения за 2004-2006 год, полученные в Нерюнгринской городской больнице (см. таблицу 1), можно сделать вывод о том, что общий коэффициент смертности, то есть число умерших от всех причин на 1000 человек населения, увеличивается (рис.1).
Показатель смертности на 1000 человек населения
Таблица 1
| 2004 год | 2005 год | 2006 год |
| 7.3 | 7.8 | 8.1 |
Рисунок 1
Несмотря на повышение рождаемости, демографическая ситуация в Нерюнгринском улусе характеризуется уменьшением численности населения. Главной причиной демографического кризиса является преобладание смертности над рождаемостью. Именно поэтому, чтобы снизить показатель смертности необходимо более детально изучить все причины и факторы, приводящие к ее увеличению. Несомненно, в изучении причин, важно исследование значимости отдельных нозологических форм заболеваний. Зная, какие заболевания приводят чаще всего к летальному исходу, можно разработать программу профилактических работ направленную на уменьшение числа данных заболеваний и предотвращения их дальнейшего развития на раннем этапе.
Цель: определение видов заболеваний оказывающих наибольшее влияние на показатели летальности, основываясь на статистике смертности населения Нерюнгринского улуса по классам болезней и возрастам за 2006 год.
Задачи:
1. сбор статистических данных необходимых для определения закономерности изменения смертности по причинам заболеваний;
2. проведение однофакторного дисперсионного анализа, с целью определения влияния различных болезней на общее количество смертности населения;
3. исключение отдельных факторов, оказывающих незначительное влияние;
4. построение уравнения множественной регрессии, отражающего соотношение между смертностью и различными классами заболеваний.
Теоретическая часть
Однофакторный дисперсионный анализ
Дисперсионный анализ (от латинского Dispersio - рассеивание) - статистический метод, позволяющий анализировать влияние различных факторов на исследуемую переменную. Метод был разработан биологом Р. Фишером в 1925 году и применялся первоначально для оценки экспериментов в растениеводстве. В дальнейшем выяснилась общенаучная значимость дисперсионного анализа для экспериментов в психологии, педагогике, медицине и др.
Целью дисперсионного анализа является проверка значимости различия между средними с помощью сравнения дисперсий. Дисперсию измеряемого признака разлагают на независимые слагаемые, каждое из которых характеризует влияние того или иного фактора или их взаимодействия. Последующее сравнение таких слагаемых позволяет оценить значимость каждого изучаемого фактора, а также их комбинации.
Пусть генеральные совокупности Х1, Х2,…, Хр распределены нормально и имеют одинаковую, хотя и неизвестную дисперсию. Математические ожидания которых известны и могут быть различны при заданном уровне значимости α. Проверим при заданном уровне значимости нулевую гипотезу Н0: М(Х1) = М(Х2) = … = М(Хр) о равенстве всех математических ожиданий. Это означает, что мы устанавливаем значимо или нет, различаются выборочные средние.
На практике дисперсионный анализ применяют, чтобы установить оказывает ли существенное влияние качественный фактор F, имеющий p уровней: F1, F2, …, Fp , на изучаемую величину.
Основная идея дисперсионного анализа состоит в сравнение «факторной дисперсии», то есть рассеяние, порождаемое изменением уровня фактора, и «остаточной дисперсии», обусловленной случайными причинами. Если их различие значимо, то фактор существенно влияет на Х и при изменении его уровня групповые средние различаются значимо. Если установили, что фактор существенно влияет на Х, а требуется выяснить, какой из уровней оказывает наибольшее воздействие, то дополнительно производим попарное сравнение средних. Дисперсионный анализ также применяется для установления однородности нескольких совокупностей (если математические ожидания одинаковы, то совокупности однородны). В более сложных случаях исследуют воздействие нескольких факторов на различные постоянные или различные уровни и выясняют влияние отдельных уровней и их комбинацию (многоуровневый анализ).
Будем считать, что количество наблюдений на каждом уровне фактора одинаково и равно q. Оформим результаты наблюдений в виде таблицы:
| Номер испытания | Уровни фактора Fj | |||
| F1 | F2 | … | Fp | |
| 1 2 … q | x11 x21 … xq1 | x12 x22 … xq2 | … … … … | x1p x2p … xqp |
| Групповое среднее |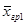 
| 
| … | 
|
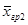
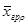
Сумму квадратов отклонения можно определить по формулам:
1. Общая сумма квадратов отклонений наблюдаемых значений от общего среднего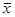 
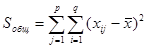[1]:
. (1)
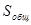характеризует влияние фактора F и случайных причин на Х.
2. Факторная сумма отклонений групповых средних от общей средней, характеризующая рассеяние между группами [1]:
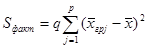. (2)
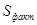характеризует воздействие фактора F на величину Х.
Остаточная сумма квадратов отклонений наблюдаемых значений группы от своего группового среднего, характеризующая рассеяние внутри групп [1]:
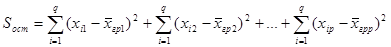. (3)
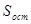отображает влияние случайных причин на Х.
Вводя обозначения [1]:
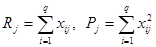, (4)
получим формулы, более удобные для расчетов [1]:
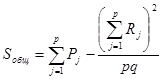, (5)
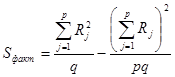. (6)
Разделив суммы квадратов на соответствующее число степеней свободы, получим общую, факторную и остаточную дисперсии [1]:
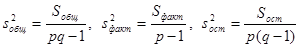. (7)
Если справедлива гипотеза Н0, то все эти дисперсии являются несмещенными оценками генеральной дисперсии.
Вычисляем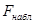 
и сравниваем с Fкр (критерий Фишера - Снедекора) [1]:
Fкр (α; n-1; nk-(k-1)),
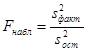, (8)
где α – уровень значимости; n – количество факторов; k – количество испытаний.
Если Fнабл < Fкр, то гипотеза о равенстве дисперсий будет принята.
Если число испытаний на разных уровнях различно (q1 испытаний на уровне F 1, q 2 – на уровне F 2 , …, qр - на уровне F р ), то [1]:
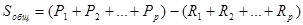, (9)
где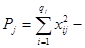 
сумма квадратов наблюдавшихся значений признака на уровне Fj,
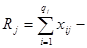сумма наблюдавшихся значений признака на уровне Fj .
При этом объем выборки, или общее число испытаний, равен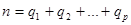 
. Факторная сумма квадратов отклонений вычисляется по формуле [1]:
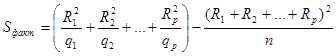. (10)
Остальные вычисления проводятся так же, как в случае одинакового числа испытаний [1]:
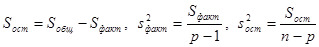. (11)
Дата: 2019-07-31, просмотров: 170.
