Динамические структуры данных, как поясняет Юрген Плате в следующих параграфах, изменяют свою структуру и занятое ими пространство памяти во время выполнения программы. Они формируются из отдельных элементов, так называемых 'узлов', между которыми существуют определенные взаимосвязи. Речь в основном при этом идет о структурах, которые обозначаются как 'списки' или 'деревья'.
Отношение отдельных узлов выстраиваются следующим образом: указатель одного узла указывает на место памяти «соседа». Самыми важными из этих структур данных являются:
· Линейные списки - простые цепочные списки, двойные цепочные списки, специальные формы, буфер(FIFO), стек(LIFO).
· Деревья - Бинарные деревья – 2 соседа, многодорожные деревья - больше чем 2 соседа.
· Общие графы
Линейные списки используют элементы, в которых указаны связанные сведения в форме строки символов. Элементы списков можно представить наглядно следующим образом:
| Информация элементов списка (строки символов, например, имя) | Указатель на следующий элемент |
При построении цепочного списка отдельные элементы списка выстраиваются в определенном порядке друг за другом:

где символ электрической массы в конце списка указывает на NULL-указатель, который показывает конец списка, а root - указатель, показывающий происхождение списка (как правило, глобальная переменная)
Еще одна важная динамическая структура, о которой рассказывает автор в этой главе – древовидная. Древовидные структуры играют очень важную роль в организации данных. Их используют в следующих случаях:
· при построении родословного дерева; · как организационная структура предприятия · при распределении текста по главам, разделам, абзацам и т.д.Дерево определяется следующим образом:
· Древовидные структуры имеют разветвления, которые могут исходить из начального элемента структуры и из самих разветвлений до тех пор, пока конечных точек не достигнут. · Элементы дерева называют узлами, причем начальный элемент называется корневым узлом, а конечные точки – листами. · Линии соединения двух узлов называется ребрами. Последовательность ребер от корня до любого узла называется путем. · Узлы, которые одинаково удалены от корня образуют уровень дерева. Общее число уровней указывает глубину дерева. · Максимальное количество наследников, которые имеет узел, определяют степень дерева. Дерево степени 2 - это бинарное дерево, наиболее важный случай.Древовидная структура имеет рекурсивную природу, так как наследники узла соответственно могут пониматься как корни деревьев. Бинарное дерево можно изобразить следующим образом:
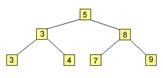
Таким образом, динамические структуры данных, как показывает автор, являются наиболее эффективным способом распределения оперативной памяти и соответственно необходимо их использовать в программе, применяя указатели.
Избранные алгоритмы
В этой главе Юрген Плате рассматривает наиболее распространенные и типичные виды алгоритмов, реализованные на Си.
· Обработка строк символов(Strings)
К простым операторам строк, которые задаются с помощью <ctype.h>, автор относит следующие операторы:
| islower(c) | Строчная буква |
| isupper(c) | Прописная буква |
| isalpha(c) | Строчная или прописная буква |
| isdigit(c) | Десятичное число |
| isalnum(c) | Строчная или прописная буква или десятичное число |
Наряду с простыми операторами имеется ряд комплексных команд для строковых символов. Прототипы находятся в стандартной библиотеке <STRING.H>.
· strcat (char *a, char *b) – Последовательность символов b прибавляется к a.
· strncat ( char *a , char *b , int n ) – прибавляются к а n символов b.
· strcpy ( char *a , char *b ) – строка b копируется после a
· strncpy ( char *a , char *b , int n ) – n символов строки b копируется после a
· int n = strlen ( char *a ) – возвращает длину строки
· Арифметика дат
В этом параграфе автором собраны достаточно простые алгоритмы, связанные с использованием даты и времени.
В первую очередь автор рассказывает о юлианском датоисчислении. При этом не имелось бы никакой проблемы 2000 года. Вместо этого дата сохранялась в компьютерах как строка символов (TTMMJJ) и это привело к тому, чтобы после 99 шел год 00. Причина такого датоисчисления была связана с необходимостью экономии памяти.
Алгоритм расчета даты по Юлианскому стилю можно представить следующим образом:
Y = год, М = месяц, D = день
Если M> 2, то Y и М остаются неизменными. Если М = 1 или М = 2, то
Y = Y - 1
М = М + 13
Для нахождения текущей даты имеем:
JD = INT (365 .25 * (Y + 4 716)) + INT (3 0.6001 * (М + 1)) + D + B - 1524.5
· Числовой тип
Здесь профессор приводит некоторые алгоритмы, которые работают с числовыми данными.
Достаточно часто в алгоритмах необходимо определить является ли число простым. Чтобы это устанавить, необходимо делить число X на числами, которые больше 2 и меньше X. Если число ни на какое из них не делится, оно должно быть простым.
Затем автор рассказывает о нахождении нулей функций. Для этого применяют методы аппроксимации. Если задан интервал (a;b), на котором определена функция, то необходимо каждый раз делить интервал пополам и проверять где находится нуль. Повторяется действие до тех пор, пока интервал не станет достаточно мал.
Еще один типичный пример рассмотрен в этом параграфе автором – решение систем линейных уравнений методом Гаусса.
Пусть задана система уравнений вида Ax = b. Считается, что если k-е уравнение будет решено, то:
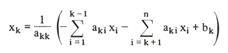
При решении методом Гаусса исходные уравнения преобразуют таким образом, что матрица коэффициентов содержит нули ниже главных диагоналей. Для этого используются операции сложения и вычитания уравнений, а также умножения их на число. При этом система принимает вид:
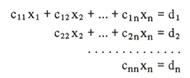
· Статистическая мера
В этом параграфе автор затрагивает статистический метод обработки информации и построение программ на основе этого метода. Статистика обрабатывает эмпирические числа и на основании этой обработки делаются прогнозы и принимаются решения.

Методом математической статистики анализируют массовые явления. При этом обнаруживаются определенные закономерности, которые нельзя формулировать для единичных явлений. Лучшим представлением статистических данных является графическое изображение. В качестве примера изображено распределение частоты гауссового нормального распределения.
Наряду с функцией частоты основную совокупность данных можно охарактеризовать с помощью среднего значения и дисперсии. Арифметическое среднее значение определяется так:
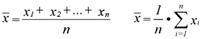
а дисперсия следующим образом:
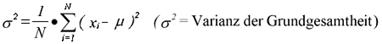
При работе с измерительными величинами часто необходимо установить связь между отдельными точками. Здесь помогают такие операции как интерполяция и регрессия.

При линейной интерполяции выполняют аппроксимацию функциональных значений f (x) на промежутке (x1,x2) из известных значений f (x1) и f (x2).

Поиск и сортировка
В этом параграфе автор рассказывает о наиболее распространенных в программировании операций с данными – поиске и сортировке.
Сортировка значительно облегчает работы с данными в программировании. Следствием таких операций является более эффективный поиск в программе.
Различают несколько основных методов поиска, зависящих от типа данных:
1. Табличный поиск осуществляется по индексу данных в таблице.
2. Линейный поиск предполагает просмотр всех элементов по порядку до нахождения нужного.
3. Бинарный поиск осуществляется после проведения сортировки, суть которого состоит в проверке среднего элемента последовательности и определения по ключу в какую сторону двигаться для нахождения нужного элемента.
Сортировка является одной из самых важных операций с данными. Профессор приводит такое определение сортировки:
Сортировка - процесс упорядочения заданного множества объектов в определенном порядке. Выделяют следующие виды алгоритмов сортировки:
§ Пузырьковая сортировка. В первом проходе массив обрабатывается с конца до начала и сравнивается при каждом шаге текущий компонент со следующим. Если нижний компонент меньше чем верхний, то они меняются местами. Это происходит до тех пор, пока последовательность не будет возрастающей или убывающей.
§ Сортировка выбором. В этом случае берут первый элемент последовательности и ищут самый маленький элемент, с которым его и меняют местами. Затем начинают со второго и его меняют на самый маленький в оставшейся последовательности и т.д.
§ Сортировка вставкой. При этом предполагается, что часть последовательности уже отсортирована. Элементы не сортированной части по порядку перемещают в сортированную до тех пор пока элемент не станет больше или равным впереди идущего элемента.
§ Сортировка методом Шелла. Сначала массив разделяется на несколько групп, между членами которых имеется равное расстояние. Пусть, например, используется расстояние 3, тогда компоненты 1, 4, 7 принадлежат одной группе, так же как и 2, 5, 8..., 3, 6, 9... и т.д. эти группы упорядочиваются в отдельности, затем расстояние уменьшается и действия повторяется до расстояния 1.
§ Быстрая сортировка. Выбирают любой компонент массива - к примеру, средний - и массив делится на 2 группы: одна с компонентами, которые больше чем выбранный, а другая с меньшими. Эти обе группы делятся вновь по заданному алгоритму. Таким образом, получается рекурсивная функция, которая достаточно быстро сортирует данные.
· Реализация множеств
Автор в этой главе упоминает о множествах – достаточно важной структуре программирования. Другие языки программирования (например, Паскаль) имеют тип данных множества. В языке C такого не имеется.
Однако множества возможно представить с помощью битовых массивов. Элементы массива нумеруются, и каждый элемент множества представляет собой 1 бит. Если соответствующий бит установлен (1), то элемент содержится в множестве, если бит равен 0, соответствующий элемент не содержится в множестве. Пересечение и объединение можно использовать с помощью логических операторов UND и ODER. Так как переменные величины типа int или char только относительно маленькие множества могут представлять, то получить к ним доступ можно с помощью указателя на битовый массив.
Дата: 2019-07-31, просмотров: 268.