Результаты, полученные на основе модели бесконечных периодических структур, позволяют оценить свойства центральных излучателей больших АР. Часто требуется выполнить расчеты для АР малых размеров, либо исследовать краевые эффекты в больших АР. Расчет взаимных сопротивлений можно выполнять и методами поэлементного подхода, но как правило это сложная электродинамическая задача. Решить данную задачу позволяет процедура, построенная на основе эквивалентности метода поэлементного расчета входных сопротивлений излучателя в бесконечной АР и метода, основанного на теории бесконечных периодических структур [2].

Входное сопротивление элемента бесконечной периодической линейной решетки

Для линейной решетки полосковых вибраторов, расположенных на многослойной диэлектрической подлжке (рис. 2.1) и имеющих распределение тока

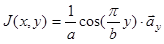, (2.1)

где 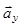-единичный вектор, входное сопротивление можно записать в виде [1]

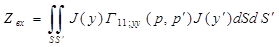, (2.2)

где J(y) – распределение тока по (2.1);

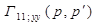- скалярная компонента функции Грина при разложении полей по волнам Е и Н.

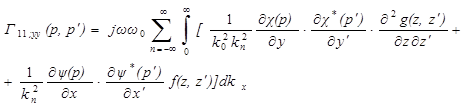, (2.3)

где 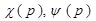- собственные функции [1];

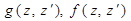-характеристические части функции Грина.

Записав выражения для характеристических частей и собственных функций и подставив их в (2.2) и (2.3), получим выражение для расчета входного сопротивления вибратора, имеющего структуру как на рис. 2.1 и находящегося в составе бесконечной решетки с периодом B [1]

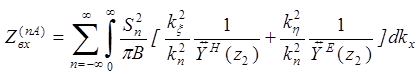, (2.4)

где B=nA – период решетки;

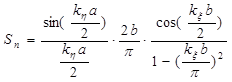- множитель, учитывающий распределение тока по вибратору;

;

;

;

;

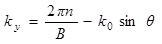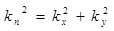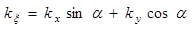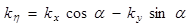α – угол наклона излучателей в решетке (α=0° – параллельные излучатели, α=90° – коллинеарные излучатели).

Для слоистой структуры, представленной на рис. 2.1, проводимость в сечении 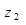 определяется по следующим рекурентным формулам:

;

;

;

;

; ;

; ; .

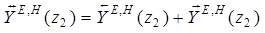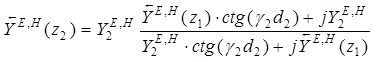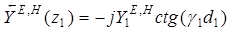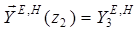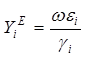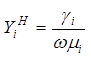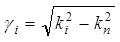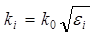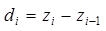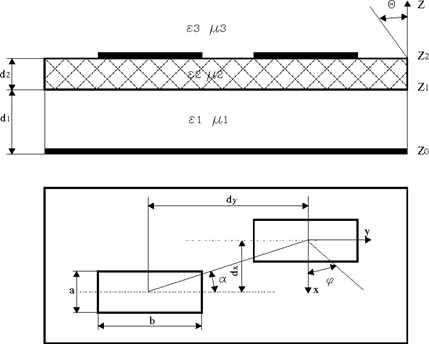
Рис. 2.1 Геометрия полосковых излучателей на многослойной диэлектрической подложке

Выражение для расчета входного сопротивления вибратора, имеющего структуру как на рис. 2.2и находящегося в составе бесконечной решетки с периодом B имеет следующий вид [1]

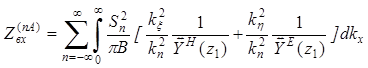, (2.5)

Для слоистой структуры, представленной на рис. 2.2, проводимость в сечении 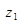 определяется по следующим рекурентным формулам:

;

;

;

;

; ;

; ; .

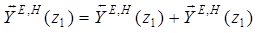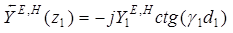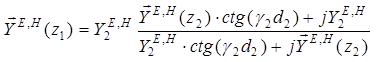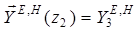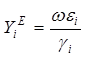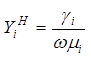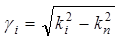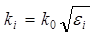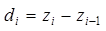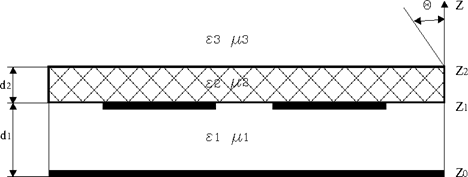
Рис. 2.2 Полосковые излучатели на перевернутой диэлектрической подложке

Разложение функции Грина по волнам Е и Н, используемые в данном случае, позволяет получить компактную и достаточно простую запись выражений для расчета входного сопротивления элемента, находящегося в составе бесконечной периодической линейной решетки.