В уравнениях нормальной системы (1.10)
| 
| 
| 
| 
| 
|
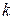
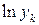
| 1 | -1,5 | 6,50 | 2,25 | 1,8718 | -2,8077 |
| 2 | -1,2 | 4,30 | 1,44 | 1,4586 | -1,7503 |
| 3 | -0,9 | 3,53 | 0,81 | 1,2613 | -1,1352 |
| 4 | -0,6 | 2,93 | 0,36 | 1,0750 | -0,6450 |
| 5 | -0,3 | 2,42 | 0,09 | 0,8838 | -0,2651 |
| 6 | 0,0 | 2,01 | 0,00 | 0,6981 | 0,0000 |
| 7 | 0,3 | 0,68 | 0,09 | -0,3857 | -0,1157 |
| 8 | 0,6 | 1,67 | 0,36 | 0,5128 | 0,3077 |
| 9 | 0,9 | 0,03 | 0,81 | -3,5066 | -3,1559 |
| 10 | 1,2 | 0,57 | 1,44 | -0,5621 | -0,6745 |
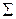
| -1,50 | 24,64 | 7,65 | 3,3071 | -10,2418 |
Подставляя результаты суммирования из табл. 1.6, получаем систему двух линейных алгебраических уравнений:
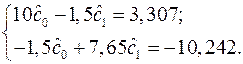
Решая эту систему по формулам (1.11), получаем: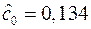 
, 
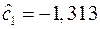. Отсюда оценки параметров экспоненциальной зависимости: 
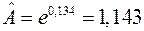и 
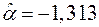. Таким образом, среднеквадратичное приближение данных, представленных в табл. 1.2, имеет вид
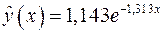. (1.12)
Для оценки степени адекватности (погрешности среднеквадратичного приближения) построенной математической модели (1.12) данным из табл. 1.2 найдем значения экспоненциальной зависимости в узлах этой таблицы.
Таблица 1.7
Данные для оценки адекватности экспоненциальной зависимости (1.12)
Таблично заданной функции
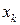
| -1,5 | -1,2 | -0,9 | -0,6 | -0,3 | 0,0 | 0,3 | 0,6 | 0,9 | 1,2 |
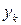
| 6,500 | 4,300 | 3,530 | 2,930 | 2,420 | 2,010 | 0,680 | 1,670 | 0,030 | 0,570 |
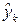
| 8,188 | 5,523 | 3,725 | 2,513 | 1,695 | 1,143 | 0,771 | 0,520 | 0,351 | 0,237 |
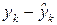
| -1,688 | -1,223 | -0,195 | 0,417 | 0,725 | 0,867 | -0,091 | 1,150 | -0,321 | 0,333 |
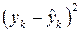
| 2,849 | 1,495 | 0,038 | 0,174 | 0,526 | 0,751 | 0,008 | 1,322 | 0,103 | 0,111 |
Из данных, представленных в табл. 1.7, следует, что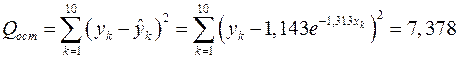 
и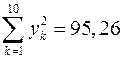 
.
Отсюда погрешность среднеквадратичного приближения составляет
.
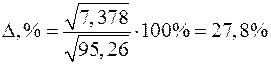Очевидно, что остаточная сумма квадратов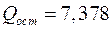 
в данном случае существенно превышает величину 
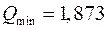. Это связано с тем, что при формировании системы нормальных уравнений минимизировалась не величина 
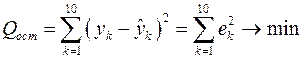, как это требуется в соответствии с принципом Лагранжа, а квадрат “невязки”, то есть величина 
.
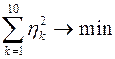Чтобы устранить этот серьёзный недостаток, продолжим дальнейшие преобразования модели (1.9):
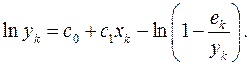(1.13)
Так как при малых значениях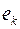 
: 
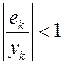имеет место разложение 
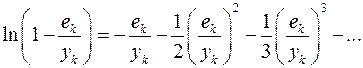, выражение (1.13) можно представить в ви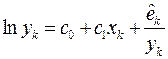де 
, где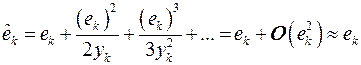 
.
Отсюда получаем:
; 
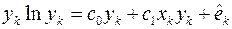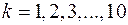. (1.14)
Оценки коэффициентов модели (1.14) находим из условия минимизации функционала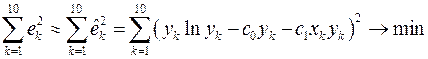 
.
Отсюда можно получить линейную систему нормальных уравнений вида
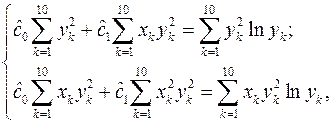(1.15)
коэффициенты которой вычисляются по формулам:
;
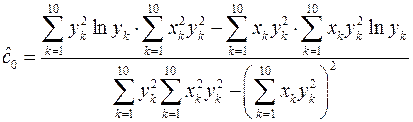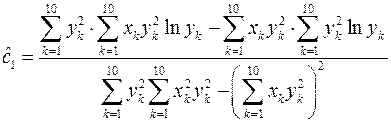. (1.16)
Для вычисления коэффициентов в системе уравнений (1.16) используем данные из табл. 1.2 и формируем табл. 1.8.
Таблица 1.8
Данные для вычисления коэффициентов в уравнениях
Нормальной системы (1.15)
|
| 
|
| 
| 
| 
| 
| 
|
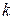
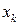
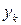
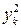
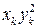
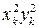
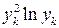
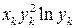
| 1 | -1,5 | 6,50 | 42,25 | -63,375 | 95,063 | 79,084 | -118,625 |
| 2 | -1,2 | 4,30 | 18,49 | -22,188 | 26,626 | 26,970 | -32,364 |
| 3 | -0,9 | 3,53 | 12,46 | -11,215 | 10,093 | 15,717 | -14,145 |
| 4 | -0,6 | 2,93 | 8,58 | -5,151 | 3,091 | 9,229 | -5,537 |
| 5 | -0,3 | 2,42 | 5,86 | -1,757 | 0,527 | 5,176 | -1,553 |
| 6 | 0,0 | 2,01 | 4,04 | 0,000 | 0,000 | 2,821 | 0,000 |
| 7 | 0,3 | 0,68 | 0,46 | 0,139 | 0,042 | -0,178 | -0,053 |
| 8 | 0,6 | 1,67 | 2,79 | 1,673 | 1,004 | 1,430 | 0,858 |
| 9 | 0,9 | 0,03 | 0,00 | 0,001 | 0,001 | -0,003 | -0,003 |
| 10 | 1,2 | 0,57 | 0,32 | 0,390 | 0,468 | -0,183 | -0,219 |
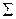
| -1,50 | 24,64 | 95,26 | -101,483 | 136,913 | 140,061 | -171,642 |
Подставляя результаты суммирования из табл. 1.8, получаем систему двух линейных алгебраических уравнений:
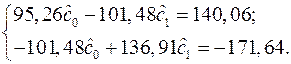
Решая эту систему по формулам (1.16), получаем: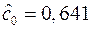 
, 
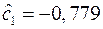. Отсюда оценки параметров экспоненциальной зависимост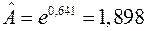и: 
и 
. Таким образом, среднеквадратичное приближение данных, представленных в табл. 1.2, имеет вид
. (1.17)
Для оценки степени адекватности (погрешности среднеквадратичного приближения) построенной модели данным из табл. 1.2 найдем значения экспоненциальной зависимости (1.17) в узлах этой таблицы.
Таблица 1.9
Данные для оценки адекватности
Экспоненциальной зависимости (1.17)
Таблично заданной функции
|
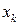
| -1,5 | -1,2 | -0,9 | -0,6 | -0,3 | 0,0 | 0,3 | 0,6 | 0,9 | 1,2 |
|
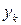
| 6,500 | 4,300 | 3,530 | 2,930 | 2,420 | 2,010 | 0,680 | 1,670 | 0,030 | 0,570 |
|
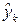
| 6,103 | 4,832 | 3,825 | 3,028 | 2,397 | 1,898 | 1,502 | 1,189 | 0,941 | 0,745 |
|
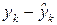
| 0,397 | -0,532 | -0,295 | -0,098 | 0,023 | 0,112 | -0,822 | 0,481 | -0,911 | -0,175 |
|
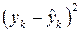
| 0,157 | 0,283 | 0,087 | 0,010 | 0,001 | 0,013 | 0,676 | 0,231 | 0,831 | 0,031 |
Из данных, представленных в табл. 1.9, следует, что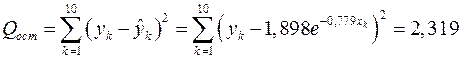 
и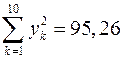 
.
Отсюда погрешность среднеквадратичного приближения
.
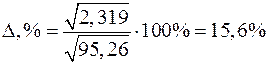Очевидно, что в данном случае остаточная сумма квадратов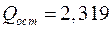 
почти в три раза меньше, чем для модели (1.12) и достаточно близка к минимальной величине .
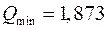На рис. 1.1 изображены точки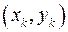 
, 
, из табл. 1.2 и построены два графика экспоненциальной зависимости: кривая 2 описывает зависимость (1.12), а кривая 3 – зависимость (1.17).
Пример 1.2. По данным из табл. 1.10, применяя метод наименьших квадратов, оценить параметры степенной зависимости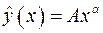 
.
Линеаризируя по параметрам заданную нелинейную зависимость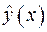 
, найти среднеквадратичные оценк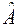и 
и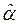 
.
Используя логарифмирование нелинейной зависимости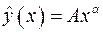 
, построить линейную модель, оценить методом наименьших квадратов её параметры и на основе этих оценок найти параметры заданной нелинейной зависимости.
Используя преобразование построенной посредством логарифмирования линейной модели, повысить степень адекватности функции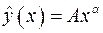 
табличным данным 
.
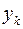Вычислить значения построенных зависимостей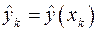 
в узлах таблицы и оценить погрешности среднеквадратичного приближения.
Таблица 1.10
Исходные данные для примера 1.2
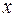
| 1,0 | 1,3 | 1,6 | 1,9 | 2,2 | 2,5 | 2,8 | 3,1 | 3,4 | 3,7 |
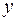
| 0,87 | 0,66 | 0,52 | 0,38 | 0,28 | 0,20 | 0,19 | 0,13 | 0,08 | 0,12 |
В соответствии с условием задачи для описания данных из табл. 1.10 используем степенную зависимость вида 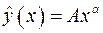, которая в узлах таблицы 
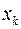принимает значения
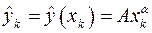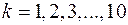, . (1.18)
Эти значения в силу различных причин могут отличаться от табличных данных 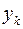на величины (остатки) 
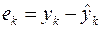, которые носят случайный характер.
Согласно методу наименьших квадратов оценки параметров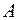 
и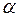 
должны вычисляться из условия минимизации функционала – суммы квадратов отклонения значений 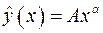степенной зависимости от табличных данных 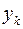, то есть суммы квадратов остатков (принцип Лежандра) [6]:
.
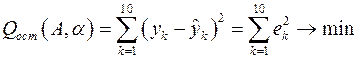В этом случае система нормальных уравнений формируется на основе вычисления частных производных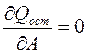 
и 
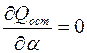. Нелинейность выбранной функциональной зависимости, описывающей табличные данные, приводит к нелинейности системы нормальных уравнений относительно параметров 
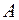и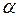 
, что существенно усложняет процедуру их вычисления [2,5].
Действительно, вычисляя частные производные от функционала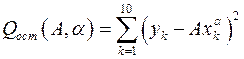 
и приравнивая их нулю, получаем:
$
.
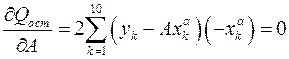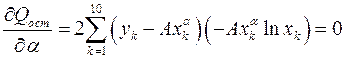Отсюда система нормальных уравнений принимает следующий вид:
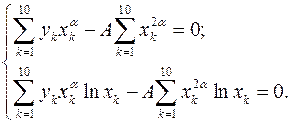(1.19)
При решении системы нелинейных уравнений (1.19) можно воспользоваться методом Ньютона [2, 3, 5]. Алгоритм вычислений на
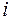-той итерации метода Ньютона, 
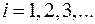, описывается рекуррентной формулой (1.4), где 
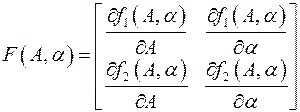– матрица Якоби; 
; 
;
; 
;
; 
.
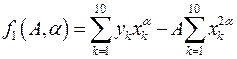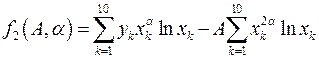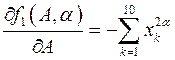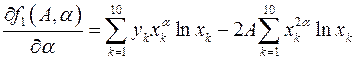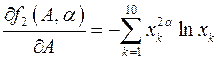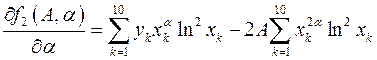Начальное приближение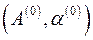 
можно выбрать, например, из условия прохождения степенной функции через первую и последнюю точки табл. 1.10: 
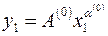и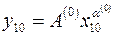 
. Отсюда легко получить соотношения:
; 
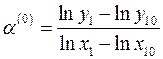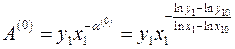. (1.20)
Подставляя данные из табл. 1.10, получаем начальное приближение для итерационной процедуры (1.4):
, 
.
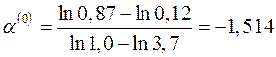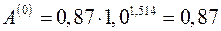На первом шаге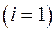 
итерационной процедуры находим:
;
;
, 
;
;
;
, 
,
,
, 
,
.
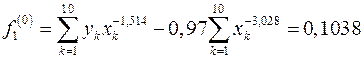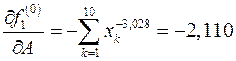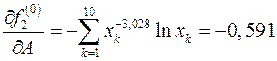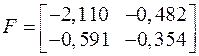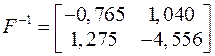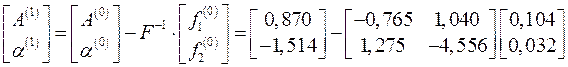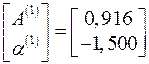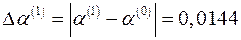Результаты вычислений на основе рекуррентной формулы (1.4) для последующих шагов представлены в табл. 1.11. Очевидно, что уже на третьей итерации изменение оценок параметров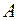 
и 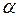по абсолютной величине не превосходит 0,001:
; 
.
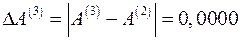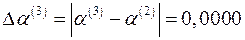Таблица 1.11
Дата: 2019-07-30, просмотров: 153.
