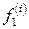
0	1,681	-0,901	-2,211	2,539	-35,61	68,130	39,01	-90,76
1	1,633	-0,894	-0,034	0,045	-35,05	62,53	38,26	-83,31	0,0481	0,0073
2	1,633	-0,894	0,000	0,000	-35,01	62,40	38,20	-83,12	0,0000	0,0005
3	1,633	-0,894	0,000	0,000	-35,01	62,40	38,20	-83,12	0,0000	0,0000

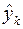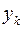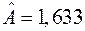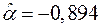Таким образом, минимум суммы квадратов отклонения значений  экспоненциальной зависимости от табличных данных  достигается при значениях её параметров  и  (с погрешностью, не превышающей 0,001). При этом остаточная сумма квадратов составляет

,

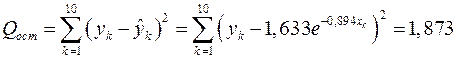что в относительных единицах равно 14,0 %.

Полученная величина 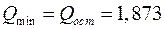 может служить критерием для сравнения с остаточной суммой квадратов, соответствующей какой-либо другой оценке параметров экспоненциальной зависимости, вычисленной тем или иным способом.

Рассматриваемая задача однофакторной нелинейной регрессии была сведена к решению нормальной системы нелинейных уравнений методом Ньютона. Другим известным подходом к решению задачи нелинейного оценивания является линейная параметризация математической модели [6].

Разложим функцию 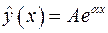 в ряд Тейлора в окрестности точки :

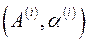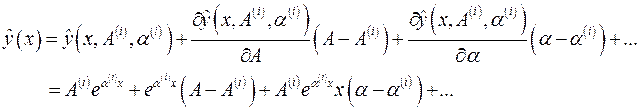
Ограничиваясь линейной частью разложения, получаем аппроксимацию:

,

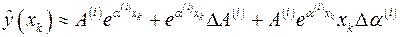где , .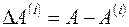

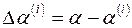В этом случае сумма квадратов остатков (1.2) будет описываться выражением вида

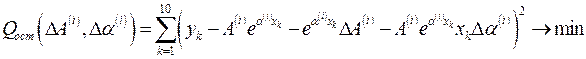. (1.6)

Очевидно, что функционал (1.6) представляет собой квадратичную форму относительно параметров 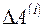 и 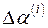 и, следовательно, система нормальных уравнени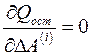й  и 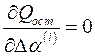 будет линейной относительно этих параметров:

;

.

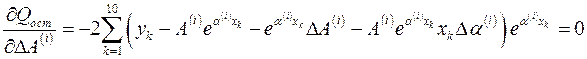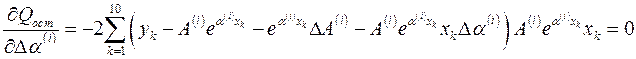Отсюда имеем:

;

.

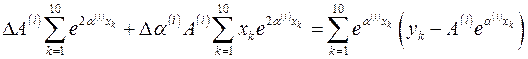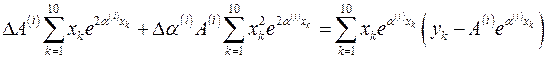Вводя обозначения 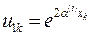, , 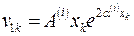, , 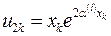, , 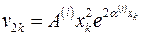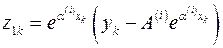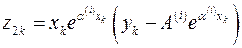получаем систему уравнений

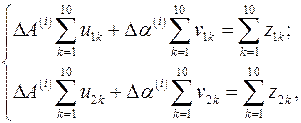                   (1.7)

из решения которой находим

, .

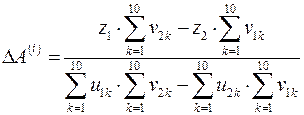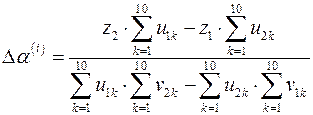Вычисляя новые приближения по формулам 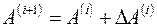 и 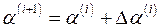, получаем итерационный процесс уточнения параметров заданной нелинейной зависимости,  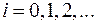– номер итерации. Условием завершения итерационной процедуры может служить выполнение неравенств: 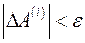, , 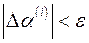где 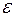 – заданная величина погрешности вычислений.

В качестве начального приближения 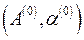 можно взять значения, полученные выше по формулам (1.5): , .

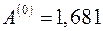Данные для вычисления коэффициентов нормальной системы уравнений (1.7) на первой итерации 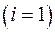 представлены в табл. 1.4.

Таблица 1.4

Данные для вычисления коэффициентов нормальной системы
уравнений (1.7) на первом шаге итерационной процедуры

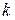
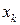
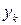
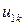
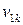
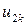
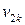
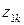
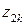
1	-1,5	6,50	14,924	-37,632	-22,387	56,448	0,023	-0,034
2	-1,2	4,30	8,692	-17,533	-10,430	21,040	-1,934	2,321
3	-0,9	3,53	5,062	-7,659	-4,556	6,893	-0,567	0,511
4	-0,6	2,93	2,948	-2,974	-1,769	1,784	0,075	-0,045
5	-0,3	2,42	1,717	-0,866	-0,515	0,260	0,285	-0,085
6	0,0	2,01	1,000	0,000	0,000	0,000	0,329	0,000
7	0,3	0,68	0,582	0,294	0,175	0,088	-0,460	-0,138
8	0,6	1,67	0,339	0,342	0,204	0,205	0,402	0,241
9	0,9	0,03	0,198	0,299	0,178	0,269	-0,319	-0,287
10	1,2	0,57	0,115	0,232	0,138	0,278	0,000	0,000
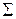
			35,578	-65,497	-38,963	87,266	-2,166	2,483

Система нормальных уравнений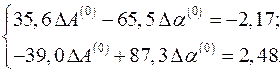

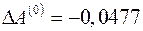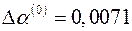имеет решение:  и . Отсюда новые уточненные оценки параметров:  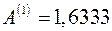и .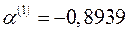

Данные для вычисления коэффициентов нормальной системы уравнений (1.7) на второй итерации 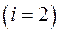 представлены в табл. 1.5.

Таблица 1.5

Данные для вычисления коэффициентов нормальной системы
уравнений (1.7) на втором шаге итерационной процедуры

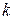
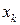
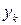
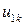
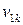
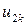
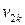
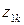
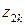
1	-1,5	6,50	14,608	-35,789	-21,912	53,683	0,984	-1,477
2	-1,2	4,30	8,544	-16,746	-10,253	20,095	-1,386	1,663
3	-0,9	3,53	4,998	-7,346	-4,498	6,611	-0,271	0,244
4	-0,6	2,93	2,923	-2,864	-1,754	1,719	0,235	-0,141
5	-0,3	2,42	1,710	-0,838	-0,513	0,251	0,372	-0,112

Окончание табл. 1.5

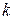
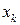
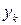
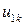
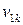
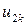
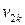
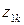
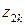
6	0,0	2,01	1,000	0,000	0,000	0,000	0,377	0,000
7	0,3	0,68	0,585	0,287	0,175	0,086	-0,435	-0,131
8	0,6	1,67	0,342	0,335	0,205	0,201	0,418	0,251
9	0,9	0,03	0,200	0,294	0,180	0,265	-0,313	-0,282
10	1,2	0,57	0,117	0,229	0,140	0,275	0,004	0,005
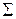
			35,027	-62,438	-38,229	83,187	-0,015	0,020

Система нормальных уравнений ;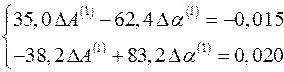

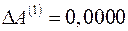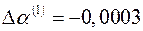имеет решение:  и . Отсюда новые, уточненные оценки параметров:  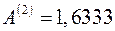и 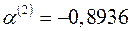. Так как  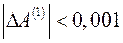и 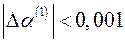, эти оценки с погрешностью, не превышающей 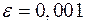, обеспечивают минимум остаточной суммы квадратов (1.6). Очевидно, что полученный результат  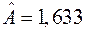и 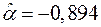 совпадает с результатом вычислений методом Ньютона, причем в обоих случаях потребовалось по две итерации. Следовательно, и остаточные суммы квадратов будут одинаковыми: .

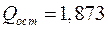Рассмотрим решение задачи из примера 1.1 на основе линеаризующих преобразований нелинейной зависимости посредством логарифмирования [2, 6]. Целью таких преобразований является сведение системы нормальных уравнений к линейному виду, что существенно упрощает её решение.

Представим табличные данные 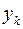 в виде

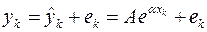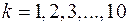, .      (1.8)

Прологарифмируем обе части выражения (1.8):

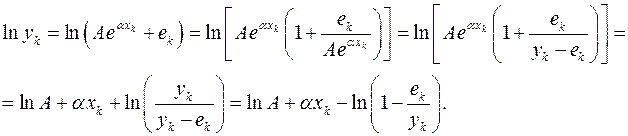
Обозначая 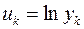, , 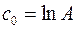  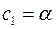и , получаем линейную по параметрам 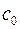 и 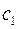 модель, описывающую табличные данные :

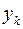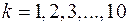,   .          (1.9)

Минимизируя квадрат “невязки”: 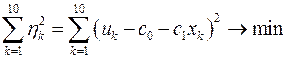, получаем линейную систему нормальных уравнений

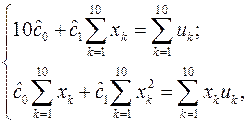                       (1.10)

коэффициенты которой вычисляются по формулам:

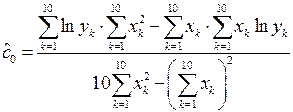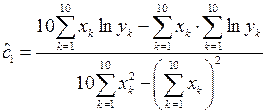; . (1.11)

С учетом введенных обозначений оценки параметров экспоненциальной зависимости находятся по формулам 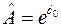 и .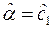

Для вычисления коэффициентов в системе уравнений (1.10) используем данные из табл. 1.2 и формируем табл. 1.6.

Таблица 1.6