Метод заключается в том, что строят графические зависимости LgR0=f(LgC0) или/и R0=f(C0) для опытов, где значения концентраций других компонентов, кроме исследуемого, одинаковы.
| Ro | Co1 | Co2 | LgRo | lgCo1 | lgCo2 | Ck | LgCk | |||||||
| 0,0056 | 6 | 0,3 | -2,251812 | 0,7781513 | -0,522878 | 0,1 | -1 | |||||||
| 0,0056 | 6 | 0,6 | -2,251812 | 0,7781513 | -0,221848 | 0,1 | -1 | |||||||
| 0,0051 | 6 | 0,9 | -2,292429 | 0,7781513 | -0,045757 | 0,1 | -1 | |||||||
| 0,0036 | 4 | 0,6 | -2,443697 | 0,60206 | -0,221848 | 0,1 | -1 | |||||||
| 0,0015 | 2 | 0,6 | -2,823908 | 0,30103 | -0,221848 | 0,1 | -1 | |||||||
| 0,0115 | 6 | 0,6 | -1,939302 | 0,7781513 | -0,221848 | 0,2 | -0,69897 | |||||||
| 0,0167 | 6 | 0,6 | -1,777283 | 0,7781513 | -0,221848 | 0,3 | -0,522878 | |||||||
|
Определение порядка реакции по компоненту А1-бензол. | ||||||||||||||
| Ro | Co1 | Co2 | Ck | LgRo | lgCo1 |
| ||||||||
| 0,0056 | 6 | 0,6 | 0,1 | -2,251812 | 0,7781513 |
| ||||||||
| 0,0036 | 4 | 0,6 | 0,1 | -2,4436975 | 0,60206 |
| ||||||||
| 0,0015 | 2 | 0,6 | 0,1 | -2,8239087 | 0,30103 |
| ||||||||
Зависимость LgR0=f(LgC01) Зависимость R0=f(C01)
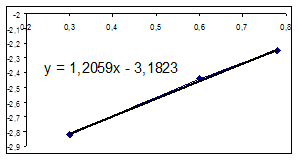
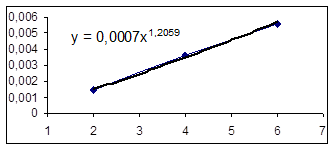
Порядок по компоненту А1 (бензолу) принимаем равным 1, т. к.1,2 примерно равно 1.
Определение порядка по катализатору.
| Ro | Co1 | Co2 | Ck | LgRo | LgCk |
| 0,0056 | 6 | 0,6 | 0,1 | -2, 207608 | -1 |
| 0,0115 | 6 | 0,6 | 0,2 | -1,879426 | -0,69897 |
| 0,0167 | 6 | 0,6 | 0,3 | -1,790485 | -0,522878 |
Зависимость R0=f(Ck) Зависимость LgR0=f(LgCk)
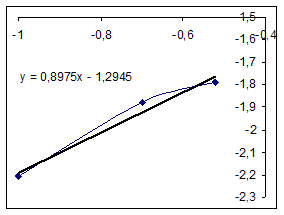
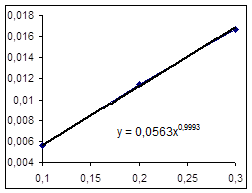 |
Порядок по катализатору примем равным 1.
Порядок по хлору определять не будем, т. к. его концентрацию поддерживают постоянной. Скорость реакции от него не будет зависеть.
Таким образом, вид кинетического уравнения для нашей реакции выглядит следующим образом:
R=kC1Ck∑
Определение вида кинетической модели интегральным методом
Уравнение реакции:
C6H6(A1) + Cl2(A2) = C6H6Cl(A3) + HCl(A4)
d [A3] /dt = r = k [A1] [A2] = - d [A1] /dt
Проинтегрируем по t: - ò d [A1] / [A1] = ò k [A2] dt
ln [A1] 0 – ln [A1] = k [A2] t, т. к. концентрация хлора (А2) постоянна, выносим ее за знак интеграла.
 |
Ln([A1] 0/ [A1]) = k [A2] t, обозначим k [A2] º Кнабл.
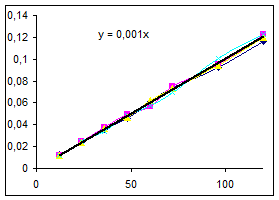
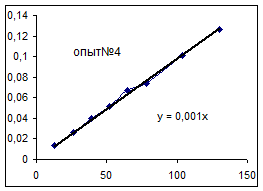
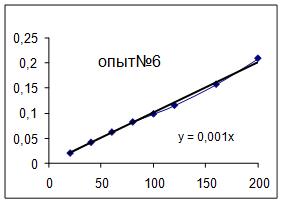
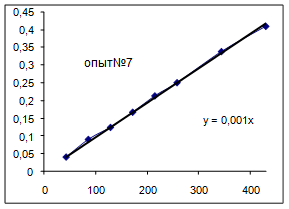
Определим графически значение Кнабл по всем опытам.
| №опыта | 1 | 2 | 3 | 5 |
| Т, мин | Ln(C01/C1) | Ln(C01/C1) | Ln(C01/C1) | Ln(C01/C1) |
| 12 | 0,0125788 | 0,0122413 | 0,012072581 | 0,0115666 |
| 24 | 0,0236099 | 0,0248051 | 0,023780529 | 0,0246343 |
| 36 | 0,0356272 | 0,0377019 | 0,036663984 | 0,0342464 |
| 48 | 0,0458694 | 0,0493653 | 0,046742263 | 0,0481404 |
| 60 | 0,0613436 | 0,0570996 | 0,062230077 | 0,0579823 |
| 72 | 0,0743644 | 0,0750828 | 0,07364654 | 0,0693501 |
| 96 | 0,0926637 | 0,0952268 | 0,094310679 | 0,1007416 |
| 120 | 0,115785 | 0,1225444 | 0,119534569 | 0,1221676 |
| №опыта | 4 |
| 6 |
| 7 |
| 8 |
| Т, мин | Ln(C01/C1) | Т, мин | Ln(C01/C1) | Т, мин | Ln(C01/C1) | Т, мин | Ln(C01/C1) |
| 13 | 0,0132541 | 20 | 0,020202707 | 43 | 0,040822 | 6 | 0,0122413 |
| 26 | 0,026344 | 40 | 0,04160355 | 86 | 0,0904719 | 12 | 0,0236099 |
| 39 | 0,0403013 | 60 | 0,061875404 | 129 | 0,1244301 | 18 | 0,0373558 |
| 52 | 0,0514687 | 80 | 0,082023835 | 172 | 0,1672359 | 24 | 0,0486652 |
| 65 | 0,0672087 | 100 | 0,098164249 | 215 | 0,2131932 | 30 | 0,060635 |
| 78 | 0,0740054 | 120 | 0,115130307 | 258 | 0,2503863 | 36 | 0,073826 |
| 104 | 0,1007416 | 160 | 0,15694625 | 344 | 0,3382739 | 48 | 0,1007416 |
| 130 | 0,1265085 | 200 | 0, 208562868 | 430 | 0,4094731 | 60 | 0,1210383 |
| №опыта | 9 |
| Т, мин | Ln(C01/C1) |
| 4 | 0,0122413 |
| 8 | 0,0239512 |
| 12 | 0,0345914 |
| 16 | 0,0483153 |
| 20 | 0,0616981 |
| 24 | 0,0723915 |
| 32 | 0,0955936 |
| 40 | 0,1184082 |
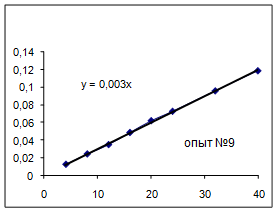
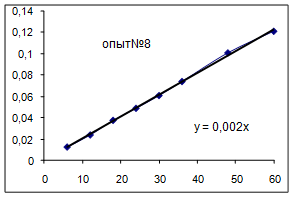
Как видно из уравнений прямых на диаграммах, значение Кнабл для всех опытов, кроме последних двух, одинаково и равно 0,001. Значит, в последних двух опытах действует какой-то другой параметр системы. Причем явно видно, что от концентрации хлора Кнабл совсем не зависит, т. к. для всех первых 7 опытов значение константы одинаково, но значение начальной концентрации хлора разное.
Если предположить, что в кинетическом уравнении вместо [A2] стоит суммарная концентрация катализатора, то тенденция в изменении Кнабл выглядит закономерной:
| Кнабл | Ск |
| 0,001 | 0,1 |
| 0,002 | 0,2 |
| 0,003 | 0,3 |
Определение значения константы скорости методом наименьших квадратов
Метод заключается в следующем:
R = k•C1•Ck∑
можно представить в виде уравнения прямой: у = Вх, где y=R, B=k, x=C1•Ck∑.
Домножая правую и левую часть уравнения у = Вх на х, получим квадратичное уравнение ух = Вх2.
Значение константы вычислим как: В = ух / х2.
№опыта
| 1 | 2 | 3 | 5 | 4 | 6 | 7 | 8 | 9 | |||||||
| R | R | R | R | R | R | R | R | R | |||||||
| 0,0056 | 0,0056 | 0,0056 | 0,0056 | 0,0051 | 0,0036 | 0,0015 | 0,0115 | 0,0167 | |||||||
| С1•Сk | С1•Сk | С1•Сk | С1•Сk | С1•Сk | С1•Сk | С1•Сk | С1•Сk | С1•Сk | |||||||
| 0,5925 | 0,5927 | 0,5928 | 0,5931 | 0,5921 | 0,392 | 0, 192 | 1,1854 | 1,7781 | |||||||
| (С1•Сk) 2 | (С1•Сk) 2 | (С1•Сk) 2 | (С1•Сk) 2 | (С1•Сk) 2 | (С1•Сk) 2 | (С1•Сk) 2 | (С1•Сk) 2 | (С1•Сk) 2 | |||||||
| 0,351056 | 0,351293 | 0,351412 | 0,351768 | 0,350582 | 0,153664 | 0,036864 | 1,405173 | 3,16164 | |||||||
| R•C1•Ck | R•C1•Ck | R•C1•Ck | R•C1•Ck | R•C1•Ck | R•C1•Ck | R•C1•Ck | R•C1•Ck | R•C1•Ck | |||||||
| 0,003318 | 0,003319 | 0,00332 | 0,003321 | 0,00302 | 0,001411 | 0,000288 | 0,013632 | 0,029694 | |||||||
| B=YX/X2 | B=YX/X2 | B=YX/X2 | B=YX/X2 | B=YX/X2 | B=YX/X2 | B=YX/X2 | B=YX/X2 | B=YX/X2 | |||||||
| 0,009451 | 0,009448 | 0,009447 | 0,009442 | 0,008613 | 0,009184 | 0,007813 | 0,009701 | 0,009392 | |||||||
| Bсред= k = | 0,00917 |
|
|
|
|
|
| ||||||||
Среднее значение константы скорости по методу наименьших квадратов равно k=0,00917 [л/(моль•ч)]. Причем при умножении на Ск∑ значение константы, рассчитанное по методу наименьших квадратов, примерно совпадает со значением Кнабл, рассчитанным интегральным методом.
Дата: 2019-07-30, просмотров: 301.