Экспериментальные данные по текущим концентрациям приведены для продукта реакции – хлорбензола (С3), поэтому поиск модели будем проводить на их основе.
Рассмотрим первые три опыта, т. к. они отвечают требованию воспроизводимости.
Опишем зависимость концентрации хлорбензола (С3) от времени полиномом 1 степени:
Y=B0+B1t
Матрица Х:
| 1 | 12 |
| 1 | 24 |
| 1 | 36 |
| 1 | 48 |
| 1 | 60 |
| 1 | 72 |
| 1 | 96 |
| 1 | 120 |
Матрица Хт:
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||||
| 12 | 24 | 36 | 48 | 60 | 72 | 96 | 120 | ||||||||||
|
Ковариационная матрица | |||||||||||||||||
| 0,491329 | -0,00626 |
| |||||||||||||||
| -0,00626 | 0,000107 |
|
|
|
|
| |||||||||||
| Матрица(ХтХ) - 1Хт |
|
|
|
|
|
|
| ||||||||||
| 0,416185 | 0,34104 | 0,265896 | 0, 190751 | 0,1156069 | 0,0404624 | -0,10982659 | -0,2601156 |
| |||||||||
| -0,00498 | -0,00369 | -0,00241 | -0,00112 | 0,0001606 | 0,0014451 | 0,00401413 | 0,0065832 |
| |||||||||
Перемножив матрицы (ХтХ) - 1Хт и матрицу средних значений концентраций С3 по повторяющимся опытам, получим значения коэффициентов уравнения полинома.
Матрица В:
| 0,012624 |
| 0,005562 |
| Т, мин | С3(1) | С3(2) | С3(3) | С3средн | C3 расч | ||||||
| 12 | 0,075 | 0,073 | 0,072 | 0,073 | 0,079368 | ||||||
| 24 | 0,14 | 0,147 | 0,141 | 0,143 | 0,146112 | ||||||
| 36 | 0,21 | 0,222 | 0,216 | 0,216 | 0,212856 | ||||||
| 48 | 0,269 | 0,289 | 0,274 | 0,277 | 0,2796 | ||||||
| 60 | 0,357 | 0,333 | 0,362 | 0,351 | 0,346344 | ||||||
| 72 | 0,43 | 0,434 | 0,426 | 0,43 | 0,413088 | ||||||
| 96 | 0,531 | 0,545 | 0,54 | 0,539 | 0,546576 | ||||||
| 120 | 0,656 | 0,692 | 0,676 | 0,675 | 0,680064 | ||||||
| Дисперсия воспроизводимости: Sy=0.00009925 Дисперсия неадекватности: Sнеад=0,000229 Критерий Фишера: F=2.305 Табличное значение Fт(6, 16) =3,2 F<Fт; модель адекватна. Ошибка определения коэффициентов: | |||||||||||
| 70,35924 | 1,03852 | ||||||||||
|
Коэффициент Стьюдента | |||||||||||
| 5573,328 | 186,7177 |
| Т>Tкр | ||||||||
| Коэффициент Стьюдента табличный: | Ткр=2.31 | ||||||||||
Все коэффициенты уравнения значимы, модель адекватна.
Y=0.012624+0.005562
Проверим графически соответствие модели экспериментальным данным.
Для этого построим кривые зависимости текущих концентраций от времени и с помощью линии тренда найдем вид уравнения.
Данные для построения графиков.
| № опыта | 1 | 2 | 3 | 5 |
| Т, мин | С3, моль/л | С3, моль/л | С3, моль/л | С3, моль/л |
| 12 | 0,075 | 0,073 | 0,072 | 0,069 |
| 24 | 0,14 | 0,147 | 0,141 | 0,146 |
| 36 | 0,21 | 0,222 | 0,216 | 0, 202 |
| 48 | 0,269 | 0,289 | 0,274 | 0,282 |
| 60 | 0,357 | 0,333 | 0,362 | 0,338 |
| 72 | 0,43 | 0,434 | 0,426 | 0,402 |
| 96 | 0,531 | 0,545 | 0,54 | 0,575 |
| 120 | 0,656 | 0,692 | 0,676 | 0,69 |
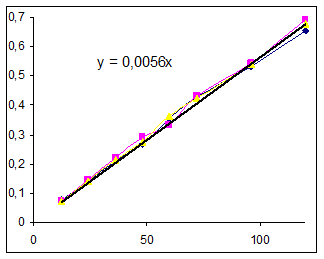
Константы в выражении, полученном графически, сравнимы с расчетными в уравнении полинома. Значения начальных скоростей примерно одинаковы. За истинные будем принимать расчетные значения.
Значение начальной скорости в рассматриваемом опыте: R0=0,0056 (моль/(л ч)).
Определим выражения для скоростей реакций по остальным опытам.
Опыт 4:
Рассчитанное выражение для зависимости концентрации хлорбензола от времени разобранным выше матричным методом:
Y=0.012624+0.005134t
| МатрицаХ: |
|
|
| |||||
| 1 | 13 |
|
|
| ||||
| 1 | 26 |
|
|
| ||||
| 1 | 39 |
|
|
| ||||
| 1 | 52 |
|
|
| ||||
| 1 | 65 |
|
|
| ||||
| 1 | 78 |
|
|
| ||||
| 1 | 104 |
|
|
| ||||
| 1 | 130 |
|
|
| ||||
| Матрица Хт: |
|
|
|
|
|
| ||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 13 | 26 | 39 | 52 | 65 | 78 | 104 | 130 | |
| Матрица Xт·X: |
|
|
|
|
|
| ||
| 8 | 507 |
|
|
| ||||
| 507 | 43095 |
|
|
| ||||
| Ковариационная матрица |
|
|
|
|
| |||
| 0,491329 | -0,00578 |
|
|
| ||||
| -0,00578 | 9,12E-05 |
|
|
| ||||
| Матрица (Xт·X) - 1·Xт: |
|
|
|
|
|
| ||
| 0,416185 | 0,34104 | 0,265896 | 0, 190751 | 0,1156069 | 0,0404624 | -0,10982659 | -0,2601156 | |
| -0,00459 | -0,00341 | -0,00222 | -0,00104 | 0,0001482 | 0,0013339 | 0,003705351 | 0,0060768 | |
| Матрица коэффициентов полинома В: |
|
|
|
| ||||
| 0,012624 |
|
|
|
|
|
|
| |
| 0,005134 |
|
|
|
|
|
|
| |
| Т, мин | С3, моль/л |
| 13 | 0,079 |
| 26 | 0,156 |
| 39 | 0,237 |
| 52 | 0,301 |
| 65 | 0,39 |
| 78 | 0,428 |
| 104 | 0,575 |
| 130 | 0,713 |
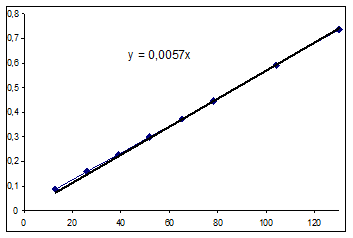
По уравнению кривой, построенной по экспериментальным данным, и расчетному выражению значения начальной скорости близки. Примем как более точное расчетное значение: R0=0,0051 (моль/(л ч)).
Опыт 6.
Определение выражения для скорости матричным методом. Для этого получим выражение для зависимости концентрации от времени и продифференцируем его по времени.
| МатрицаХ: |
|
|
| |||||
| 1 | 20 |
|
| |||||
| 1 | 40 |
|
| |||||
| 1 | 60 |
|
| |||||
| 1 | 80 |
|
| |||||
| 1 | 100 |
|
| |||||
| 1 | 120 |
|
| |||||
| 1 | 160 |
|
| |||||
| 1 | 200 |
|
| |||||
| Матрица Хт: |
|
|
|
|
|
| ||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 20 | 40 | 60 | 80 | 65 | 120 | 160 | 200 | |
| Матрица Xт·X: |
|
|
|
|
|
| ||
| 8 | 780 |
|
|
| ||||
| 745 | 98500 |
|
|
| ||||
| Ковариационная матрица |
|
| ||||||
| 0,491329 | -0,00376 |
|
|
| ||||
| -0,00376 | 3,85E-05 |
|
|
| ||||
| Матрица (Xт·X) - 1·Xт: |
|
|
|
|
|
| ||
| 0,416185 | 0,34104 | 0,265896 | 0, 190751 | 0,1156069 | 0,0404624 | -0,10982659 | -0,2601156 | |
| -0,00299 | -0,00222 | -0,00145 | -0,00067 | 9,634E-05 | 0,0008671 | 0,002408478 | 0,0039499 | |
| МатрицаВ:
|
|
|
|
|
|
|
| |
| 0,013948 | ||||||||
| 0,003627 | ||||||||
Рассчитанное выражение для зависимости концентрации от времени:
Y=0.013948+0.003627t
Найдем графическое выражение.
Экспериментальные данные:
| Т, мин | С3 эксп. |
| 20 | 0,08 |
| 40 | 0,163 |
| 60 | 0,24 |
| 80 | 0,315 |
| 100 | 0,374 |
| 120 | 0,435 |
| 160 | 0,581 |
| 200 | 0,753 |
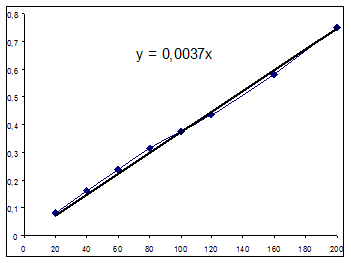
Значения начальных скоростей по графику и расчетное одного порядка, примем расчетное значение за истинное: R=0,0036 (моль/(л ч)).
Опыт 7.
Определение выражения для зависимости текущей концентрации от времени матричным методом.
Матрица Х:
| 1 | 43 |
|
|
|
| 1 | 86 |
|
|
|
| 1 | 129 |
|
|
|
| 1 | 172 |
|
|
|
| 1 | 215 |
|
|
|
| 1 | 258 |
|
|
|
Продолжение.
| 1 | 344 |
|
|
| ||||||
| 1 | 430 |
|
|
| ||||||
| Матрица Хт: |
|
|
|
|
|
| ||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |||
| 43 | 86 | 129 | 172 | 65 | 258 | 344 | 430 | |||
| Матрица Xт·X: |
|
|
|
|
|
| ||||
| 8 | 1677 |
|
|
| ||||||
| 1527 | 439245 |
|
|
| ||||||
| Ковариационная матрица |
|
|
|
|
| |||||
| 0,491329 | -0,00175 |
|
|
| ||||||
| -0,00175 | 8,34E-06 |
|
|
| ||||||
| Матрица(Xт·X) 1·Xт: |
|
|
|
|
|
| ||||
| 0,416185 | 0,34104 | 0,265896 | 0, 190751 | 0,1156069 | 0,0404624 | -0,10982659 | -0,260115 | |||
| -0,00139 | -0,00103 | -0,00067 | -0,00031 | 4,481E-05 | 0,0004033 | 0,001120222 | 0,0018372 | |||
| Матрица коэффициентов полинома В: |
|
|
|
| ||||||
| 0,037746 | ||||||||||
| 0,00153 | ||||||||||
Уравнение зависимости выглядит следующим образом:
Y=0.037746+0.00153t
Определение графическим способом.
Экспериментальные данные:
| Т, мин | С3 эксп. |
| 43 | 0,08 |
| 86 | 0,173 |
| 129 | 0,234 |
| 172 | 0,308 |
| 215 | 0,384 |
| 258 | 0,443 |
| 344 | 0,574 |
| 430 | 0,672 |
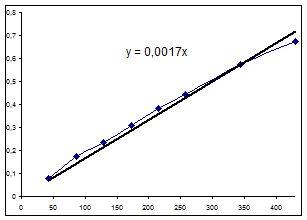
Значение начальной скорости: R=0,0015 (моль/(л ч)).
Опыт 8.
Нахождение вида зависимости концентрации от времени матричным способом.
Матрица Х:
| 1 | 6 |
|
| |||||||
| 1 | 12 |
|
| |||||||
| 1 | 18 |
|
| |||||||
| 1 | 24 |
|
| |||||||
| 1 | 30 |
|
| |||||||
| 1 | 36 |
|
| |||||||
| 1 | 48 |
|
| |||||||
| 1 | 60 |
|
| |||||||
| Матрица Хт: |
|
|
|
|
|
| ||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |||
| 6 | 12 | 18 | 24 | 65 | 36 | 48 | 60 | |||
| Матрица Xт·X: |
|
|
|
|
|
| ||||
| 8 | 234 |
|
|
| ||||||
| 269 | 10230 |
|
|
| ||||||
| Ковариационная матрица |
|
|
|
|
| |||||
| 0,491329 | -0,01252 |
|
|
| ||||||
| -0,01252 | 0,000428 |
|
|
| ||||||
| Матрица(XтX) 1Xт: |
|
|
|
|
|
| ||||
| 0,416185 | 0,34104 | 0,265896 | 0, 190751 | 0,1156069 | 0,0404624 | -0,10982659 | -0,260115 | |||
| -0,00996 | -0,00739 | -0,00482 | -0,00225 | 0,0003211 | 0,0028902 | 0,008028259 | 0,0131663 | |||
| Матрица коэффициентов полинома В: |
|
|
|
| ||||||
| 0,008006 | ||||||||||
| 0,011508 | ||||||||||
Графический метод.
Экспериментальные данные:
| Т, мин | С3 эксп. |
| 6 | 0,073 |
| 12 | 0,14 |
| 18 | 0,22 |
| 24 | 0,285 |
| 30 | 0,353 |
| 36 | 0,427 |
| 48 | 0,575 |
| 60 | 0,684 |
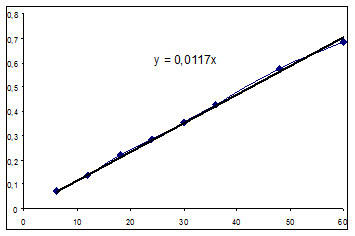
Выражение, полученное матричным методом:
Y=0.008006+0.011508t
Значение начальной скорости: R=0,0115 (моль/(л ч)).
Опыт 9.
Расчет матричным методом.
Матрица Х:
| 1 | 4 |
|
|
| ||||||
| 1 | 8 |
|
|
| ||||||
| 1 | 12 |
|
|
| ||||||
| 1 | 16 |
|
|
| ||||||
| 1 | 20 |
|
|
| ||||||
| 1 | 24 |
|
|
| ||||||
| 1 | 32 |
|
|
| ||||||
| 1 | 40 |
|
|
| ||||||
| Матрица Хт: |
|
|
|
|
|
| ||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |||
| 4 | 8 | 12 | 16 | 65 | 24 | 32 | 40 | |||
| Матрица Xт·X: |
|
|
|
|
|
| ||||
| 8 | 156 |
|
|
| ||||||
| 201 | 4980 |
|
|
| ||||||
| Ковариационная матрица: |
|
|
|
|
| |||||
| 0,491329 | -0,01879 |
|
|
| ||||||
| -0,01879 | 0,000963 |
|
|
| ||||||
| Матрица(Xт·X) 1·Xт: |
|
|
|
|
|
| ||||
| 0,416185 | 0,34104 | 0,265896 | 0, 190751 | 0,1156069 | 0,0404624 | -0,10982659 | -0,260115 | |||
| -0,01493 | -0,01108 | -0,00723 | -0,00337 | 0,0004817 | 0,0043353 | 0,012042389 | 0,0197495 | |||
| Матрица коэффициентов полинома В: |
|
|
|
| ||||||
| 0,011139 | ||||||||||
| 0,016717 | ||||||||||
Уравнение будет выглядеть:
Y=0.011139+0.016717t
Графический метод.
Экспериментальные данные:
| Т, мин | С3 эксп. |
| 4 | 0,073 |
| 8 | 0,142 |
| 12 | 0, 204 |
| 16 | 0,283 |
| 20 | 0,359 |
| 24 | 0,419 |
| 32 | 0,547 |
| 40 | 0,67 |
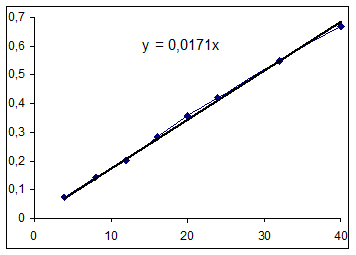
Значение начальной скорости: R=0,0167 (моль/(л ч)).
Дата: 2019-07-30, просмотров: 301.