Следует помнить, что генерация произвольного случайного числа состоит из двух этапов:
· генерация нормализованного случайного числа (то есть равномерно распределенного от 0 до 1);
· преобразование нормализованных случайных чисел ri в случайные числа xi, которые распределены по необходимому пользователю (произвольному) закону распределения или в необходимом интервале.
Генераторы случайных чисел (ГСЧ) по способу получения чисел делятся на:
µ физические;
µ табличные;
µ алгоритмические.
Физические ГСЧ
Примером физических ГСЧ могут служить: монета («орел» — 1, «решка» — 0); игральные кости; поделенный на секторы с цифрами барабан со стрелкой; аппаратурный генератор шума (ГШ), в качестве которого используют шумящее тепловое устройство, например, транзистор (рис.1).
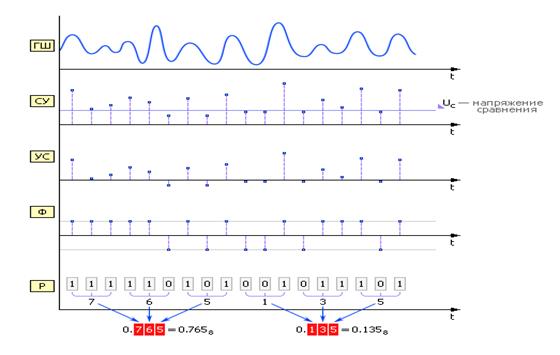
Рис.5 Диаграмма получения случайных чисел аппаратным методом
Табличные ГСЧ
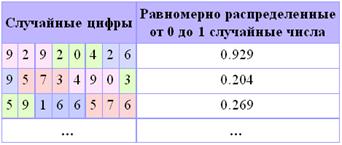
Табличные ГСЧ в качестве источника случайных чисел используют специальным образом составленные таблицы, содержащие проверенные некоррелированные, то есть никак не зависящие друг от друга, цифры. В таблице 1 приведен небольшой фрагмент такой таблицы. Обходя таблицу слева направо сверху вниз, можно получать равномерно распределенные от 0 до 1 случайные числа с нужным числом знаков после запятой (в нашем примере мы используем для каждого числа по три знака). Так как цифры в таблице не зависят друг от друга, то таблицу можно обходить разными способами, например, сверху вниз, или справа налево, или, скажем, можно выбирать цифры, находящиеся на четных позициях.
Таблица 1. Случайные цифры.
Алгоритмические ГСЧ
Числа, генерируемые с помощью этих ГСЧ, всегда являются псевдослучайными (или квазислучайными), то есть каждое последующее сгенерированное число зависит от предыдущего: 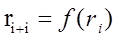
Различают следующие алгоритмические методы получения ГСЧ:
Ø метод серединных квадратов;
Ø метод серединных произведений;
Ø метод перемешивания;
Ø линейный конгруэнтный метод.
Метод серединных квадратов. Имеется некоторое четырехзначное число R0. Это число возводится в квадрат и заносится в R1. Далее из R1 берется середина (четыре средних цифры) — новое случайное число — и записывается в R0. Затем процедура повторяется (см. рис. 2). Отметим, что на самом деле в качестве случайного числа берется число с приписанным слева нулём и десятичной точкой.
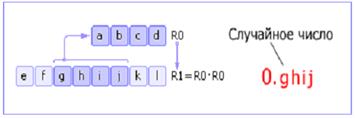
Рис.6 Схема метода средних квадратов
Этот способ был предложен Джоном фон Нейманом и относится к 1946 году.
Метод серединных произведений. Число R0 умножается на R1, из полученного результата R2 извлекается середина R2* (это очередное случайное число) и умножается на R1. По этой схеме вычисляются все последующие случайные числа (см. рис. 3).
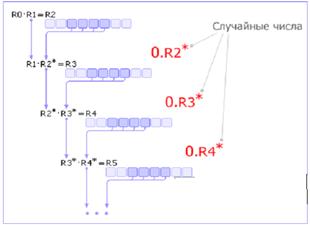
Рис.7 Схема метода серединных произведений
Линейный конгруэнтный метод. Линейный конгруэнтный метод является одной из простейших и наиболее употребительных в настоящее время процедур, имитирующих случайные числа. В этом методе используется операция mod(x, y), возвращающая остаток от деления первого аргумента на второй. Каждое последующее случайное число рассчитывается на основе предыдущего случайного числа по следующей формуле:
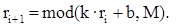
M — модуль (0 < M);
k — множитель (0 ≤ k < M);
b — приращение (0 ≤ b < M);
r0 — начальное значение (0 ≤ r0 < M).
Последовательность случайных чисел, полученных с помощью данной формулы, называется линейной конгруэнтной последовательностью. Многие авторы называют линейную конгруэнтную последовательность при b = 0 мультипликативным конгруэнтным методом, а при b ≠ 0 — смешанным конгруэнтным методом.
Глава 3. Практическая часть
Постановка задачи
На станцию технического обслуживания (СТО) согласно закону Эрланга второго порядка со средним временем прибытия 14 мин прибывают автомобили для технического обслуживания (36% автомобили) и ремонта (64% автомобилей).
На СТО есть два бокса для технического обслуживания и три бокса для ремонта. Выполнение простого, средней сложности и сложного ремонтов - равновероятно.
Время и стоимость выполнения работ по техническому обслуживанию и ремонту зависит от категории выполняемых работ (табл. 2).
После технического обслуживания 12% автомобилей поступают для выполнения ремонта средней сложности.
Построить гистограмму времени обслуживания автомобилей.
Оценить выручку СТО за пять дней работы.
Таблица 2.
| Категория работ | Время ремонта, мин | Стоимость ремонта, руб |
| Техническое обслуживание | Равномерно распределено в интервале 10-55 | Равномерно распределено в интервале 100-400 |
| Простой ремонт | Равномерно распределено в интервале 12-45 | Равномерно распределено в интервале 50-450 |
| Ремонт средней сложности | Нормально распределено со средним 45 и среднеквадр-ым отклонением 5 | Равномерно распределено в интервале 100-1400 |
| Сложный ремонт | Равномерно распределено в интервале 80-150 | Равномерно распределено в интервале 350-2550 |
Упрощенная схема объекта моделирования:
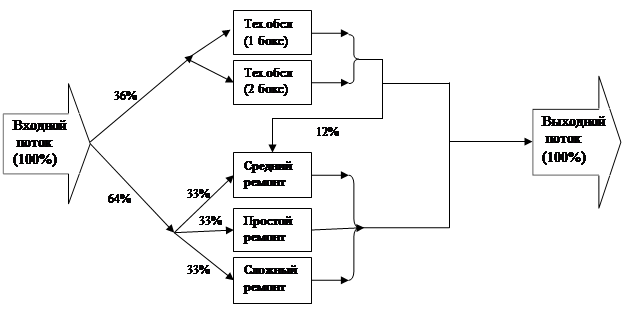
Рис.8 Схема моделирования работы станции технического обслуживания
Описание метода решения
Дата: 2019-07-30, просмотров: 326.