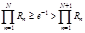Содержание
Введение
Глава1. Моделирование систем массового обслуживания
1.1. Структура и параметры эффективности и качества функционирования СМО
1.2 Классификация СМО и их основные элементы
1.3 Процесс имитационного моделирования
Глава 2. Распределения и генераторы псевдослучайных чисел
2.1 Виды распределений
2.2 Виды генераторов случайных чисел
Глава 3. Практическая часть
3.1 Постановка задачи
3.2 Описание метода решения задачи вручную
3.3 Блок-схема
3.4 Перевод модели на язык программирования
Заключение
Список использованной литературы
ВВЕДЕНИЕ
Во многих областях практической деятельности человека мы сталкиваемся с необходимостью пребывания в состоянии ожидания. Подобные ситуации возникают в очередях в билетных кассах, в крупных аэропортах, при ожидании обслуживающим персоналом самолетов разрешения на взлет или посадку, на телефонных станциях в ожидании освобождения линии абонента, в ремонтных цехах в ожидании ремонта станков и оборудования, на складах снабженческо-сбытовых организаций в ожидании разгрузки или погрузки транспортных средств. Во всех перечисленных случаях имеем дело с массовостью и обслуживанием. Изучением таких ситуаций занимается теория массового обслуживания.
В теории систем массового обслуживания (в дальнейшем просто – CMО) обслуживаемый объект называют требованием. В общем случае под требованием обычно понимают запрос на удовлетворение некоторой потребности, например, обслуживание автомобиля на заправочной станции, разговор с абонентом, посадка самолета, покупка билета, получение материалов на складе и т.д
На первичное развитие теории массового обслуживания оказали особое влияние работы датского ученого А.К. Эрланга (1878-1929).
Теория массового обслуживания – область прикладной математики, занимающаяся анализом процессов в системах производства, обслуживания, управления, в которых однородные события повторяются многократно, например, на предприятиях бытового обслуживания; в системах приема, переработки и передачи информации; автоматических линиях производства и др.
Задача теории массового обслуживания – установить зависимость результирующих показателей работы системы массового обслуживания (вероятности того, что заявка будет обслужена; математического ожидания числа обслуженных заявок и т.д.) от входных показателей (количества каналов в системе, параметров входящего потока заявок и т.д.). Результирующими показателями или интересующими нас характеристиками СМО являются – показатели эффективности СМО, которые описывают способна ли данная система справляться с потоком заявок.
В теории СМО рассматриваются такие случаи, когда поступление требований происходит через случайные промежутки времени, а продолжительность обслуживания требований не является постоянной, т.е. носит случайный характер. В силу этих причин одним из основных методов математического описания СМО является аппарат теории случайных процессов .
Основной задачей теории СМО является изучение режима функционирования обслуживающей системы и исследование явлений, возникающих в процессе обслуживания. Так, одной из характеристик обслуживающей системы является время пребывания требования в очереди. Очевидно, что это время можно сократить за счет увеличения количества обслуживающих устройств. Однако каждое дополнительное устройство требует определенных материальных затрат, при этом увеличивается время бездействия обслуживающего устройства из-за отсутствия требований на обслуживание, что также является негативным явлением. Следовательно, в теории СМО возникают задачи оптимизации: каким образом достичь определенного уровня обслуживания (максимального сокращения очереди или потерь требований) при минимальных затратах, связанных с простоем обслуживающих устройств.
Имитационное моделирование реализуются программно с использованием различных языков, как универсальных - БЕЙСИК, РАСКАЛЬ, СИ и т.д., так и специализированных, предназначенных для построения имитационных моделей - СИМСКРИПТ, СТАМ/КЛАСС, GPSS, SLAM, Pilgrim и др.
Цель курсовой работы по дисциплине «Имитационное моделирование экономических процессов» - ознакомление с современными концепциями построения моделирующих систем, с основными приемами имитационного моделирования, встраиваемыми в общую процедуру преобразования информации от структурирования и формализации составляющих предметных областей до интерпретации обработанных данных и приобретенных знаний, связанных с описанием экономических процессов.
Данная работа представляет собой работу по созданию и реализации математической модели системы массового обслуживания для получения необходимых нам результатов на основании исходных данных и известных математических зависимостей. Целью данной курсовой работы является анализ и моделирование работы станции технического обслуживания, создав программу на языке С++, имитирующую ее работу; сравнение полученных результатов моделирующей программы с результатами работы реального объекта.
Виды распределений
Равномерное распределение
Функция плотности вероятности равномерного распределения задает одинаковую вероятность для всех значений, лежащих между минимальным и максимальным значениями переменной. Другими словами, вероятность того, что значение попадает в указанный интервал. пропорциональна длине этого интервала. Применение равномерного распределения часто вызвано полным отсутствием информации о случайной величине, кроме ее предельных значений. Равномерное распределение называют также прямоугольным.
f (t) =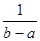 
при а ≤ t ≤ Ь.
Среднее значение распределения равно μ =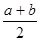 
, дисперсия равна σ2= 
.
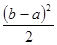Равномерно распределенная случайная величина X на отрезке [а, b] выражается через равномерно распределенную на отрезке [0, 1] случайную величину R формулой
X = а + (b - а) *R
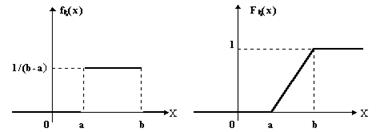
Рис.1 Графики функции распределения и плотности распределения:
Треугольное распределение
Треугольное распределение является более информативным, чем равномерное. Для этого распределения определяются три величины - минимум, максимум и мода. График функции плотности состоит из двух отрезков прямых, одна из которых возрастает при изменении X от минимального значения до моды, а другая убывает при изменении X от значения моды до максимума. Значение математического ожидания треугольного распределения равно одной трети суммы минимума, моды и максимума. Треугольное распределение используется тогда, когда известно наиболее вероятное значение на некотором интервале и предполагается кусочно-линейный характер функции плотности. Функция плотности вероятности треугольного распределения имеет вид:
|
|
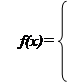
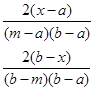
μ=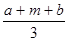 
, σ2= 
.
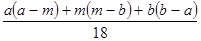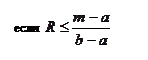
Треугольно распределенная случайная X связана со случайной величиной R, распределенной равномерно на [0,1], соотношением:
|
.
|
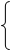
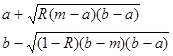
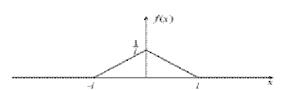
Рис.2 График плотности треугольного распределения
Распределение Пуассона
Распределение Пуассона является дискретным и обычно связано с числом результатов за определенный период времени. Если продолжительность интервалов между результатами распределена экспоненциально, и в каждый момент времени может произойти только один результат, то можно доказать, что число результатов на фиксированном интервале времени распределено по закону Пуассона. Другими словами, если интервалы между прибытиями распределены экспоненциально, распределение числа прибытий будет пуассоновским.
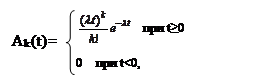
где λ>0, k≥0 - параметры закона. Пуассоновское распределение используется часто как аппроксимация биномиального распределения в том случае, когда оно моделирует последовательности независимых испытаний Бернулли (результаты таких испытаний могут быть типа «да-нет», «стоять-идти», «успех-неудача» и т.п.). При больших значениях математического ожидания пуассоновское распределение аппроксимируется нормальным.
Для получения пуассоновски распределенной случайной величины Y можно воспользоваться следующим методом: установить значение величины Y равным первому значению N, такому, что
|
где Rn – п-е псевдослучайное число.
Нормальное распределение
Нормальное, или Гауссово, распределение является наиболее важным в теории вероятностей и математической статистике. Эту роль нормальное распределение приобрело в связи с центральной предельной теоремой, которая утверждает, что при весьма нестрогих условиях распределение средней величины или суммы N независимых наблюдений из любого распределения стремиться к нормальному по мере увеличения N. Таким образом, сумму случайных величин часто можно считать нормально распределенной.
Именно благодаря центральной предельной теореме нормальное распределение так часто применяется в исследованиях по теории вероятностей и математической статистике. Существует и другая причина частого применения нормального распределения. Его преимуществом является легкость математического трактования, в связи с чем многие методы доказательств в таких областях, как, например, регрессионный или вариационный анализ, основаны на предположении о нормальном характере функции плотности.
При больших значениях среднего нормальное распределение является хорошей аппроксимацией биноминального распределения.
Функция плотности вероятности нормального закона имеет вид:
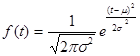
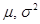- параметры нормального закона, ( 
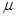- среднее значение, 
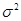- дисперсия нормального распределения).
Генератор нормально распределенной случайной величины X можно получить по формулам:
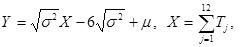
где Tj (j=1,…,12) – значения независимых случайных величин, равномерно распределенных на интервале (0,1).
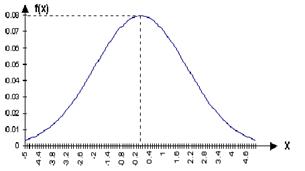
Рис. 4 График плотности вероятности имеет вид нормальной кривой (Гаусса)
Физические ГСЧ
Примером физических ГСЧ могут служить: монета («орел» — 1, «решка» — 0); игральные кости; поделенный на секторы с цифрами барабан со стрелкой; аппаратурный генератор шума (ГШ), в качестве которого используют шумящее тепловое устройство, например, транзистор (рис.1).
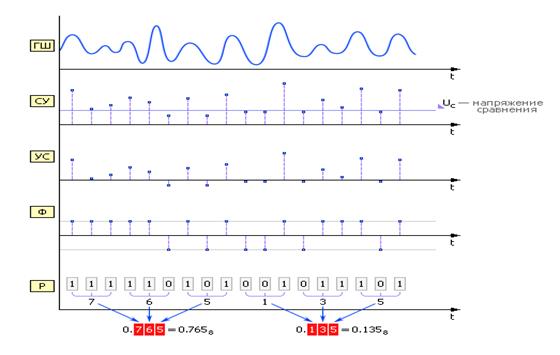
Рис.5 Диаграмма получения случайных чисел аппаратным методом
Табличные ГСЧ
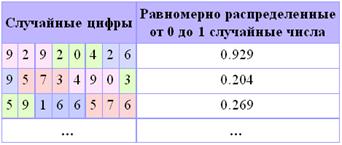
Табличные ГСЧ в качестве источника случайных чисел используют специальным образом составленные таблицы, содержащие проверенные некоррелированные, то есть никак не зависящие друг от друга, цифры. В таблице 1 приведен небольшой фрагмент такой таблицы. Обходя таблицу слева направо сверху вниз, можно получать равномерно распределенные от 0 до 1 случайные числа с нужным числом знаков после запятой (в нашем примере мы используем для каждого числа по три знака). Так как цифры в таблице не зависят друг от друга, то таблицу можно обходить разными способами, например, сверху вниз, или справа налево, или, скажем, можно выбирать цифры, находящиеся на четных позициях.
Таблица 1. Случайные цифры.
Алгоритмические ГСЧ
Числа, генерируемые с помощью этих ГСЧ, всегда являются псевдослучайными (или квазислучайными), то есть каждое последующее сгенерированное число зависит от предыдущего: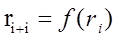 
Различают следующие алгоритмические методы получения ГСЧ:
Ø метод серединных квадратов;
Ø метод серединных произведений;
Ø метод перемешивания;
Ø линейный конгруэнтный метод.
Метод серединных квадратов. Имеется некоторое четырехзначное число R0. Это число возводится в квадрат и заносится в R1. Далее из R1 берется середина (четыре средних цифры) — новое случайное число — и записывается в R0. Затем процедура повторяется (см. рис. 2). Отметим, что на самом деле в качестве случайного числа берется число с приписанным слева нулём и десятичной точкой.
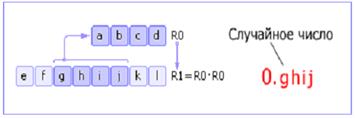
Рис.6 Схема метода средних квадратов
Этот способ был предложен Джоном фон Нейманом и относится к 1946 году.
Метод серединных произведений. Число R0 умножается на R1, из полученного результата R2 извлекается середина R2* (это очередное случайное число) и умножается на R1. По этой схеме вычисляются все последующие случайные числа (см. рис. 3).
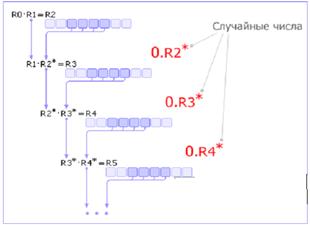
Рис.7 Схема метода серединных произведений
Линейный конгруэнтный метод. Линейный конгруэнтный метод является одной из простейших и наиболее употребительных в настоящее время процедур, имитирующих случайные числа. В этом методе используется операция mod(x, y), возвращающая остаток от деления первого аргумента на второй. Каждое последующее случайное число рассчитывается на основе предыдущего случайного числа по следующей формуле:
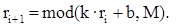
M — модуль (0 < M);
k — множитель (0 ≤ k < M);
b — приращение (0 ≤ b < M);
r0 — начальное значение (0 ≤ r0 < M).
Последовательность случайных чисел, полученных с помощью данной формулы, называется линейной конгруэнтной последовательностью. Многие авторы называют линейную конгруэнтную последовательность при b = 0 мультипликативным конгруэнтным методом, а при b ≠ 0 — смешанным конгруэнтным методом.
Глава 3. Практическая часть
Постановка задачи
На станцию технического обслуживания (СТО) согласно закону Эрланга второго порядка со средним временем прибытия 14 мин прибывают автомобили для технического обслуживания (36% автомобили) и ремонта (64% автомобилей).
На СТО есть два бокса для технического обслуживания и три бокса для ремонта. Выполнение простого, средней сложности и сложного ремонтов - равновероятно.
Время и стоимость выполнения работ по техническому обслуживанию и ремонту зависит от категории выполняемых работ (табл. 2).
После технического обслуживания 12% автомобилей поступают для выполнения ремонта средней сложности.
Построить гистограмму времени обслуживания автомобилей.
Оценить выручку СТО за пять дней работы.
Таблица 2.
| Категория работ | Время ремонта, мин | Стоимость ремонта, руб |
| Техническое обслуживание | Равномерно распределено в интервале 10-55 | Равномерно распределено в интервале 100-400 |
| Простой ремонт | Равномерно распределено в интервале 12-45 | Равномерно распределено в интервале 50-450 |
| Ремонт средней сложности | Нормально распределено со средним 45 и среднеквадр-ым отклонением 5 | Равномерно распределено в интервале 100-1400 |
| Сложный ремонт | Равномерно распределено в интервале 80-150 | Равномерно распределено в интервале 350-2550 |
Упрощенная схема объекта моделирования:
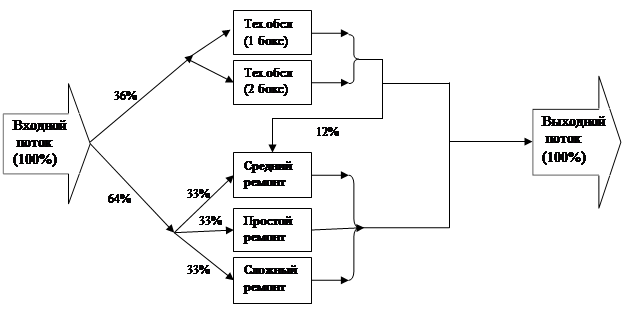
Рис.8 Схема моделирования работы станции технического обслуживания
Описание метода решения
Таблица 3.
| № | Случайные числа, g i | Время поступления требований, | Блоки, на которые поступают машины |
| 1 | 0,0850 | 34,51 | Тех.обслуживание |
| 2 | 0,2369 | 20,16 | Тех.обслуживание |
| 3 | 0,3412 | 15,05 | Тех.обслуживание |
| 4 | 0,9304 | 1,01 | Слож. ремонт |
| 5 | 0,9716 | 0,40 | Слож. ремонт |
| 6 | 0,1184 | 29,87 | Тех.обслуживание |
| 7 | 0,2838 | 17,63 | Тех.обслуживание |
| 8 | 0,2065 | 22,08 | Тех.обслуживание |
| 9 | 0,0139 | 59,86 | Тех.обслуживание + сред. ремонт |
| 10 | 0,6523 | 5,98 | Средний ремонт |
| 11 | 0,4056 | 12,63 | Простой ремонт |
| 12 | 0,6892 | 5,21 | Средний ремонт |
| 13 | 0,8028 | 3,08 | Слож. ремонт |
| 14 | 0,1368 | 27,85 | Тех.обслуживание |
| 15 | 0,3270 | 15,65 | Тех.обслуживание |
| 16 | 0,6431 | 6,18 | Средний ремонт |
| 17 | 0,6446 | 6,15 | Средний ремонт |
| 18 | 0,8252 | 2,69 | Слож. ремонт |
| 19 | 0,2025 | 22,36 | Тех.обслуживание |
| 20 | 0,6429 | 6,18 | Средний ремонт |
| 21 | 0,9519 | 0,69 | Слож. ремонт |
| 22 | 0,1202 | 29,66 | Тех.обслуживание |
| 23 | 0,9800 | 0,28 | Слож. ремонт |
| 24 | 0,1061 | 31,41 | Тех.обслуживание |
| 25 | 0,1841 | 23,69 | Тех.обслуживание |
| 26 | 0,6490 | 6,05 | Средний ремонт |
| 27 | 0,0809 | 35,20 | Тех.обслуживание |
| 28 | 0,2589 | 18,92 | Тех.обслуживание |
| 29 | 0,9340 | 0,96 | Слож. ремонт |
| 30 | 0,4139 | 12,35 | Простой ремонт |
Согласно условию задачи 36% автомобилей поступают на техническое обслуживание, а остальные 64% - на ремонт. Сравниваем доли процентов со случайными числами и, таким образом, определяем, какой именно автомобиль куда поступает:
· если g < 0.36, то на тех. обслуживание;
· если g > 0.36, то на ремонт.
Итого, из потока, поступающих на заправочную станцию 30 автомобилей, 15 автомобилей поступают на тех. обслуживание и 15 - на ремонт.
Далее, умножаем случайные числа, которые меньше 0,36 на 2,78. Это мы делаем для того, чтобы получить 100% из тех 36% машин, которые приехали на тех. обслуживание. Это поможет найти те самые 12% машин, которые после тех. обслуживания поступают на выполнение ремонта средней сложности. Полученные числа сравниваем – если число меньше или равно 0,12, то она после тех.обслуживания поступает и на средний ремонт. После произведенных вычислений мы определили, что 7ая машина, поступившая на тех. обслуживание, поступила также и на ремонт средней сложности.
Далее используем тот же метод для определения того, какие машины, поступившие на ремонт, поступили на простой, средний и сложный ремонты. Умножаем случайные числа, которые больше 0,36 на 1,56. Получившиеся числа сравниваем:
· если число < 0,33 – простой ремонт;
· если число находится в промежутке от 0,33 до 0,66 – средний ремонт;
· если число > 0,66 – сложный ремонт.
Далее определяем время на обслуживание автомобилей.
Ë Время на тех. обслуживание равномерно распределено в интервале 10-55:
Xтоi = gi (55 - 10) + 10
Стоимость тех.обслуживания также равномерно распределена в интервале 100-400:
Xтоi = gi (400 - 100) + 100
Таблица 4.
| № | Случайные числа, g i | Время обслуживания, мин | Случайные числа, g i | Стоимость обслуживания, руб |
| 1 | 0,3051 | 23,7295 | 0,663788 | 299,1364 |
| 2 | 0,4534 | 30,403 | 0,131907 | 139,5721 |
| 3 | 0,6705 | 40,1725 | 0,413686 | 224,1058 |
| 4 | 0,8613 | 48,7585 | 0,807198 | 342,1594 |
| 5 | 0,8378 | 47,701 | 0,950983 | 385,2949 |
| 6 | 0,1666 | 17,497 | 0,527365 | 258,2095 |
| 7 | 0,1816 | 18,172 | 0,735827 | 320,7481 |
| 8 | 0,0582 | 12,619 | 0,05409 | 116,227 |
| 9 | 0,0319 | 11,4355 | 0,022308 | 106,6924 |
| 10 | 0,382 | 27,19 | 0,105635 | 131,6905 |
| 11 | 0,5775 | 35,9875 | 0,817392 | 345,2176 |
| 12 | 0,5199 | 33,3955 | 0,599275 | 279,7825 |
| 13 | 0,8518 | 48,331 | 0,281503 | 184,4509 |
| 14 | 0,999 | 54,955 | 0,703246 | 310,9738 |
| 15 | 0,6651 | 39,9295 | 0,158009 | 147,4027 |
Для определения общей стоимости тех. обслуживания сложим все отдельные стоимости:
299,14 + 139,57 + 224,1 + 342,16 + 385,29 + 258,2 + 320,75 + 116,23 + 106,69 + 131,69 + 345,22 + 279,78 + 184,45 + 310,97 + 147,4 = 3591,664
Ë Время на простой ремонт равномерно распределено в интервале 12-45:
Xпрi = gi (45 - 12) + 12
Стоимость простого ремонта также равномерно распределена в интервале 50-450:
Xпрi = gi (450 - 50) + 50
Таблица 5.
| № | Случайные числа, g i | Время ремонта, мин. | Случайные числа, g i | ||
Стоимость ремонта, руб.
280,7096
219,3844
500,094
Ë Время на средний ремонт имеет экспоненциальное распределение со средним 45 и среднеквадратическим отклонением 5:
Xслi =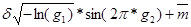 
Стоимость среднего ремонта также равномерно распределена в интервале 100-1400:
Xслi = gi (1400 - 100) + 100
Таблица 6.
| № | Случайные числа, g 1 i | Случайные числа, g 2 i | Время ремонта, мин. | Случайные числа, g i | ||
Стоимость ремонта, руб.
726,3686
145,0411
1080,694
352,2637
1207,727
1112,523
949,7983
5574,416
Ë Время на сложный ремонт равномерно распределено в интервале 80-150:
Xпрi = gi (150 - 80) + 80
Стоимость сложного ремонта также равномерно распределена в интервале 350-2550:
Xпрi = gi (2550 - 350) + 350
Таблица 7.
| № | Случайные числа, g i | Время ремонта, мин. | Случайные числа, g i | ||
Стоимость ремонта, руб.
2179,37
1738,851
2167,288
2353,267
859,8126
1122,224
954,7558
11375,57
Нужно определить среднее время обслуживания автомобилей на СТО. Для этого сначала определяем среднее время обслуживания для ТО, простого, среднего и сложного ремонтов в отдельности.
Ø Среднее время тех. обслуживания = общее время тех. обслуживания / число обслуживающихся машин. = 480 / 15 = 32 мин.
Ø Среднее время простого ремонта = общее время простого ремонта / число обслуживающихся машин. = (50+43) / 2 = 46,5 мин.
Ø Среднее время среднего ремонта = общее время среднего ремонта / число обслуживающихся машин. = 466 / 7 = 66,57 мин.
Ø Среднее время сложного ремонта = общее время сложного ремонта / число обслуживающихся машин. = (64+27+27+66+37) / 7 = 31,57 мин.
Ø Общая стоимость обслуживания на СТО = 3591,664 + 500,094 + 5574,416 + 11375,57 =
21041,74 руб.
Итого среднее время обслуживания автомобилей = (32+46,5+66,57+31,57) / 4 = 44,16 мин.
Для более детального моделирования работы заправочной станции, изобразим нашу СМО в виде графика (график прилагается к работе в виде Приложения).
Интервал времени обслуживания всех машин на графике составляет 546 мин. Имеется 5 обслуживающих блоков: 2 блока для ТО, и по 1 блоку на простой, средний и сложный ремонты.
В каналы поступает один тип заявок – неприоритетные, т.е. поступающие заявки упорядочиваются в очереди и поступают на обслуживание в порядке поступления (первый пришел – первый обслужен).
Канал может обслуживать одновременно только одну заявку. Обслуживание заявок производится в таком порядке: сначала в очереди нет ни одной машины, и колонка свободна. В момент поступления машины начинается его обслуживание. Если следующая машина приезжает в тот момент, когда канал занят, то она становится в очередь. Далее дисциплина обслуживания такова: обслуживается машина, стоящая первая в очереди.
(См. Приложение).
По полученному графику определяем следующие характеристики работы СМО:
« Среднее время задержки (автомобилей):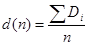 
Тех. обслуживание: (11+38+26) /3 = 25
Простой ремонт: нет задержки
Средний ремонт: 265 / 6 = 44,2
Сложный ремонт: 42 / 2 =21
« Средняя длина очереди (автомобилей):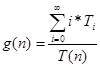 
,
Где: T ( n ) – конечное время работы системы;
T 0 , T 1 , T 2 … - промежуток времени, в течении которого в системе находилось соответственно 0, 1, 2 и более требований.
Тех. обслуживание: T ( n )=546; T 0=471; T 1=75; g ( n ) = 75 / 546 = 0,14
Простой ремонт: нет очереди
Средний ремонт: T ( n )=515; T 0=249; T 1=128, T 2=108, T 3=29; g ( n ) = (128+108*2+29*3) / 515 = 0,84
Сложный ремонт: T ( n )=493; T 0=451; T 1=42; g ( n ) = 42 / 491 = 0,09
« Максимальная длина очереди (автомобилей): L ( max ) = 3 машины
« Коэффициент использования устройства (блоков на СТО):
; 
;
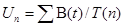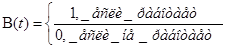Тех. обслуживание: Un = 480 / 546 = 0,88 => 88% - работает, 12% - простой;
Простой ремонт: Un = 92/ 517 = 0,18 => 18% - работает, 72% - простой;
Средний ремонт: Un = 316 / 546 = 0,61 => 61% - работает, 39% - простой;
Сложный ремонт: Un = 221 / 546 = 0,45 => 45% - работает, 55% - простой.
Блок – схема
3.4 Перевод модели на язык программирования
Программа
Принятые сокращения:
tk – количество минут (в нашей программе tk = 7200, т.е. 5 дней);
kol – количество машин, прибывших на СТО за 5 дней;
st – счетчик машин, поступивших на СТО за 5 дней;
i – переменная;
j – кол-во машин, поступивших на тех. обслуживание;
r 1 - кол-во машин, поступивших на простой ремонт;
r 2- кол-во машин, поступивших на средний ремонт;
r 3- кол-во машин, поступивших на сложный ремонт;
k , l , m , n – переменные;
p – случайное число;
s _ to – выручка на блоке тех. обслуживания за 5 дней;
s _ pr – выручка по простому ремонту за 5 дней;
s _ sr – выручка по среднему ремонту за 5 дней;
s _ sl – выручка по сложному ремонту за 5 дней;
SUM – общая выручка на СТО за 5 дней.
Программный код :
#include<iostream.h>
#include<math.h>
#include<stdio.h>
#include<conio.h>
#include<stdlib.h>
void main()
{
int tk,kol,i=0,j=0,r1=0,r2=0,r3=0,k=1,l=1,m=1,n=1;
float p, st=0, s_to=0, s_pr=0, s_sr=0, s_sl=0, SUM;
cin>>tk;
while (st<=tk)
{
p = - log(rand()))/32767*14;
st=st+p;
i++;
}
kol=i;
for (i=1; i<=kol; i++)
{
p=float(rand())/32767;
if (p<=0,12) {j++; r2++;}
else if (p>0,12 && p<=0,36) j++;
else if (p>0,36 && p<=0,57) r1++;
else if (p>0,57 && p<=0,78) r2++;
else r3++;
}
while (k<=j)
{
p= float(rand())/32767*300+100;
s_to=s_to+p;
k++;
}
while (l<=r1)
{
p=float(rand())/32767*400+50;
s_pr=s_pr+p;
l++;
}
while (m<=r2)
{
p=float(rand())/32767*1300+100;
s_to=s_to+p;
k++;
}
while (n<=r3)
{
p=float(rand())/32767*2200+350;
s_sl=s_sl+p;
n++;
}
SUM=s_to+s_pr+s_sr+s_sl;
cout<<"viruchka za 5 dnei ravna"<<SUM<<endl;
}
Рис.9 Результат выполнения программы
Заключение
Широкое внедрение электронно-вычислительной техники во все сферы нашей жизни в последнее время, вызвало бурный рост технологий, связанных с применением в них средств вычислительной техники. Одной из наиболее крупных отраслей развития технологий с применением ЭВМ, является математическое моделирование, которое достаточно просто (в отличие от аналогового моделирования) может быть реализовано на ЭВМ разных модификаций и возможностей. Связано это с тем, что при математическом моделировании модель представляет собой определенную последовательность математических зависимостей и динамика такой модели представляет собой изменение параметров зависимостей в результате выполнения расчетов. Математическое моделирование тесно связано с имитационным моделированием. Одним из разделов математического моделирования, являются модели систем массового обслуживания и их изучение.
В данном курсовом проекте была построена имитационная модель СТО с использованием программы С++, при этом мы использовали программу моделирования процесса с N обрабатывающими устройствами и с очередью. В результате моделирования мы вычислили: выручку на СТО за 5 дней, построили график обслуживания автомобилей, программу и блок-схему.
Список использованной литературы
1. Емельянов А.А. «имитационное моделирование экономических процессов» 2002г
2. Советов В.Я., Яковлев С.А. «Моделирование системы» 2001г.
3. Соболь И.М. «Метод Монте-Карло» 1968г.
4. Шеннон Р. «Имитационное моделирование систем – искусства и науки» 1978г.
5. «Машинные имитационные эксперименты с моделями экономических систем» под редакцией Нейлера.
6. Бусленко М.П. «Моделирование сложных систем».
7. Кеольтон В., Лод А. «Имитационное моделирование. Классика CS» издание 3-е, 2004г.
Содержание
Введение
Глава1. Моделирование систем массового обслуживания
1.1. Структура и параметры эффективности и качества функционирования СМО
1.2 Классификация СМО и их основные элементы
1.3 Процесс имитационного моделирования
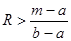Дата: 2019-07-30, просмотров: 248.
