К проблеме дезактивации возбуждений в условиях переноса энергии имеет отношение широкий круг как экспериментальных, так и теоретических вопросов. Квантово – механическая теория переноса энергии в конденси­рованных средах была развита Т. Фёрстером [1,2]. В ней предполагается, что перенос энергии происходит благодаря слабому диполь-дипольному взаимодействию между молекулами. И происходит он в несколько этапов:

1) сообщение энергии молекуле донора с переводом ее в возбужденное состояние;

2) колебательная релаксация возбужденной молекулы донора до установления теплового равновесия со средой или внутренняя конверсия в более устойчивое возбужденное электронное состояние (для органических молекул это нижнее возбужденное синглетное 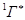 или нижнее триплетное );

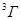3) непосредственная передача возбуждения от донора к акцептору;

4) колебательная релаксация в доноре до установления теплового равновесия со средой и релаксация или внутренняя конверсия в молекуле акцептора;

5) излучение или деградация энергии в акцепторе (при наличии миграции энергии может быть еще передача энергии другой такой же молекуле).

В результате процессов 4 система выходит из резонанса и обратный перенос энергии становится невозможным.

Согласно теории возмущений [21] в квантовой механике вероятность перехода 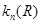системы из начального состояния, описываемого волновой функцией  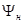в конечное  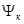определяется выражением:

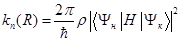                                                                               (1.1)

где 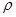 — плотность конечных состояний;  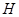— оператор, инициирующий переход (гамильтониан взаимодействия). Для приготовления начального  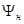и конечного  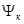квантовых состояний берутся симметризованные определенным образом произведения невозмущенных волновых функций молекул донора и акцептора в соответствующих состояниях 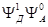, 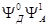. Верхние индексы 0 и 1 отвечают основному и возбужденному состояниям соответственно. В качестве оператора перехода Ферстер берет оператор межмолекулярного взаимодействия. Это положение теории Ферстера, а также выбор начального и конечного электронных состояни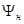й ( и 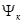) авторы новой теории переноса энергии (В.Я. Артюхов и Г.В Майер) считают ошибочными с позиций современной теории электронных переходов [12,22,23].

В адиабатическом приближении волновые функции 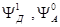,  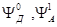записываются через произведение электронной волновой функции  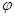на колебательную 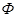. Тогда в одноэлектронном приближении, пренебрегая перекрыванием, имеем

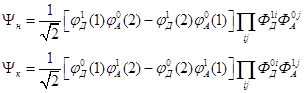
Обозначения (1) и (2) означают координаты первого и второго электронов, а 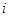 и 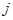 – нормальные колебания в соответствующем состоянии.

Предполагается слабая зависимость электронного матричного элемента от координат ядер молекул (приближение Кондона), который имеет вид

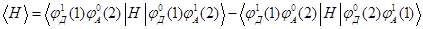       (1.2)

Выражение для вероятности (константа скорости) переноса энергии записывается в следующем виде:

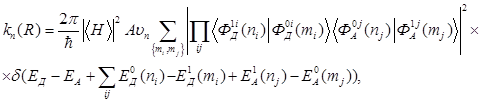(1.3)

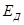где  и 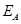 — энергии чисто электронного перехода в доноре и акцепторе соответственно,  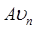означает болцьмановское усреднение по начальному состоянию.

При конкретизации вида гамильтониана взаимодействия 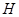, это взаимодействие представляется в виде суммы взаимодействия внешних электронов донора и акцептора. С учетом этого вероятность переноса энергии при диполь-дипольном взаимодействии имеет вид:

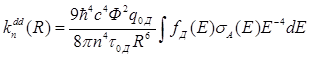,                     (1.4)

здесь 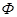 – ориентационный фактор;  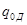и 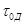 – квантовый выход и время жизни возбужденного состояния донора в отсутствии тушителя;  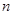– показатель преломления среды на частоте переноса энерги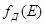и;  и 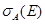 – нормированные спектр излучения донора и сечение поглощения акцептора соответственно.

Таким образом, согласно теории Ферстера, в случае диполь-дипольных взаимодействий вероятность переноса энергии 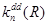 пропорциональна силам осцилляторов переходов в доноре и акцепторе, интегралу перекрытия нормированного спектра излучения донора со спектром поглощения акцептора и обратно пропорциональна шестой степени расстояния между молекулами.

Позже теория Фёрстера была обобщена Декстером на случай мультипольных и обменных взаимодействий [11]. Дальнейшее ее развитие состояло в учете макроскопических параметров, влияющих в основном на константу скорости передачи энергии. При этом считается, что взаимодействие между компонентами донорно – акцепторной пары не влияет на константы скоростей как излучательной, так и безызлучательной дезактивации возбуждений акцептора, поскольку для приготовления начального и конечного квантовых состояний берутся невозмущенные волновые функции изолированных молекул донора и акцептора энергии в соответствующих состояниях. Именно это положение теории Фёрстера – Декстера подвергается критике в Новой теории переноса энергии, разрабатываемой в последнее время В.Я. Артюховым и Г.В. Майером. Перенос энергии за счет обменных взаимодействия становится актуальным, когда кулоновская часть электронного матричного элемента взаимодействия 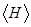 в (1.2) значительно меньше обменной

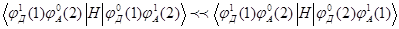.     (1.5)

Неравенство (1.5) выполняется для интеркомбинационных синглет-триплетных переходов в органических молекулах. Поэтому основной вклад в 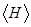 в этом случае дает обменный интеграл. Взаимодействия такого типа названы В.Л. Ермолаевым и А.Н. Терениным обменно-резонансными, и хотя в литературе известны и другие термины, этот термин наиболее широко используется в настоящее время специалистами.

Рассмотрим более подробно межмолекулярный триплет-триплетный перенос энергии электронного возбуждения, происходящий по обменно-резонансному механизму.

Если представить электронные волновые функции донора и акцептора в виде произведения координатной волновой функции 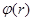 на спиновую 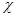, то обменный интеграл  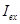имеет вид

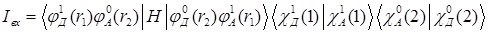. (1.6)

Здесь учтено, что 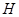 описывает кулоновское взаимодействие, которое не действует на спиновые переменные.

Из (1.6) следует, что обменный интеграл 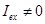, если

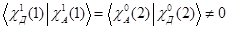
Возбужденное и основное состояния могут иметь разную мультипольность, т. е.

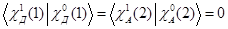                         (1.7)

Следовательно, мультипольность состояний донора и акцептора после акта передачи должна измениться одновременно.

Учитывая, что спектр излучения донора и поглощения акцептора определяются интегралами Франка-Кондона и используя (1.3) Декстер [11] записал выражение для вероятности переноса энергии по обменно-резонансному механизму в следующем виде

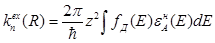                         (1.8)

здесь 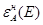 — нормированный спектр поглощения акцептора.

Поскольку величина обменных взаимодействий пропорциональна плотности перекрывания электронных облаков донора и акцептора энергии, которая экспоненциально убывает с расстоянием 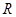 между ними, то параметр 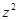, в котором скрыта зависимость  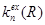от расстояния, можно представить в виде 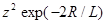, где L — средний эффективный боровский радиус.

Таким образом, Декстер показал, что вероятность переноса энергии 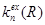 по обменно - резонансному механизму пропорциональна интегралу перекрытия спектра излучения донора со спектром поглощения акцептора, экспоненциально убывает с увеличением расстояния между молекулами акцептора и донора и, в отличие от индуктивно-резонансного механизма, не зависит от сил осцилляторов переходов в доноре и акцепторе.

Установить непосредственную связь 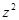 с экспериментально определяемыми параметрами Декстеру не удалось. Позже в работе [24] Инокути и Хирояма провели теоретическое рассмотрение тушения фосфоресценции донора по обменно-резонансному механизму, основываясь на предложенной в [11] экспоненциальной зависимости константы скорости переноса энергии от расстояния между компонентами донорно-акцепторной пары. Обозначив 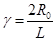, где 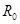 – критический радиус переноса они записали выражение для  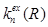в виде

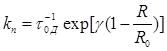.                                  (1.9)

Здесь 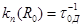, где 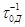 – средняя длительность затухания донора в отсутствии акцептора.

Обобщая основные положения и выводы теории межмолекулярного переноса энергии в конденсированных средах по обменно-резонансному механизму Ферстера-Декстера можно сказать следующее. Взаимодействие между компонентами донорно-акцепторной смеси увеличивает константу скорости безызлучательной дезактивации триплетных возбуждений в молекулах донора только за счет передачи энергии акцептору. Константы скоростей излучательной дезактивации триплетных молекул донора и триплетных молекул акцептора, а также константа скорости безызлучательной дезактивации триплетных молекул акцептора при этом должны оставаться такими же каковыми они были в однокомпонентных растворах.

Следствием этого должно быть отсутствие влияния донора на время затухания фосфоресценции акцептора и независимость квантового выхода сенсибилизированной фосфоресценции от концентрации раствора. Следует заметить, что под квантовым выходом сенсибилизированной фосфоресценции имеется ввиду, здесь и в дальнейшем, отношение числа квантов излучаемых акцептором к числу потушенных триплетных молекул донора за это же время в результате передачи энергии [25] (по определению В.Л. Ермолаева и А.Н. Теренина). Отношение же числа излученных квантов акцептором в единицу времени к числу поглощаемых квантов света донором за это же время будем называть абсолютным квантовым выходом сенсибилизированной фосфоресценции, как и в [25].

Последовательный критический анализ теории Ферстера для описания переноса энергии с позиций современной теории безызлучательных переходов был проведен В.Я. Артюховым и Г.В. Майером в [12]. Показано, что основные положения теории Ферстера ошибочны с точки зрения современной теории электронных переходов [12,13,26,27]. Так же установлены некоторые противоречия между выводами теории и экспериментальными фактами. При исследовании бихромофорных систем, содержащих ароматические молекулы, так же установлено, что величина ориентационного фактора в теории Ферстера часто не согласуется с экспериментальными данными по переносу энергии при строго определенной относительной ориентации молекул донора и акцептора.

Согласно [12,13] волновые функции и оператор, инициирующий перенос электронной энергии, в теории Ферстера определены неправильно. Волновые функции в выражении (1.1) и начального и конечного состояний описывают возбужденные электронные состояния бимолекулярной системы. Если оператор не содержит спиновых переменных, то возможен переход только между состояниями одинаковой мультиплетности. Оператор 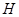 в (1.1) по Ферстеру не зависит от спиновых переменных и поэтому не может инициировать, согласно [12,13], электронный переход (перенос энергии).

Наиболее прост для рассмотрения предложенной теории случай синглет-синглетного переноса энергии при большом расстоянии между молекулами. При пренеб­режении взаимодействием между молекулами (в выражении для полного электронного гамильтониана бихроморфной системы 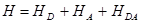 (1.10), здесь 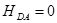) для любого состояния системы волновая функция имеет вид прямого произведения волновых функций молекул

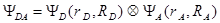                                                            (1.11)

Все состояния этой системы соответствуют невозмущенной системе в теории возмущений. С физиче­ской точки зрения такая ситуация соответствует полной изолированности подсистем общей системы, т. е. набор состояний системы является просто суммой состояний подсистем. Все свойства полной системы (в том числе и спектрально-люминесцентные) будут аддитивны по отношению к аналогичным свойствам подсистем. Перенос энергии электронного возбуждения в такой системе может происходить только за счет реабсорбции излучения донора молекулой акцептора. Здесь волновые функции молекул есть прямые произведения электронной, колебательной и спиновой функций. Учет межмолекулярного взаимодействия ( 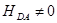) изменяет гамильтониан только электронной задачи, так как оператор  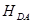не со­держит взаимодействий, которые включают неадиабатичность или смешивание спиновых состояний. С точки зрения квантовой теории общая электронная волновая функция системы в этом случае не может быть представлена в виде (1.11). Возникают новые состояния системы с электронными функциями 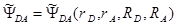. Однако квантово-химические расчеты показывают, что можно по-прежнему классифицировать состояния системы как набор возмущенных состояний подсистем:

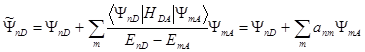                             (1.12)

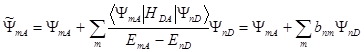                              (1.13)

Это же показывают и экспериментальные спектры поглощения бимолекулярных систем [12,14,15]. Обычно их ин­терпретируют как почти аддитивные. Нарушение аддитивности свойств системы существенно зависит от величин 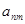и 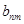 т. е. от величины межмолекулярного взаимодействия молекул D и А в соответствующих электронных состояниях и энергетического интервала между ними. Для осуществления процесса переноса энергии принципиально важно, что волновые функции электронных состояний бимолекулярной системы теряют строгую пространственную локализацию и, в общем случае, делокализованы по всей системе. Именно пространственная делокализация электронных волно­вых функций состояний компонент бимолекулярной системы является необходимым условием осуществ­ления в ней межмолекулярных фотофизических процессов.

Авторы [12,14,15] указывают на еще одну принципиальную ошибку исследования процесса переноса энергии согласно тео­рии Ферстера (в том числе при классическом рассмотрении). Предполагается, что межмолекулярное взаи­модействие молекул D и А включается после возбуждения системы, т. е. возбуждаются невозмущенные состояния (1.11). В действительности возбуждаются возмущенные состояния (1.12) и (1.13), а не состояния (1.11). Возмущение в виде межмолекулярного взаимодействия возникает сразу после синтезирования молекулы бихромофора или приготовления бимолекулярного раствора. Это отчетливо регистрируется в спектрах молекул. В таком подходе предлагаемая модель системы полностью соответствует исходным предполо­жениям теории электронных переходов (в том числе процедуре приготовления возбужденного состояния), и дальнейшее исследование фотофизики бимолекулярной системы может быть проведено в рамках этой теории. Так же В.Я. Артюхов и Г.В. Майер отмечают, что в принципиальном плане любой электронный переход между электронно-колебательными состояниями системы сопровождается переносом энергии и является резонансным с точ­ки зрения закона сохранения энергии системы.

Далее, в отличии от модели Ферстера при описании переноса энергии, здесь используется модель, рассматривающая перенос энергии, как процесс внутренней конверсии в бихромофорной или бимолекулярной системе. Для расчетов констант скоростей переходов и энергии в бимолекулярной системе применяется модель «супермолекулы» [12]. В такой модели многокомпонентная молекулярная система рассматривается как единая молекулярная система без разделения ее на отдельные фрагменты. Взаимодействие фрагментов непосредственно учитывается в гамильтониане молекулярной системы. В результате обычного квантово-химического расчета получается набор синглетных и триплетных состояний такой системы. Важно, что в состав «супермолекулы» может войти и растворитель. После расчета энергий и волновых функций электронных состояний, проводится оценка констант скоростей фотофизических процессов: константы скорости излучения, константы скоростей внутренней и интеркомбинационной конверсии. Константа скорости интеркомбинационной конверсии определяется на основе расчетов матричных элементов оператора спин-орбитального взаимодействия. Начальное и конечное состояния системы, между которыми происходит перенос энергии (внутренняя или интеркомбинационная конверсия), являются возмущенными состояниями системы. Возмущение состояний системы за счет межмолекулярного взаимодействия компонент не вызывает электронного перехода, но является необходимым условием осуществления таких переходов между состояниями, локализованными преимущественно на разных компонентах. Электронный переход инициируется традиционными для фотофизических процессов возмущениями: неадиабатичностью и спин-орбитальным взаимодействием [28].

Теорию переноса энергии основанную на квантово-химической модели В.Я. Артюхов и Г.В. Майер назвали новой теорией переноса энергии [12,23]. Авторы [12,23] указывают на следующие причины, по которым теория Ферстера удовлетворительно объясняет перенос энергии между органическими молекулами.

1) Теория Ферстера-Декстера правильно формулирует основную зависимость скорости переноса энергии 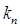 для обоих типов передачи энергии.

2) Зависимость вероятности переноса от разности энергетических уровней донора энергии 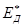 и акцептора энергии  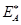в новой теории близка к аналогичной зависимости  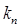от интеграла перекрывания спектров излучения молекул донора и поглощения молекул акцептора в теории Ферстера.

3) Правила отбора для радиационных переходов (которыми модулируется перенос энергии в теории Ферстера) и внутренней конверсии по отношению к орбитальной природе и симметрии волновых функций начального и конечного состояний системы одинаковы [14].

Поскольку вероятность переноса энергии, согласно новой теории, зависит от разности энергий ( 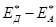), то должна быть ее зависимость от частоты перехода в пределах неоднородно уширенной полосы  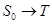перехода в акцепторе. В теории Ферстера она менее ярко выражена.

Таким образом, согласно новой теории переноса энергии, можно ожидать изменения константы скорости излучательного перехода триплетных молекул акцептора в основное состояние, обусловленное взаимодействием между молекулой донора в основном состоянии и молекулой акцептора в триплетном состоянии. Так же можно ожидать зависимости константы скорости перехода молекул акцептора из основного состояния в триплетное в результате передачи им энергии от частоты перехода в пределах неоднородно уширенной 0 - 0 полосы.