Билет 1. Материальная точка. Абсолютно твердое тело. Система отсчета. Закон движения материальной точки. Вектор перемещения. Путь. Скорость и ускорение.
Материальная точка- это тело, размера тела которого можно пренебречь в условиях данной задачи.
АТТ- если расстояние между двумя точка тела неизменно, то такое тело называется абсолютно твердое тело.
Система отсчета- система координат, связанная с телом отсчета и система отсчета времени
Тело отсчета- АТТ относительно которого задается положение других тел.
Способы задания положения тела в пространстве: векторное, координатное
|
|
Закон движения материальной точки- уравнение или система уравнений, определяющих положение тела в любой момент времени относительно выбранной системы отсчета.
Векторный способ-
- 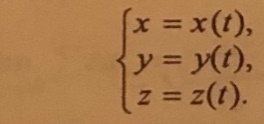
Векторное перемещение- вектор, проведенный из начального положения точки в конечное называется в.п.
Путь- расстояние, между точками 1 и 2, измеряемое вдоль траектории. 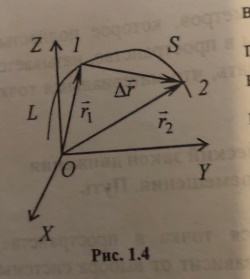
Скорость и ускорение-
Скорость- векторная величина характеризующая быстрое перемещение движения материальной точки относительно выбранной системы отсчета.
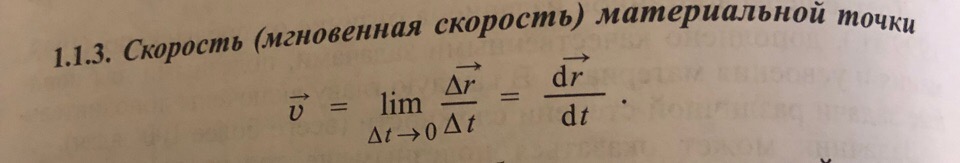
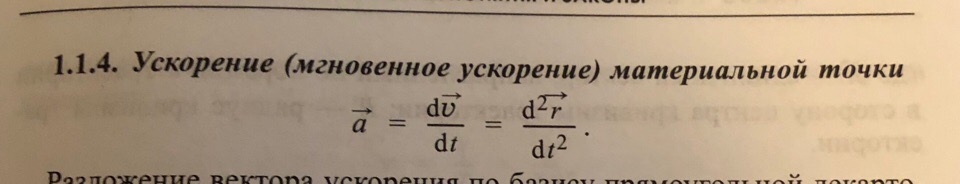
Билет 2. Вектор ускорения. Закон движения тела в случае постоянного ускорения. Нормальное и тангенциальное ускорение.
.


Билет 7. Энергия. Различные формы энергии. Потенциальная энергия. Изменение потенциальной энергии. Потенциальная энергия гравитационного взаимодействия и упругой деформации.
Потенциальная энергия- физическая величина, изменение которой равно работе потенциальной силы, взятой со знаком минус. Минус показывает, что если потенциальная сила совершает положительную работу, то потенциальная энергия при этом уменьшается.
dWn=-бA(Fn)
Потенциальная энергия есть функция взаимодействия между телами.
Потенциальная энергия функции взаимодействия двух тел с массой m1 и m2 : Wn= -Gm1*m2/R
Потенциальная энергия упругой деформации: A= (интеграл)dA=(интеграл от x2 до x1) - kxdx (kx2/2)-(kx2/2)
Wn=kx2/2
Билет 8. Потенциальная энергия. Связь между силой и потенциальной энергией. Градиент скалярного поля.
Потенциальная энергия- физическая величина, изменение которой равно работе потенциальной силы, взятой со знаком минус. Минус показывает, что если потенциальная сила совершает положительную работу, то потенциальная энергия при этом уменьшается.
dWn=-бA(Fn)
Связь между силой и потенциальной энергией.
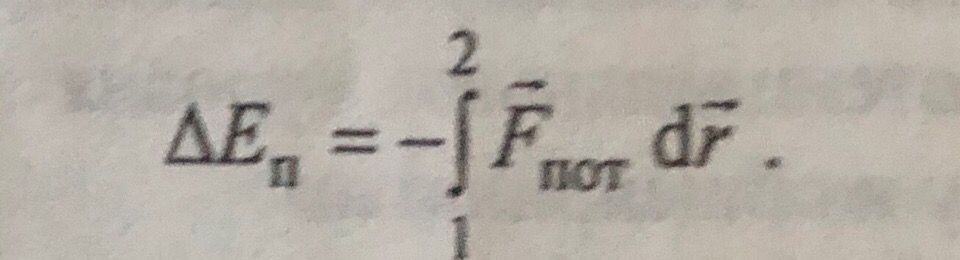
Градиент скалярного поля
Потенциальная энергия есть функция взаимодействия между телами.
F=grad Wn – Сила направленна в сторону убыли потенциальной энергии.
Билет 9. Кинетическая энергия. Теорема об изменении кинетической энергии. Кинетическая энергия системы материальных точек. Закон сохранения механической энергии. Пример использования закона сохранения механической энергии.
Кинетическая энергия- энергия механической системы, зависящая от скоростей ее точек. Кинетическая энергия механической системы равна сумме кинетических энергий всех ее точек.
Wk= mu2/2
Теорема об изменении кинетической энергии- изменение кинетической энергии системы при ее перемещении из положения 1 в положение 2 равна сумме работ внешних и внутренних сил, под действием которых происходит это перемещение. (дельта)Wk=Wk2-Wk1= Aвнеш.+Aвнутр.
Кинетическая энергия системы материальных точек- складывается из кинетической энергии точек и тел, входящих в систему.
Закон сохранения механической энергии- механическая энергия сохраняется если суммарная работа внутренних и внешних сил равна нулю.
Пример использования закона сохранения механической энергии- этот закон применяется в абсолютно упругом и абсолютно не упругом ударе.
Абсолютно упругий удар- механическая энергия системы не изменяется.
m1u1+m2u2=m1u1’ +m2u2’
Абсолютно неупругий удар- механическая энергия системы не изменяется.
m1u1+m2u2= (m1 +m2 )u’
Билет 10. Кинематические характеристики вращательного движения (угловое перемещение, угловая скорость и угловое ускорение), их связь с линейными характеристиками движения точек тела.



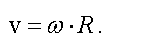
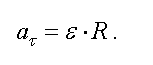
ВОПРОС 12 Момент инерции материальной точки и АТТ. Примеры расчета момента инерции. Уравнение Гюйгенса-Штейнера
Расчет момента инерции тонкого однородного стержня относительно оси проходящий через его центр и перпендикулярный плоскости 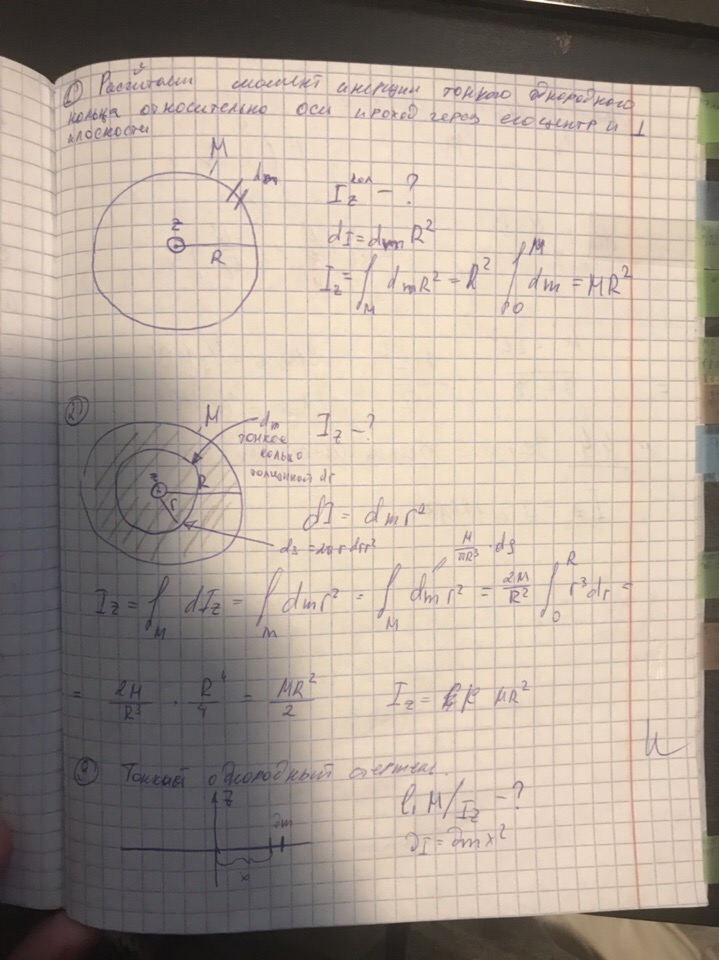

Вопрос 16 Механические колебания. Гармонические колебания. Примеры свободных колебаний.
Механические колебания – состояние физической системы для которого характерно определенное повторяемость во времени физических величин, определяющих состояние с-мы.
Колебание называется периодическим, если значения физических величин определяющих состояние систем, повторяются через равные промежутки времени
Кинематика гармонических колебаний
Гармонические колебания – процесс в котором физические величины изменяются по гармоническому закону

Xm – амплитуда
w- частота колебаний
q – начальная фаза колебаний 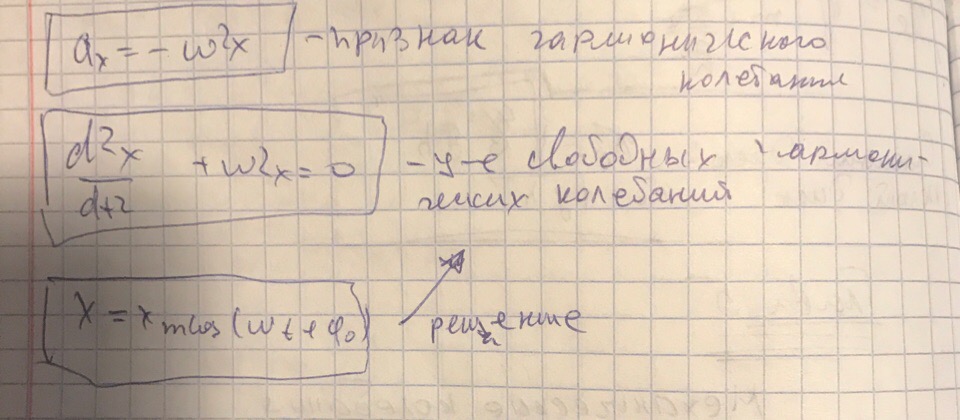
Пружинный маятник: a=-(k*x)/m
Математический маятник 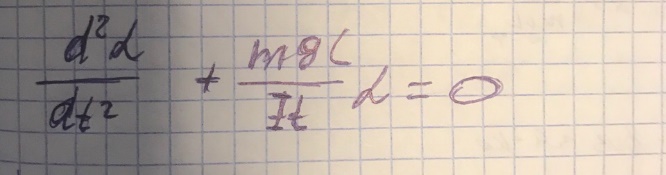
Вопрос 17 Свободные гармонические колебания на примере физ маятника. Мех энергия гармонических колебаний.
Физический маятник
Это некоторое тело (АТТ), совершающее колебания под действием силы тяжести, относительно оси, и не проходящий через центр масс оси
Т. О – точка подвеса
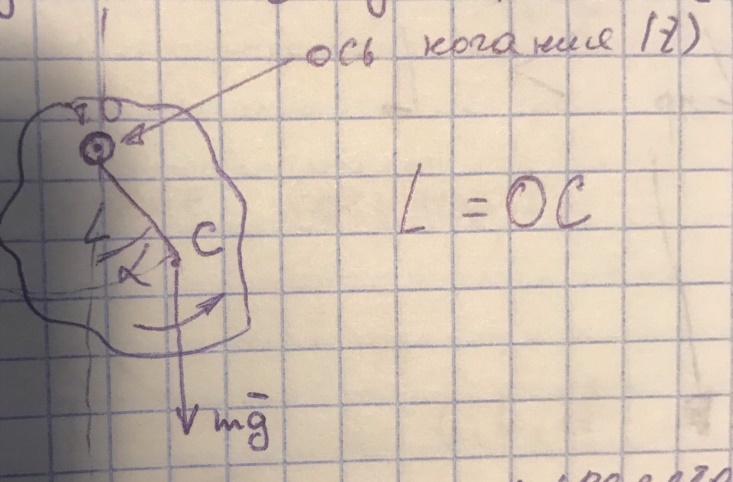
Т. о получается через пересечение, проходящих через центр масс.

Вопрос 20
ВОПРОС 21
ВОПРОС 22
Функции распределения Максвелла молекул газа по модулям скоростей. Наиболее вероятная, средняя и средняя квадратичная скорости молекул. Зависимость функции распределения молекул газа по модулям скоростей от температуры.
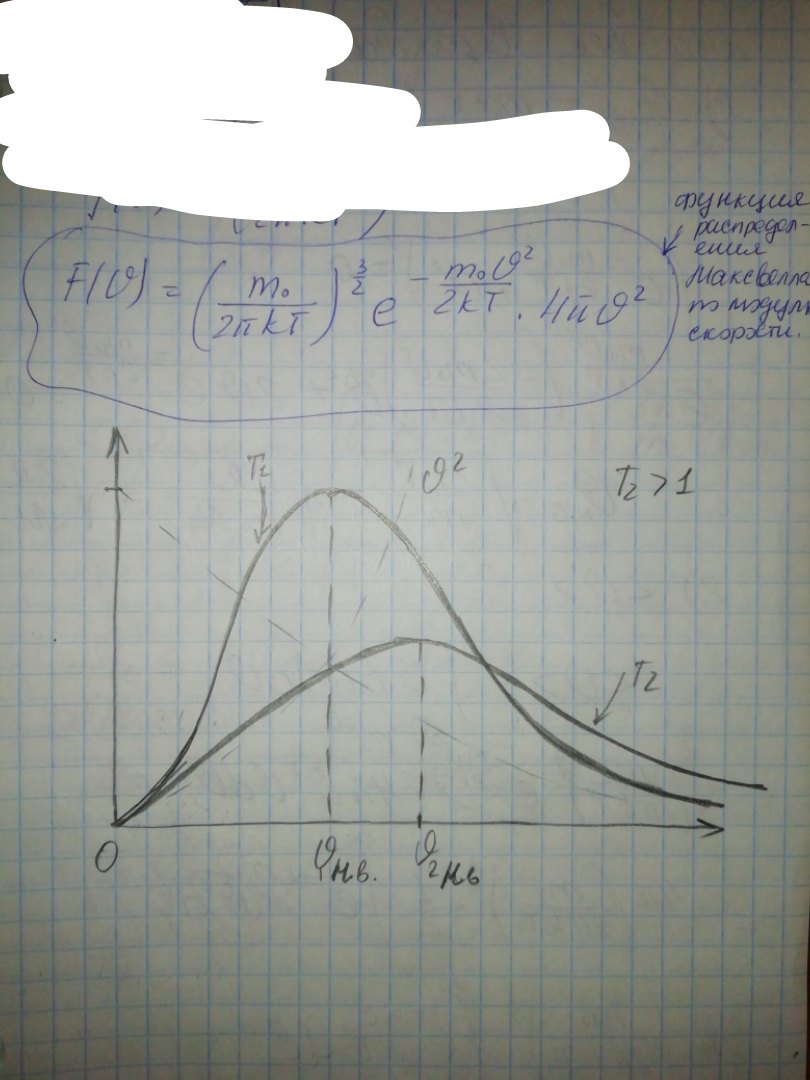
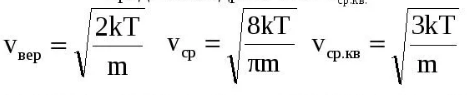
26. Распределение Больцмана (барометрическая формула).
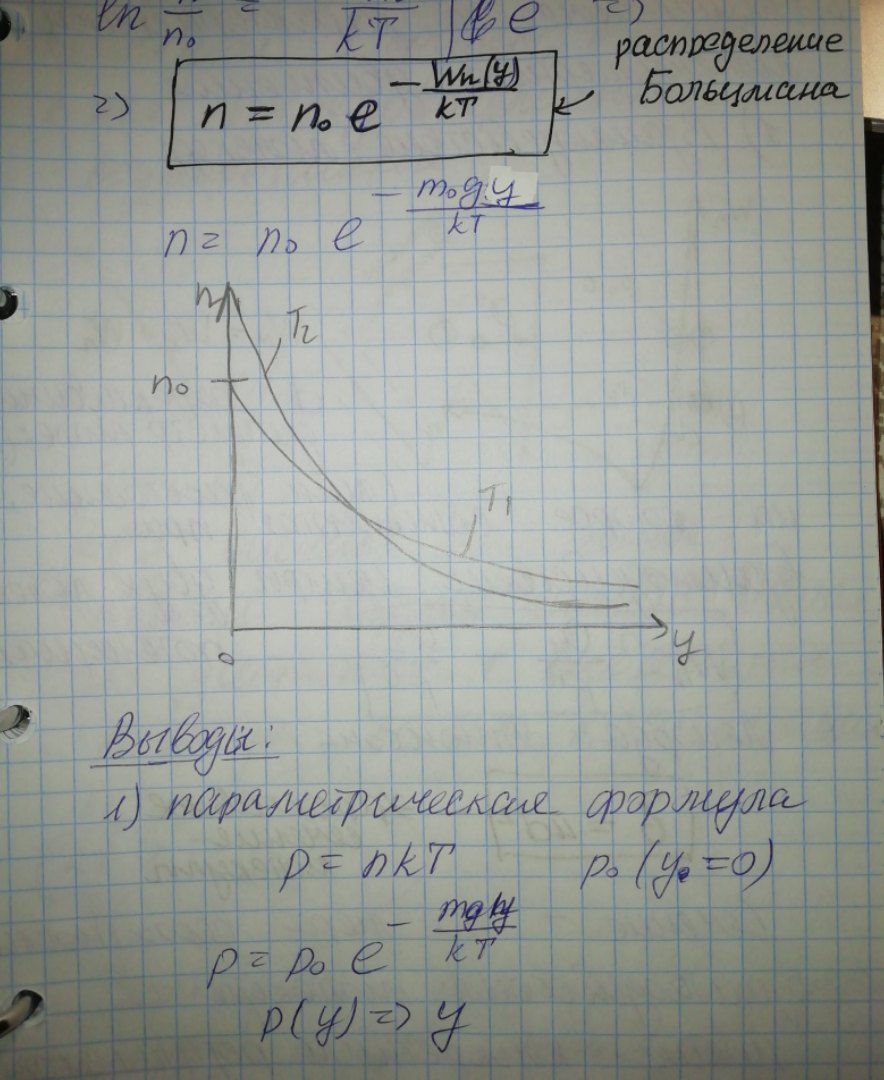
Понятие эффективного диаметра молекулы и эффективного сечения процесса столкновений. Среднее число столкновений одной молекулы газа в единицу времени. Средняя длина свободного пробега молекулы и ее зависимость от давления и температуры.
Эффективный диаметр молекулы - среднее расстояние между центрами молекул, на которое две молекулы сближаются при их столкновении.
Эффективное сечение столкновения - площадь поперечного сечения “коридора”, в который должны попасть центры соседних молекул, чтобы столкнуться с данной. 𝑆эфф=𝜋𝐷2эфф=4𝜋𝑅2
Среднее число столкновений одной молекулы газа в единицу времени.𝑁=𝑛〈𝑣〉𝑆эфф Средняя длина свободного пробега – расстояние, которое она пролетает между двумя последовательными соударениями.〈𝑙〉=〈𝑣〉𝜏=1/𝑛𝑆эфф ; 〈𝑙〉=𝑘𝑇/ 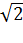 *4𝑝𝑅𝜋
*4𝑝𝑅𝜋
Билет 1. Материальная точка. Абсолютно твердое тело. Система отсчета. Закон движения материальной точки. Вектор перемещения. Путь. Скорость и ускорение.
Материальная точка- это тело, размера тела которого можно пренебречь в условиях данной задачи.
АТТ- если расстояние между двумя точка тела неизменно, то такое тело называется абсолютно твердое тело.
Система отсчета- система координат, связанная с телом отсчета и система отсчета времени
Тело отсчета- АТТ относительно которого задается положение других тел.
Способы задания положения тела в пространстве: векторное, координатное
|
|
Закон движения материальной точки- уравнение или система уравнений, определяющих положение тела в любой момент времени относительно выбранной системы отсчета.
Векторный способ-
- 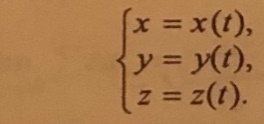
Векторное перемещение- вектор, проведенный из начального положения точки в конечное называется в.п.
Путь- расстояние, между точками 1 и 2, измеряемое вдоль траектории. 
Скорость и ускорение-
Скорость- векторная величина характеризующая быстрое перемещение движения материальной точки относительно выбранной системы отсчета.
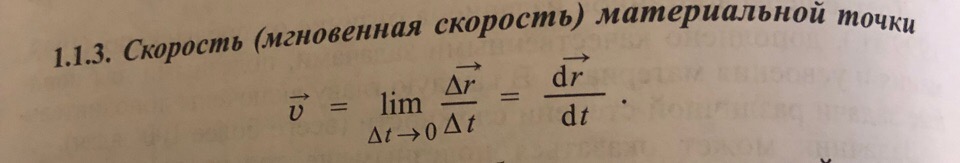
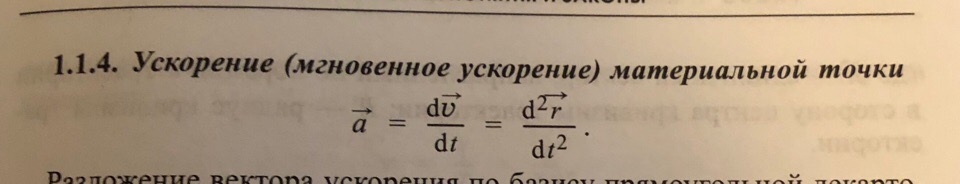
Дата: 2019-07-30, просмотров: 407.