Любое внешнее воздействие на твердое тело сопровождается генерированием и распространением в нем упругих волн. Распространяющиеся волны передают информацию об имевшем место внешнем воздействии от точки к точке в теле.

Динамическим считается такое нагружение, при котором частицы деформируемой среды получают ускорение, и в теле возникают силы инерции. Строго говоря, все виды нагружения следует считать динамическими. На практике же исследователи всегда стремятся провести границу между этими двумя видами приложения нагрузки. В конечном итоге, все определяется скоростью приложения нагрузки, длительностью нагружения.

При кратковременном воздействии малой интенсивности наблюда-ется динамическая волновая картина, которая складывается из прямых и отраженных от любых (как внешних, так и внутренних) границ тела волн. Воздействие большой интенсивности приведет к образованию поверхностей разрыва, в теле распространяется ударная волна упруго-пластической нагрузки. Во всех случаях определяющее значение в процессе деформирования имеют волновые процессы.

Напряженно-деформированое состояние, возникающее в образце горной породы при динамическом воздействии, существенно отличается от напряженно-деформированного состояния, возникающего при статическом нагружении такого же образца: если при статическом нагружении образца (при сжатии, например) весь объем образца подвержен действию сжимающей нагрузки, то главной особенностью напряженно-деформированого состояния, возникающего при скоростном взаимодействии двух тел, является неравномерность распределения напряженного состояния во времени и по величине в образце.

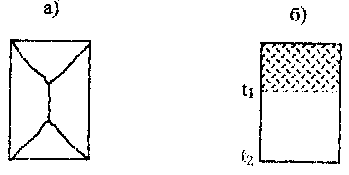
Рассмотрим качественную картину деформирования образца при статическом и динамическом приложении нагрузок (рис. 27). При динамическом нагружении верхнего торца образца в нем возникает волна сжатия, распространяющаяся по образцу со скоростью звука в данном теле. В зависимости от продолжительности Δt действия силы F в образце может возникнуть следующее напряженное состояние: в момент времени t₁ верхняя часть образца будет сжата, а остальная часть образца – свободна от напряжений. При достижении противоположной поверхности образца в момент времени t₂ весь образец может быть сжат. Отразившись от этой поверхности, волна сжатия превращается в волну разгрузки – волну растяжения.

В результате, при динамическом нагружении образца в теле образуется резко неоднородное поле напряжений, возникают большие градиенты напряжений и деформаций. Разрушение в таком поле напряжений происходит во всем объёме образца. Если еще вспомнить, что горная порода есть гетерогенное образование с большим количеством пор и трещин, адгезионных границ раздела между минералами, между минералами и цементирующим веществом, то станет понятно, что возникновение волн отражения будет происходить на всех границах раздела во всём объёме образца. Этот процесс приведёт к разупрочнению всего образца горной породы, а при большой скорости соударения и к его распаду на мелкие части.

При большой энергии соударения может произойти разрушение на контакте соударяющихся тел: возможно наблюдение откольных явлений при достижении волной сжатия торцовой поверхности образца.

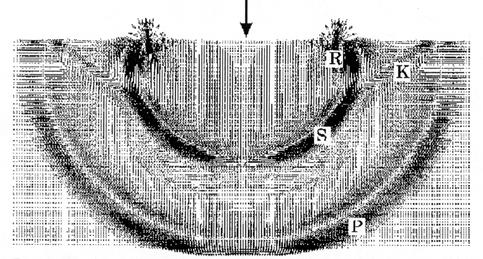
6.1.1. Локальное импульсное механическое воздействие на поверхность твердого тела. Участок поверхности упругого однородного и изотропного полупространства подвергается кратковременному действию вертикальной нагрузки (рис. 28). В теле на некотором расстоянии от источника возмущения формируется продольная волна растяжения-сжатия P и поперечная волна сдвига S. Разделение типов волн происходит по ориентации движения частиц на их фронтах: во фронте продольной волны движение частиц происходит по направлению ее распространения, а во фронте поперечной волны частицы двигаются перпендикулярно направлению ее распространения.

Продольные и поперечные волны распространяются с различными скоростями. Скорость продольной волны определяется соотношением                      

V_p² = (K+4G/3)/r = E/r,

поперечной

V_s² = G/r,

где K – модуль объемного сжатия, G – модуль сдвига, r – плотность материала полупространства.

Наличие поверхности раздела (граница полупространства является свободной поверхностью) приводит к появлению конических и поверхностных волн. Коническая волна К является огибающей сдвиговых волн, возникших в результате взаимодействия продольной волны со свободной поверхностью. Она соединяет фронты продольной и поперечной волн, ее фронт тянется от места выхода продольной волны на поверхность по касательной к фронту поперечной волны. Различие в направлениях смещений приводит к вихревому движению частиц между фронтами конической и поперечной волн. Вблизи свободной поверхности, чуть отставая от поперечной, движется поверхностная волна Рэлея R, которая быстро затухает с глубиной, но вызывает разрушение поверхностного слоя.

В случае статического приложения нагрузки волновые процессы возникают лишь в первые моменты нагружения и затем затухают и не влияют на процесс образования напряжений: во всем образце горной породы возникают напряжения сжатия. Как мы уже знаем, разрушение образца в случае статического приложения нагрузки имеет конусную форму и начинается в местах достижения касательными напряжениями предела прочности породы на сдвиг (рис. 27а).

Когда упругая энергия, запасенная в статически сжатом образце горной породы, достигает больших значений, возможна реализация динамического разрушения образца при мгновенном снятии нагрузки c образца. Образец горной породы при этом может разрушиться на мелкие куски (самоподдерживающееся разрушение).

Динамические методы определения деформационных характеристик горных пород основаны на возбуждении в породе волновых колебаний и определении скорости распространения в ней упругих волн (продольных, поперечных).

При динамических нагрузках наблюдаются более высокие значения параметров упругости, прочности, твердости.

6.1.2. Показатели динамических свойств горных пород. К показателям динамических свойств горных пород относят следующие:

1. Акустическая жесткость A =  r _п V_p, dim A = кг·с^-1·м^-2. Эта величина характеризует сопротивление горной породы распространению упругой продольной волны.

2. Динамический модуль упругости E_д = V_p²r _п .

Величина E_д превышает модуль Юнга E, определяемый в статических испытаниях, в 1,1 – 1,7 раза. Это объясняется тем, что при статическом нагружении значительнее проявляются процессы неупругого деформирования, приводящие к снижению величины модуля Юнга. Максимальные различия между E_д и E наблюдаются у пористых горных пород.

Величина модуля деформации E_деф, модуля Юнга E и динамического модуля упругости E_д образуют ряд:

E_д > E > E_деф.

3. Динамический коэффициент Пуассона определяется отношением

n_д = (0.5 – R²) / (1 – R²),

где R = V_s / V_p < 1 (V_p > V_s в 1,7 – 2,4 раза). Величина n _д меньше значения коэффициента Пуассона n _с (11), измеренного статическим методом. У доломитов и известняков, например, n _д   меньше n _с  в 1,7 – 2,1 раза.

4. Динамический модуль сдвига G_д = V_s²r _п.

5. Динамический модуль объемной упругости (объемного сжатия)

K = E_д / [ 3 (1 – n_д) ].

6. Динамическая твердость горных пород H_д. Этот показатель определяется с помощью приборов Шора и В.П.Шубина.

В методике Шора определения твердости на поверхность закрепленного испытываемого образца горной породы толщиной 40 мм сбрасывается с постоянной высоты боек с алмазным сферическим наконечником. Образцы горной породы должны иметь две поверхности параллельными и шлифованными. Верхняя поверхность образца подвергается воздействию бойка с наконечником. Средняя высота отскока бойка после многократных сбрасываний в разные точки торцовой поверхности образца характеризует твердость образца горной породы. Отношение высоты отскока к высоте сбрасывания называется коэффициентом отскока, который характеризует упругие свойства горной породы.

В методе В.П.Шубина сбрасываемый боек, изготовленный из закаленной стали, имеет форму конуса с углом при вершине 90⁰. Показатель динамической твердости определяется по формуле

H_д = Gh / V_л,

где G – вес бойка, h – высота сбрасывания бойка, V_л – объем возникшей лунки на торцовой поверхности образца. Диаметр лунки измеряется под микроскопом с точностью 5×10^-6 м.

Применение динамических методов для определения свойств горных пород позволяет исследовать свойства пород как в образце, так и в условиях естественного залегания горных пород.

 6.1.3. Формы разрушения. Разрушение горной породы при её динамическом нагружении описывается с помощью кинетической энергии движущегося породоразрушающего инструмента

W_k = mV² / 2

и потенциальной энергии деформирования горной породы

      d_max

U =  ò f(d)dd,

                ⁰

где V – скорость соударения инструмента с горной породой, m – масса инструмента, d _max – максимальная глубина проникновения породоразрушающего элемента вооружения долота в горную породу, f(d) – сила сопротивления горной породы внедрению породоразрушающего элемента вооружения долота.

Условие

W_k = U

является основным при анализе ударного взаимодействия инструмента с горной породой.

Вид функции f(d) зависит как от физико-механических свойств горных пород, так и от геометрии породоразрушающего инструмента. Общий вид функции f(d) к настоящему времени не определен, и это затрудняет проведение математического анализа разрушения горных пород при динамическом нагружении. По этой причине единственным методом исследования процесса разрушения при динамическом нагружении является эксперимент.

Эксперимент показывает, что с увеличением кинетической энергии движущегося тела (использовался ударник цилиндрической формы с плоским основанием) картина разрушения поверхности горной породы качественно выглядит следующим образом. Увеличение скорости соударения вначале приводит лишь к небольшому углублению ударника в поверхность породы: на поверхности образца горной породы виден след ударника в виде остаточной деформации. Под пятном контакта и около него возникает сеть трещин, которая с увеличением скорости соударения становится все гуще.

При определенном значении кинетической энергии W ₂ (рис. 29) происходит круговой выкол породы в области, окружающей пятно контакта. Этот вид разрушения называют первой формой разрушения при динамическом нагружении. Основной особенностью первой формы разрушения является резкий рост объема разрушенной горной породы.

С дальнейшим увеличением скорости соударения основной прирост объёма разрушенной породы обеспечивается постепенным внедрением ударника в горную породу. При достижении кинетической энергией значения W ₄ наступает вторая форма разрушения: объем разрушенной породы вновь резко возрастает вследствие образования лунки под пятном контакта.

Предполагается, что с дальнейшим ростом кинетической энергии будут наблюдаться и последующие формы разрушения.

Изменение энергоёмкости разрушения. Немонотонное изменение объема горной породы при увеличении скорости соударения определяет и аналогичное изменение удельной объёмной энергоемкости разрушения А_v = W_к / V при динамическом нагружении (рис.29).

Минимальные значения энергоёмкости соответствуют скачкам разрушения горной породы, т.е. тем значениям энергии W_к, при которых она полностью идет на разрушение. При изменении энергоемкости наблюдается следующая закономерность: каждый следующий минимум энергоёмкости А_v меньше предыдущего. При увеличении энергии удара от W₂ до W₃, от W₄ до W₅ и т.д. (рис. 29) энергия удара расходуется на упругие деформации горной породы, уплотнение породы и образование в ней зоны предразрушения.

В горной породе под внедрившимся элементом породоразрушающего инструмента выделяют следующие зоны разрушения (рис. 30). В области 1 кроме разрыва адгезионных связей между минералами происходит и разрушение самих минералов.

Подобный способ разрушения хорош для упругохрупких горных пород. Его можно использовать и для разбуривания упругопластических пород. Но необходимо помнить следующее: для эффективного дробления таких горных пород необходимо повышать скорость соударения, т.к. в этом случае горная порода будет проявлять в меньшей степени свои пластические свойства

6.1.4. Природа динамического действия шарошечного долота. Динамическое воздействие по горной породе забоя скважины реализуется при использованиии любых долот. Исключительно за счет ударной нагрузки разрушаются горные породы при использовании долот дробящего действия. Но для нанесения удара по горной породе забоя скважины вовсе не обязательно использовать долота дробящего действия. Шарошечное долото наносит удары по горной породе забоя скважины при перекатывании шарошки с зуба на зуб, за счет накопления упругой энергии в бурильной колонне и неоднородности горных пород.

Дробящая способность шарошечного долота обеспечивается перекатыванием шарошек по забою с зуба на зуб. Это обеспечивает вертикальное перемещение не только долота, но и всей бурильной колонны. По этой причине на горную породу забоя действует динамическая нагрузка F _д во время удара зуба долота по забою, а затем и статическая нагрузка F _ст, обеспечивающая дальнейшее внедрение зуба в поверхность забоя. Суммарная нагрузка на забой F _S = F _д + F _ст, отнесенная к величине статической нагрузки, определяет коэффициент динамичности:

k = F_S /  F_ст.

Коэффициент динамичности возрастает с увеличением твердости горной породы, шага зубьев и частоты вращения долота. При разбуривании мягких, средних и твердых горных пород величина коэффициента динамичности принимает следующие значения: 1.1, 1.2, 1.3, соответственно.

Эффективность разрушения горной породы на забое скважины под действием усилий F _д , F _ст снижается с возрастанием пластических свойств горных пород. Разрушение горных пород на забое глубоких скважин инструментом, вызывающим дробление, обеспечивает малую величину механической скорости.

Под действием ударной нагрузки, превышающей сопротивление горной породы ударному разрушению, происходит ее дробление и образование лунки в результате выкола породы.

И в состоянии устойчивого и неустойчивого положения шарошки под торцом зуба в горной породе возникает напряженное состояние сжатия. Напряжения сжатия в породе достигнет большей величины при опоре шарошки на один зубец. Если при этом возникающие контактные давления превысят сопротивление породы вдавливанию (P_к > H), то горная порода под пятном контакта разрушится, возникнет лунка.

Перекатывание шарошки по забою с зуба на зуб не является единственной причиной появления динамической нагрузки. Так как нагружаемая горная порода забоя скважины практически всегда неоднородна и в каждый момент времени зубья долота находятся в контакте с забоем в разных сочетаниях, то все это приводит к неравномерному разрушению горной породы. При этом возникают колебания с более низкой частотой, но с большей амплитудой, чем при перекатывании шарошки с зуба на зуб.

При работе шарошечного долота различают следующие колебательные процессы, обеспечивающие динамическое воздействие на забой:

а) высокочастотные, появление которых вызвано зубчатостью шарошек,

б) среднечастотные, природа которых связана с изменением во времени числа взаимодействующих с поверхностью забоя скважины зубьев долота,

в) низкочастотные, обусловленные возникновением вследствие неоднородности строения горных пород и их дефектности ухабов на забое скважины.

6.1.5. Природа динамического действия лопастного долота. Лопастные долота также наносят удар по забою в результате накопления упругой энергии в бурильной колонне. В бурильной колонне, являющейся упругим элементом большой протяженности, возникают продольные, крутильные и поперечные колебания.

Виновником возникновения ударной нагрузки является неоднородность свойств горной породы и использование нежесткой бурильной колонны (системы нагружения): в бурильной колонне при бурении накапливается упругая энергия. Через жесткость бурильной колонны упругую энергию, запасенную в ней, можно представить в виде:

W = D_f ·j² + D_l ·d²,

где D_l – продольная жесткость, d – величина абсолютной упругой деформации, D_f = M_д / j - угловая жесткость, j - угол закручивания бурильной колонны.

Колебания жесткости в процессе бурения приведут не только к изменению энергии W, но и к изменению углубления долота в горную породу.

Изменение осевой нагрузки на долото, происходящее вследствие возникновения продольных колебаний, может составлять 25 ÷ 50 % и более от величины её среднего значения. Продольные (вертикальные) колебания долота с амплитудой, равной 55 мм, являются обычными. Эти колебания приводят к большим динамическим нагрузкам и являются причиной усталостных поломок элементов бурильной колонны. При прочих равных условиях динамичность будет тем меньше, чем больше число лопастей у долота. На возникновение продольных колебаний значительное влияние оказывает неоднородность прочностных свойств горных пород забоя, наличие трещинноватости в породах.

Под крутильными колебаниями понимают изменение угловой скорости около среднего значения, а под поперечными колебаниями понимают периодические перемещение оси долота по забою.

Природа возникновения крутильных и поперечных колебаний одинакова: неравномерная подача долота и неоднородность механических свойств горных пород забоя, приводящие к неравномерному разрушению породы перед лопастями долота (при одинаковой величине запасенной упругой энергии в бурильной колонне). Это приводит к возникновению крутильных ударов (резкое увеличение момента на долоте) и дополнительному закручиванию бурильной колонны на угол j ₁ . При последующем уменьшении подачи происходит уменьшение момента на долоте, при этом буровая колонна раскручивается на угол:

          j₂ = W₁ / M₁ – W₂ / M₂.

Таким представляется механизм возникновения колебаний угловой скорости около среднего значения. Амплитуда и частота колебания зависит как от свойств горной породы, так и от жесткости бурильной колонны. Так как вес бурильной колонны большой, то крутильные колебания вызывают значительные динамические нагрузки на долото в фазе замедления крутильных колебаний. Это может привести к преждевременному повреждению инструмента.

Неоднородность прочностных свойств горных пород приводит к тому, что перед лопастями долота разрушение происходит неодновременно. При этом наблюдается такая картина – вся буровая колонна и долото постоянно смещаются в сторону лопасти, перед которой порода не разрушилась. Это приводит к возникновению поперечных колебаний оси долота. Основная особенность развития поперечных колебаний заключается в том, что скважина приобретает форму многоугольника, число вершин которого на единицу больше числа лопастей долота.