II.1. Поскольку поршень вытаскивают из цилиндра медленно (без ускорения), то внешняя сила нарастает постепенно, оставаясь равной
F = (p0 − p)S +mg .
Поршень покинет цилиндр, если сила превысит значение
F = (
p0 −
p )
S +
mg ,
где 1 – давление воздуха в цилиндре в тот момент, когда поршень дос-тигает крайнего верхнего положения. В этом положении объем, зани-маемый воздухом, увеличился по отношению к первоначальному в два раза. Давление 1 определяется, исходя из закона Бойля–Мариотта:


æ
p0 +
mg ö
V =
p V .

Совместное решение записанных уравнений позволяет получить ответ:
F = 1 (
p0
S +
mg) .
Отметим, что найденное значение силы 1 является минимально доста-точным, для того чтобы медленно вытащить поршень из цилиндра.
129
Олимпиада «Ломоносов – 2007»

 II.2. Согласно первому закону термодинамики изменение внутрен-ней энергии газа
II.2. Согласно первому закону термодинамики изменение внутрен-ней энергии газа
∆U = Q − A.
Работа A , совершенная газом при переходе из состояния 1 в состояние 2, численно равна площа-ди трапеции 1234 (см. рис. 105):

Рис. 105
A = 1 (
p +
p2)(
V −
V ) .
Поскольку точки 1 и 2 лежат на прямой, проходящей через начало ко-ординат, справедливо равенство:


V =
p2 . 1 1
Поэтому в рассматриваемом процессе работа газа


A = 1 (
p +
p2) 1ç
p2 −1÷ . 1


Ответ: ∆
U =
Q −
A =
Q− 1 (
p +
p2)
V ç
p2 −1÷ =150 Дж. 1
II.3. Пусть
p0 , 0 и 0 – начальные, а
p ,
V и – конечные дав-ление, объем и температура газа. По первому закону термодинамики
Q = ∆U + A,

где ∆
U = 2
R(
T −
T ) – изменение внутренней энергии,
A – работа газа. Поскольку сжатие пружины совпадает с высотой поршня над дном сосуда, давление газа
p =
kx/
S пропорционально его объему:
p ~
V и


V =
V0 . При этом работа газа


A = 1 (
p +
p0)
V −
V ) = 1 (
pV −
p V ).
130
Решения задач
 Из уравнения состояния газа имеем:
Из уравнения состояния газа имеем:
p0 0 =
R 0 ,
pV =
np0
nV =
RT .


Отсюда
T =
n2
T . Следовательно,
A = 1
p V (
n2 −1) = 1
RT (
n2 −1),

∆
U = 3
RT (
n2 −1) . Ответ:
Q = 2
RT (
n2 −1) = 6225 Дж.
II.4. Поскольку плотность насыщенного водяного пара при комнат-ной температуре примерно на 5 порядков меньше плотности воды, а масса воды в начальном состоянии равна массе пара, объемом воды в цилиндре можно пренебречь. Обозначим давление насыщенного пара
через
p , а парциальное давление воздуха – через
x p . В соответствии с законом Дальтона начальное давление смеси равно
p0 = 1+
x)
pн . По-
сле изотермического уменьшения объема смеси в
k раз пар останется насыщенным (то есть его парциальное давление не изменится), парци-альное давление воздуха увеличится в
k раз, а давление смеси возрас-тет в
n раз:
np0 = 1+ kx)pн = n 1+ x)pн .


Отсюда
x =
n−
n =1, то есть начальное давление смеси равно
p0 =
k −1
pн = 2
pн . Так как масса воды в начальном состоянии равна
массе пара, то при изотермическом увеличении объема смеси в два раза вся вода испарится. При этом парциальное давление воздуха уменьшит-ся в 2 раза, и конечное давление под поршнем станет равным


pк =
рн + 1
х рн = 2
k −
n −1
рн =1,5
рн .


Следовательно,
р0 = 2(
k −1)1 = 0,75 , то есть давление смеси умень-шится в 4/3 раз.
131






Олимпиада «Ломоносов – 2007»
 II.5. Пусть перемещение l правого поршня таково, что пар в левом отсеке остается ненасыщенным. Обозначив через x смещение левого поршня, по закону Бойля-Мариотта имеем:
II.5. Пусть перемещение l правого поршня таково, что пар в левом отсеке остается ненасыщенным. Обозначив через x смещение левого поршня, по закону Бойля-Мариотта имеем:
pSL =
p S(
L−
l +
x) (для воздуха);
pSL =
p S(
L−
x) (для пара).
Отсюда
x =
l/2 , что справедливо, пока
p £ 2
p , т.е. при
l £
L . Когда
перемещение правого поршня превысит L , пар в левом отсеке начнет конденсироваться, и давление в обоих отсеках станет постоянным и равным 2p . Следовательно, постоянным и равным L/2 будет и рас-
стояние между поршнями. Длина левого отсека при этом
L¢= 2
L−(
l +(
L/2)) = 3
L/2−
l ,
и смещение левого поршня составит величину
x =
L−
L¢=
l −
L/2.
Если l ³ 3L/2 , пар полностью сконденсируется и левый поршень пере-станет перемещаться. Пренебрегая объемом образовавшейся в левом отсеке воды, получаем ответ в виде: x = l/ 2 при l £ L ; x = l − L/ 2 при
L £ l £ 3L/2 ; x = L при 3L/2 £ l £ 2L .
III. ЭЛЕКТРОДИНАМИКА
III.1. Пусть
m – масса каждого из шариков, 1 и
q2 – заряды ша-риков,
v – модуль скорости первого шарика в момент, когда расстояние между шариками равно 2
a , 1 и
v2 – модули скоростей первого и вто-рого шариков в момент, когда расстояние между ними равно 3
a . Из законов сохранения энергии и импульса следуют равенства:
q q2 q q2 m v2 4pe0a 4pe0 × a 2
q q2 q q2 m(v2 +v2 ) 4pe0a 4pe0 × a 2
m v =
m v −
m v2 .

Исключая из этих равенств
v и 4pe0
a , получаем уравнение
132
Решения задач

v2 −8
v v2 +
v2 = 0 ,



откуда
v =
v2 4± 15 . Условию задачи удовлетворяет больший по ве-личине корень. Ответ:
n =
v = 4+ 15 » 8 .
2
III.2. Ключевым моментом в условии этой задачи является тот факт, что сферы одинаковые. Отсюда следует, что при поочередном сопри-косновении шарика с каждой из сфер образуются тождественные друг другу системы проводников. Поэтому отношения заряда сферы к заряду шарика в обоих случаях должны быть одними и теми же. Если исходить из этого, то провести дальнейшие расчеты не составит труда. Пусть при соприкосновении шарика с первой сферой на него со сферы перетек заряд 1, а на сфере остался заряд
Q −
q . Тогда справедливо равенст-во:


1 − 1 2к 1
q2
Из закона сохранения электрического заряда, примененного к процессу соприкосновения шарика со второй сферой, следует, что
Q2 +
q =
Q2к +
q2 . Исключая из записанных уравнений
Q2к , получим
квадратное уравнение относительно неизвестной величины
q :
q2 +
Q2
q −
Q q2 = 0 .

Решая его, найдем, что
q = −
Q2 +
Q2 + 4
Q q2 . Следовательно,

Q2к =
Q2 +
q −
q2 =
Q2 − 2
q2 +
Q2 + 4
Q q2 = 3,5 мкКл.
III.3. При замкнутом ключе напряжение на конденсаторе 1 равно


2
U1 =
R + , конденсатор
C2 не заряжен, и энергия системы
W = 1 1 .
133
Олимпиада «Ломоносов – 2007»

Когда ключ разомкнули, конденсатор 1 разрядился через резистор, а конденсатор
C2 зарядился до напряжения
U2 =E . При этом энергия

системы стала равной
W2 =
C E 2 , а через источник протек заряд
q2 =
C E , в результате чего источник совершил работу
A =
q E . По закону сохранения энергии имеем:
W +
A =
W2 +
Q . Объединяя записанные выражения, получаем ответ:
2 2


Q = 2 è
C2 +
C (
R +
r)2 ø =1,32×10 Дж.
III.4. Поскольку конденсатор был полностью заряжен и отключён от источника, начальный заряд конденсатора равен q0 = CE . Здесь ис-пользовано определение электроёмкости конденсатора и тот факт, что конденсатор зарядится до разности потенциалов, равной ЭДС источни-ка. Начальная энергия – это энергия электрического поля заряженного конденсатора:

W =
CE2 .
В тот момент, когда заряд конденсатора уменьшится в n раз, эта энер-гия перераспределится между электрическим и магнитным полями, оставаясь неизменной:


W = (
q0 /
n)2 +
LI2 .
 Решая записанную систему уравнений, найдём силу тока в этот момент:
Решая записанную систему уравнений, найдём силу тока в этот момент:
I =
(n2 −1)C E
 L n
L n

C ×E = 50 мА.
134
Решения задач

 III.5. На рис. 106 изображена рамка АВСD, к вершинам А и D кото-рой подключен источник ЭДС. Таким образом,
III.5. На рис. 106 изображена рамка АВСD, к вершинам А и D кото-рой подключен источник ЭДС. Таким образом,
сторона рамки AD подключена параллельно уча-стку ABCD. В магнитном поле на проводники с током (стороны рамки) действуют силы Ампера. Направления магнитной индукции, токов и сил Ампера представлены на рис. 106. Пренебрегая внутренним сопротивлением источника и исполь-зуя закон Ома для полной цепи, найдем значения
токов
I1 и
I2 , текущих по участкам
AD и
ABC D: Рис. 106 4E E

 1 R 2 3R
1 R 2 3R
Из рис. 106 видно, что силы Ампера, действующие на стороны AB и CD, уравновешивают друг друга, а на стороны AD и BC – складываются. Поэтому на рамку действует результирующая сила, модуль которой равен
F =
F 1 +
F 2 = (
I1 +
I2)×
a×
B .
Здесь учтено, что плоскость рамки перпендикулярна направлению век-тора магнитной индукции B . Поэтому входящий в закон Ампера синус угла между проводником с током и вектором B для каждой из сторон рамки обращается в единицу. Подставляя в выражение для F найден-ные выше значения токов, находим ответ:

F = 16E
a B =1,6×10−2 H.
III.6. Рассмотрим момент времени, когда напряжение на катушке равно U . Обозначим через I L , I R , и I r силы токов, текущих в этот момент через катушку, резистор и источник, соответственно. По закону электромагнитной индукции

U =
L ∆
t ,
где ∆I L – изменение за малое время ∆t силы тока, текущего через ка-тушку. По закону Ома для однородного участка цепи напряжение на
135
Олимпиада «Ломоносов – 2007»
 резисторе
резисторе
U = I R R.
По закону Ома для участка цепи, содержащего ЭДС, U =E − I r r .
Поскольку согласно первому правилу Кирхгофа I r = I L + I R , из по-следнего равенства можно исключить переменную I r , переписав его в виде:

U =E −æ
I L +
U ö
r .
Кроме того, из записанных выше уравнений следует, что L∆I L = RI R∆t = R∆q ,
где ∆q = I R∆t – заряд, протекший через резистор R за время ∆t . Так как до замыкания ключа ток через катушку отсутствовал, а к рассматри-ваемому моменту времени стал равным I L , то LI L = Rq . Выражая от-сюда величину I L и подставляя ее в записанное выше соотношение для U , получим уравнение:


U =E −è
Rq +
U ø
r , из которого следует, что


R æ
Rrq ö
R+
r è
L ø

Заметим, что решение задачи существует при
q £ E
L , в противном
случае решения нет.
136
Решения задач
 IV. ОПТИКА
IV. ОПТИКА
 IV.1. Построение изображения для случая, когда правая линза сме-щена, приведено на рис. 107. Для
IV.1. Построение изображения для случая, когда правая линза сме-щена, приведено на рис. 107. Для
построения использованы два луча, идущие от источника: луч
1, совпадающий с главной опти-ческой осью левой линзы, и луч
2, проведенный в точку пересе-чения преломляющей плоскости левой линзы с главной оптиче-ской осью правой линзы. Из
рис. 107 видно, что на основании подобия треугольников h = Hx/ F . При вычислении величины учтем, что изображение источника, да-
ваемое левой линзой, находится на ее главной оптической оси на рас-стоянии 2F − L от правой линзы справа от нее. Используя для правой линзы формулу:





− 2
F −
L +
x =
F , находим, что
x =
F 2
F −
L . Ответ:
h =
H 2
F −
L .
 IV.2. Первое действительное изображение высотой h формируется лучами, которые исходят не-
IV.2. Первое действительное изображение высотой h формируется лучами, которые исходят не-
посредственно из стержня и преломляются линзой (см. рис. 108). Второе действи-тельное изображение высотой
h образуется при преломле-
нии линзой лучей, продолже-ния которых формируют мни-
мое изображение стержня в зеркале. Обозначим высоту стержня через H , расстояние между линзой и мнимым изображением стержня в зер-
137




Олимпиада «Ломоносов – 2007»

кале через
a , расстояния между действительными изображениями стержня и линзой через
b и
b . Из рисунка видно, что:
h b

 H a
H a
и h = b ,
1

причем
a =
a + 2(
x −
a) = 2
x −
a . Пусть
k =
h . В соответствии с фор-1
мулой тонкой линзы,





1 1 1 1 1
F a b a b
Отсюда находим, что
a a − F

 b F
b F
и a = a − F . Следовательно,
1



a b a −
F x −
F ab a −
F a −
F
Переписывая последнее уравнение в виде (k +1)(a − F) = 2(x − F) , по-лучаем ответ:

x = (
k +1)
a − (
k −1)
F .
Заметим, что, в силу условий a > F и k >1, величина x положительна.

IV.3 . Энергия одного кванта света
E =
hc . Пусть в единицу време-
ни на фотокатод падает n фотонов. Тогда мощность падающего света N = nE .
Только малая часть поглощенных фотонов вызывает фотоэффект. По ус-ловию задачи доля таких фотонов составляет всего h =1/k = 0,1=10% (это
– так называемый квантовый выход процесса). Поэтому количество элек-тронов, покидающих катод в единицу времени равно

n =
n .
138
Решения задач

Ток насыщения через фотоэлемент достигается при условии, что все покинувшие катод электроны достигают анода. Поскольку сила тока равна величине заряда, переносимого в единицу времени,
I =
n e.

Ответ:
I =
eNl =8 мА.

IV.4. Расстояние внутри пластинки свет проходит за время
t =
d , 1

где
v – скорость света внутри пластинки. Из волновой теории света известно, что 1 =
с , где
c – скорость света в вакууме. То же самое


расстояние в воздухе свет проходит за время
t2 =
d , где
v2 =
с . Та-2 0
ким образом, после внесения пластинки световая волна, прошедшая через пластинку, будет запаздывать по сравнению с волной, распро-страняющейся в воздухе, на промежуток времени

∆
t =
t −
t2 =
d n−
n ).

Такое запаздывание приводит к появлению сдвига фаз ∆f = w ×∆
t = w
d n−
n ),

где w = 2p – круговая частота, а
T – период колебаний в световой вол-

не. Учитывая, что l =
с T , получаем окончательно ∆f = 2p
d n−
n )= 3p .
139




 II.2. Согласно первому закону термодинамики изменение внутрен-ней энергии газа
II.2. Согласно первому закону термодинамики изменение внутрен-ней энергии газа











 Из уравнения состояния газа имеем:
Из уравнения состояния газа имеем:
















 II.5. Пусть перемещение l правого поршня таково, что пар в левом отсеке остается ненасыщенным. Обозначив через x смещение левого поршня, по закону Бойля-Мариотта имеем:
II.5. Пусть перемещение l правого поршня таково, что пар в левом отсеке остается ненасыщенным. Обозначив через x смещение левого поршня, по закону Бойля-Мариотта имеем:

















 Решая записанную систему уравнений, найдём силу тока в этот момент:
Решая записанную систему уравнений, найдём силу тока в этот момент: L n
L n

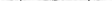 III.5. На рис. 106 изображена рамка АВСD, к вершинам А и D кото-рой подключен источник ЭДС. Таким образом,
III.5. На рис. 106 изображена рамка АВСD, к вершинам А и D кото-рой подключен источник ЭДС. Таким образом,
 1 R 2 3R
1 R 2 3R

 резисторе
резисторе





 IV. ОПТИКА
IV. ОПТИКА IV.1. Построение изображения для случая, когда правая линза сме-щена, приведено на рис. 107. Для
IV.1. Построение изображения для случая, когда правая линза сме-щена, приведено на рис. 107. Для




 IV.2. Первое действительное изображение высотой h формируется лучами, которые исходят не-
IV.2. Первое действительное изображение высотой h формируется лучами, которые исходят не-






 H a
H a






 b F
b F














