II.1. В закрытом цилиндрическом сосуде под невесомым поршнем находится идеальный газ (см. рис. 26). В пространстве над поршнем создан вакуум. Поршень удерживается в равнове-сии пружиной, помещенной между поршнем и крышкой ци-линдра, причем пружина не деформирована, если поршень располагается у дна цилиндра. Во сколько раз n возрастет объем газа, если увеличить его температуру в m = 2 раза?
Рис. 26 Толщиной поршня пренебречь.
II.2. В вертикальном цилиндрическом сосуде с площадью сечения S = 20 см2 под тяжелым поршнем находится идеальный газ. Когда со-
суду сообщают ускорение g /2 , направленное вверх, поршень устанав-
ливается относительно сосуда в таком положении, что объем газа под ним уменьшается в a =1,3раза. Считая температуру газа постоянной,
найти массу поршня M . Атмосферное давление p0 =105 Па, ускоре-ние свободного падения g =10 м/с2. Массой газа пренебречь.
30
Условия задач
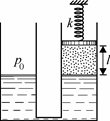II.3. В двух сообщающихся цилиндрических сосудах с одинаковой площадью поперечного сечения S находится во-
|
мирована и поверхность воды в обоих сосудах
находится на одном уровне. До какой температуры Рис. 27
T нужно нагреть воздух в сосуде, чтобы поршень переместился вверх на расстояние x ? Атмосферное давление p0 , плотность воды r , уско-
рение свободного падения g . Давлением водяных паров и трением при перемещении поршня пренебречь.
II.4. В космический корабль, совершающий межпланетный перелет, попал метеорит, пробивший в корпусе маленькое отверстие, через кото-рое наружу стал выходить воздух. Объем корабля V =1000 м3, началь-
ное давление воздуха в нем p0 =105 Па, температура t = 27 °C. Через какое время t после попадания метеорита давление воздуха в корабле
уменьшится на ∆p =103 Па, если площадь отверстия S =1 см2? Мо-лярная масса воздуха M = 29 г/моль, универсальная газовая постоянная R =8,3 Дж/(моль·К). При решении учесть, что ∆p << p0 , температуру
воздуха внутри корабля считать постоянной, а процесс истечения воз-духа квазиравновесным.
II.5. Два теплоизолированных сосуда объемом V = 40 л каждый со-
|
|
|
трубкой, объемом которой можно пренебречь. Какое давление p уста-
31
Факультет ВМиК
новится в сосудах после достижения теплового равновесия? Универ-сальная газовая постоянная R =8,3 Дж/(моль·К).
|
|
вратится в воду, если объем пара изотермически уменьшить до величи-ны V =1 л? Молярная масса воды M =18 г/моль.
II.7. Поплавок объемом V = 5 л целиком погружен в жидкость и
|
|
t0 = 0 °C равна r0 =103 кг/м3. Ускорение свободного падения принять равным g =10 м/с2.
III. ЭЛЕКТРОДИНАМИКА
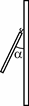III.1. Плоский лепесток толщиной d , сделанный из непроводящего материала плотностью r , подвешен за свою верхнюю точку
вплотную к тонкой вертикальной пластине, площадь которой значительно больше площади лепестка (см. рис. 28). На какой угол a отклонится лепесток от вертикали, если на него и на
|
Рис. 28 ускорение свободного падения g .
32
Условия задач
III.2. В плоский конденсатор вставлена диэлектрическая пластинка, как показано на рис. 29. На конденсатор подали напряжение U . Найти напряженность электрического поля E внутри диэлектрика, если расстояние между обкладками конденсатора d , толщина пластинки h , диэлектрическая
проницаемость диэлектрика e. Рис. 29
III.3. Две одинаковые металлические пластины площадью S каж-дая расположены параллельно друг другу на расстоянии d , весьма ма-
|
e0 .
III.4. Экран электронно-лучевой трубки представляет собой прямо-угольник с диагональю d =51 см и соотношением сторон 3:4. Сила то-
ка в электронном луче составляет I = 0,5 мА. Предположим, что все
электроны луча, попавшие на экран, остаются на нем, распределяясь по его поверхности равномерно. Через какое время t после включения
устройства напряженность электрического поля вблизи поверхности экрана достигнет по величине напряженности поля на поверхности уе-диненного металлического шара радиусом R =10 см, заряженного до
|
III.5. Пластины плоского воздушного конденсатора расположены горизонтально. Верхняя пластина сделана подвижной и удерживается в начальном состоянии на высоте h =1 мм над нижней пластиной, кото-
рая закреплена. Конденсатор зарядили до разности потенциалов U =1000 В, отключили от источника и освободили верхнюю пластину.
Какую скорость приобретет падающая пластина к моменту соприкосно-вения с нижней пластиной? Масса верхней пластины m = 4,4 г, пло-
щадь каждой из пластин S = 0,01 м2, электрическая постоянная
33
Факультет ВМиК
|
|
|
зарядов в конденсаторах, если перед подключением резистора заряды на конденсаторах были одинаковы?
III.7. Нагреватель с нихромовой спиралью развивает мощность N1 =500 Вт. При этом температура спирали нагревателя равна
|
t2 ? Напряжение, приложенное к нагревателю, неизменно. Температур-ный коэффициент сопротивления нихрома a =10−4 К–1. Тепловым расширением спирали пренебречь.
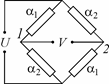III.8. Для измерения температуры t собрана схема, состоящая из четырех резисторов и подключенная к источнику с ЭДС U и малым внутренним сопротивлением (см. рис. 30). Температурные коэффициенты со-противления резисторов попарно равны и состав-ляют соответственно a1 и a 2 , а сопротивления
всех резисторов при температуре 0°С одинако-Рис. 30 вы. Как зависит напряжение V между точками 1
|
III.9. Электрический нагреватель для воды имеет две спирали. При подключении к сети одной из спиралей вода в нагревателе закипает че-
34
Условия задач
|
всех случаях одинаковы. Потерями тепла пренебречь.
III.10. Два параллельных металлических стержня расположены на расстоянии l друг от друга в плоскости,
перпендикулярной однородному магнит-ному полю с индукцией B (см. рис. 31).
Стержни соединены неподвижным про-
водником сопротивлением R . Два других Рис. 31
|
|
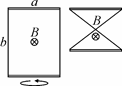III.11. Два прямых проводящих стержня соединены гибкими про-водниками и образуют прямоугольный контур
со сторонами a =30 см и b =50см (см. рис. 32).
Контур помещен в однородное магнитное поле с индукцией B = 5×10−3 Тл, направленной перпен-дикулярно его плоскости. Какой заряд ∆q про-
течет по контуру, если перевернуть на 180° Рис. 32
один из стержней, оставляя гибкие проводники натянутыми и не допус-кая замыкания между ними? Сопротивление контура R =1 Ом.
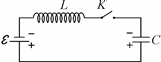*III.12. Цепь, изображенная на рис. 33, состоит из конденсатора, ка-тушки, источника с ЭДС E и пренебре-
жимо малым внутренним сопротивлени-ем, а также ключа К. В начальный момент времени ключ разомкнут, а конденсатор
заряжен до напряжения U0 с полярно-стью, указанной на рисунке. Какого мак-
Рис. 33
35
Факультет ВМиК
симального значения Umax может достичь напряжение на конденсаторе после замыкания ключа? Сопротивлением катушки и соединительных проводов пренебречь.
IV. ОПТИКА
IV.1. Оптическая схема, изображенная на рис. 34, состоит из непро-зрачного экрана с маленьким отверстием O и двух пло-ских зеркал 1 и 2. Луч света проходит через отверстие O, отражается от зеркал 1 и 2 и выходит обратно через это отверстие, причем угол падения луча на зеркало 1 равен
a , а после отражения от зеркала 2 луч распространяется
параллельно зеркалу 1. Когда зеркало 1 сместили влево параллельно самому себе на расстояние d1 , луч перестал попадать в отверстие O. На какое расстояние d2 нужно
Рис. 34
сместить параллельно самому себе зеркало 2, чтобы луч снова попал в это отверстие?
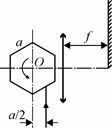IV.2. Оптический сканер представляет собой правильную шести-гранную призму с зеркальной поверхностью, вра-щающуюся вокруг свой оси О. Ширина каждой грани равна a . Снизу на сканер падает вертикаль-ный световой луч, продолжение которого прохо-дит на расстоянии a/2 от оси вращения сканера (см. рис. 35). Рядом со сканером вертикально рас-положена тонкая собирающая линза большого диаметра. Фокусное расстояние линзы равно f , а
|
линзы расположен широкий экран, нижний край которого расположен на оптической оси линзы. Определите длину d отрезка, который заме-тает на экране световой луч, отраженный от поверхности сканера.
36
Условия задач
IV.3. Луч света, распространяющийся в воздухе, падает в некоторой точке на поверхность стеклянного шара. После преломления и двух внутренних отражений от поверхности шара луч возвращается в точку падения и выходит из шара. При этом луч, падающий на шар, и луч, выходящий из него, оказываются перпендикулярными друг другу. Най-ти показатель преломления стекла n .
IV.4. К плоской поверхности тонкой плосковыпуклой линзы с фо-кусным расстоянием F =12 см прижато плоское зеркало. Со стороны
выпуклой поверхности линзы на расстоянии a =9 см от нее располо-
жен предмет. Построить изображение предмета и найти увеличение изображения m.
IV.5. Интерференционная картина "кольца Ньютона" наблюдается в отраженном монохроматическом свете с длиной волны = 0,63 мкм.
Интерференция возникает в заполненном бензолом тонком зазоре меж-ду выпуклой поверхностью плосковыпуклой линзы и плоской стеклян-ной пластинкой. Найдите радиус первого (внутреннего) темного кольца, если радиус кривизны поверхности линзы R =10 м, а показатели пре-
ломления линзы и пластинки одинаковы и превышают показатель пре-ломления бензола, равный n =1,5. Свет падает по нормали к пластинке.
37
Физический факультет
ФИЗИЧЕСКИЙ ФАКУЛЬТЕТ
В марте 2007 г. на физическом факультете проводилась устная олимпиада по физике «Абитуриент 2007». Задания, предлагавшиеся участникам этой олим-пиады, а также абитуриентам, сдававшим вступительные испытания в июле 2007 года, содержали две задачи и два теоретических вопроса, взятых из Про-граммы вступительных испытаний по физике, помещенной в настоящем сбор-нике. Результаты всех испытаний по физике на физическом факультете оцени-вались по 10-балльной шкале. При оценке ответов поступающих особое внима-ние уделялось обоснованию возможности использования при решении задач тех или иных законов, а также умению сформулировать предположения, при кото-рых полученное решение верно. Ниже приведены задачи, предлагавшиеся на олимпиаде и вступительном испытании по физике на физическом и физико-химическом факультетах в 2007 году. Кроме того, здесь же помещены задания по физике очного тура совместного проекта МГУ и газеты «Московский Ком-сомолец» «Покори Воробьевы горы». Перед номерами этих задач поставлен символ *.
I. МЕХАНИКА
|
между вторым и третьим – за t2 =1 с. Найти время t3 движения вело-сипедиста между третьим и четвертым столбами.
I.2. Автопоезд массой M =10 т двигался равномерно по прямой го-ризонтальной дороге. От него отцепился прицеп массой m = 4 т. Про-ехав после этого s = 300 м, водитель выключил двигатель и продолжил
движение накатом. Найти расстояние L между частями автопоезда по-сле их остановки. Считать, что силы сопротивления движению прицепа и тягача постоянны и пропорциональны их массам, причем коэффици-енты пропорциональности для прицепа и тягача одинаковы.
38
Условия задач
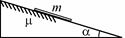I.3. Наклонная поверхность неподвижного клина с углом a при ос-новании имеет гладкую нижнюю и шерохова-
тую верхнюю части. Коэффициент трения меж-ду стержнем и верхней частью клина равен µ.
На верхней части клина удерживают тонкий Рис. 36
однородный стержень массой m, расположен-
ный в плоскости рис. 36. После того, как стержень отпускают, он начи-нает поступательно скользить по клину. Найти максимальную силу на-тяжения стержня в процессе его движения. Влиянием воздуха пренеб-речь.
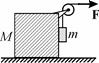*I.4. На гладкой горизонтальной плоскости располагается кубик с закрепленным на нем блоком. Масса кубика вместе с
блоком равна . Через блок перекинута гладкая невесомая нить, на которой висит груз массой m, касающийся вертикальной грани кубика. Коэффици-
ент трения груза о кубик равен . Первоначально
кубик и груз удерживают. Затем к свободному концу Рис. 37
нити прикладывают в горизонтальном направлении постоянную силу F , как показано на рис. 37, и одновременно отпускают кубик и груз. В результате они начинают двигаться поступательно, причем груз дви-жется вверх. Найти перемещение кубика ∆x к тому моменту, когда си-
ла F совершит работу A , а груз еще не коснется блока.
I.5. Математический маятник длиной L подвешен на гвозде, вби-том в вертикальную стену. Груз маятника отклонили так, что его нить приняла горизонтальное положение, параллельное стене, и была слегка натянута, а затем груз отпустили с нулевой начальной скоростью. На каком наибольшем расстоянии x под точкой подвеса следует вбить в стену второй гвоздь, чтобы после удара нити о него груз, двигаясь по окружности, поднялся на максимальную высоту?
I.6. На прямой круговой конус, ось которого вертикальна, надели тонкое гладкое кольцо радиусом R и массой m. Известно, что кольцо остается целым, если сила натяжения в нем не превышает F . Найти
39
Физический факультет
минимальное значение угла a между осью и образующей конуса, при котором кольцо не разорвется.
I.7. Две тонкие одинаковые доски верхними концами прикреплены к неподвижной горизонтальной оси О. Масса каждой доски равна m, а ее длина – L . Раздвинув доски, меж-
Рис. 38
ду ними поместили цилиндр массой M радиусом R так, чтобы точки касания цилиндра совпали с середи-ной досок (см. рис. 38). После того, как цилиндр от-пустили, он остался неподвижным. Найти коэффици-ент трения между цилиндром и доской. Трением в оси и деформациями тел пренебречь.
I.8. Период колебаний математического маятника на экваторе сфе-рической планеты в n =1,5 раза больше, чем на ее полюсе. Найти пери-од t обращения планеты вокруг ее собственной оси, если плотность вещества планеты = 3 г/см3.
I.9. На гладком горизонтальном столе лежат три одинаковых груза малых размеров массой m каждый, соединенные тремя легкими одина-ковыми пружинами жесткостью k . При этом грузы располагаются в вершинах правильного треугольника. Грузы смещают от положений равновесия так, чтобы удлинения всех пружин были одинаковыми. По-сле этого грузы одновременно отпускают. Определить период малых колебаний. Считать, что оси пружин остаются прямолинейными.
I.10. На гладком горизонтальном столе лежат одина-ковые грузы малых размеров, расположенные в верши-нах правильного n -угольника. Масса каждого груза рав-на m. Грузы соединены между собой одинаковыми лег-кими пружинами жесткостью k . Грузы смещают от по-ложений равновесия на одинаковые расстояния так, как показано на рис. 39. После этого грузы одновременно отпускают. Определить период малых колебаний. Счи-
Рис. 39 тать, что оси пружин остаются прямолинейными.
40
Условия задач
II. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА
II.1. В гладком вертикальном цилиндре под подвижным поршнем находится идеальный газ. При температуре t = 27 °C и давлении
p = 0,1 МПа объем газа V = 3 л. Для изобарического нагревания этого
|
|
II.2. В качестве рабочего вещества теплового двигателя используют гелий. На рис. 40 показана pV–диаграмма рабочего цикла этого двигате-ля. Найти КПД цикла.
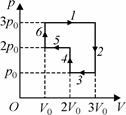
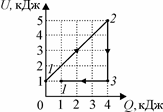Рис. 40 Рис. 41
II.3. На рис. 41 показана зависимость внутренней энергии U иде-ального газа, используемого в качестве рабочего вещества теплового двигателя, от количества теплоты Q , которое газ получил с момента 1 начала цикла 1−2−3−1. Найти КПД этого цикла.
II.4. В гладком вертикальном цилиндре под подвижным поршнем площадью S массой m длительное время находятся жидкость и ее пар при температуре Т. Атмосферное давление, действующее на поршень, равно p0 . Молярная масса жидкости равна µ, а ее удельная теплота парообразования в условиях опыта равна . На какую высоту ∆h под-
41
Физический факультет
нимется поршень, если жидкости передать количество теплоты Q , не-достаточное для ее полного испарения?
II.5. В сосуде содержатся идеальный газ и пар с относительной влажностью f при абсолютной температуре T под давлением p. Дав-
ление насыщенных паров при этой температуре равно pн . Молярная масса паров равна µп , а газа – µг . Определить отношение n плотности газа rг к плотности пара rп .
III. ЭЛЕКТРОДИНАМИКА
III.1. Четыре незаряженные одинаковые тонкие металлические пла-стины, площадь каждой из которых равна S , расположены в воздухе на малом расстоянии d параллельно друг другу (см. рис 42). Внутренним пластинам сообщили равные по модулю, но противоположные по знаку заряды. Затем внешние пласти-ны соединили между собой резистором сопротивлением R . В результате в этом резисторе выделилось количество теплоты
Q . Пренебрегая излучением, определить модуль q зарядов Рис. 42 внутренних пластин.
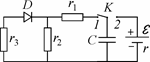*III.2. В изображенной на рис. 43 схеме ключ K длительное время находился в положении 1. Затем этот ключ перевели в положение 2, а потом через дос-таточно большой промежуток времени вновь вернули в положение 1. Найти отно-
шение работы сторонних сил батарейки к
|
III.3. Между двумя изолированными друг от друга параллельными металлическими пластинами со скоростью u протекает проводящая
42
Условия задач
жидкость. Расстояние между пластинами h намного меньше размеров пластин. Между пластинами создано однородное магнитное поле, век-тор индукции которого В параллелен плоскости пластин и перпендику-лярен u. К пластинам подключен конденсатор емкостью C . Найти максимально возможный заряд этого конденсатора.
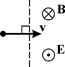III.4. Заряженная частица влетает со скоростью v в полупростран-ство, где существуют однородное электрическое поле с напряженностью E и однородное магнитное поле с ин-
дукцией B так, как показано на рис. 44. На какой угол отклонится частица от первоначального направления по-лета в момент ее вылета из этой области? Потерями энер-
гии частицы и действием на нее силы тяжести пренебречь. Рис. 44
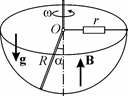III.5. Металлический стержень, один конец которого шарнирно за-креплен в точке О, вращают с такой постоянной
угловой скоростью w , что он образует с верти-калью постоянный угол a . Другой конец стержня касается проводящей полусферы (см. рис. 45). Центр полусферы совпадает с точкой О. Радиус полусферы равен R . Вся система находится в однородном вертикальном магнит-
ном поле, индукция которого равна В. К сфере Рис. 45 подключен резистор с достаточно большим сопротивлением . Другой конец резистора подключен к стержню в точке О. Найти мощность N ,
выделяющуюся в резисторе.
III.6. К идеальной катушке, зашунтированной резистором сопро-тивлением R , подключают на время t источник с ЭДС E и малым внутренним сопротивлением, а затем отключают его. При этом за время подключения источника и после его отключения в резисторе выделяют-ся одинаковые количества теплоты. Найти индуктивность катушки L .
43
Физический факультет
IV. ОПТИКА
IV.1. Тонкая собирающая линза помещена на границе раздела двух однородных сред с разными показателями преломления. Показатель преломления среды за линзой меньше, чем перед ней. Поэтому фокус-ные расстояния линзы не равны, причем f1 > f2 . Луч, падающий на линзу под небольшим углом к главной оптической оси, проходит через некоторую точку C на этой оси. Известно, что после прохождения лин-зы этот луч распространяется в том же направлении. Найти расстояние от точки C до линзы.
|
|
Рис. 46
оптической оси плоскостями, в которых располо-жены источник и его изображение.
|
|
Рис. 47
перпендикулярными главной оптической оси плоскостями, в которых расположены источник и его изображение, равно ∆a . Определить фокусное
расстояние F линзы.
44
Условия задач
ОЛИМПИАДА «ЛОМОНОСОВ – 2007»
В мае 2007 года в МГУ прошла олимпиада «Ломоносов – 2007». Подобные олимпиады проводятся в МГУ уже третий год подряд по согласованию с депар-таментами образования Москвы, Московской области, Советом ректоров вузов г.Москвы и Министерством образования и науки РФ. Диплом олимпиады «Ло-моносов-2007» приравнивается к диплому региональной олимпиады (3-й этап Всероссийской олимпиады). Олимпиада по физике традиционно проводится в форме устного испытания. В 2007 году участникам олимпиады предлагались задания, включающие два теоретических вопроса и три задачи различного уровня сложности. Ниже приведены задачи, предлагавшиеся участникам олим-пиады «Ломоносов – 2007».
I. МЕХАНИКА
|
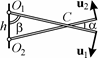
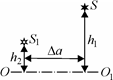
O2 . Расстояние между этими точками равно h . Най-
ти скорость движения точки С пересечения этих стержней вдоль первого стержня в тот момент, когда
|
, а скорости свободных концов стержней равны u1 и u2 .
I.2. На горизонтальной крышке стола лежат, касаясь друг друга, куб и цилиндр с одинаковыми массами (рис. 49). Коэф-
фициенты трения тел о поверхность стола и между собой одинаковы и равны µ. Диаметр цилиндра ра-
|
если к кубу приложить горизонтальную силу, линия действия которой перпендикулярна его грани и проходит через центры масс куба и ци-линдра, а модуль этой силы не меньше f , то цилиндр будет двигаться,
не вращаясь. Найти массу куба.
45
Олимпиада «Ломоносов – 2007»
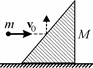I.3. О наклонную грань покоящегося на гладкой горизонтальной плоскости клина массой M =1 кг ударяется шарик
массой m = 20 г (см. рис. 50). Скорость шарика перед
|
шарик вернется в ту же точку пространства, где он столкнулся с кли-
ном. Удар считать абсолютно упругим, сопротивлением воздуха пре-небречь. Модуль ускорения свободного падения g =10 м/с2.
I.4. Развивая максимальную мощность двигателя, автобус движется
|
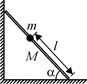I.5. Маленький шарик массой m закреплен на однородном стержне массой и длиной L на расстоянии l от его конца.
Стержень прислонен к вертикальной стене так, что образует с горизонтальной поверхностью угол a и располагается в вертикальной плоскости, перпендику-лярной стене (см. рис. 51). При каком максимальном
значении l стержень может находиться в равновесии? Рис. 51 Коэффициент трения стержня о горизонтальную по-
верхность и стену равен .
46
Условия задач
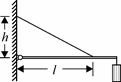I.6. К вертикальной стене одним концом с помощью шарнира при-креплен однородный тяжелый жесткий стер-
жень, на другом конце которого подвешен груз (см. рис. 52). Стержень удерживают в горизон-тальном положении легкой жесткой проволокой, прикрепленной к нему на расстоянии l = 30 см
от шарнира. Другой конец проволоки закреплен
на стене так, что проволока и стержень лежат в Рис. 52
одной вертикальной плоскости. На каком рас-
стоянии h от шарнира проволока должна быть прикреплена к стене, чтобы ее абсолютное удлинение было минимальным? Трением в шар-нире пренебречь.
I.7. На гладкий горизонтально закрепленный стержень надет шарик массой M . К шарику прикреплена легкая пружина, ось которой совпа-дает с осью стержня, а другой конец пружины закреплен. После откло-нения от положения равновесия шарик совершает гармонические коле-бания с амплитудой X0 . В момент прохождения шариком положения равновесия на него садится муха массой m, имевшая скорость, направ-ленную вертикально вниз. Найти амплитуду X1 установившихся гар-монических колебаний шарика с мухой.
I.8. К потолку покоящейся кабины лифта на пружине жесткостью k подвешена гиря массой m. В некоторый момент времени лифт начинает движение вверх с постоянным ускорением a . Какой путь S пройдет кабина лифта к тому моменту, когда длина пружины первый раз станет максимальной?
|
|
47
Олимпиада «Ломоносов – 2007»
ков, если их одновременно отпустить после небольшой деформации пружины. Силами трения пренебречь.
Дата: 2019-07-24, просмотров: 411.
