Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

II.1. В закрепленном вертикальном цилиндре площадью сечения S под гладким тонким поршнем массой m находится идеальный газ. Поршень находится в равновесии посередине цилиндра. В некоторый момент поршень начинают медленно вытаскивать из цилиндра. Какое значение примет прикладываемая к поршню сила в тот момент, когда поршень достигнет верхнего края цилиндра? Температура газа остается неизменной. Атмосферное давление p0 .

 

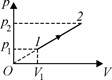II.2. На рис. 53 представлена зависимость дав-ления p от объема V идеального газа. Найти из-

 

1

менение внутренней энергии этого газа, если при изменении его давления от                                   p = 40 кПа до

 

 

 

Рис. 53

p2 = 60 кПа газу было сообщено количество теп-лоты Q = 200 Дж. В исходном состоянии объем

 

газа был равен V = 2 л.

 

 

1

0

II.3. В закрытом цилиндрическом сосуде под невесомым тонким поршнем находится один моль идеального одноатомного газа при температуре T = 300 К. В пространстве над порш-

 

нем создан вакуум. Поршень удерживается в равновесии легкой пружиной, помещенной между поршнем и крышкой цилиндра (см. рис. 54). Пружина не деформирована, если поршень располагается у дна цилиндра. Какое количество теплоты Q нужно сообщить газу, чтобы его объем увели-

Рис. 54   чился в n =1,5 раза? Универсальная газовая постоянная

 

R =8,3 Дж/(моль·К). Теплоемкостью сосуда, потерями теплоты и трени-ем пренебречь.

 

 

48

 

Условия задач

 

 

II.4. В цилиндре под поршнем находятся смесь воздуха с насыщен-ным водяным паром и вода. Масса воды равна массе водяного пара. Ес-ли изотермически уменьшить объем смеси в k = 2 раза, то ее давление увеличится в n =1,5 раза. Во сколько раз изменится давление смеси,

 

если ее объем не уменьшать, а увеличивать при той же температуре до тех пор, пока вся вода не испарится?

 

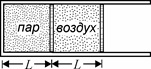II.5. В закрытом с одного конца цилиндрическом сосуде находятся два тонких поршня, способных переме-

щаться без трения и разделяющих про-странство внутри сосуда на два отсека (см. рис. 55). В левом отсеке заключен водяной пар при давлении p , а в правом – воздух

 

при том же давлении, причем длины отсе-                  Рис. 55 ков одинаковы и равны L . Правый пор-

шень медленно передвинули влево на расстояние l . На какое расстоя-ние x сместится при этом левый поршень? Температуру пара и воздуха считать постоянной. Давление насыщенного водяного пара при этой температуре равно 2p .

 

III. ЭЛЕКТРОДИНАМИКА

 

III.1. Два одинаковых маленьких шарика, заряженных одноимен-ными зарядами, удерживают на расстоянии a друг от друга. В некото-рый момент времени один из шариков отпускают без начальной скоро-сти, после чего он начинает движение. Когда расстояние между шари-ками становится равным 2a , отпускают без начальной скорости второй шарик. Определить, во сколько раз n скорость первого шарика будет превышать скорость второго шарика в момент, когда расстояние между ними станет равным 3a . Действием всех сил, кроме сил электростати-ческого отталкивания, пренебречь.

 

III.2. Две достаточно удаленные друг от друга и от других предме-тов одинаковые закрепленные металлические сферы имеют заряды

 

 

49

	C

 

 

Олимпиада «Ломоносов – 2007»

 

 

1

2

Q =8 мкКл и Q = 3 мкКл. Незаряженный металлический шарик на

 

тонкой длинной диэлектрической палочке подносят к первой сфере и касаются ее. Затем этот шарик переносят ко второй сфере и касаются ее таким же образом. Найти заряд Q2к оставшийся на второй сфере, если заряд шарика после его удаления от второй сферы оказался равным

q2 = 0,5 мкКл.

 

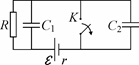III.3. В цепи, схема которой изображена на рис. 56, ключ К в тече-ние длительного времени находился в замк-нутом состоянии. В некоторый момент ключ разомкнули. Какое количество теплоты Q

 

 

 

Рис. 56

выделится в схеме после этого? Емкости кон-денсаторов: 1 =1 мкФ, C2 = 2 мкФ, сопро-тивление резистора R = 4 Ом, ЭДС источни-

 

ка E =10 В, его внутреннее сопротивление r =1 Ом.

 

 

III.4. Конденсатор ёмкостью C =1 мкФ полностью зарядили от ис-точника с ЭДС E =10 В и отключили от него. Затем конденсатор замк-нули на катушку, индуктивность которой равна L = 30 мГн. Найти силу

тока I в LC–контуре в тот момент, когда заряд конденсатора умень-шится в n = 2 раза по сравнению с максимальным. Потерями в LC– контуре пренебречь.

 

III.5. Из тонкого провода сопротивлением R =10 Ом изготовили квадратную рамку со стороной a =10 см. Рамку поместили в однород-

ное магнитное поле, вектор индукции которого перпендикулярен плос-кости рамки и по модулю равен B = 0,1 Тл. К вершинам двух соседних

 

углов рамки подключили источник с малым внутренним сопротивлени-ем и ЭДС E = 3 В. Найти силу, действующую на рамку со стороны

 

магнитного поля.

 

50

 

Условия задач

 

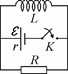III.6. В цепи, схема которой показана на рис. 57, в не-который момент замыкают ключ K. Найти напряжение U на катушке к тому моменту, когда через резистор проте-чет заряд q . Индуктивность катушки L , сопротивление

 

резистора R , ЭДС источника E , а его внутреннее сопро-

тивление .                                                                                             Рис. 57

 

IV. ОПТИКА

 

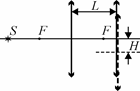IV.1. Оптическая система состоит из двух одинаковых тонких соби-рающих линз с фокусным расстоянием F

каждая. Линзы расположены на расстоянии L друг от друга ( F < L < 2F ) так, что их главные оптические оси совпадают (см.

Рис. 58

рис. 58). Слева от системы на расстоянии 2F от левой линзы находится точечный источник света S . На какое расстояние h сместится изображение источника, даваемое этой сис-

темой, если правую линзу сдвинуть перпендикулярно ее оптической оси на расстояние H ?

 

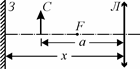IV.2. Оптическая система состоит из собирающей линзы Л с фокус-ным расстоянием               и плоского зеркала З,

плоскость которого перпендикулярна главной оптической оси линзы. Между линзой и зер-калом находится стержень C, расположенный перпендикулярно главной оптической оси

>

линзы. Расстояние от стержня до линзы равно                 Рис. 59 a , причем a                        F . Найти такое расстояние x

 

между линзой и зеркалом, при котором отношение размеров двух дей-ствительных изображений стержня равно k (k >1).

 

 

51

 

Олимпиада «Ломоносов – 2007»

 

 

IV.3 . На катод фотоэлемента падает свет с мощностью N = 0,3 Вт. Длина волны света                           = 330 нм. Найти силу тока насыщения I , если на каждые k =10 падающих на катод световых квантов приходится один фо-тоэлектрон. Считать, что постоянная Планка h = 6,6×10−34 Дж×с, скорость света в вакууме c = 3×108 м/с, модуль заряда электрона e =1,6×10−19 Кл.

 

IV.4. Два когерентных световых пучка проходят в воздухе одинако-вые расстояния от источников до некоторой точки A. На пути первого пучка перпендикулярно ему помещают прозрачную пленку толщиной

d = 2,5 мкм с показателем преломления n =1,3. На сколько в результа-

 

те этого изменится сдвиг фаз между световыми волнами в точке A, если длина волны света в вакууме l = 0,5 мкм? Показатель преломления воз-

 

духа n0 =1,0.

 

 

52

			l
	+
							2
					a

 

 

Решения задач

 

Р Е ШЕНИ Я З А Д А Ч

 

 

ФАКУЛЬТЕТ НАУК О МАТЕРИАЛАХ

 

 

t

1                1

2

1

1                                   2

1

1

2                    2

2            2

1. Пусть 1 – время, затраченное мотоциклистом на движение от на-чала колонны к ее концу, а t2 – время, затраченное на движение в об-ратном направлении. Пути, пройденные мотоциклистом при этих дви-жениях, соответственно равны s = l −v t и s2 = l +v t2 . Учитывая, что в обоих случаях мотоциклист начинает движение из состояния покоя, имеем: s = a t2 , s2 = a t2 , или a t2 = l −v t и a t2 = l +v t2 . Отсюда

 

 

1

a

t = − v +

v2   2

 

a2    a

и t2 = v +     v2 + 2 .

 

a

1                                            1

Полный путь, пройденный мотоциклистом, s = s + s2 = 2l +v(t2 −t ) .

 

æ

÷

ç

÷

a

Ответ: s = 2çl + v2 ö = 6 км. è           ø

 

 

∆S

2. Мысленно выделим на поверхности планеты небольшую площад-ку площадью ∆S . Так как основная часть атмосферы сосредоточена вблизи поверхности планеты (по условию атмосфера тонкая), то атмо-сферное давление равно p0 = ∆mg , где ∆m – масса столба атмосфер-

 

ного газа, находящегося над выделенной площадкой, g – ускорение

 

свободного падения на поверхности планеты. Следовательно, полная масса атмосферы m пропорциональна площади S поверхности плане-ты, то есть

 

g        g

m = Sp0 = 4pR2 p0 .

 

53

			=		2
	p						и

 

 

Факультет наук о материалах

 

 

2

3

Учитывая, что g = GM , где M = 4 pR3r – масса планеты, получаем

rG

R ответ: m = 3p0R .

 

3. Максимальное значение скорости груза, совершающего верти-кальные колебания на пружине, достигается при прохождении грузом положения равновесия, в котором сумма силы тяжести и силы упруго-сти растянутой пружины, действующих на груз, обращается в нуль. Примем положение равновесия груза за нулевой уровень отсчета потен-циальной энергии системы. При свободных незатухающих колебаниях полная механическая энергия системы сохраняется, откуда следует ра-венство:

 

0

+      =

.

k x2   m v2   m v2 2     2      2

Выражая из этого равенства жесткость пружины, находим ответ:

 

0

2

x

k = m v2 −v2 = 0,04 Н/м.

 

1

V

4. В соответствии с уравнением Менделеева–Клапейрона давление азота в начальном состоянии равно pн = mRT , где V – объем сосуда,

 

1

m – масса азота,   – его молярная масса. Давление газа в конечном состоянии определяется по закону Дальтона: pк = p + p2 , где

 

amRT 1       (M /2)V

 

=

2

p

(1−a)mRT 2  V

 

– парциальные давления атомарного и молекулярного азота, a – иско-мая доля диссоциировавших молекул. Следовательно,

 

2

=

p

.

mRT (1+a) к MV

 

54

 

Решения задач

 

 

По условию pк = npн . Объединяя записанные выражения, находим

 

1

T

a = nT −1. 2

 

2  1

Отметим, что относительная доля диссоциировавших молекул не может превышать единицу. Полагая в последнем равенстве a <1, получаем, что ответ имеет смысл при n < 2T /T . Следовательно, в общем виде

 

2

1

T

T

ответ формулируется так: a = nT −1 при n < 2T ; иначе решения нет. 2               1

 

 

5. Предложенное в условии задачи устройство предназначено для преобразования количества теплоты Q , полученного маслом при нагре-

 

Q

вании, в механическую работу A по перемещению рамы. В соответст-вии с определением коэффициента полезного действия, имеем h = A .

 

(

1

Fh

1

Количество теплоты, получаемое маслом, Q = t2 −t )C , совершаемая при этом работа A = F h . Ответ: h = C(t2 −t ) .

 

1      0                              0

6. На рис. 60 приведена эквивалентная схема рассматриваемой цепи, где сопротивления R = R l / L, R2 = R (L−l)/ L . Так

R

R

как резисторы 1 и 2 соединены параллельно, то

 

=  +

.

1  1  1

1       2

R R R                                                    Рис. 60

 

Отсюда находим, что искомое сопротивление R , которое покажет ом-

0

2

метр, равно R = l(L−l)R .

L

 

 

7. Сопротивление цепи, состоящей из последовательно соединен-ных резистора, катушки и конденсатора, и подключенной к источнику гармонического напряжения с циклической частотой                                                          , равно

 

55

 

Факультет наук о материалах

 

 

æ

ö

1

ç

÷

2 Z = R2 +èwL− wC ø ,

 

где R – сопротивление резистора. Мощность, потребляемая цепью от источника,

 

2

2

Z

N = 1 U0 cosf ,

 

где U0 – амплитуда напряжения источника, f – сдвиг по фазе между током в цепи и напряжением источника. Поскольку cosf = R , выраже-

 

ние для мощности, потребляемой цепью, можно переписать в виде

 

2

2

2

N = 1 U0 R .

Z

 

Так как при замыкании конденсатора потребляемая цепью мощность не изменяется, то величина Z остается неизменной:

 

ç             ÷

w

C

è             ø

R2 +æw L− 1 ö2 = R2 +(w L)2 .

 

 

Отсюда получаем ответ: w = 1 .

2LC

 

 

8. Пусть в момент времени  источник находится в точке S , а его изображение – в точке S1 (см. рис. 61). За

¢

¢

¢

время ∆t источник и изображение перемес-тятся и в момент t +∆t займут положения S¢ и S1 , соответственно, причем S S =V∆t , а

1                                                                                                    1

¢                          ¢

1

S1S =v∆t . Так как ∆ ASC подобен ∆ S BC , Рис. 61 а ∆ S SC подобен ∆ S1S C , справедливо ра-

 

¢

¢

S S   BC

венство S S = AC . В соответствии с формулой линзы 1 1

 

 

56

 

Решения задач

 

 

+    =

,

1    1   1 AC  BC  F

где BC = b . Отсюда следует, что

 

=

AC    F BC  b− F

 

v

F

Объединяя записанные выражения, получаем ответ: V = b− F .

 

ФАКУЛЬТЕТЫ ХИМИЧЕСКИЙ , БИОИНЖЕНЕРИИ И БИОИНФОРМАТИКИ

 

ВАРИАНТ 1

 

 

1. 3 . В инерциальной системе отсчёта частица движется по прямой, если сумма действующих на неё сил равна нулю. Следовательно, силы, действующие на протон со стороны электрического и магнитного поля, направлены в разные стороны и равны по величине. Из уравнения движения протона (второго закона Ньютона)

 

qE −q v B = 0

 

находим искомую скорость:

 

B

v = E = 2×105 м/с.

 

Рис. 62

1.4. Все необходимые построения выполнены на рис. 62. Прежде всего, для построения хода искомо-го луча надо найти положения фокусов линз – по условию они совпадают для рассеивающей и соби-рающей линз. Проведём побочную оптическую ось АВ, параллельную падающему лучу 1. Продолжение луча 2 пересекается с этой осью в передней фокаль-

ной плоскости линз. Отложив такое же расстояние за плоскостью линз,

 

57

.

 

 

Факультеты химический, биоинженерии и биоинформатики

 

 

находим заднюю фокальную плоскость. Луч 3 пересекается с побочной оптической осью в точке пересечения её с этой фокальной плоскостью.

 

 

1.5. Из уравнения состояния идеального газа p = nkT следует, что давление газа p пропорционально произведению его абсолютной тем-

пературы T и концентрации молекул n . Здесь k – постоянная Больц-мана. По условию температура газа увеличилась в 2 раза. Когда полови-на двухатомных молекул распалась на атомы, частиц в сосуде стало в 1,5 раза больше. Поскольку объем сосуда не изменился, концентрация частиц также возросла в 1,5 раза. Ответ: давление газа увеличилось в

a = 3 раза.

 

 

1.6. Поскольку по условию сопротивлением воздуха можно пренебречь, при решении проще всего воспользоваться законом сохранения механи-ческой энергии системы «сосулька + Земля». За нулевой уровень отсче-та потенциальной энергии тяготения удобно выбрать горизонталь, про-ходящую через точку соударения с поверхностью крыши BC. Точка от-рыва B находится выше этого уровня на h = lsina , поэтому равенство механических энергий в моменты времени, когда сосулька находится в точке B и в точке касания с участком крыши BC можно записать так:

 

0                                                 0

2                            2

m v2 +mglsina = mn2v2 .

 

 

 

Отсюда нетрудно получить ответ: v0 =

2glsina

 

n2 −1

 

 

1.7. Выберем инерциальную систему отсчёта, связанную с Землей, направив координатную ось Oy вертикально вверх к точке подвеса нити. На шарик действуют три силы – сила тяжести mg , сила натяжения нити

 

Л

T и сила Лоренца F (см. рис. 63). Запишем уравнение движения ша-

 

рика при прохождении им нижней точки траектории в проекции на ось Oy:

 

58

 

Решения задач

 

 

Л

maц.с. =T + F −mg .

 

F

Здесь учтено, что по правилу левой руки сила Лоренца Л , действующая на положительно заряженный ша-рик, направлена перпендикулярно скорости и вектору магнитной индукции поля B вдоль нити вверх. Цен-

тростремительное ускорение шарика равно:

 

v

2 ац.с. = l .

 

Скорость шарика в нижней точке траектории легко найти из закона сохранения механической энергии:

 

Рис. 63

 

2

mg l = m v2 .

 

Решая совместно записанную систему уравнений, получаем ответ: T =3mg −qB 2gl .

 

 

1.8. При нормальном падении на дифракционную решетку плоскопа-раллельного пучка монохроматического света от лазера дифракционные максимумы располагаются симметрично относительно центрального (ну-левого) максимума. Угловое положение максимумов определяется ус-ловием:

 

d sin  = ml ,

 

где m – порядок дифракции. Поскольку угол дифракции не может пре-вышать 90° (sinf £ 1), то максимальный порядок доступного для на-

 

ê ú

l

ë û

блюдения дифракционного максимума равен mmax = éd ù ,

 

где символ [L] означает целую часть числа. По условию наблюдаются

 

всего k = 7 максимумов. Это означает, что в данном случае mmax = 3. Следовательно, период решетки d > mmaxl . Однако, период решетки

 

 

59

 

Факультеты химический, биоинженерии и биоинформатики

 

 

должен быть меньше, чем (mmax +1)l , иначе будет наблюдаться меньше семи максимумов. Таким образом, период решетки лежит в диапазоне:

 

mmaxl < d < (mmax +1)l , т.е. 3l < d < 4l . Ответ: 1,9 мкм < d < 2,5 мкм.

 

 

1.9. Энергия электрического поля конденсатора равна

 

2

W =

.

CU1,2 1,2 2

 

Здесь U – разность потенциалов между обкладками конденсатора ем-костью C , а индексы 1 и 2 соответствуют исход-ному и замкнутому состоянию ключа K. Разность потенциалов U проще всего найти, если учесть, что она равна падению напряжения на параллель-ном с конденсатором однородном участке цепи, по которому протекает постоянный ток (исполь-

Рис. 64             зуя закон Ома для однородного участка цепи). При разомкнутом ключе (см. рис. 64) – это уча-

сток 1−3−2 , имеющий сопротивление 2R . По нижней ветви 1−4 −2 , включающей конденсатор, ток не течет. Поэтому сила тока, протекаю-щего по участку 1−3−2 , определяется законом Ома для полной цепи:

 

E

I1 = 2R+ ,

 

а интересующая нас разность потенциалов равна:

 

E

2

U1 = I1 × R = 2R + 2R.

 

После замыкания ключа полное сопротивление внешней цепи становит-ся равным 1,5R . Параллельно конденсатору теперь подключен участок 3−2 с сопротивлением R. Сила тока и разность потенциалов на этом

участке равны, соответственно:

 

E

E

I2 = 1,5R+r , U2 = I2R = 1,5R +r R .

 

 

60

 

Решения задач

 

 

Подставляя найденные значения разностей потенциалов в выражение для энергии конденсатора и беря отношение соответствующих величин, получаем ответ:

 

÷

ç

2

=

» 0,4

n =   =

.

ç          ÷

÷

ç

1

W  æU2 ö2   æ 2R + r ö2 W    èU1 ø     è3R + 2r ø

 

 

v

1.10. Решение задачи является хорошим примером применения за-конов сохранения в механике. Выясним, прежде всего, какие величины могут сохраняться для системы «шарик + клин». Поскольку удар абсо-лютно упругий, неизменной остается механическая энергия системы. Для решения задачи следует приравнять кинетическую энергию шарика не-посредственно перед соударением и кинетическую энергию клина и шарика сразу после соударения. Обозначив через v0 и 1 скорости ша-рика до и после удара, а через u – скорость клина после удара, имеем:

 

0            1

=      +

.

m v2    m v2   Mu2 2      2      2

Отметим теперь, что импульс системы «шарик + клин» при соударении, очевидно, изменяется: до удара он был горизонтален, а после удара по-является вертикальная составляющая этого импульса, связанная с от-скочившим вверх шариком. Физическая причина этого изменения также понятна – в процессе соударения появляется дополнительная состав-ляющая внешней силы – силы реакции опоры. Однако горизонтальная составляющая импульса системы сохраняется, поскольку реакция гладкой опоры не имеет проекции на это направление. Следовательно,

 

m v0 = Mu .

 

Самый тонкий момент в решении этой задачи – сообра-зить, что вектор изменения импульса шарика ∆p направ-

 

лен строго перпендикулярно наклонной поверхности кли-на. Эта поверхность также гладкая и импульс силы, дей-

ствующей на шарик со стороны клина в процессе удара,

не имеет касательной к этой поверхности составляю-     Рис. 65 щей. Остается сделать аккуратный рисунок (см. рис.65) с указанием векторов импульса шарика до и после удара, а также вектора изменения

 

61

	=		.

 

 

Факультеты химический, биоинженерии и биоинформатики

 

 

импульса шарика. Из рисунка видна связь модулей соответствующих импульсов:

 

1

m v = m v0 ctga .

 

Решая записанную систему уравнений, получаем ответ:

 

 

ctga =

M −m 7

 

M     8

 

ВАРИАНТ 2

 

 

2. 3 . Внутренняя энергия идеального газа прямо пропорциональна его абсолютной температуре. Поэтому, исходя из представленного в условии задачи графика, сначала следует построить зависимость температуры газа от его объема (см. рис. 66).

 

Рис. 66                                  Рис. 67

 

Теперь нетрудно установить, что процесс 1−2 изобарный, 2−3 – изохор-ный, а 3−4 – изотермический. Искомая диаграмма представлена на рис. 67. Здесь учтено, что точки 1, 2 и 4 лежат на одной изобаре (давления газа в этих точках одинаково), а также качественно соблюдены пропорции при изменении объема в процессах 1−2 и 3−4 . Участок 3–4 – отрезок ги-перболы.

 

 

2.4. Отметим прежде всего, что ультразвуковой вибратор – это кри-сталл, колеблющийся с ультразвуковой частотой, который может быть использован как генератор и как приёмник акустических волн. Обозна-чим через v скорость воздушного потока относительно лабораторной системы отсчёта, а через U скорость звука относительно воздушного потока, причём U > v . Используя закон сложения скоростей, запишем

 

62

 

Решения задач

 

 

(

равенства:

1

L = U +v)t – для распространения звука вдоль потока, и

 

(

2

L = U −v)t – для распространения звука против потока.

 

(  )

2    1

t t

2

Здесь L – расстояние между вибраторами. Решая эту систему уравнений, получаем ответ: v = L t −t =17,4 м/с.

 

1 2

 

 

2. 5 . Обозначим через угол преломления. По закону преломления

 

= n,

sina sinb

 

где n – показатель преломления вещества относительно воздуха. Абсо-лютный показатель преломления воздуха мало отличается от единицы. Поэтому n можно считать равным абсолютному показателю преломле-ния вещества. Учитывая, что по условию угол между отраженным и преломленным лучами прямой, и используя закон отражения, можно записать соотношение a +b = p/2. Отсюда следует, что sinb = cosa .

 

Тогда из закона преломления вытекает равенство: tga = n . Согласно волновой теории света

 

v

n = c ,

 

где c – скорость света в вакууме, v – скорость света в веществе. Ответ:

 

c

×

v = tga »1,73 108 м/с.

 

 

2.6. Эта задача является хорошей иллюстрацией применения закона Ома для неоднородного (содержащего ЭДС) участка цепи. Чтобы найти заряд q на пластинах конденсатора в предложенной схеме, необходимо

 

вначале определить разность потенциалов | 1 −f2 |=U между обклад-ками конденсатора. По определению электроёмкости конденсатора C она связана с абсолютной величиной заряда его обкладок равенством:

 

63

 

Факультеты химический, биоинженерии и биоинформатики

 

 

U

C = q .

 

Поскольку конденсатор подключен к полюсам источника параллельно, искомую разность потенциалов можно найти, записав закон Ома для неоднородного участка цепи. Учитывая, что ток через источник проте-кает от положительного полюса к отрицательному (работа сторонних сил отрицательна), а сопротивление участка равно сопротивлению ис-точника r , имеем:

 

=

.

I

f1 −f2 −E r

 

Отсюда f1 −f2 =E + Ir . Ответ: q = C(E + Ir) =1,2×10−5 Кл.

 

Зам е ч а н и е . Полезно построить график изменения потенциала

 

Рис. 68

вдоль рассматриваемого участка цепи 1−2 (см. рис. 68). В случае обычного (химического) источ-ника потенциал падает скачками при переходах «положительный полюс источника – электролит» и «электролит – отрицательный полюс источника», и равномерно уменьшается при протекании тока че-рез электролит, т.е. на внутреннем сопротивлении источника. Из графика нетрудно видеть, что вели-чина искомой разности потенциалов действительно

равна f1 −f2 =E + Ir . Приведенный анализ поведения потенциала на участке цепи, содержащем источник, помогает дать ответ ещё на один важный вопрос: что покажет вольтметр, подключенный к клеммам источника? Идеальный вольтметр в рассматриваемом случае (когда ток через источник течет от положительной клеммы к отрицательной) покажет напряжение U1 =E + Ir . В частности, такой случай реализует-ся, при зарядке аккумуляторов. Если ток через источник течет от отри-цательной клеммы к положительной, то вольтметр покажет напряже-ние U2 =E − Ir . Предлагаем обосновать этот результат самостоятельно, построив график зависимости потенциала вдоль участка цепи также и для этого случая.

 

64

 

Решения задач

 

 

2.7. Скольжение бруска вдоль наклонной поверхности клина проис-ходит под действием двух сил: силы тяжести mg и

 

силы реакции наклонной плоскости N , которая в

 

отсутствии трения перпендикулярна плоскости (см. рис. 69). По второму закону Ньютона для бру-ска в проекциях на направления вдоль наклонной плоскости и перпендикулярное к ней имеем:

 

Рис. 69

 

ma = mgsina ,   0 = N −mgcosa .

 

¢

F

По третьему закону Ньютона брусок действует на наклонную плоскость с силой N = −N . Поскольку клин неподвижен, то векторная сумма всех сил, действующих на него, равна нулю. Равна нулю и сумма проекций сил на горизонтальное направление. В горизонтальном направлении на клин действуют силы: вправо – сила реакции стенки n , влево – горизонтальная составляющая силы давления бруска, равная по модулю Nsina . По вто-рому закону Ньютона для клина имеем:

 

n

0 = F − Nsina . Решая записанную систему уравнений, получаем:

 

×

n

ö

æ

a   a

÷

ç

g

ø

è

F = mgcosa sina = mg 1−ç g ÷2 ×g = m a  g2 −a2 .

 

F

g

Наконец учтём, что по третьему закону Ньютона искомая сила нор-мального давления клина на стенку равна по модулю силе реакции стен-ки n . Ответ: P = m a                                         g2 −a2 = 0,48 Н.

 

2.8. Исходя из указанной в условии задачи зависимости между темпе-ратурой и объемом газа, делаем заключение, что температура газа квадра-тично зависит от его объема:

 

T ~V 2 .

 

В соответствии с объединённым газовым законом параметры заданного количества идеального газа в любом процессе связаны друг с другом соот-ношением:

 

 

65

 

Факультеты химический, биоинженерии и биоинформатики

 

 

pV = const .

 

Из этих выражений следует, что в рассматриваемом процессе давление газа растет пропорционально объему ( p ~V ). Для опреде-

 

ления работы газа удобно представить процесс его рас-ширения на pV–диаграмме (см. рис. 70). Работа числен-но равна «площади под графиком» зависимости p от

 

p

V

V . В нашем случае это – площадь трапеции с основа-Рис. 70                     ниями 1 , p2 и высотой V2 − 1 . Имеем:

 

1

(

1                 2            1 1     1            2 1

2

2

A = p + p2 ×V2 −V ) = 1 (p V2 − p V + p V2 − p V ) .

 

Поскольку точки 1 и 2 лежат на прямой, проходящей через начало коорди-

 

p  V

2        2

нат, справедливо равенство p1 = V1 . Следовательно, выражение для рабо-ты газа принимает вид:

 

2            1 1

2

A = 1 (p V2 − p V ) .

 

Согласно уравнению состояния идеального газа, pV = nRT ,

 

где n – число молей газа. Поэтому искомая работа равна

 

2    1

2

A = 1 R(T −T ) =1245 Дж.

 

2.9. Линейное увеличение k изображения предмета, даваемого линзой – это отношение линейного размера изображения к линейному размеру предмета. Как легко убедиться, оно равно отношению расстояния f от

 

d

линзы до изображения к расстоянию d от предмета до линзы: k = f .

 

 

66

 

Решения задач

 

 

1

Когда предмет находится на двойном фокусном расстоянии от соби-рающей линзы (d = 2F ), его изображение формируется на таком же расстоянии за линзой, т.е. f1 = 2F (это можно проверить с помощью фор-мулы линзы или путем построения). Размер этого изображения совпадает с размером предмета, поэтому k =1.

 

Расстояние между изображением предмета и рассеивающей линзой можно найти с помощью формулы линзы:

 

2

f     F      F

− 1 + 1 = − 1 . 2

 

3

Знак «минус» в левой части формулы, отражает тот факт, что изображе-ние предмета мнимое, а знак «минус» в правой части – тому, что линза рассеивающая. Из этой формулы следует, что f2 = 2 F . Поэтому ли-

 

2F   3

нейное увеличение во втором случае k2 = 2F /3 = 1 . Ответ:

 

k

k1 = 3. 2

 

 

2 .1 0 . Прежде всего, отметим, что момент максимального растяжения пружины соответствует нижнему положению груза в процессе его вер-тикальных колебаний. В этот момент пружина растянута на величину

 

∆x = x0 + A ,

 

где A – амплитуда колебаний грузика. Здесь учтено важное обстоя-тельство, что в положении равновесия системы пружина уже растянута. Величина этого растяжения x0 соответствует равенству сил тяжести и упругости:

 

0 = mg −kx0 .

 

2

Потенциальная энергия пружины в интересующий нас момент равна Eп = k∆x2 .

 

 

67

 

Факультеты химический, биоинженерии и биоинформатики

 

 

Чтобы найти эту величину, необходимо, таким образом, найти параметры A и k . Амплитуда колебаний A , очевидно равна половине расстояния S между двумя крайними положениями грузика:

 

2

A = S .

 

Жёсткость пружины связана с периодом колебаний грузика T хорошо известным соотношением:

 

k

T = 2p m .

 

В свою очередь период колебаний равен удвоенному времени движения грузика между двумя крайними положениями:

 

T = 2t.

 

Решая записанную систему уравнений, получаем ответ:

 

t + p

(2             )

m g        S

2      2  2

Eп =      8p2t2            » 0,2 Дж.

 

ВАРИАНТ 3

 

 

3.3. По закону Фарадея ЭДС индукции Ei равна скорости измене-ния магнитного потока F через поверхность, ограниченную проводящим контуром:

 

F

d

Ei = − dt .

 

i

2 c

Следовательно, Ei  определяется наклоном гра-фика зависимости F (t) . В промежутке времени от 0 до 2 с величина ЭДС постоянна и равна E 1 = − 2 Вб = −1 В. Такая же ЭДС индуцирует-

 

Рис. 71               ся в промежутке от 12 с до 16 с. В промежутке

 

68

 

Решения задач

 

 

2 c

времени от 6 с до 8 с ЭДС Ei2 = 4 Вб = 2 В. На горизонтальных участ-

 

ках графика ЭДС равна нулю, т.к. изменения магнитного потока не про-исходит. Соответствующая зависимость представлена графически на рис. 71.

 

 

3.4. При движении брусков из начального положения в конечное потенциальная энергия каждого из них изменяется на одну и ту же ве-личину. В соответствии с законом сохранения энергии часть потенци-альной энергии каждого из брусков перейдет в кинетическую энергию, а часть израсходуется на работу против силы трения. Брусок, который был пущен вниз, пройдет до основания наклонной плоскости меньший путь, чем другой брусок. Следовательно, для этого бруска работа про-тив силы трения будет меньше, чем для бруска, пущенного вверх. От-вет: у основания наклонной плоскости бóльшую скорость будет иметь брусок, который пущен вниз.

 

 

3.5. В исходном положении поршня силы, действующие на него со стороны воздуха, находящегося внутри и снаружи цилиндра, уравнове-шены. Каждая из этих сил по модулю равна

 

1

4

F = p0S = p0 pd2 .

 

При вытаскивании поршня из цилиндра давление воздуха в цилиндре уменьшается, и к поршню приходится прикладывать все увеличиваю-щуюся силу. Когда поршень находится у открытого конца цилиндра, эта сила максимальна. В этом положении поршня объем воздуха в цилинд-ре увеличится в два раза, а его давление по закону Бойля-Мариотта уменьшится в два раза. В два раза уменьшится также сила давления на поршень со стороны воздуха в цилиндре, а сила атмосферного давления останется прежней. Поэтому к поршню должна быть приложена сила, направленная наружу и не меньшая, чем

 

p

2

F = p0S = p0 8d2 = 20 Н.

 

 

69

 

Факультеты химический, биоинженерии и биоинформатики

 

3.6. При разомкнутом ключе батарею можно представить в виде двух параллельно соединенных участков, в каждом из которых после-довательно соединены конденсаторы с электроемкостями C и 3C . В

 

1

2

этом случае эквивалентная ёмкость батареи C = 3 C .

 

При замкнутом ключе батарею можно представить в виде двух последо-вательно соединенных участков, в каждом из которых конденсаторы C и 3C соединены параллельно. В этом случае ёмкость батареи C2 = 2C . Ответ:           при               замыкании                 ключа  ёмкость   увеличилась  в

С

3

k = С2 = 4 =1,33 раза. 1

 

 

3.7. Количество теплоты, выделяемое нагревателем за промежуток времени t,

 

R

Q = U 2 t.

 

За вычетом тепловых потерь на плавление льда пойдет количество теп-лоты

 

U

2

1

Q = Q(1−k) = R (1−k)t.

 

С другой стороны, для того чтобы расплавить массу льда m требуется количество теплоты

 

2

Q = lm .

 

(

1      2

l m

Приравнивая Q = Q , получаем ответ: R = U 2t 1−k)» 5,3 Ом.

 

70

 

Решения задач

 

 

3.8. При решении задачи главное – это установить, по какой траек-тории движется центр стержня (точка С). Для

этого следует сделать аккуратный чертеж (см. рис. 72) и убедиться из равенства прямоугольных треугольников (например, ∆ Ox c C и ∆ Cx c B ), что расстояние ОС – постоянная величина, равная половине длины стержня. Следовательно, траек-

2

тория, по которой движется центр стержня, пред-            Рис. 72 ставляет собой дугу окружности радиусом R = l

 

с центром в точке O. Путь, проходимый точкой C в рассматриваемом движении стержня, равен четверти длины этой окружности. Ответ:

 

4    4

S = 2p R = pl » 0,8 м.

 

R

3.9. Если бы в той части цепи, где включен резистор 1 , не было

 

диода, то количество теплоты, выделившейся на этом резисторе за вре-мя t, было бы равно

 

t

U

U

д

2                 2

0

1

1                           1

Q¢= R ∆t = 2 R .

 

При включенном в цепь диоде ток через резистор отличен от нуля толь-ко в течение половины каждого периода. Поэтому на резисторе выделя-ется вдвое меньшее количество теплоты:

 

t

U

1

2

0

1            1

1

Q = 2 Q¢= 4 R .

 

Аналогично, количество теплоты, выделившееся на резисторе R2 , рав-но

 

t

U

0

2

Q2 = 4 R2 .

 

Общее количество теплоты, выделившееся на обоих резисторах,

 

 

71

 

Факультеты химический, биоинженерии и биоинформатики

 

 

2

U

0

1

1

R R

1  2

Q = Q +Q2 = 4 (R + R2 )t= 90 Дж. Заметим, что полярность включения диодов не играет роли.

 

B

3.10. Построение изображения A¢ ¢ стержня AB приведено на рис. 73. Для построения использованы два лу-ча. Луч 1 проходит без преломления через оп-тический центр линзы. Луч 2 направлен вдоль стержня и после преломления в линзе пересе-кает ее правую фокальную плоскость в точке D. Отметим, что луч 2 выбран не случайно. Подобные лучи испускают все точки стержня,

Рис. 73                поэтому изображение стержня располагается на прямой, имеющей такой же наклон к главной оптической оси линзы, что и луч 2 после преломления в линзе. Из рисунка видно, что

 

¢

O A

tgb = O C .

 

Кроме того, из подобия ∆ O CA¢и ∆ CE D следует, что

 

¢

EC

O A = E D×O C .

 

Поскольку по условию Ð AOC = 45°, справедливы равенства: OC = d , E D = F , EC = d − F . Решая записанную систему уравнений, находим

 

F

F

tgb = d − F . Ответ: b = arctg d − F = arctg2 » 63,4°.

 

ВАРИАНТ 4

 

 

4.3. Приведенная на рис. 14 зависимость координаты материальной точки от времени описывается выражением

 

x = xmax cos t ,

 

 

72

 

Решения задач

 

 

T

где xmax – амплитуда, w = 2p – круговая частота, T – период колеба-

 

ний. Проекция скорости точки на ось Ox равна производной от коорди-наты по времени:

 

d t

v = d x = −xmaxw sinw t .

 

T

Отсюда находим максимальную величину скорости: vmax = xmaxw = xmax 2p .

 

Значения xmax = 2 см и T = 8 с определяются из графика. Ответ: vmax »1,57 см/с.

 

 

4.4. Задача решается очень просто, если знать особенности использо-вания собирающей линзы в качестве лупы. Для того чтобы получить уве-личенное мнимое изображение предмета, его располагают вблизи фокаль-ной плоскости линзы между линзой и фокусом. Записывая формулу линзы, имеем:

 

=       −

.

1    1    1 F  F − x  f

 

Это равенство легко преобразуется в квадратное уравнение относительно фокусного расстояния линзы

 

F2 − xF − xf = 0 , корни которого имеют вид:

1

2

4

F,2 = 1 x±     1 x2 + xf .

 

Для собирающей линзы следует выбрать положительный корень. Фокусное расстояние линзы равно F = 5 см, а её оптическая сила D = 1 = 20 дптр.

 

 

73

	=		=		.

 

 

Факультеты химический, биоинженерии и биоинформатики

 

 

4.5. Обозначим через a угол, который образует крыша с горизонта-лью. В отсутствии трения тела скользят вдоль крыши (наклонной плос-

 

L

кости) с ускорением a = gsina . Длина наклонной плоскости S = cosa . Из законов кинематики прямолинейного равноускоренного движения следует, что расстояние S скользящее тело проходит за время

 

 

t =

2S             2L                 4L

 

a     g cosa sina      gsin2a

 

Время скольжения минимально при максимальном значении sin2a , которое достигается при a = 45° . Ответ: H = L = 2,5 м.

 

 

1

4.6. При равновесии поршня равнодействующая всех сил, дейст-вующих на него, равна нулю. Снизу вверх на поршень действует сила давления воздуха, находящегося в цилиндре, F = pS , где p – давление

 

4

воздуха, S = pd2  – площадь поршня. Сверху на поршень действует

 

2

3

сила атмосферного давления F = p0S , где p0 – атмосферное давление. Вниз также направлена сила тяжести F = Mg , действующая на пор-

 

F

4

шень, и сила давления стержня 4 . Последняя вычисляется по правилу моментов и равна F = 2mg . Учитывая направления сил, условие рав-новесия поршня запишется в виде:

 

p0S + Mg + 2mg = pS .

 

Отсюда находим искомую величину

2

p

d

∆p = p− p0 = 4(M +2m)g » 4×103 Н.

 

4.7. Рассмотрим электрическую схему, описанную в условии (см. рис. 74). В процессе разрядки конденсатора после замыкания ключа K через резисторы протекает ток, сила которого меняется во времени, по-степенно убывая. Однако в любой момент времени через резисторы те-

 

 

74

 

Решения задач

 

 

чет одинаковый ток. Согласно закону Джоуля–Ленца мощности, выде-ляющиеся                   в резисторах, равны, соответственно

R

N1 = I2 1 , N2 = I2R2 . Их отношение

 

R

=

N1         1

 

N2    R2

не зависит от времени. Поэтому такое же отношение         Рис. 74 справедливо и для количеств теплоты, выделившихся в конденсаторах за время разрядки конденсатора:

 

1        1

=

.

Q   R Q2   R2

При этом полное количество выделившейся теплоты равно энергии, запасенной в конденсаторе:

 

1      2

2

Q +Q = C U2 .

 

Из этих соотношений находим ответ:

 

R

U

1

1

1

Q = C2 2 R + R2 = 5×10−4 Дж.

 

 

0

S

4.8. Обозначим через V0 начальный объём газа. Очевидно, что в ис-ходном состоянии пружина не деформирована. Пусть в нагретом со-стоянии газ занимает объем V . При этом пружина удлинилась на вели-чину x = V −V . Теперь со стороны пружины на поршень действует

 

сила упругости, величина которой равна

 

0

S

F = k x = k V −V .

 

Главное – понимать, что в любом равновесном состоянии векторная сумма всех сил, действующих на поршень, равна нулю, т.е.

 

F + p0S = pS .

 

 

75

 

Факультеты химический, биоинженерии и биоинформатики

 

 

Здесь p – давление газа в объеме V . Из последнего соотношения нахо-дим ответ:

 

(

2

S

p = p0 + k V −V0 ).

 

Отсюда видно, что давление газа увеличивается при расширении по линейному закону (см. рис. 75), причем при объеме V0  давление равно

 

p0 . Наклон прямой зависит от отношения величин Рис. 75                         k и S2 .

 

 

4.9. Условие плавания льда массой m имеет вид: mg = V g .

 

Здесь V – объем погруженной в воду части льда, равный объему вы-тесненной льдом воды, r – плотность воды. Высота подъема уровня

 

4

воды h определяется из условия V = Sh , где S = pd2  – площадь осно-

 

вания цилиндрического сосуда. Из этих соотношений получаем ответ:

 

4m

h = rpd2 » 4,8 см.

 

Заметим, что этот ответ справедлив для любого тела массой m, не обя-зательно льда. Важно лишь, чтобы погруженное в воду тело оставалось на плаву.

 

 

4.10. Так как при замыкании ключа ток по нему не течет, разность потенциалов между точками, которые соединяются ключом K, равна нулю. Отсюда вытекает, что

 

1        3

R  R

3

R

R = R и R4 = R2R = 4 Ом. 2      4                                1

 

Следовательно, ключ K из схемы можно удалить. После этого легко найти полное сопротивление цепи, подключенной к источнику тока,

 

 

76

 

Решения задач

 

 

пользуясь правилами последовательного и параллельного соединений резисторов:

 

R         R

= 4

=

Ом.

R

R             R

( 1 + R2)( 3 + R4 ) ( 1 + R2 )+( 3 + R4 )

 

R

Сила тока через источник определяется по закону Ома. Ответ: I = E =1,5 А.

 

БИОЛОГИЧЕСКИЙ ФАКУЛЬТЕТ

 

 

3. Работа, совершаемая против электрического поля при перемеще-нии в нём заряда q , определяется формулой

 

A = q×∆ ,

 

где ∆f – разность потенциалов между точками, соответствующими конечному и начальному положениям заряда. Для однородного поля

∆ = E L,

 

где E – модуль напряженности электрического поля, L – перемещение заряда вдоль силовой линии поля. Решая записанные уравнения, полу-

 

А

чаем ответ: E = q L = 2,5×103 В/м.

 

 

4. Искомая зависимость давления газа от его объема (pV-диаграмма процесса) представлена на рис. 76. Отметим, что

Рис. 76

участки 1 – 2 и 4 – 5 являются гиперболами, описы-вающимиизотермические зависимости, 2 – 3 и 3 – 4 – прямыми, параллельными осям координат и соответствующие изобарному и изохорному про-цессам. Следует обратить внимание на то, что точки 1, 3 и 4 находятся на одной вертикальной

прямой (объём, занимаемый идеальным газом в этих состояниях одина-

 

 

77

 

Биологический факультет

 

 

ков). В состояниях 2 и 5 давление газа одно и то же (штриховая линия 1 – 5 параллельна оси абсцисс).

 

 

1

5. Если длительность соударения является пренебрежимо малой, то сумма проекций всех сил, действующих на систему «шарик + брусок», вдоль направления движения тел равна нулю. Поэтому импульс систе-мы сохраняется: m v = m2u . Отсюда легко определить начальную ско-рость шарика:

 

m

v = m2u . 1

 

По закону сохранения энергии начальная кинетическая энергия шарика равна сумме кинетической энергии бруска (шарик по условию задачи остановился и, следовательно, не обладает кинетической энергией) и количества теплоты Q, выделившейся при ударе:

 

v

1              2

2

m2 2 = m u2 +Q .

 

Таким образом, искомое количество теплоты Q может быть определено как разность кинетических энергий системы до и после удара. Ответ:

 

1

2m

Q = m2(m2 −m )u2 = 3×10−2 Дж. 1

 

 

6. Используя кинематический закон равноускоренного движения, перемещения мотоциклиста S на двух равных отрезках пути можно записать в виде:

 

1 1

2

2

1

2

S = a t2   и S = ∆v ×t2 + a2t2 ,

 

v

t

где 1 и t2 – времена прохождения мотоциклистом этих отрезков, а ∆ 1 – скорость, которую имел мотоциклист перед прохождением второго отрезка. Здесь мы учли, что мотоциклист начал прохождение первого отрезка из состояния покоя. Изменения скорости мотоциклиста при прохождении им рассматриваемых отрезков пути можно записать как

 

78

 

Решения задач

 

 

1     1 1

∆v = a t , ∆v2 = a2t2 .

 

t

Выразив отсюда 1 , t2 и подставив их в формулы для перемещения мо-тоциклиста, получим соотношение:

 

2

1               1

=              +

.

a

∆v2   2∆v ∆v2  ∆v2 1              a2             a2

 

Отсюда легко определить искомое отношение ускорений:

 

∆

v

a

1

2

2

2

1

a1 = 2∆v ×∆v2 + ∆v2 = 0,8 .

 

 

l

2

7. Уравнение Эйнштейна для фотоэффекта имеет вид: hс = A+ m v2 ,

 

2

где h – постоянная Планка, l – длина волны света, A – работа выхода, m v2  – кинетическая энергия электрона, выбиваемого из металла. Из

 

этого уравнения следует, что максимальная длина волны l0 , при кото-рой ещё наблюдается фотоэффект (красная граница фотоэффекта), оп-ределяется равенством:

 

l

hc = A . 0

 

Если металлическому шарику сообщить заряд q , то квант света должен

 

передать электрону энергию, необходимую не только для совершения работы выхода, но и преодоления кулоновского притяжения электрона к заряженному шарику. Из закона сохранения энергии электрона, выбито-го с поверхности шарика, следует, что

 

2

m v2 = Eп ,

 

 

79

	E		=

 

 

Биологический факультет

 

 

 

где

qe

п   4pe0R

 

– приращение потенциальной энергии электрона при

 

его перемещении с поверхности шарика в бесконечно удаленную точку, e – модуль заряда электрона. Таким образом, в нашем случае уравнение

Эйнштейна приобретает вид:

 

=  +

,

hc hc   eq

 

l  l0    4pe0R

 

где l – максимальная длина волны падающего света, при которой вы-битые из шарика фотоэлектроны не будут возвращаться на него. Из по-следнего равенства получаем ответ:

 

l =

.

hc

 

hc/l0 +eq/4pe0R

 

 

T

8. На рис. 77 изображены силы, действующие на материальную точ-ку при максимальном отклонении математического маят-ника от положения равновесия. Поскольку скорость мате-риальной точки в этом положении равна нулю, то центро-стремительное ускорение также равно нулю. Поэтому сила натяжения нити 1 равна по модулю проекции силы тяже-сти на направление нити:

 

1

Рис. 77                                                 T = mgcosa .

При прохождении маятником положения равновесия, когда нить маятника занимает вертикальное положение, материальная точка обладает скоростью и, следовательно, центростремительным ускорени-ем. Из второго закона Ньютона, записанного для движения по окружно-сти, в проекции на ось, направленную вертикально вверх, следует урав-нение:

 

2

L

m v2 =T −mg ,

 

T

где 2 – натяжение нити в этом положении, v – скорость материальной точки, L – длина нити. При движении маятника от крайней точки к по-ложению равновесия происходит превращение потенциальной энергии

 

80

 

Решения задач

 

 

2

в кинетическую. Поэтому по закону сохранения механической энергии: mgh = m v2 ,

 

где h = L(1−cosa) – разница высот материальной точки в крайнем по-ложении и в нижней точке. Решая записанные выражения, находим:

2

T = mg + 2mg(1−cosa) .

 

3

ç     ÷

2        1

è     ø

Учитывая, что T = kT , получаем ответ: a = arccosæ k +2ö.

 

 

R

R

1

2

9. В электрической цепи, представленной в условии задачи, при ра-зомкнутом ключе K ток течет только через резистор  1 (конденсатор представляет собой разрыв электрической цепи, и ток через резистор 2 равен нулю). При замкнутом ключе внешняя цепь состоит из парал-лельно соединенных резисторов  R ,  R  и имеет сопротивление

 

R R

1 2

0

1     2

R = R + R . Полный ток во внешней цепи в обоих случаях:

 

E

E

r +

1 2

1

1     2

I1 = R + r , I2 =     R R . R + R

 

Приравнивая мощности, выделяющиеся во внешней цепи при разомк-нутом и замкнутом ключе K, имеем:

 

1

1 2

×

=

.

E2R               E2                    R R

 

R R

1     2

1

÷

ç

+

r

÷

ç

1     2

(r + R )2    æ       1 2  ö2  R + R è       R + R ø

 

2

r

1

2

2

1

Из решения этого уравнения получаем ответ: R = R R−r2 =1,3 Ом.

 

 

81

 

Биологический факультет

 

10. Работа, совершенная газом за цикл численно равна площади трапеции 1234 на pV–диаграмме:

 

1                                                         1

2

A = 1 (p − p4 + p2 − p3)(V2 −V ) .

 

Согласно уравнению Клапейрона-Менделеева для одного моля идеаль-ного газа имеем:

 

1 1         1

p V = RT .

 

Для изобарного процесса 3−4 по закону Гей-Люссака:

 

T

2     1

T

V =V 3 ; 4

 

для изохорного процесса 4 −1 по закону Шарля:

 

T

3      1

T

p = p  4 ; 3

 

2 2      1 1

для состояний 1 и 2 по закону Бойля-Мариотта: p V = p V .

 

Решая записанную систему уравнений, получаем ответ:

 

ö

æ

ö

ç

1               4      4      3

÷

ç

÷

ç

2       T  T  T

A = RT ç1− 2T + T ÷æT −1÷ » 625 Дж. è     1                 3 øè 4 ø

 

82

	=		.

 

 

Решения задач

 

ФАКУЛЬТЕТ ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКИ И КИБЕРНЕТИКИ

 

 

I. МЕХАНИКА

 

 

I.1. При упругом ударе о наклонную плоскость составляющая ско-рости шарика, параллельная плоскости, не изменяется, а составляющая, перпендикулярная плоскости, оставаясь

той же по величине, меняет направление на противопо-ложное. Следовательно, после удара шарик отскочит от наклонной плоскости со скоростью  v0   под углом = p −2a к горизонту. Кинематические уравнения дви-

 

жения шарика в системе координат, изображенной на рис. 78, имеют вид:

2

x = v0 cos ×t , y = −v0 sinb×t + gt2 .                         Рис. 78

 

В точке падения шарика на плоскость выполняются соотношения: x =l ,         y =ltga .

 

Исключая из записанных выражений время, получаем ответ:

 

 

v0 =

 

gl

 

2cos2(p −2a)[tga + tg(p −2a)]

glcosa 2sina |cos2a |

 

I.2. Траектория мяча, соответствующая максимальной скорости, удовлетворяющей условию задачи, изображена на рис. 79. При упругом ударе о стенку вертикальная составляющая скорости мяча не изменяет-ся, а горизонтальная, оставаясь той же по величине, меняет направление

 

83

	v =		.		x

 

 

Факультет ВМиК

 

 

на противоположное. Зависимость высоты мяча над поверхностью зем-ли имеет вид:

 

2

y = H +v0 sina ×t − gt2 .

 

Время полета мяча до ограждения

 

t =

.

L+l

 

0   v0 cosa

 

Рис. 79            Мяч не перелетит через ограждение, если y(t0) £ h . Исключая из записанных выражений время, получаем ответ:

 

L+l 0      cosa

 

g

2[(H −h)+(L+l)tga] » 7,17 м/с.

 

F

I.3. Лодка движется равномерно под действием двух сил: горизон-тальной составляющей силы натяжения веревки и силы сопротивления воды. Модули этих сил на рис. 80 обозначены через x и                                                 v0 , где b – ко-

 

 

Рис. 80

эффициент сопротивления воды. По второму закону Ньютона имеем: F =bv0 . Из рисунка видно, что F = F cosJ , где J – угол, который

 

x

веревка образует с горизонталью, причем

 

cosJ =      l0 −v0t     .

(l0 −v0t)2 + h2

 

Объединяя записанные равенства, получаем:

 

 

F = bv0

(l0 −v0t)2 + h2 l0 −v0t

 

0

Положив в последнем равенстве  t = 0 ,  F(0) = F ,  имеем:

 

84

	0				0		0		0		.

 

 

Решения задач

 

 

F =bv0  l2 +h2 , откуда bv0 = F 0

 

l0       .

l2 +h2

 

 

 

Ответ: F(t) = F    l0

l2 +h2

(l0 −v0t)2 +h2 l0 −v0t

 

0

Замечание: Из этой формулы видно, что по мере приближения лод-ки к пристани сила                                 неограниченно возрастает. Приведенный ответ имеет смысл до тех пор, пока F не превысит силу тяжести, действую-щую на лодку.

 

 

I.4. Брусок движется по горизонтальной окружности под действием сил, изображенных на рис. 81, где mg – сила тяжести,

 

N – нормальная составляющая силы реакции сферы, F – сила трения. В проекциях на оси OX и OY непод-

вижной координатной системы имеем:

 

mw 2Rcosa = N cosa − Fsina ,

 

F cosa + N sina −mg = 0 .                                      Рис. 81 Исключая отсюда N , находим

 

F = mcosa(g −w 2Rsina) .

 

Если угловая скорость вращения сферы такова, что w 2Rsina > g , то сила трения направлена противоположно. В общем случае ответ имеет вид: F = mcosa | g −w 2Rsina |.

 

 

I.5. На правую чашу весов, заполненную водой до краев, действует сила

 

F = Mg + N ,

 

 

85

 

Факультет ВМиК

 

 

где M = Sh – масса воды в этой чаше, N – сила давления падающих

 

капель дождя. Поскольку соударение капель с водой, находящейся в чаше, является неупругим, по второму закону Ньютона имеем:

 

∆m×v = (N −∆m×g)∆t ,

 

t

где ∆m = M ∆t – масса дождевых капель, попадающих в чашу за малое

 

время ∆t . Отсюда

 

t         t

N∆t = M v ∆t + Mg ∆t2 .

 

 

t

Учитывая малость ∆t , находим, что приближенно N » M v . Весы будут

 

 

F            N

уравновешены, если масса гири на левой чашеm = g =rSh+ g . Объе-

 

æ       ö

v

ç       ÷

è       ø

диняя записанные выражения, получаем ответ: m = rShç1+ gt÷ = 50,5 г.

 

I.6. В момент, когда достигается максимальное сжатие пружины, скорость бруска обращается в нуль. По закону изменения механической энергии имеем:

 

т

2

mgH = mg(l −∆l)sina + k∆l2 + A р ,

 

A                                                             F

т

H

ç                      ÷

è                      ø

где тр – модуль работы силы трения тр на перемещении бруска S , причем F р = µmgcosa , S =æsina −(l −∆l)ö . Следовательно,

 

H

÷

ç

т

ø

è

A р = µmgcosaæsina −(l −∆l)ö .

 

86

 

 

Решения задач

 

 

Объединяя записанные выражения, получаем квадратное уравнение относительно ∆l :

 

÷

ç

k                                      k                               in

ø

è

∆l2 − 2mg (sina −µcosa)∆l − 2mg (sina −µcosa)æsHa −lö = 0 .

 

Поскольку по условию задачи предоставленный самому себе брусок

 

H

приходит в движение, sina >µcosa . Кроме того, sina > l . Поэтому свободный член в квадратном уравнении заведомо отрицателен, и, сле-довательно, корни этого уравнения существуют. Условию задачи удов-летворяет положительный корень. Ответ:

 

 

ì

ï

í

k

ï

∆l = mg (sina −µcosa) 1+ î

2k       (H −lsina) ü

 

þ

mgsina (sina −µcosa) ï

 

I.7. Шарики находятся в равновесии под действием сил, модули и направления которых изображены на рис. 82, где

mg – модуль силы тяжести. В проекции на гори-

 

зонтальное и вертикальное направления условия равновесия шариков имеют вид:

 

T

2

T

2

1 sina =T sinb ,     1 cosa = mg +T cos ,

 

T

3

T

2 sinb =T ,    2 cos = mg .                                 Рис. 82

 

Отсюда вытекают следующие равенства:

 

T

T

1       2                                                     2

1 cosa = 2 2 cos ,  T2 =T2(sin2 b +4cos2 b) =T2(4−3sin2 b) .

 

T

4

2      1

Из последнего равенства находим 2 sinb = ( T2 −T2)/3 . Ответ:

 

3

4

2      1

T = ( T2 −T2)/3 .

 

 

87

 

Факультет ВМиК

 

I.9. Стакан будет находиться под водой в безразличном равновесии при выполнении условия

 

mg = rVg ,

 

r

где V – объем воздуха в стакане. Отсюда V = m . По закону Бойля-

 

Мариотта

 

0 0

p V = pV ,

 

где p = p0 +rgh – давление воды на глубине h . Объединяя записанные выражения, находим

 

p

0

0

h = rgm(rV −m) .

 

При меньшей глубине погружения предоставленный самому себе ста-кан будет всплывать. Наоборот, при увеличении глубины погружения стакан начнет опускаться вниз, так как с ростом давления воды вытал-

 

p

0

0

кивающая сила будет уменьшаться. Ответ: h ³ rgm (rV −m) =10 м.

 

 

*I.9. Пусть p – давление, создаваемое насосом, v – скорость воды в шланге. Согласно уравнению Бернулли,

2

p =rgh+ rv2 .

 

æ

Работа ∆A = p∆V , совершаемая насосом по перемещению воды объе-мом ∆V = S v∆t , равна

÷

ç

÷

2

∆A=rçgh+ v2 öS v∆t . è               ø

 

V

По условию V = S vt, откуда v = St . Объединяя записанные выраже-

 

 

88

 

Решения задач

 

 

2

ç

÷

ç

÷

t

∆

S t

è

ø

ния и учитывая, что N = ∆A , получаем ответ: N = rV ægh+ 2V2 2 ö .

 

I.10. По закону сложения ускорений ускорение свободного падения относительно системы отсчета, связанной с вагоном,

g1 = g −a. Из рис. 83 видно, что модуль этого ускоре-

 

1

g

ния равен g = a2 + g2 , а само ускорение образует с вертикалью угол a , причем tga = a . Следовательно, в

 

Рис. 83

момент начала движения вагона маятник оказывается отклоненным от устойчивого положения равновесия на угол a . В результате возникших колебаний макси-

мальный угол отклонения маятника от вертикали составит 2a . Как

 

видно из рисунка, h = l(1−cos2a) = 2lsin2 a . Используя формулу

 

2

a

2

+

+

t

sina = 1 tgg2 a , получаем ответ: h = g2la a2 .