Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

(РИСК-МЕНЕДЖМЕНТ)

________________________________________________________________

наименование учебной дисциплины (модуля)

Направление подготовки – 38.03.02 Менеджмент

Профиль подготовки – Управление малым бизнесом

Квалификация (степень) выпускника – бакалавр

Форма обучения – очная (заочная)

Воронеж 2019

Методические указания по решению задач по дисциплине «Управление рисками и страхование» (Риск-менеджмент) разработаны в соответствии с ФГОС ВО и ОПОП ВО по направлению подготовки – 38.03.02 Менеджмент, профиль подготовки – Управление малым бизнесом, квалификация (степень) выпускника __бакалавр__

 

 

Разработчик: С.Г. Борисова _____ВИВТ,___ доцент ___ _________________

(инициалы, фамилия    занимаемая должность) (место для подписи)

 

 

Методические указания по решению задач по дисциплине «Управление рисками и страхование» (Риск-менеджмент) рассмотрены на заседании Учебно-методического совета протокол № ___ от _____ ____________ 2019 г. и рекомендованы к использованию.

 

Председатель УМС ВИВТ                                                               С.М. Шляхова

Тема 3. Оценка рисков

Практические задания по теме

Статистические методы оценки рисков

Задача 1.1

В таблице 1.1 представлены данные по объемам реализации компании. Рассчитайте вероятность каждого значения временного ряда, а также следующие показатели его динамики:

1) размах вариации;

2) математическое ожидание;

3) дисперсия;

4) среднеквадратическое отклонение;

5) коэффициент вариации.

 

Таблица 1.1 — Объем реализации компании в стоимостном выражении

Показатель	Месяцы
	янв	фев	мар	апр	май	июн	июл	авг
Объем реализации, тыс. у.е.	120	115	135	120	158	115	100	120

 

Решение:

1) Размах вариации рассчитаем по формуле: R = X_max - X_min

R = 158 – 100 = 58

Таким образом, за указанный период разница между минимальным и максимальным значением объема реализации составила 58 тыс. у.е.

Но этот показатель дает очень грубую оценку риску, т.к. он является абсолютным показателем и зависит только от крайних значений ряда.

2) Математическое ожидание определим по формуле: M ( E ) = ∑(Х _k × Р _k )

Для расчета вероятности каждого значения выпишем все значения ряда без повторений. Для удобства расчетов составим таблицу (см. таблицу 1.2).

Рассчитаем вероятность каждого значения ряда по формуле: Р _k = k : N

Полученные результаты занесем в строку 1 таблицы 1.2.

Найдем произведение каждого значения и его вероятности. Результаты занесем в строку 2 таблицы 3.2.

Сумма полученных произведений является значением математического ожидания данного временного ряда: M ( E ) = 122,875

Математическое ожидание показывает наиболее правдоподобное значение объема реализации в месяц за указанный период.

3) Дисперсия временного ряда - мера разброса значений случайной величины относительно её математического ожидания и определяется по формуле: σ²(Ε) = ∑[( Х_k – M ( E ))² × Р _k )

Рассчитаем значение дисперсии поэтапно. Сначала найдем отклонение каждого значения ряда от среднего ожидаемого значения (строка 3 таблицы 1.2). Затем возведем в квадрат полученные значения отклонений (строка 4 таблицы 1.2). Наконец, умножим значения строки 4 на соответствующие значения вероятности (строка 5 таблицы 1.2). Сумма значений строки 5 представляет собой значение дисперсии данного временного ряда:

σ²(Ε) = 256,609

Использование дисперсии как меры риска не всегда удобно, т.к. размерность ее равна квадрату единицы измерения случайной величины.

Таблица 1.2 — Расчет статистических показателей

№ п/п

Показатели

Значения (Х k)

Итого

120

115

135

158

100

1

2

3

4

5

6

7

8

1

Вероятность (Р _k)

3:8 = 0,375

2:8 = 0,25

1:8= 0,125

1:8 = 0,125

1:8 = 0,125

1,0

2

Математическое ожидание

M ( E ) = ∑ ( Х _k × Р _k )

120×0,375 = 45

115×0,25 = 28,75

135×0,125 = 16,875

158×0,125 = 19,75

100×0,125 = 12,5

122,875

3

Х _k – M(E)

120 - 122,875 =

-2,875

115 – 122,875=

-7,875

135 – 122,875=

12,125

158 – 122,875=

35,125

100 – 122,875=

-22,875

-

( Х _k – M(E))²

8,266

62,016

147,016

1 233,766

523,266

-

Дисперсия

σ ² (Ε) = ∑ [ (Х _k – M ( E ))² × Р _k ) ]

8,266 × 0,375=

3,100

62,016 × 0,25=

15,504

147,016 × 0,125=

18,377

1 233,766 × 0,125=

154,221

523,266 × 0,125=

65,408

256,609

4

Стандартное (среднеквадратическое) отклонение

σ(Ε) = Ѵ¯σ²(Ε)

-

-

-

-

-

16,02

5

Коэффициент вариации

K_v = σ(Ε) : M ( E )

-

-

-

-

-

0,1304 (13,04 %)

 

4) Стандартное (среднеквадратическое) отклонение определим по формуле: σ(Ε) = Ѵ¯σ²(Ε).

σ(Ε) = 16,02

Таким образом, значение объема реализации за указанный период в среднем изменяется на 16,02 тыс. у.е. в месяц.

 

5) Коэффициент вариации, выраженный в процентах, показывает, насколько велики были отклонения параметров за анализируемый период. Рассчитаем значение коэффициента вариации по формуле: K_v = σ(Ε) : M ( E )

K_v = 16,02 : 122,875 = 0,1304 (т.е. 13,04 %).

Вывод:

Таким образом, значение объема реализации за указанный период изменяется в среднем на 13,04 %.

Совокупность стабильна, т.к. коэффициент вариации меньше 30 % (≤ 0,3).

 

2-ой вариант решения

Месяцы	Объем реализации, тыс. у.е. (Хi)	Хср = ∑Хi : n	Хi - Хср	(Хi - Хср) 2	σ2 = ∑ (Х k - Хср)2 : n	σ = V¯σ 2
1	2	3	4	5	6	7
Янв	120	983 : 8	-2,875	8,266	2 056,875 : 8	V¯256,609
Февр	115		7,875	62,016
Март	135		12,125	147,016
Апр	120		-2,875	8,266
Май	158		35,125	1233,766
Июнь	115		-7,875	62,016
Июль	100		-22,875	523,266
Авг	120		-2,875	8,266
Итого	983	122,875	-	2 056,875	256,609	16,019

5) Рассчитаем значение коэффициента вариации по формуле:

K_v = σ(Ε) : M ( E )

K_v = 16,02 : 122,875 = 0,1304 (т.е. 13,04 %)

 

 

2. Метод учета риска при расчете чистой приведенной стоимости NPV

Задача 2.1

(учет риска в знаменателе формулы NPV посредством корректировки ставки дисконта)

Первоначальные инвестиции компании в реализацию проекта составили 3 000 у.е.

Безрисковая дисконтная ставка составляет 10 %.

Плата за риск – 5 %.

Динамика чистых денежных потоков представлена в таблицу 2.1.

 

Таблица 2.1 — Динамика чистых денежных потоков

Показатель	Годы
	1	2	3	4	5
Стоимость чистого денежного потока, у.е.	1 100	2 200	2 000	-400	-1 000

 

Рассчитайте эффективность проекта с учетом и без учета риска.

 

Решение:

Для удобства расчетов составим таблицу 2.2.

Рассмотрим в таблице динамику денежных потоков по годам.

Для расчета дисконтированной стоимости денежных потоков воспользуемся формулой:

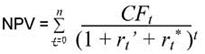
где, CF_t — чистый поток средств в год t,

r_t’ — безрисковая годовая ставка дисконта в год t,

r_t* — премия за риск в год t.

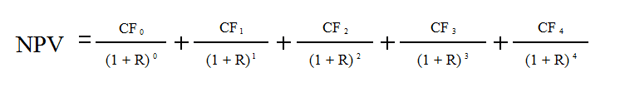
Дисконтирование – это метод определения будущей стоимости денежных потоков, т.е. приведение объема будущих доходов к настоящему моменту времени. Для того чтобы правильно оценить их величину, необходимо знать прогнозные значения выручки, расходов, вложений, структуру капитала и ставку дисконтирования, т.е. норму доходности на инвестируемый капитал.

Подробнее: http://www.kakprosto.ru/kak-89830-kak-rasschitat-stavku-diskontirovaniya#ixzz4YJZcwFHK Экономический смысл ставки дисконтирования https://otvet.mail.ru/question/16726417

 

Дисконтирование — это определение стоимости денежных потоков, относящихся к будущим периодам (будущих доходов на настоящий момент).

Для правильной оценки будущих доходов нужно знать

- прогнозные значения выручки,

- расходов, инвестиций,

- структуру капитала,

- остаточную стоимость имущества,

- а также ставку дисконтирования.

Ставка дисконтирования используется для оценки эффективности вложений. С экономической точки зрения ставка дисконтирования — это норма доходности на вложенный капитал, требуемая инвестором.

Иначе говоря, при помощи ставки дисконтирования можно определить сумму, которую инвестору придется заплатить сегодня за право получить предполагаемый доход в будущем. Поэтому от значения ставки дисконтирования зависит принятие ключевых решений, в том числе при выборе инвестиционного проекта.

 

Таблица 2.2 — Расчет чистой приведенной стоимости NPV проекта с учетом и без учета риска

Показатели	Годы						Сумма, тыс. у.е.
	0	1	2	3	4	5
1	2	3	4	5	6	7	8
Первоначальные инвестиции (I0), тыс. у.е.	3 000
Безрисковая годовая ставка дисконта rt', %		10	10	10	10	10
Премия за риск rt*, %		5	5	5	5	5
Годовая ставка дисконта с учетом премии за риск rt' + rt*, %		15	15	15	15	15
Чистые денежные потоки (CFt), тыс. у.е.		1 100	2 200	2 000	-400	-1 000
Приведенная стоимость чистых денежных потоков (без учета риска) PVt', тыс. у.е.		1 100:1,1 1 000,0	2 200:1,12 1 818,2	2 000:1,13 1 502,6	-400:1,14 -273,2	-1 000:1,15 -620,9	3 426,7
Приведенная стоимость чистых денежных потоков (с учетом риска) PVt*, тыс. у.е.		1 100:1,15 956,5	2 200:1,152 1 663,5	2 000:1,153 1 315,0	-400:1,154 -228,7	-1 000:1,15 -497,2	3 209,2
Чистая приведенная стоимость (NPV ') без учета риска, тыс. у.е.	426,7
Чистая приведенная стоимость (NPV*) с учетом риска, тыс. у.е.	209,2

 

Очевидно, что введение премии за риск существенно уменьшает чистую приведенную стоимость проекта, что является обоснованным: инвестор ждет более высокой прибыли от сделок, связанных с риском, чем от безрисковых вложений (например, таких как депозитный вклад в надежном банке).

Введение платы за риск также дает возможность сравнивать проекты с разным уровнем риска.

Задача 2.2

(учет риска в числителе формулы NPV посредством корректировки чистых денежных потоков)

 

Первоначальные инвестиции компании в реализацию проекта составили 3 000 у.е.

Безрисковая дисконтная ставка составляет 10 %.

Вероятность возникновения денежных потоков составляет 90 %.

Динамика чистых денежных потоков представлена в таблицу 2.1.

Рассчитайте эффективность проекта с учетом и без учета вероятности возникновения чистых денежных потоков.

Решение:

Для удобства расчетов составим таблицу 2.3.

Рассмотрим в таблице динамику денежных потоков по годам.

Для расчета дисконтированной стоимости денежных потоков воспользуемся формулой:

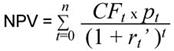
где, CF_t — чистый поток средств в год t,

p_t — вероятность возникновения потока CF_t в год t,

r_t ’ — безрисковая годовая ставка дисконта в год t.

Таблица 2.3 — Расчет чистой приведенной стоимости NPV проекта с учетом и без учета корректировки чистых денежных потоков

Показатели	Годы						Сумма, тыс. у.е.
	0	1	2	3	4	5
1	2	3	4	5	6	7	8
Первоначальные инвестиции (I0), тыс. у.е.	3 000
Безрисковая годовая ставка дисконта rt', %		10	10	10	10	10
Чистые денежные потоки (CFt), тыс. у.е.		1 100	2 200	2 000	-400	-1 000
Вероятность возникновения чистых денежных потоков (pt)		0,9	0,9	0,9	0,9	0,9
Стоимость денежных потоков с учетом вероятности (CFt × pt), тыс. у.е.		990	1 980	1 800	-360	-900
Приведенная стоимость денежных потоков без учета вероятности их возникновения (PVt), тыс. у.е.		1 100:1,1 1 000,0	2 200:1,12 1 818,2	1 502,6	-273,2	-620,9	3 426,7
Приведенная стоимость денежных потоков с учетом вероятности их возникновения (PVt*), тыс. у.е.		1 000×0,9 900,0	1 818,2×0,9 1 636,4	1 352,4	-245,9	-558,8	3 084,0
Чистая приведенная стоимость (NPV) без учета вероятности, тыс. у.е.	426,7
Чистая приведенная стоимость (NPV) с учетом вероятности, тыс. у.е.	84,0

 

 

Пример 1

Рассмотрим два условных проекта.

Оба проекта требуют начальных инвестиций в размере 500 р., другие затраты отсутствуют.

При реализации проекта «А» инвестор в течение трех лет получает в конце года доход в размере 500 р.

При реализации проекта «Б» инвестор получает доход в конце первого и в конце второго года по 300 р., а в конце третьего года — 1 100 р.

Инвестору нужно выбрать один из этих проектов.

 

Предположим, что инвестор определил ставку дисконтирования на уровне 25 % годовых.

Текущая стоимость (NPV) проектов «А» и «Б» рассчитывается следующим образом:

Год	Проекта «А»	Проекта «Б»
0	500	500
1	500	300
2	500	300
3	500	1 100

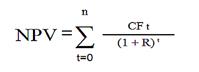
где P_k — денежные потоки за период с 1-го по n-й годы;

r — ставка дисконтирования — 25 %;

I — начальные инвестиции — 500 р.

Проект «А»

Показатели	Годы				Сумма, тыс. р.
	0	1	2	3
1	2	3	4	5	8
Первоначальные инвестиции (I0), р.	500
Безрисковая годовая ставка дисконта rt', %		25	25	25
Чистые денежные потоки (CFt), р.		500	500	500
Приведенная стоимость чистых денежных потоков (без учета риска) PVt', р.		400	320	256	976
Чистая приведенная стоимость (NPV'), р.	476

 

NPV(А) = [500 : (1 + 0,25)¹ + 500 : (1 + 0,25)² + 500 : (1 + 0,25)³] - 500 = 476 р.;

 

Проект «Б»

Показатели	Годы				Сумма, тыс. р.
	0	1	2	3
1	2	3	4	5	8
Первоначальные инвестиции (I0), р.	500
Безрисковая годовая ставка дисконта rt', %		25	25	25
Чистые денежные потоки (CFt), р.		300	300	1 100
Приведенная стоимость чистых денежных потоков (без учета риска) PVt', р.		240	192	563,2	995,2
Чистая приведенная стоимость (NPV'), р.	495,2

 

NPV(Б) = [300 : (1 + 0,25)¹ + 300 : (1 + 0,25)² + 1100 : (1 + 0,25)³] - 500 = 495,2 р.

Таким образом, инвестор выберет проект «Б».

 

Пример 2

Однако если он установит ставку дисконтирования, например, равную 35 % годовых, тогда текущие стоимости проектов «А» и «Б» будут равны 347,9 и 333,9 р. соответственно (расчет аналогичен предыдущему).

 

Проекта «А»

Показатели	Годы				Сумма, тыс. р.
	0	1	2	3
1	2	3	4	5	8
Первоначальные инвестиции (I0), р.	500
Безрисковая годовая ставка дисконта rt', %		35	35	35
Чистые денежные потоки (CFt), р.		500	500	500
Приведенная стоимость чистых денежных потоков (без учета риска) PVt', р.		370,4	274,3	203,2	847,9
Чистая приведенная стоимость (NPV'), р.	347,9

 

Проекта «Б»

Показатели	Годы				Сумма, тыс. р.
	0	1	2	3
1	2	3	4	5	6
Первоначальные инвестиции (I0), р.	500
Безрисковая годовая ставка дисконта rt', %		35	35	35
Чистые денежные потоки (CFt), р.		300	300	1 100
Приведенная стоимость чистых денежных потоков (без учета риска) PVt', р.		222,2	164,6	447,1	833,9
Чистая приведенная стоимость (NPV '), р.	333,9

 

Вывод:

В этом случае для инвестора проект «А» более предпочтителен.

Следовательно, решение инвестора полностью зависит от значения ставки дисконтирования: если она больше 30,28 % (при этом значении NPV(А) = NPV(Б)), то предпочтительнее проект «А», если меньше, тогда более выгодным будет проект «Б».

 

Существуют различные методы определения ставки дисконтирования.

 

Личное мнение

Ставка дисконтирования отражает стоимость денег с учетом временного фактора и рисков. Говоря о конкретном значении ставки дисконтирования, нельзя употреблять определения «правильная» или «неправильная», так как это всегда индивидуальная оценка.

Дискутировать имеет смысл о том, как она рассчитана, например на переговорах сторон о покупке или продаже какого-либо бизнеса, где значение ставки дисконтирования может повлиять на цену сделки.