МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО РЕШЕНИЮ ЗАДАЧ
ПО ДИСЦИПЛИН Е
УПРАВЛЕНИЕ РИСКАМИ И СТРАХОВАНИЕ
(РИСК-МЕНЕДЖМЕНТ)
________________________________________________________________
наименование учебной дисциплины (модуля)
Направление подготовки – 38.03.02 Менеджмент
Профиль подготовки – Управление малым бизнесом
Квалификация (степень) выпускника – бакалавр
Форма обучения – очная (заочная)
Воронеж 2019
Методические указания по решению задач по дисциплине «Управление рисками и страхование» (Риск-менеджмент) разработаны в соответствии с ФГОС ВО и ОПОП ВО по направлению подготовки – 38.03.02 Менеджмент, профиль подготовки – Управление малым бизнесом, квалификация (степень) выпускника __бакалавр__
Разработчик: С.Г. Борисова _____ВИВТ,___ доцент ___ _________________
(инициалы, фамилия занимаемая должность) (место для подписи)
Методические указания по решению задач по дисциплине «Управление рисками и страхование» (Риск-менеджмент) рассмотрены на заседании Учебно-методического совета протокол № ___ от _____ ____________ 2019 г. и рекомендованы к использованию.
Председатель УМС ВИВТ С.М. Шляхова
Тема 3. Оценка рисков
Практические задания по теме
Статистические методы оценки рисков
Задача 1.1
В таблице 1.1 представлены данные по объемам реализации компании. Рассчитайте вероятность каждого значения временного ряда, а также следующие показатели его динамики:
1) размах вариации;
2) математическое ожидание;
3) дисперсия;
4) среднеквадратическое отклонение;
5) коэффициент вариации.
Таблица 1.1 — Объем реализации компании в стоимостном выражении
| Показатель | Месяцы | |||||||
| янв | фев | мар | апр | май | июн | июл | авг | |
| Объем реализации, тыс. у.е. | 120 | 115 | 135 | 120 | 158 | 115 | 100 | 120 |
Решение:
1) Размах вариации рассчитаем по формуле: R = Xmax - Xmin
R = 158 – 100 = 58
Таким образом, за указанный период разница между минимальным и максимальным значением объема реализации составила 58 тыс. у.е.
Но этот показатель дает очень грубую оценку риску, т.к. он является абсолютным показателем и зависит только от крайних значений ряда.
2) Математическое ожидание определим по формуле: M ( E ) = ∑(Х k × Р k )
Для расчета вероятности каждого значения выпишем все значения ряда без повторений. Для удобства расчетов составим таблицу (см. таблицу 1.2).
Рассчитаем вероятность каждого значения ряда по формуле: Р k = k : N
Полученные результаты занесем в строку 1 таблицы 1.2.
Найдем произведение каждого значения и его вероятности. Результаты занесем в строку 2 таблицы 3.2.
Сумма полученных произведений является значением математического ожидания данного временного ряда: M ( E ) = 122,875
Математическое ожидание показывает наиболее правдоподобное значение объема реализации в месяц за указанный период.
3) Дисперсия временного ряда - мера разброса значений случайной величины относительно её математического ожидания и определяется по формуле: σ2(Ε) = ∑[( Хk – M ( E ))2 × Р k )
Рассчитаем значение дисперсии поэтапно. Сначала найдем отклонение каждого значения ряда от среднего ожидаемого значения (строка 3 таблицы 1.2). Затем возведем в квадрат полученные значения отклонений (строка 4 таблицы 1.2). Наконец, умножим значения строки 4 на соответствующие значения вероятности (строка 5 таблицы 1.2). Сумма значений строки 5 представляет собой значение дисперсии данного временного ряда:
σ2(Ε) = 256,609
Использование дисперсии как меры риска не всегда удобно, т.к. размерность ее равна квадрату единицы измерения случайной величины.
Таблица 1.2 — Расчет статистических показателей
| № п/п | Показатели | Значения (Х k) | |||||
Итого
120
115
135
158
100
2
3
4
5
6
7
8
Вероятность (Р k)
3:8 = 0,375
2:8 = 0,25
1:8= 0,125
1:8 = 0,125
1:8 = 0,125
1,0
Математическое ожидание
M ( E ) = ∑ ( Х k × Р k )
120×0,375 = 45
115×0,25 = 28,75
135×0,125 = 16,875
158×0,125 = 19,75
100×0,125 = 12,5
122,875
3
Х k – M(E)
120 - 122,875 =
-2,875
115 – 122,875=
-7,875
135 – 122,875=
12,125
158 – 122,875=
35,125
100 – 122,875=
-22,875
-
( Х k – M(E))2
8,266
62,016
147,016
1 233,766
523,266
-
Дисперсия
σ 2 (Ε) = ∑ [ (Х k – M ( E ))2 × Р k ) ]
8,266 × 0,375=
3,100
62,016 × 0,25=
15,504
147,016 × 0,125=
18,377
1 233,766 × 0,125=
154,221
523,266 × 0,125=
65,408
256,609
Стандартное (среднеквадратическое) отклонение
σ(Ε) = Ѵ¯σ2(Ε)
-
-
-
-
-
16,02
Коэффициент вариации
Kv = σ(Ε) : M ( E )
-
-
-
-
-
0,1304 (13,04 %)
4) Стандартное (среднеквадратическое) отклонение определим по формуле: σ(Ε) = Ѵ¯σ2(Ε).
σ(Ε) = 16,02
Таким образом, значение объема реализации за указанный период в среднем изменяется на 16,02 тыс. у.е. в месяц.
5) Коэффициент вариации, выраженный в процентах, показывает, насколько велики были отклонения параметров за анализируемый период. Рассчитаем значение коэффициента вариации по формуле: Kv = σ(Ε) : M ( E )
Kv = 16,02 : 122,875 = 0,1304 (т.е. 13,04 %).
Вывод:
Таким образом, значение объема реализации за указанный период изменяется в среднем на 13,04 %.
Совокупность стабильна, т.к. коэффициент вариации меньше 30 % (≤ 0,3).
2-ой вариант решения
| Месяцы | Объем реализации, тыс. у.е. (Хi) | Хср = ∑Хi : n | Хi - Хср | (Хi - Хср) 2 | σ2 = ∑ (Х k - Хср)2 : n | σ = V¯σ 2 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Янв | 120 | 983 : 8 | -2,875 | 8,266 | 2 056,875 : 8 | V¯256,609 |
| Февр | 115 | 7,875 | 62,016 | |||
| Март | 135 | 12,125 | 147,016 | |||
| Апр | 120 | -2,875 | 8,266 | |||
| Май | 158 | 35,125 | 1233,766 | |||
| Июнь | 115 | -7,875 | 62,016 | |||
| Июль | 100 | -22,875 | 523,266 | |||
| Авг | 120 | -2,875 | 8,266 | |||
| Итого | 983 | 122,875 | - | 2 056,875 | 256,609 | 16,019 |
5) Рассчитаем значение коэффициента вариации по формуле:
Kv = σ(Ε) : M ( E )
Kv = 16,02 : 122,875 = 0,1304 (т.е. 13,04 %)
2. Метод учета риска при расчете чистой приведенной стоимости NPV
Задача 2.1
(учет риска в знаменателе формулы NPV посредством корректировки ставки дисконта)
Первоначальные инвестиции компании в реализацию проекта составили 3 000 у.е.
Безрисковая дисконтная ставка составляет 10 %.
Плата за риск – 5 %.
Динамика чистых денежных потоков представлена в таблицу 2.1.
Таблица 2.1 — Динамика чистых денежных потоков
| Показатель | Годы | ||||
| 1 | 2 | 3 | 4 | 5 | |
| Стоимость чистого денежного потока, у.е. | 1 100 | 2 200 | 2 000 | -400 | -1 000 |
Рассчитайте эффективность проекта с учетом и без учета риска.
Решение:
Для удобства расчетов составим таблицу 2.2.
Рассмотрим в таблице динамику денежных потоков по годам.
Для расчета дисконтированной стоимости денежных потоков воспользуемся формулой:
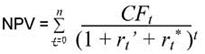
где, CFt — чистый поток средств в год t,
rt’ — безрисковая годовая ставка дисконта в год t,
rt* — премия за риск в год t.
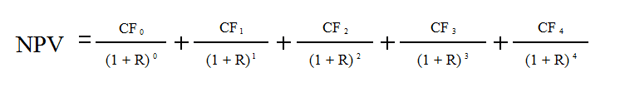
Дисконтирование – это метод определения будущей стоимости денежных потоков, т.е. приведение объема будущих доходов к настоящему моменту времени. Для того чтобы правильно оценить их величину, необходимо знать прогнозные значения выручки, расходов, вложений, структуру капитала и ставку дисконтирования, т.е. норму доходности на инвестируемый капитал.
Подробнее: http://www.kakprosto.ru/kak-89830-kak-rasschitat-stavku-diskontirovaniya#ixzz4YJZcwFHK Экономический смысл ставки дисконтирования https://otvet.mail.ru/question/16726417
Дисконтирование — это определение стоимости денежных потоков, относящихся к будущим периодам (будущих доходов на настоящий момент).
Для правильной оценки будущих доходов нужно знать
- прогнозные значения выручки,
- расходов, инвестиций,
- структуру капитала,
- остаточную стоимость имущества,
- а также ставку дисконтирования.
Ставка дисконтирования используется для оценки эффективности вложений. С экономической точки зрения ставка дисконтирования — это норма доходности на вложенный капитал, требуемая инвестором.
Иначе говоря, при помощи ставки дисконтирования можно определить сумму, которую инвестору придется заплатить сегодня за право получить предполагаемый доход в будущем. Поэтому от значения ставки дисконтирования зависит принятие ключевых решений, в том числе при выборе инвестиционного проекта.
Таблица 2.2 — Расчет чистой приведенной стоимости NPV проекта с учетом и без учета риска
| Показатели | Годы | Сумма, тыс. у.е. | |||||
| 0 | 1 | 2 | 3 | 4 | 5 | ||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Первоначальные инвестиции (I0), тыс. у.е. | 3 000 | ||||||
| Безрисковая годовая ставка дисконта rt', % | 10 | 10 | 10 | 10 | 10 | ||
| Премия за риск rt*, % | 5 | 5 | 5 | 5 | 5 | ||
| Годовая ставка дисконта с учетом премии за риск rt' + rt*, % | 15 | 15 | 15 | 15 | 15 | ||
| Чистые денежные потоки (CFt), тыс. у.е. | 1 100 | 2 200 | 2 000 | -400 | -1 000 | ||
| Приведенная стоимость чистых денежных потоков (без учета риска) PVt', тыс. у.е. | 1 100:1,1 1 000,0 | 2 200:1,12 1 818,2 | 2 000:1,13 1 502,6 | -400:1,14 -273,2 | -1 000:1,15 -620,9 | 3 426,7 | |
| Приведенная стоимость чистых денежных потоков (с учетом риска) PVt*, тыс. у.е. | 1 100:1,15 956,5 | 2 200:1,152 1 663,5 | 2 000:1,153 1 315,0 | -400:1,154 -228,7 | -1 000:1,15 -497,2 | 3 209,2 | |
| Чистая приведенная стоимость (NPV ') без учета риска, тыс. у.е. | 426,7 | ||||||
| Чистая приведенная стоимость (NPV*) с учетом риска, тыс. у.е. | 209,2 | ||||||
Очевидно, что введение премии за риск существенно уменьшает чистую приведенную стоимость проекта, что является обоснованным: инвестор ждет более высокой прибыли от сделок, связанных с риском, чем от безрисковых вложений (например, таких как депозитный вклад в надежном банке).
Введение платы за риск также дает возможность сравнивать проекты с разным уровнем риска.
Задача 2.2
(учет риска в числителе формулы NPV посредством корректировки чистых денежных потоков)
Первоначальные инвестиции компании в реализацию проекта составили 3 000 у.е.
Безрисковая дисконтная ставка составляет 10 %.
Вероятность возникновения денежных потоков составляет 90 %.
Динамика чистых денежных потоков представлена в таблицу 2.1.
Рассчитайте эффективность проекта с учетом и без учета вероятности возникновения чистых денежных потоков.
Решение:
Для удобства расчетов составим таблицу 2.3.
Рассмотрим в таблице динамику денежных потоков по годам.
Для расчета дисконтированной стоимости денежных потоков воспользуемся формулой:
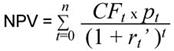
где, CFt — чистый поток средств в год t,
pt — вероятность возникновения потока CFt в год t,
rt ’ — безрисковая годовая ставка дисконта в год t.
Таблица 2.3 — Расчет чистой приведенной стоимости NPV проекта с учетом и без учета корректировки чистых денежных потоков
| Показатели | Годы | Сумма, тыс. у.е. | |||||
| 0 | 1 | 2 | 3 | 4 | 5 | ||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Первоначальные инвестиции (I0), тыс. у.е. | 3 000 | ||||||
| Безрисковая годовая ставка дисконта rt', % | 10 | 10 | 10 | 10 | 10 | ||
| Чистые денежные потоки (CFt), тыс. у.е. | 1 100 | 2 200 | 2 000 | -400 | -1 000 | ||
| Вероятность возникновения чистых денежных потоков (pt) | 0,9 | 0,9 | 0,9 | 0,9 | 0,9 | ||
| Стоимость денежных потоков с учетом вероятности (CFt × pt), тыс. у.е. | 990 | 1 980 | 1 800 | -360 | -900 | ||
| Приведенная стоимость денежных потоков без учета вероятности их возникновения (PVt), тыс. у.е. | 1 100:1,1 1 000,0 | 2 200:1,12 1 818,2 | 1 502,6 | -273,2 | -620,9 | 3 426,7 | |
| Приведенная стоимость денежных потоков с учетом вероятности их возникновения (PVt*), тыс. у.е. | 1 000×0,9 900,0 | 1 818,2×0,9 1 636,4 | 1 352,4 | -245,9 | -558,8 | 3 084,0 | |
| Чистая приведенная стоимость (NPV) без учета вероятности, тыс. у.е. | 426,7 | ||||||
| Чистая приведенная стоимость (NPV) с учетом вероятности, тыс. у.е. | 84,0 | ||||||
Пример 1
Рассмотрим два условных проекта.
Оба проекта требуют начальных инвестиций в размере 500 р., другие затраты отсутствуют.
При реализации проекта «А» инвестор в течение трех лет получает в конце года доход в размере 500 р.
При реализации проекта «Б» инвестор получает доход в конце первого и в конце второго года по 300 р., а в конце третьего года — 1 100 р.
Инвестору нужно выбрать один из этих проектов.
Предположим, что инвестор определил ставку дисконтирования на уровне 25 % годовых.
Текущая стоимость (NPV) проектов «А» и «Б» рассчитывается следующим образом:
| Год | Проекта «А» | Проекта «Б» |
| 0 | 500 | 500 |
| 1 | 500 | 300 |
| 2 | 500 | 300 |
| 3 | 500 | 1 100 |
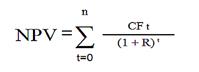
где Pk — денежные потоки за период с 1-го по n-й годы;
r — ставка дисконтирования — 25 %;
I — начальные инвестиции — 500 р.
Проект «А»
| Показатели | Годы | Сумма, тыс. р. | |||
| 0 | 1 | 2 | 3 | ||
| 1 | 2 | 3 | 4 | 5 | 8 |
| Первоначальные инвестиции (I0), р. | 500 | ||||
| Безрисковая годовая ставка дисконта rt', % | 25 | 25 | 25 | ||
| Чистые денежные потоки (CFt), р. | 500 | 500 | 500 | ||
| Приведенная стоимость чистых денежных потоков (без учета риска) PVt', р. | 400 | 320 | 256 | 976 | |
| Чистая приведенная стоимость (NPV'), р. | 476 | ||||
NPV(А) = [500 : (1 + 0,25)1 + 500 : (1 + 0,25)2 + 500 : (1 + 0,25)3] - 500 = 476 р.;
Проект «Б»
| Показатели | Годы | Сумма, тыс. р. | |||
| 0 | 1 | 2 | 3 | ||
| 1 | 2 | 3 | 4 | 5 | 8 |
| Первоначальные инвестиции (I0), р. | 500 | ||||
| Безрисковая годовая ставка дисконта rt', % | 25 | 25 | 25 | ||
| Чистые денежные потоки (CFt), р. | 300 | 300 | 1 100 | ||
| Приведенная стоимость чистых денежных потоков (без учета риска) PVt', р. | 240 | 192 | 563,2 | 995,2 | |
| Чистая приведенная стоимость (NPV'), р. | 495,2 | ||||
NPV(Б) = [300 : (1 + 0,25)1 + 300 : (1 + 0,25)2 + 1100 : (1 + 0,25)3] - 500 = 495,2 р.
Таким образом, инвестор выберет проект «Б».
Пример 2
Однако если он установит ставку дисконтирования, например, равную 35 % годовых, тогда текущие стоимости проектов «А» и «Б» будут равны 347,9 и 333,9 р. соответственно (расчет аналогичен предыдущему).
Проекта «А»
| Показатели | Годы | Сумма, тыс. р. | |||
| 0 | 1 | 2 | 3 | ||
| 1 | 2 | 3 | 4 | 5 | 8 |
| Первоначальные инвестиции (I0), р. | 500 | ||||
| Безрисковая годовая ставка дисконта rt', % | 35 | 35 | 35 | ||
| Чистые денежные потоки (CFt), р. | 500 | 500 | 500 | ||
| Приведенная стоимость чистых денежных потоков (без учета риска) PVt', р. | 370,4 | 274,3 | 203,2 | 847,9 | |
| Чистая приведенная стоимость (NPV'), р. | 347,9 | ||||
Проекта «Б»
| Показатели | Годы | Сумма, тыс. р. | |||
| 0 | 1 | 2 | 3 | ||
| 1 | 2 | 3 | 4 | 5 | 6 |
| Первоначальные инвестиции (I0), р. | 500 | ||||
| Безрисковая годовая ставка дисконта rt', % | 35 | 35 | 35 | ||
| Чистые денежные потоки (CFt), р. | 300 | 300 | 1 100 | ||
| Приведенная стоимость чистых денежных потоков (без учета риска) PVt', р. | 222,2 | 164,6 | 447,1 | 833,9 | |
| Чистая приведенная стоимость (NPV '), р. | 333,9 | ||||
Вывод:
В этом случае для инвестора проект «А» более предпочтителен.
Следовательно, решение инвестора полностью зависит от значения ставки дисконтирования: если она больше 30,28 % (при этом значении NPV(А) = NPV(Б)), то предпочтительнее проект «А», если меньше, тогда более выгодным будет проект «Б».
Существуют различные методы определения ставки дисконтирования.
Личное мнение
Ставка дисконтирования отражает стоимость денег с учетом временного фактора и рисков. Говоря о конкретном значении ставки дисконтирования, нельзя употреблять определения «правильная» или «неправильная», так как это всегда индивидуальная оценка.
Дискутировать имеет смысл о том, как она рассчитана, например на переговорах сторон о покупке или продаже какого-либо бизнеса, где значение ставки дисконтирования может повлиять на цену сделки.
Задача 3.1
Некая компания собирается инвестировать средства в производство роботов для использования в космических исследованиях. Инвестиции в данный проект производятся в три этапа.
1этап. В начальный момент времени t=0 необходимо потратить $ 500 тыс. долл. на проведение маркетингового исследования рынка. Менеджеры компании оценивают вероятность получения благоприятного результата в 80 %, и вероятность получения неблагоприятного результата в 20 %.
2 этап . Если в результате исследования будет выяснено, что потенциал рынка достаточно высок, то компания инвестирует еще $1 000 тыс. долл. на разработку и создание опытных образцов робота. Опытные образцы должны быть предложены к рассмотрению инженерам в центре космических исследований, которые решают вопрос о размещении заказа у данной компании. Менеджеры компании оценивают вероятность того, что в центре космических исследований воспримут такую модель благожелательно в 60 %, вероятность противоположного исхода в 40 % (что приведет к прекращению реализации проекта).
3 этап. Если реакция инженеров благоприятная, то в момент времени t=2 компания начинает строительство нового предприятия по производству данного робота. Строительство такого предприятия требует затрат в $10 000 тыс. долл. Если данная стадия будет реализована, то по оценкам менеджеров проект будет генерировать притоки наличности в течение четырех лет. Величина этих потоков наличности будет зависеть от того, насколько хорошо этот робот будет принят на рынке.
Вероятность того, что продукт будет хорошо “принят” рынком составляет 30 % и в этом случае чистые притоки наличности должны составлять около 10 000 тыс. долл. в год.
Вероятность того, что притоки наличности будут составлять около 4 000 тыс. долл. и 2 000 тыс. долл. в год, равна 40 % и 30 % соответственно.
Ставка цены капитала компании при реализации данного проекта составляет 11,5 %.
Постройте дерево решений, рассчитайте финансовый результат каждого варианта и определите целесообразность реализации проекта.
Решение:
Решение задачи начнем с построения дерева решений (рисунок 1).
Отметим на рисунке ключевые состояния, в которых возникают неопределенные варианты развития событий, каждому варианту припишем его денежную и вероятностную оценки.
Далее рассчитаем чистую приведенную стоимость каждого варианта развития событий по формуле:
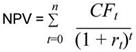
где, CFt — чистый поток средств в год t,
rt — годовая ставка дисконта в год t,
n — период прогнозирования.

Рисунок 1 — Дерево решений
Данные занесем в таблицу 3.1.
Затем найдем «совместную» вероятность каждого из вариантов. Согласно представленному рисунку вероятность 1 варианта составит:
р1 = 0,8 × 0,6 × 0,3 = 0,144
Аналогично рассчитаем вероятности остальных вариантов.
Имея значения доходности различных вариантов развития инвестиционного проекта и вероятностное распределение этих значений, можно рассчитать математическое ожидание доходности проекта (среднее ожидаемое значение).
Таблица 3.1 — Расчет совокупной эффективности проекта
| Показатели | Годы | |||||||
NPV
P
NPV×P
9
10
11
15 250,3
0,8 × 0,6 × 0,3
0,144
2 196,0
435,8
0,8 × 0,6 × 0,4
0,192
83,7
-4 502,3
-648,3
-1 396,9
0,8 × 0,3
0,320
-447,0
-500,0
0,200
-100,0
1084,4
Задача 3.2
Найти ветку поудобнее: изучаем дерево решений - http://gordo.st/skills/theory/theory_53.html
Дерево решений
Изучаем и применяем метод эффективного управления.
Нередко нам приходится принимать решения в условиях неопределенности, что называется «на свой страх и риск». Однако, если в повседневной жизни спонтанность допустима, то в бизнесе (под бизнесом имеется в виду любая организованная деятельность, нацеленная на результат) такое поведение будет считаться безответственным и, скорее всего, не приведёт нас к желаемой цели.
Практика показывает: чем сложнее управленческое решение, тем выше неопределенность его реализации. На это есть 4 причины:
1. Последствия принятия того или иного решения невозможно предсказать с высокой точностью.
(чем сложнее решение, тем ниже точность)
2. Существует в среднем не менее пяти-шести факторов, которые должны быть приняты во внимание при принятии решения.
(чем сложнее решение, тем больше факторов)
3. При подготовке решения нужно сократить неопределенность, собрав максимально возможное количество уточняющей информации.
(чем сложнее решение, тем больше информации)
4. Готовность руководителя к возможным рискам принятого решения влияет на количество альтернативных вариантов действий.
(чем сложнее решение, тем меньше альтернатив)
Но не думайте, что всё так сложно. На самом деле, поколения эффективных менеджеров проделали огромную работу, чтобы нам с вами было легче.
Для этого и существует методика дерева решений. Давайте разбираться.
В каких областях используется дерево решений?
- менеджмент,
- управление персоналом,
- экономика,
- финансы,
- прогнозирование рисков.
Как используется?
Если вдуматься в название метода, то суть "дерева решений" будет понятна без лишних разъяснений. Вспомнив о расходящихся ветвях обычного дерева, вы оказались правы. Вся соль и заключается в том, что данная методика предполагает разложение вариантов действий на разные составляющие с учётом последствий того или иного сценария. И цель его - сделать процесс реализации решения наиболее предсказуемым и учесть все «подводные камни».
Обычно деревья разбиваются на множество этапов, а зачастую включаются и промежуточные, чтобы не было возможности упустить важные детали или неблагоприятные последствия того или иного решения. После анализа всех ветвей выбирается и формулируется то решение, которое кажется наиболее выгодным и эффективным.
Польза данного метода в том, что очень часто при подробном анализе объективно лучшим оказывается совсем неочевидное решение.
Вам всё ещё кажется, что метод сложен и подвластен только магам?
Тогда посмотрите на это. Ничего не напоминает?
 Копить на
Копить на
 100 р.
100 р.
Попробовать
Да-да, вы всё правильно поняли, мы ещё с детства умеем составлять дерево решений! Так что, теперь осталось этот опыт перевести на рельсы реальных задач и проектов, запастись знаниями и отработать навык.
Как это выглядит?
Говоря простым языком, визуально дерево решений представляет собой иллюстрацию процесса принятия решений, выраженную в квадратиках, кружочках, стрелочках и черточках. На дереве всё - действия, последствия, альтернативные решения и этапы - находится на своем месте и следует друг за другом слева направо.
За десятилетия использования метода сложились определенные правила составления деревьев решений. Давайте с ними ознакомимся.
|
В квадратах пишутся решения
 |
А в кругах – их последствия
 Возможные решения обозначаются голубой линией
Возможные решения обозначаются голубой линией
 Возможные последствия – черной линией
Возможные последствия – черной линией
Товарищи, не любящие математику, для вас хорошая новость: при составлении дерева решений используется ВСЕГО ОДНА формула. Это стоимостная оценка каждого альтернативного решения.
Сравнение этих оценок и помогает выбрать самый выгодный вариант. Особенно полезно уметь делать такие расчёты всем, кто планирует работать в финансах и инвестиционной сфере и консалтинге.
Итак, что же за зверь эта стоимостная оценка?
Стоимостная оценка решения EMV – пронятое обозначение.
Считается EMV так: Цену выигрыша при возможном решении нужно умножить на вероятность исполнения этого возможного решения и сложить все оценки альтернатив. Выигрыш может быть и отрицательным.
Давайте рассмотрим простой пример.
Пример:
Вы можете вложить 300 тыс. р. в дело друга (магазин конной амуниции), который только начинает свой бизнес.
Если он окупиться через полгода, то Вы получите не только возврат инвестиций, но и еще 300 тыс. р. сверху.
То есть, выигрыш при таком решении может составить 600 тыс. р., вероятность успешного исхода дела составляет 60 %, то есть равна 0,6.
Теперь считаем стоимость такого исхода: 600 × 0,6 = 360 тыс. р.
Однако есть и вероятность в 40 %, что ничего из этой затеи не выйдет и Вы потеряете свои 300 тыс. р.
Считаем стоимость плохого исхода: [-300] × 0,4 = -120 тыс. р.
А теперь получаем EMV решения о вложение средств:
360 – 120 = 240 тыс. р.
Итак, наш EMV равен 240 тыс. р.
Сейчас вы обладаете базовыми знаниями, зачем, почему и как используется дерево решений. Давайте теперь построим новое дерево на основе предыдущего примера и немного расширим его.
Немного практики.
Представьте ситуацию: к вам приходит друг и говорит, что хочет открыть интернет-магазин по продаже конной амуниции. Он расписывает радужное будущее и утверждает, что в России такого больше нет. Но дело остается за малым: нужно вложить 500 тыс. р. на разработку сайта и закупку первой партии товаров.
У вашего друга есть только 200 тыс., а остальные он предлагает вложить вам, обещая, что, если магазин будет прибыльным, вернёт вам уже не 300, а 600 тыс. р.
Вас такое предложение, конечно, заинтересовало, но, понимая, что друг выбрал не совсем традиционную нишу для бизнеса, Вы предлагаете ему проверить гипотезу: сделать сайт-визитку и закупить небольшой ассортимент продукции. Всё это потребует вложений на 50 тыс. р. в тех же долях – 20 тыс. от друга и 30 тыс. от Вас.
И, если гипотеза подтвердится, Вы смело вложите и 300 тыс. р.
В конце встречи друг поделился с вами результатами своего анализа: вероятность того, что вложения в 300 тыс. р. окупятся, составляет 60 %, однако шансы на окупаемость пробных инвестиций в 30 тыс. р. – 50 %.
Также известно, что, если пробные инвестиции «прогорят», то вероятность выхода проекта на окупаемость после вложения 300 тыс. р. составляет всего 30 %. Есть еще и такой вариант: Вы сразу вкладываете 300 тыс. р., но в таком случае шансы на успех равны всего 20 %.
Вам нужно окончательно решить, стоит ли инвестировать в бизнес друга, и какая сумма вложений будет самой целесообразной.
За отправную точку вы взяли квадрат с названием «возможность вложить 300 тыс.» и разложили возможные решения на несколько ветвей.

 Получилось такое дерево. 240 600
Получилось такое дерево. 240 600

 240 Ок 0,6
240 Ок 0,6
|



 120 Ок 0 -300
120 Ок 0 -300


 120 0,5 0 Не вл 300 0
120 0,5 0 Не вл 300 0
|

|

 0,5 Вл 300 -30 600
0,5 Вл 300 -30 600

 Не вл Ок 0,3
Не вл Ок 0,3
 300 0 Н/о 0,7 -300
300 0 Н/о 0,7 -300
 Не ин -120
Не ин -120
 пр 30 0 Вл 300 0
пр 30 0 Вл 300 0



|
Н/о 0,8
 Не вл 300 0 -300
Не вл 300 0 -300
 0
0
Давайте подробно разберём его и поймём, откуда на дереве появились цифры.
Целые числа на концах линий означают цену исхода решения, то есть, сколько Вы можете заработать (положительное число) или потерять (отрицательное число), целые числа над кругами и квадратами - стоимостная оценка решения (та самая EMV), а десятичные дроби - это вероятности исходов, которые выше мы обозначили процентами.
Пронумерованные квадраты - это узлы решений.
Круги с буквами внутри - возможные исходы.
А теперь давайте считать:
В узле Е вероятность исхода «окупились равна 0,2, а не окупились – 0,8.
Первый исход приносит Вам прибыль в 600 тыс. р.», а второй – убыток в 300 тыс. р.
Вычислим оценки по формуле:
EMV [Е] = 0,2 × 600 + 0,8 × [-300] = -120 тыс. р.,
EMV [Ж] = 0.
Теперь узнаем стоимостную оценку узла решения 3.
Для этого выделяем максимальную оценку одного из исходов:
EMV [3] = max { EMV [Е]; EMV [Ж]} = max {-120; 0} = 0,
следовательно EMV [3] = 0
Если оценка равна 0, то решение не имеет смысла. Следовательно, все решения узла 3 отбрасываем.
Идем дальше. Все по аналогии.
EMV [Г] = 0,3 × 600 + 0,7 × [-300] = -30 max {-120; 0} = 0
EMV [Д] = 0.
EMV [2] = max {-30; 0} = 0 следовательно отбрасываем решение «вложить» в узле 2.
EMV [Б] = 0,6 × 600 + 0,4 × [-300] = 240 тыс. р.
EMV [В] = 0.
EMV [1] = max {240; 0} = 240 тыс. р.
Следовательно отбрасываем решение «не вложили» в узле 1.
EMV [А] = 0,5 × 240 + 0,5 × 0 = 120 тыс. р.
EMV [Возможности вложить 300 тыс. р.] = max {120; 0} = 120 тыс. р.
Отбрасываем возможное решение «не инвестируем пробные 30 тыс. р.»
И в результате: ожидаемая стоимостная оценка наилучшего решения = 120 тыс. р.
Что делать? Инвестируете пробные 30 тыс. р.
Если окупаются, вкладываете 300 тыс. р.
Если нет, то отказываетесь от участия в деле.
Вот и всё
Теперь вы знаете, как составлять дерево решений. Также важно отметить, что при применении этого метода не всегда нужно делать числовые расчеты, так как зачастую он используется и для решения качественных задач.
Для закрепления навыка попробуйте составить своё дерево решений.
А для простоты можете использовать аналогичный пример, подставив другие цифры и ситуации.
Задача 4
Первоначальные инвестиции (I 0) компании в реализацию проекта составили $30 000.
Норма дисконта (rt) по проекту составляет 10 %.
Постоянные затраты производства (FC) - $ 800 в год.
Переменные затраты на единицу продукции (vc) равны $ 8.
Планируемая цена реализации (P) – $ 20.
Объем реализации (Q) -1 200 шт.
Определите чувствительность NPV проекта к изменению цены, объема реализации, постоянных и переменных затрат на 10 %. Управлению каким из этих показателей компании необходимо уделить наибольшее внимание?
Рассчитайте критический объем производства без учета первоначальных инвестиций и дисконтирования.
Решение:
Рассчитаем базовое значение чистой приведенной стоимости проекта (NPV баз) в таблице 4.1.
Чистый денежный поток - это разница между положительным и отрицательным денежными потоками.
CFt = Xt - Yt
Положительный денежный поток (Х t) рассчитаем по формуле:
Х t = Q × P
Отрицательный денежный поток является суммой затрат на весь объем производства:
Yt = FC + Q × vc
Таблица 4.1 — Расчет базового значения чистой приведенной стоимости NPV
| Показатели | Годы | Сумма | |||||
| 0 | 1 | 2 | 3 | 4 | 5 | ||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Первоначальные инвестиции Iо | 30 000 | ||||||
| Норма дисконта rt, % | 10 | 10 | 10 | 10 | 10 | ||
| Положительный денежный поток Xt, $ | 20×1 200 24 000 | 24 000 | 24 000 | 24 000 | 24 000 | ||
| Отрицательный денежный поток Yt, $ | 800+8×1 200 10 400 | 10 400 | 10 400 | 10 400 | 10 400 | ||
| Чистый поток средств CFt, $ | 24 000-10 400 13 600 | 13 600 | 13 600 | 13 600 | 13 600 | ||
| Приведенная стоимость чистых денежных потоков PVt , $ | 13 600:1,1 12 363,6 | 13 600:1,12 11 239,7 | 13 600;1,13 10 217,9 | 13 600:1,14 9 289,0 | 13 600:1,15 8 444,5 | 51 554,7 | |
| Чистая приведенная стоимость NPV , $ | 21 554,7 | ||||||
Для определения чувствительности показателя эффективности (в данном случае NPV) к изменению исходных параметров проекта, необходимо выяснить, насколько изменится чистая приведенная стоимость при изменении (снижении или увеличении) этих исходных показателей (в данном случае – цены, объема реализации, постоянных и переменных затрат).
Изменим каждый из этих показателей на 10 % и выясним насколько изменится чистая приведенная стоимость NPV.
Выбор оптимальной стратегии
Задача 5
Минимальный гарантированно устойчивый спрос на продукцию предприятия составляет 100 шт.
Устойчивый сбыт на конкретный год составляет 200 шт.
Возможная сверх устойчивого спроса реализация составляет 300 шт.
Маловероятный, но потенциально возможный спрос составляет 400 шт.
Цена реализации продукции составляет (P) 5 у.е.
Постоянные расходы (FC) равны 250 у.е., переменные расходы на ед. продукции (vc) – 1 у.е.
Руководство предприятия планирует три стратегии производства продукции:
1) Q 1= 200 шт.,
2) Q 2= 300 шт.,
3) Q 3= 400 шт.
Определите оптимальную стратегию для данного предприятия на основе критерия Вальда, Сэвиджа и Гурвица. Выберите показатель Гурвица, близкий к оптимистическому сценарию.
Решение:
Определим значение прибыли (убытков) для каждого сочетания вариантов спроса (d) и объема производства (Q)
Прибыль рассчитаем как разницу между выручкой от реализации (В) и затратами (З):
П = В - З
Выручка от реализации при каждом варианте размера спроса определяется как произведение цены и объема реализации (спроса):
В = P × d
Затраты на производство продукции рассчитаем по формуле:
З = FC + vc × Q
Используйте таблицу 5.1а для расчета прибыли:
Таблица 5.1а — Расчет прибыли
| Стратегии производства продукции (Q) | Выручка от реализации В = d × P | Затраты на производство З = FC + vc × Q | Прибыль П = В - З |
| 100 Минимальный гарантированно устойчивый спрос | |||
| Q 1 =200 | 5×100 | 250 + 200×1 | 50 |
| Q 2 =300 | 5×100 | 250 + 300×1 | -50 |
| Q 3 =400 | 5×100 | 250 + 400×1 | -150 |
| 200 Устойчивый сбыт | |||
| Q 1 =200 | 5×200 | 250 + 200×1 | 550 |
| Q 2 =300 | 5×200 | 250 + 300×1 | 450 |
| Q 3 =400 | 5×200 | 250 + 400×1 | 350 |
| 300 Возможная сверх устойчивого спроса реализация | |||
| Q 1 =200 | 5×200 | 250 + 200×1 | 550 |
| Q 2 =300 | 5×300 | 250 + 300×1 | 950 |
| Q 3 =400 | 5×300 | 250 + 400×1 | 850 |
| 400 Маловероятный, но потенциально возможный спрос | |||
| Q 1 =200 | 5×200 | 250 + 200×1 | 550 |
| Q 2 =300 | 5×300 | 250 + 300×1 | 950 |
| Q 3 =400 | 5×400 | 250 + 400×1 | 1 350 |
Полученные данные занесем в таблицу 5.1 и определим максимальные и минимальные значения прибыли при различных вариантах объема производства, а также максимальные значения прибыли при каждом варианте объема спроса на продукцию.
Таблица 5.1 — Значения прибыли при различных вариантах объема производства и спроса на продукцию
|
| Спрос на продукцию (d) | ||||||
Пмин
Пмакс
Минимальный гарантированно устойчивый спрос
Устойчивый сбыт
Возможная сверх устойчивого спроса реализация
Маловероятный, но потенциально возможный спрос
100
200
300
400
Стратегии производства продукции (Q)
200
50
550
550
550
50
550
300
-50
450
950
950
-50
950
400
-150
350
850
1 350
-150
1 350
П макс
50
550
950
1 350
100
200
300
400
Стратегии производства продукции (Q)
200
50
550
550
550
550
300
-50
450
950
950
950
400
-150
350
850
1 350
1 350
Пмакс
50
550
950
1 350
Расчет значений показателя риска R при различных вариантах объема производства и спроса на продукцию осуществляется по формуле R = П max - Пij.
По этой формуле рассчитываем в таблице 5.2а показатель риска по данным таблицы 5.1 и заносим в таблицу 5.2.
Затем для каждой стратегии Q i выбираем максимальное значение показателя риска R max.
Таблица 5.2а — Расчёт значений показателя риска R при различных вариантах объема производства и спроса на продукцию
|
| Спрос на продукцию (d) | R max | |||||
| Минимальный гарантированно устойчивый спрос | Устойчивый сбыт | Возможная сверх устойчивого спроса реализация | Маловероятный, но потенциально возможный спрос | ||||
|
100 |
200 |
300 |
400 | ||||
| Стратегии производства продукции (Q) | Q 1 |
200 | 50-50= 0 | 550-550= 0 | 950-550= 400 | 1 350-550= 800 | 800 |
| Q 2 |
300 | 50-(-50)= 100 | 550-450= 100 | 950-950= 0 | 1 350-950= 400 | 400 | |
| Q 3 |
400 | 50-(-150)= 200 | 550-350= 200 | 950-850= 100 | 1 350-1 350= 0 | 200 | |
| Пмакс | 50 | 550 | 950 | 1 350 | |||
Таблица 5.2 — Значения показателя риска R при различных вариантах объема производства и спроса на продукцию
|
| Спрос на продукцию (d) | R max | |||||
| Минимальный гарантированно устойчивый спрос | Устойчивый сбыт | Возможная сверх устойчивого спроса реализация | Маловероятный, но потенциально возможный спрос | ||||
|
100 |
200 |
300 |
400 | ||||
| Стратегии производства продукции (Q) | Q 1 |
200 | 0 | 0 | 400 | 800 | 800 |
| Q 2 |
300 | 100 | 100 | 0 | 400 | 400 | |
| Q 3 |
400 | 200 | 200 | 100 | 0 |
200 | |
Показатель R max является основой минимаксного критерия Сэвиджа, согласно которому выбирается такая стратегия Q i, при которой величина Rmax принимает минимальное значение.
В нашем примере Q опт = Q 3 = 400 ед.
Сущность этого критерия в стремлении избежать большего риска в погоне за максимальной прибылью.
Вариант 0
(определяется по последней цифре номера зачетной книжки)
2 000
4 000
7 000
Выбор оптимальной стратегии
Минимальный гарантированно устойчивый спрос на продукцию предприятия составляет 20 шт. Устойчивый сбыт на конкретный год составляет 40 шт. Возможная сверх устойчивого спроса реализация составляет 50 шт. Маловероятный, но потенциально возможный спрос составляет 60 шт.
Цена реализации продукции составляет 14 у.е.
Постоянные расходы равны 120 у.е., переменные расходы на единицу продукции – 1,6 у.е.
Руководство предприятия планирует три стратегии производства продукции:
S1 = 40 шт.,
S2 = 50 шт.,
S3 = 60 шт.
Определите оптимальную стратегию для данного предприятия на основе критерия Вальда, Сэвиджа и Гурвица. Выберите показатель Гурвица, близкий к оптимистическому сценарию.
Вариант 1
(определяется по последней цифре номера зачетной книжки)
102
100
104
112
128
106
104
102
102
98
2. Метод учета риска при расчете чистой приведенной стоимости NPV
Первоначальные инвестиции компании в реализацию проекта составили 30 000 у.е. Безрисковая дисконтная ставка составляет 8 %. Плата за риск – 4 %. Динамика чистых денежных потоков представлена в таблице 2. Рассчитайте эффективность проекта с учетом и без учета риска. Опишите недостатки данного метода учета рисков.
Таблица 2
| Год | 1 | 2 | 3 | 4 | 5 |
| Стоимость денежного потока, у.е. |
24 000 | -22 000 | -16 000 |
28 000 |
32 000 |
Выбор оптимальной стратегии
Минимальный гарантированно устойчивый спрос на продукцию предприятия составляет 1 000 шт. Устойчивый сбыт на конкретный год составляет 2 000 шт. Возможная сверх устойчивого спроса реализация составляет 3 000 шт. Маловероятный, но потенциально возможный спрос составляет 4 000 шт.
Цена реализации продукции составляет 5 у.е.
Постоянные расходы равны 500 у.е., переменные расходы на единицу продукции – 1,1 у.е.
Руководство предприятия планирует три стратегии производства продукции:
S1 = 2 000 шт.,
S2 = 3 000 шт.,
S3 = 4 000 шт.
Определите оптимальную стратегию для данного предприятия на основе критерия Вальда, Сэвиджа и Гурвица. Выберите показатель Гурвица, близкий к оптимистическому сценарию.
Вариант 2
(определяется по последней цифре номера зачетной книжки)
22 000
34 000
48 000
Выбор оптимальной стратегии
Минимальный гарантированно устойчивый спрос на продукцию предприятия составляет 2 000 шт. Устойчивый сбыт на конкретный год составляет 4 000 шт. Возможная сверх устойчивого спроса реализация составляет 6 000 шт. Маловероятный, но потенциально возможный спрос составляет 8 000 шт.
Цена реализации продукции составляет 5 у.е.
Постоянные расходы равны 500 у.е., переменные расходы на единицу продукции – 1,5 у.е.
Руководство предприятия планирует три стратегии производства продукции:
S1 = 4 000 шт.,
S2 = 6 000 шт.,
S3 = 8 000 шт.
Определите оптимальную стратегию для данного предприятия на основе критерия Вальда, Сэвиджа и Гурвица. Выберите показатель Гурвица, близкий к пессимистическому сценарию.
Вариант 3
(определяется по последней цифре номера зачетной книжки)
12 000
18 000
26 000
Выбор оптимальной стратегии
Минимальный гарантированно устойчивый спрос на продукцию предприятия составляет 2 000 шт. Устойчивый сбыт на конкретный год составляет 3 000 шт. Возможная сверх устойчивого спроса реализация составляет 4 000 шт. Маловероятный, но потенциально возможный спрос составляет 5 000 шт.
Цена реализации продукции составляет 10 у.е.
Постоянные расходы равны 200 у.е., переменные расходы на единицу продукции – 4 у.е.
Руководство предприятия планирует три стратегии производства продукции:
S1 = 3 000 шт.
S2 = 4 000 шт.,
S3 = 5 000 шт.
Определите оптимальную стратегию для данного предприятия на основе критерия Вальда, Сэвиджа и Гурвица. Выберите показатель Гурвица, близкий к оптимистическому сценарию.
Вариант 4
(определяется по последней цифре номера зачетной книжки)
204
220
215
210
204
200
215
220
206
204
2. Метод учета риска при расчете чистой приведенной стоимости NPV
Первоначальные инвестиции компании в реализацию проекта составили 25 000 у.е. Безрисковая дисконтная ставка составляет 11 %. Вероятность возникновения денежных потоков составляет 90 %.
Динамика чистых денежных потоков представлена в таблице 2. Рассчитайте эффективность проекта с учетом и без учета риска. Опишите недостатки данного метода учета рисков.
Таблица 2
| Год | 1 | 2 | 3 | 4 | 5 |
| Стоимость денежного потока, у.е. | -22 000 | -6 000 |
22 000 |
28 000 |
32 000 |
Выбор оптимальной стратегии
Минимальный гарантированно устойчивый спрос на продукцию предприятия составляет 500 шт. Устойчивый сбыт на конкретный год составляет 1 000 шт. Возможная сверх устойчивого спроса реализация составляет 2 000 шт. Маловероятный, но потенциально возможный спрос составляет 4 000 шт.
Цена реализации продукции составляет 10 у.е.
Постоянные расходы равны 100 у.е., переменные расходы на единицу продукции – 2 у.е.
Руководство предприятия планирует три стратегии производства продукции:
S1 = 1 000 шт.,
S2 = 2 000 шт.,
S3 = 4 000 шт.
Определите оптимальную стратегию для данного предприятия на основе критерия Вальда, Сэвиджа и Гурвица. Выберите показатель Гурвица, близкий к пессимистическому сценарию.
Вариант 5
(определяется по последней цифре номера зачетной книжки)
3 000
5 000
6 000
Выбор оптимальной стратегии
Минимальный гарантированно устойчивый спрос на продукцию предприятия составляет 50 шт. Устойчивый сбыт на конкретный год составляет 80 шт. Возможная сверх устойчивого спроса реализация составляет 100 шт. Маловероятный, но потенциально возможный спрос составляет 150 шт.
Цена реализации продукции составляет 12 у.е.
Постоянные расходы равны 120 у.е., переменные расходы на единицу продукции – 3 у.е.
Руководство предприятия планирует три стратегии производства продукции:
S1 = 80 шт.,
S2 = 100 шт.,
S3 = 150 шт.
Определите оптимальную стратегию для данного предприятия на основе критерия Вальда, Сэвиджа и Гурвица. Выберите показатель Гурвица, близкий к оптимистическому сценарию.
Вариант 6
(определяется по последней цифре номера зачетной книжки)
8 000
14 000
20 000
Выбор оптимальной стратегии
Минимальный гарантированно устойчивый спрос на продукцию предприятия составляет 200 шт. Устойчивый сбыт на конкретный год составляет 350 шт. Возможная сверх устойчивого спроса реализация составляет 400 шт. Маловероятный, но потенциально возможный спрос составляет 500 шт.
Цена реализации продукции составляет 15 у.е.
Постоянные расходы равны 150 у.е., переменные расходы на единицу продукции - 4 у.е.
Руководство предприятия планирует три стратегии производства продукции:
S1 = 350 шт.,
S2 = 400 шт.,
S3 = 500 шт.
Определите оптимальную стратегию для данного предприятия на основе критерия Вальда, Сэвиджа и Гурвица. Выберите показатель Гурвица, близкий к пессимистическому сценарию.
Вариант 7
(определяется по последней цифре номера зачетной книжки)
1 000
1 000
2 000
2 000
Выбор оптимальной стратегии
Минимальный гарантированно устойчивый спрос на продукцию предприятия составляет 150 шт. Устойчивый сбыт на конкретный год составляет 200 шт. Возможная сверх устойчивого спроса реализация составляет 250 шт. Маловероятный, но потенциально возможный спрос составляет 300 шт.
Цена реализации продукции составляет 4 у.е.
Постоянные расходы равны 140 у.е., переменные расходы на единицу продукции – 1 у.е.
Руководство предприятия планирует три стратегии производства продукции:
S1 = 200 шт.,
S2 = 250 шт.,
S3 = 300 шт.
Определите оптимальную стратегию для данного предприятия на основе критерия Вальда, Сэвиджа и Гурвица. Выберите показатель Гурвица, близкий к оптимис тическому сценарию.
Вариант 8
(определяется по последней цифре номера зачетной книжки)
198
222
216
210
198
204
216
222
206
198
2. Метод учета риска при расчете чистой приведенной стоимости NPV
Первоначальные инвестиции компании в реализацию проекта составили 5 000 у.е. Безрисковая дисконтная ставка составляет 10 %. Вероятность возникновения денежных потоков составляет 90 %.
Динамика чистых денежных потоков представлена в таблице 2. Рассчитайте эффективность проекта с учетом и без учета риска. Опишите недостатки данного метода учета рисков.
Таблица 2
| Год | 1 | 2 | 3 | 4 | 5 |
| Стоимость денежного потока, у.е. | -8 000 | -2 000 |
7 000 |
8 000 |
10 000 |
Выбор оптимальной стратегии
Минимальный гарантированно устойчивый спрос на продукцию предприятия составляет 400 шт. Устойчивый сбыт на конкретный год составляет 500 шт. Возможная сверх устойчивого спроса реализация составляет 600 шт. Маловероятный, но потенциально возможный спрос составляет 700 шт.
Цена реализации продукции составляет 7 у.е.
Постоянные расходы равны 220 у.е., переменные расходы на единицу продукции – 3 у.е.
Руководство предприятия планирует три стратегии производства продукции:
S1 = 500 шт.,
S2 = 600 шт.,
S3 = 700 шт.
Определите оптимальную стратегию для данного предприятия на основе критерия Вальда, Сэвиджа и Гурвица. Выберите показатель Гурвица, близкий к пессимистическому сценарию.
Вариант 9
(определяется по последней цифре номера зачетной книжки)
150
170
162
150
168
200
162
170
206
168
2. Метод учета риска при расчете чистой приведенной стоимости NPV
Первоначальные инвестиции компании в реализацию проекта составили 3 000 у.е. Безрисковая дисконтная ставка составляет 8 %. Плата за риск – 2 %. Динамика чистых денежных потоков представлена в таблице 2. Рассчитайте эффективность проекта с учетом и без учета риска. Опишите недостатки данного метода учета рисков.
Таблица 2
| Год | 1 | 2 | 3 | 4 | 5 |
| Стоимость денежного потока, у.е. | -5 000 | -1 000 |
2 000 |
4 000 |
7 000 |
Выбор оптимальной стратегии
Минимальный гарантированно устойчивый спрос на продукцию предприятия составляет 110 шт. Устойчивый сбыт на конкретный год составляет 140 шт. Возможная сверх устойчивого спроса реализация составляет 150 шт. Маловероятный, но потенциально возможный спрос составляет 180 шт.
Цена реализации продукции составляет 9 у.е.
Постоянные расходы равны 250 у.е., переменные расходы на единицу продукции – 1,8 у.е.
Руководство предприятия планирует три стратегии производства продукции:
S1 = 140 шт.,
S2 = 150 шт.,
S3 = 180 шт.
Определите оптимальную стратегию для данного предприятия на основе критерия Вальда, Сэвиджа и Гурвица. Выберите показатель Гурвица, близкий к пессимистическому сценарию.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО РЕШЕНИЮ ЗАДАЧ
ПО ДИСЦИПЛИН Е
Дата: 2019-07-25, просмотров: 336.