Систему уравнений (4.1) будем решать асимптотическим методом марковизируемых систем [7] при .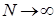

Первое приближение

В системе уравнений (4.1) сделаем следующие замены переменных: 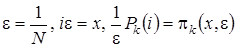. В результате такой замены производится переход от дискретной переменной  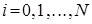к непрерывной переменной 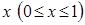. В новых обозначениях система (4.1) примет вид

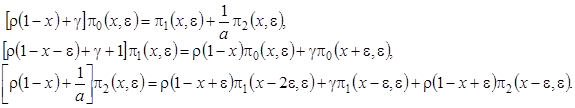(4.2)

    Получим вид решения системы (4.2), которую будем решать в два этапа.

1 этап . Устремим 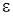 к нулю и обозначим 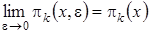. Тогда система (4.2) перейдет в систему

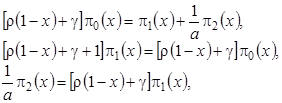                                 (4.3)

решение которой имеет вид

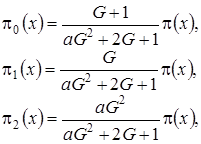                              (4.4)

где  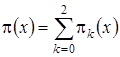– асимптотическая плотность распределения вероятностей нормированного числа заявок в ИПВ.

    Осталось найти вид функции 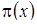, для этого перейдем ко второму этапу.

2 этап . В системе (4.2) все функции с аргументом 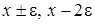 разложим в ряд по приращению аргумента 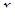, ограничиваясь слагаемыми порядка 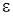, получим

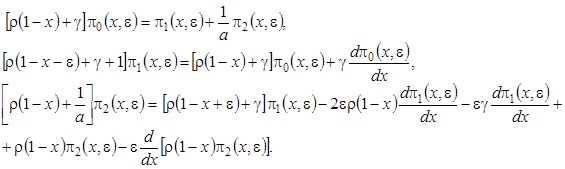(4.5)

Сложив все уравнения системы, будем иметь

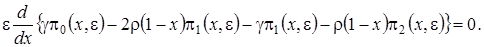  (4.6)

В полученном равенстве поделим левую и правую части на 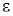 и 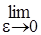, прейдем к такому равенству

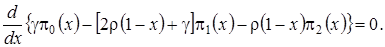            (4.7)

Подставим в (4.7) функции 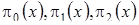 в форме (4.4) и получим

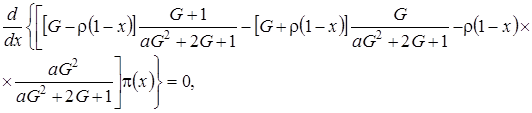(4.8)

следовательно

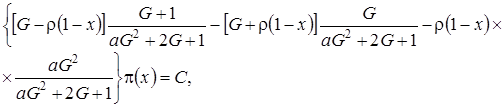(4.9)

где С – некоторая постоянная.

Необходимо найти константу C. Нетрудно заметить, что при х=0 выражение в фигурных скобках не положительно, следовательно 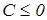, а при х=1 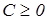. Итак, 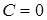. Таким образом, произведение двух функций равно нулю, следовательно,  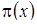может принимать какое-либо ненулевое значение лишь в тех точках, в которых выражение в скобках равно нулю.

Получим функцию 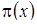, везде равную нулю, за исключением точек, являющихся корнями уравнения

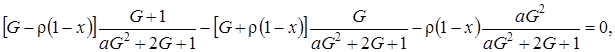
после преобразований это выражение принимает вид

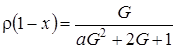                         (4.10)

    Так как 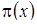 – плотность распределения вероятностей, то должно выполняться условие нормировки 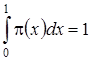. Этим условиям удовлетворяет лишь функция вида

,

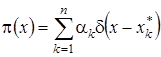где 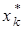– корни уравнения (4.10), n – число корней, .

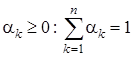    Если уравнение (4.10) имеет единственный корень 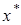, то эту точку назовем точкой стабилизации, потому что она является модой распределения вероятностей нормированного процесса заявок в ИПВ , и в ее окрестности достаточно долго флуктуируют значения этого процесса. В этом случае назовем сеть моностабильной.

Второе приближение

Пусть уравнение (4.10) имеет единственный корень 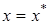, то есть плотность распределения исследуемой сети сосредоточена около точки 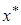. Найдем плотность распределения отклонения от этой точки. Для этого в системе (4.1) сделаем замену переменных: , , .

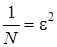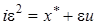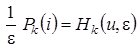В новых обозначениях система (4.1) примет вид

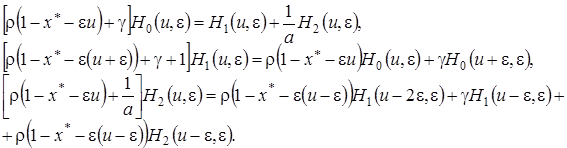(4.11)

Систему (4.11) будем решать в три этапа.

1 этап. Устремим  к нулю и обозначим 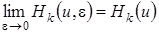, тогда система (4.11) перейдет в систему

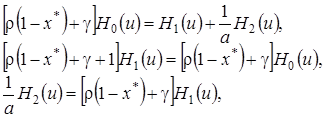               (4.12)

решение которой имеет вид

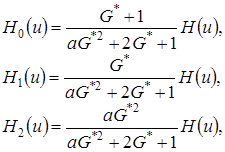                                   (4.13)

где 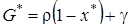,  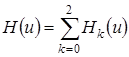– плотность распределения нормированной величины 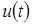отклонения процесса  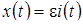от значения  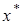– корня уравнения (4.10).

Найдем вид функции .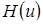

2 этап. Неизвестные функции 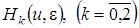 будем искать в форме

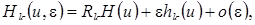                             (4.14)

где 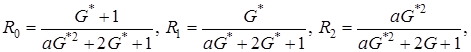         (4.15)

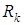 – асимптотическая вероятность того, что состояние обслуживающего канала равно .

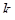В системе уравнений (4.11) все функции с аргументом 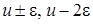 разложим в ряд по приращению аргумента 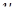, ограничиваясь слагаемыми порядка , получим

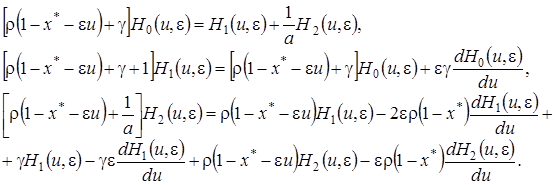(4.16)

В полученных формулах заменяем 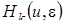 по формуле (4.14), при этом учитываем, что из системы (4.12) следуют равенства

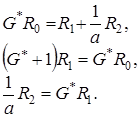                                 (4.17)

           Получим неоднородную линейную систему алгебраических уравнений относительно неизвестных функций 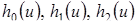 (в предположении, что  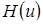известна) вида

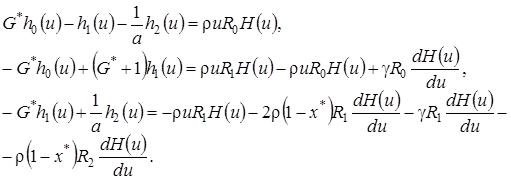      (4.18)

    Заметим, что ранг соответствующей однородной системы равен двум. Следовательно, для того, чтобы решение системы (4.18) существовало, необходимо, чтобы ранг расширенной матрицы этой системы также равнялся двум, т.е. чтобы выполнялось следующее равенство

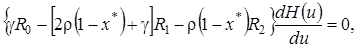                  (4.19)

откуда следует, что

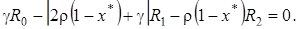                    (4.20)

Чтобы показать равенство (4.20) воспользуемся определением для 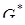 и свойствами констант 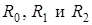, получим

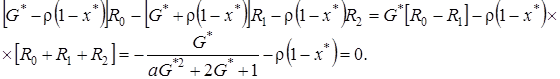(4.21)

Если предположить, что функция 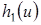 известна, то решение системы (4.18) примет вид

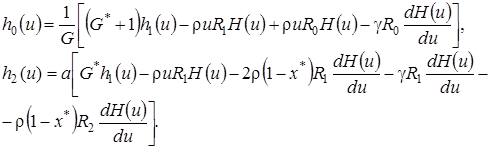          (4.22)

3 этап. В системе (4.11) все функции с аргументом 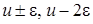 разложим в ряд по приращению аргумента 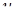, ограничиваясь слагаемыми порядка 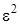, будем иметь

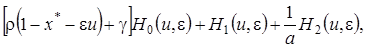
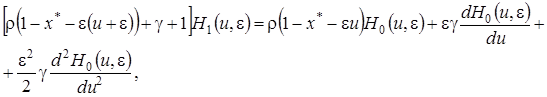(4.23)

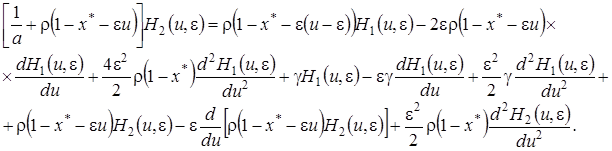
Сложив левые и правые части системы уравнений (4.23) получим

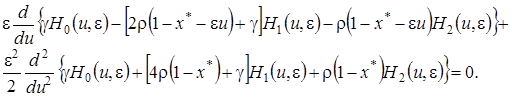     (4.24)

Чтобы сделать предельный переход в полученной формуле, нужно чтобы все слагаемые имели порядок 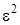. Заменим  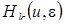по формуле (4.14), подставив вместо  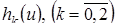их выражения, полученные на втором этапе. Для  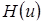получим линейное дифференциальное уравнение второго порядка вида

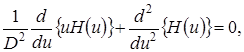                     (4.25)

где

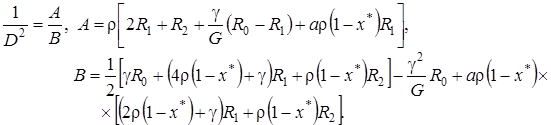(4.26)

Решение уравнения (4.25) можно найти в виде

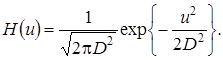                         (4.27)