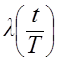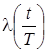|
, где Т – некоторый интервал времени, в течение которого функционирует сеть связи. Структура сети изображена на рис. 2.1.
 | |||||||||||||||
 | |||||||||||||||
 | |||||||||||||||
 | |||||||||||||||
 |  |  | |||||||||||||
 | |||||||||||||||
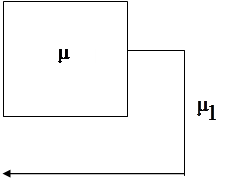
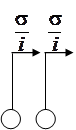
Рис. 2.1 – Модель системы массового обслуживания
В нестационарном режиме распределение
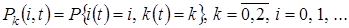
удовлетворяют системе дифференциально-разностных уравнений вида
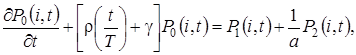
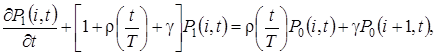(2.1)
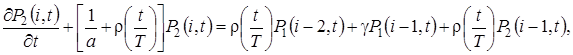
где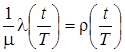 
, 
, 
, 
.
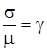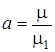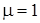Замечание: система уравнений (2.1) получена аналогично системе уравнений (1.1). Вероятности переходов для состояний системы совпадают с точностью до замены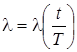 
.
Систему (2.1) будем решать в условиях перегрузки, то есть при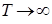 
.
Первое приближение
В системе уравнений (2.1) произведем замену переменных: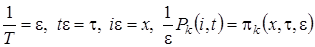 
. В результате такой замены производится переход от дискретной переменной 
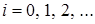к непрерывной переменной 
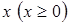, от t перешли к 
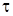, причем 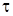такое, что 
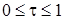. После замены производная равна 
.
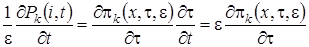Тогда уравнения (2.1) перепишем
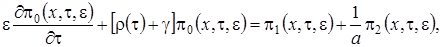
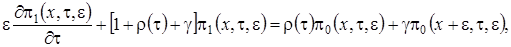(2.2)
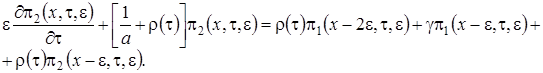
Решим систему уравнений (2.2) в два этапа.
1 этап. Считая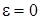 
и предполагая, что 
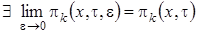будем иметь
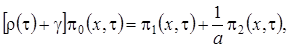
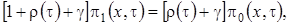(2.3)
.
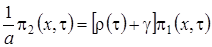Выразим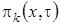 
через функцию 
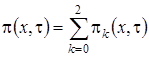и получим
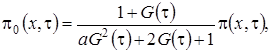
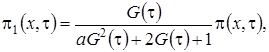(2.4)
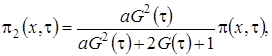
где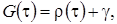 
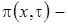асимптотическая плотность распределения нормированного числа заявок в источнике повторных вызовов.
Обозначим
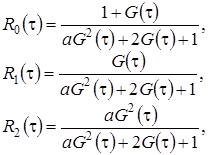(2.5)
( 
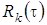- это асимптотическая вероятность того, что обслуживающий прибор находится в состоянии k). Заметим, что из системы (2.3) следуют равенства связывающие 
, 
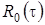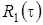и 
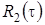
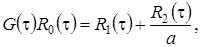
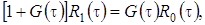(2.6)
.
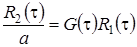Найдем вид функции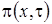 
, для этого перейдем ко второму этапу.
2 этап. В системе дифференциальных уравнений (2.2) все функции с аргументом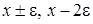 
разложим в ряд по приращению аргумента 
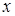, ограничиваясь слагаемыми порядка 
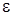, получим
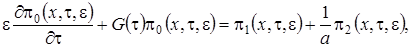
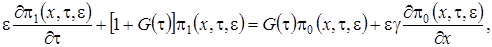(2.7)
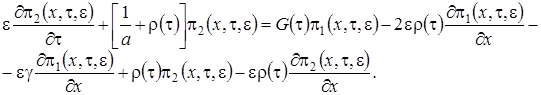
Просуммируем левые и правые части уравнений системы (2.7) и получим равенство
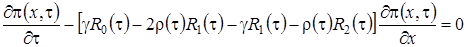. (2.8)
С учетом того, что
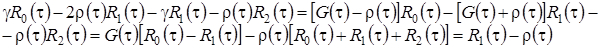
равенство (2.8) принимает вид
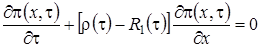. (2.9)
Уравнение (2.9) является однородным линейным уравнением с частными производными первого порядка. Для того чтобы его решить составим уравнение
,
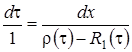его решение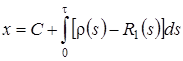 
, тогда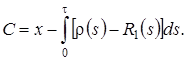 
Общее решение уравнения (2.9) имеет вид
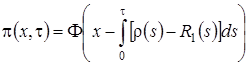, (2.10)
где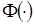 
- произвольная дифференцируемая функция, аналитическое выражение которой найдем из начальных условий.
Пусть распределение в начальный момент времени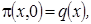 
где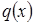 
некоторая плотность распределения. Тогда 
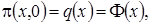следовательно 
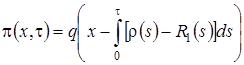. Возьмем в качестве начальной плотности распределения 
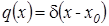, где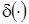 
- дельта-функция Дирака, а 
, 
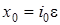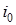- число заявок в источнике повторных вызовов в начальный момент времени.
Таким образом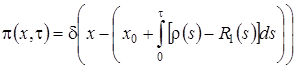 
, из свойств функции Дирака следует, что 
.
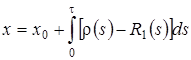То есть мы получили, что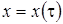 
, 
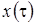имеет смысл асимптотического среднего.
Из приведенных рассуждений вытекает еще одно важное следствие, а именно
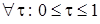имеет место 
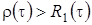, тогда 
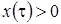(отрицательная функция 
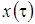противоречит смыслу задачи). В нашем случае 
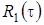совпадает с пропускной способностью системы.
Перейдем ко второму приближению, в котором будем искать распределение отклонения от асимптотического среднего.
Второе приближение
В исходной системе уравнений (2.1) сделаем замену переменных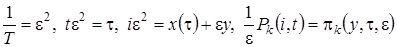 
.
Заметим, что в новых обозначениях производная по времени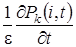 
равна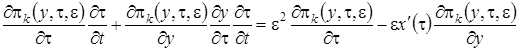 
. С учетом этого система (2.1) примет вид
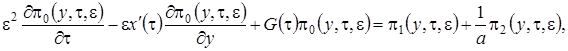
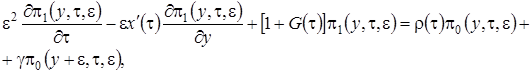(2.11)
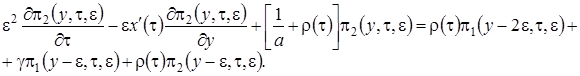
Решение системы уравнений (2.11) аналогично решению системы (2.2), но проводится в три этапа.
1 этап. В системе дифференциальных уравнений (2.13) сделаем предельный переход при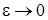 
и предположим, что 
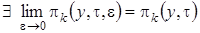, получим
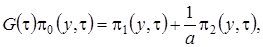
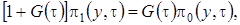(2.12)
.
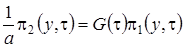Решим эту систему аналогично тому, как решили систему уравнений (2.3). Введем функцию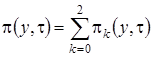 
и выразим через нее 
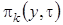, получим
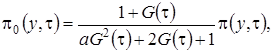
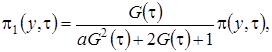(2.13)
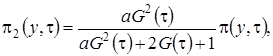
где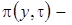 
асимптотическая плотность распределения отклонения числа заявок в источнике повторных вызовов от асимптотического среднего.
2 этап. Функции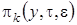 
будем искать с точностью до 
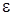в форме
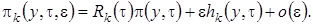(2.14)
Найдем вид функци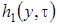й 
, 
и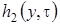 
. Для этого в системе дифференциальных уравнений (2.11) все функции с аргументом 
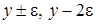разложим в ряд по приращению аргумента 
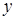, ограничимся слагаемыми порядка 
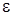. Получим
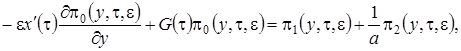
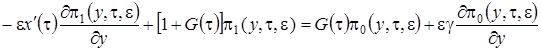(2.15)
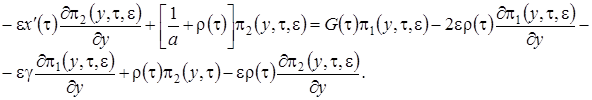
В уравнения (2.15) подставим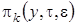 
в форме (2.14), приведем подобные и получим систему неоднородных линейных алгебраических уравнений относительно 
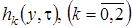вида
,
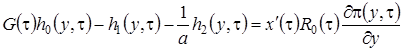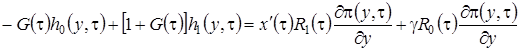, (2.16)
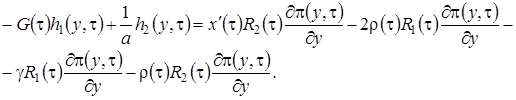
Нетрудно увидеть, что между уравнениями этой системы есть зависимость и ранг матрицы системы равен, следовательно, чтобы решение уравнений (2.16)существовало, необходимо выполнение равенства
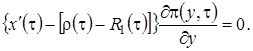(2.17)
Из однородного линейного уравнения с частными производными первого порядка (2.9) мы знаем, что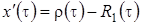 
. Таким образом, можно сделать вывод, что система (2.16) разрешима. При условии, что функция 
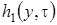известна, решение можно записать в виде
,
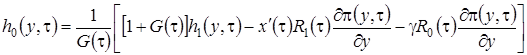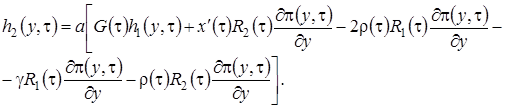(2.18)
Теперь все готово, для того, чтобы найти функцию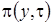 
. Перейдем к третьему этапу.
3 этап. В системе дифференциальных уравнений (2.11) все функции с аргументом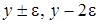 
разложим в ряд по приращению аргумента 
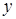, ограничиваясь слагаемыми порядка 
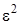, получим
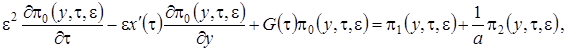
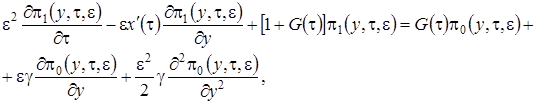(2.19)
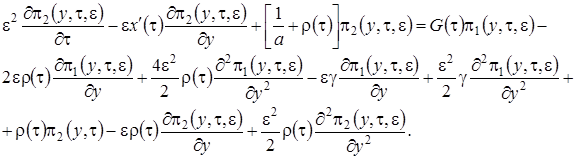
Теперь подставим в уравнения (2.19) 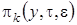в форме (2.14) и просуммируем левые и правые части уравнений, будем иметь
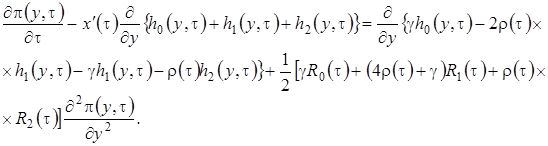(2.20)
Подставляя вместо и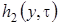 
их выражения, полученные на втором этапе получим для 
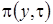уравнение Фоккера-Планка
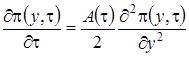, (2.21)
где
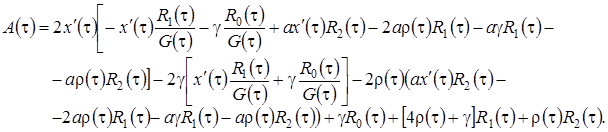
Нормированным решением полученного одномерного уравнения диффузии [8] является плотность нормального распределения вероятностей с нулевым средним и дисперсией
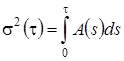. (2.22)
Дата: 2019-07-24, просмотров: 260.
