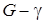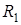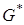Рассмотрим спутниковую сеть связи, управляемую динамическим протоколом случайного множественного доступа с оповещением о конфликте. Архитектура такой сети состоит из большого числа территориально-распределенных абонентских станций (АС), которые передают сообщения через геостационарный спутник-ретранслятор. Так как спутниковый канал связи совместно используют все АС, то возможно совпадение времени ретрансляции сообщений от двух или более АС, при этом сообщения искажаются и требуют повторной передачи. Такая ситуация называется конфликтом. Предполагается, что спутник-ретранслятор имеет возможность обнаружения возникающих конфликтов и реализации сигнала оповещения. Абонентские станции способны воспринимать (идентифицировать) сигнал оповещения о конфликте, так, чтобы в каждой АС по прошествии заданного времени распространения сигнала можно было определить, правильно приняты переданные сообщения или нет.
Сообщения, поступающие на спутник-ретранслятор во время распространения сигнала оповещения о конфликте, считаются искаженными. Все искаженные сообщения поступают в источник повторных вызовов (ИПВ). После определения АС того, что посланное сообщение попало в конфликт, АС производит случайную задержку, после которой вновь реализует передачу. В динамическом протоколе предлагается использовать случайную задержку повторной попытки, распределенную экспоненциально с параметром, зависящим от количества сообщений, находящихся в ИПВ. Динамические протоколы, как правило, не реализуемы. Но могут приближенно оценивать функционирование адаптивных протоколов, в которых количество заявок в ИПВ заменяется некоторым оценочным числом.
В качестве математической модели сети связи, управляемой динамическим протоколом случайного множественного доступа с оповещением о конфликте, рассмотрим однолинейную СМО. Прибор (спутник-ретранслятор) может находиться в одном из трех состояний:
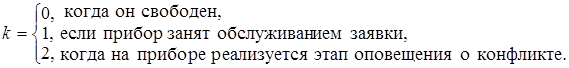
Каждая заявка в момент поступления в систему встает на прибор и немедленно начинает обслуживаться. Если за время ее обслуживания другие заявки не поступали, то она после окончания обслуживания покидает систему и в дальнейшем не рассматривается. Если же за время ее обслуживания поступает другая заявка, то возникает конфликтная ситуация и начинается этап оповещения о конфликте, длительность которого распределена по экспоненциальному закону.
Заявки, попавшие в конфликт, а также поступающие в систему во время оповещения о конфликте, автоматически переходят в источник повторных вызовов (ИПВ). Из него они вновь обращаются к прибору с попыткой повторного обслуживания через случайные интервалы времени, распределенные по экспоненциальному закону с параметром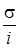 
(i – число заявок в ИПВ в момент времени t), и могут вновь попасть в конфликтные передачи. После успешной передачи заявка покидает систему.
Время обслуживания распределено по одному и тому же показательному закону с параметром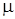 
, как для первичных, так и для повторных вызовов.
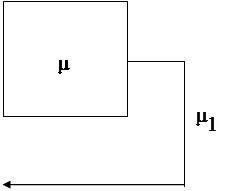
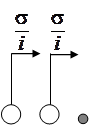
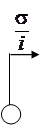
Будем считать, что на вход системы поступает простейший поток заявок с параметром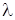 
. Структура такой СМО имеет вид рис. 1.1.
Состояние рассматриваемой системы определим вектором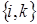 
, изменение во времени которого образует однородный дискретный двумерный марковский процесс 
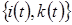с бесконечным числом состояний.
 |  | |||||||||||
 |  | |||||||||||
 |  | |||||||||||
 | ||||||||||||
Рис. 1.1 – Модель системы массового обслуживания
Математическая модель исследуемого протокола множественного доступа построена, проведем ее анализ, получим аналитические выражения, определяющие зависимости для основных ее характеристик.
Для исследования процесса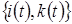 
введем следующие обозначения
,
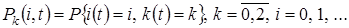вероятность того, что в момент времени t прибор находится в состоянии k и в ИПВ находится i заявок.
Рассмотрим вероятности переходов из состояния системы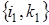 
в произвольный момент времени t в состояние 
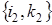за бесконечно малый интервал времени 
.
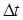1. Пусть система находится в состоянии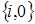 
, то есть в ИПВ находится i заявок и прибор свободен, за интервал времени 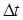состояние системы может измениться таким образом (рис. 1.2):
а) с вероятностью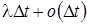 
из входящего потока требований поступит новая заявка, которая немедленно займет прибор и начнет обслуживание, тогда система в момент времени 
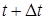будет находиться в состоянии 
;
б) с вероятностью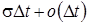 
к прибору обратится одна из i заявок, находящихся в ИПВ и система перейдет в состояние 
;
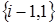в) с вероятностью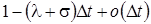 
состояние системы не изменится.
2. Пусть система в момент времени t находится в состоянии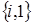 
, то есть прибор занят обслуживанием заявки и в ИПВ находится i требований, за интервал времени 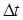возможны следующие переходы (рис. 1.3):
а) с вероятностью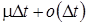 
прибор успешно завершит обслуживание, и в момент времени 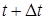система будет находиться в состоянии ;
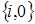б) с вероятностью 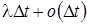в систему поступит новое требование из входящего потока и произойдет конфликт. Как вновь поступившая, так и заявка с прибора перейдут в ИПВ, и начнется интервал оповещения о конфликте, следовательно, система перейдет в состояние 
;
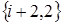в) с вероятностью 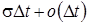к прибору обратится одна из заявок с ИПВ, произойдет конфликт, и обе заявки переместятся в ИПВ, следовательно, система в момент времени 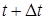будет находиться в состоянии 
;
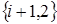г) с вероятностью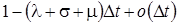 
состояние системы не изменится.
3. Пусть система в момент времени t находится в состоянии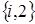 
. Посмотрим, что произойдет через интервал времени длины 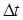(рис. 1.4):
а) с вероятностью 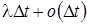к прибору обратится заявка из входящего потока, которая автоматически попадет в ИПВ. В момент времени 
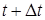система будет в состоянии ;
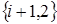б) с вероятностью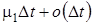 
интервал оповещения о конфликте завершится, и система перейдет в состояние ;
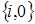в) с вероятностью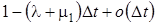 
состояние системы не изменится.
Все остальные вероятности переходов не превышают порядка малости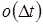 
.
 |
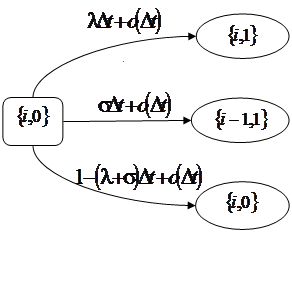Рис. 1.2 – Возможные переходы из состояния 
 |
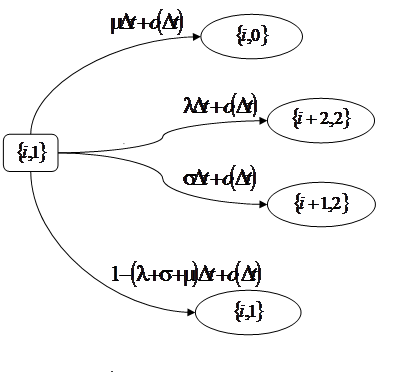Рис. 1.3 – Возможные переходы из состояния 
 |
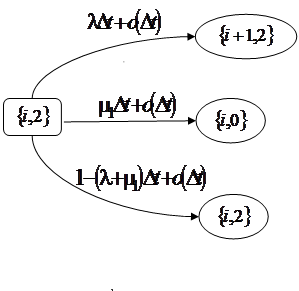Рис. 1.4 – Возможные переходы из состояния 
Таким образом, можно записать систему конечно-разностных уравнений для вероятностей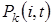 
состояний системы:
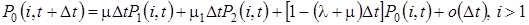
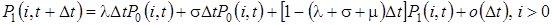
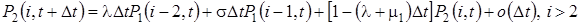
следовательно, в нестационарном режиме, эти вероятности удовлетворяют системе дифференциально-разностных уравнений
,
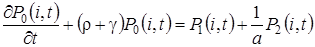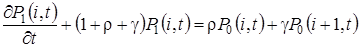, (1.1)
,
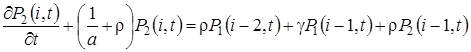где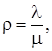 
,
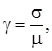
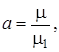
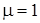решить которую практически невозможно, но можно решить асимптотически в условиях «большой загрузки», т.е. при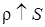 
, 
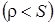, где 
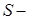пропускная способность исследуемой сети связи (верхняя граница множества тех значений загрузки 
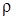, для которых в системе существует стационарный режим).
Рассмотрим исходную систему уравнений (1.1) и произведем в ней замену переменных: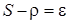 
, 
, 
, 
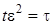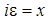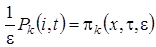. В результате замены производится переход от дискретной переменной 
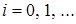к непрерывной переменной 
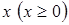. В новых обозначениях производная равна 
.
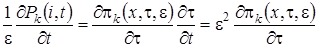Тогда систему (1.1) перепишем
,
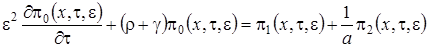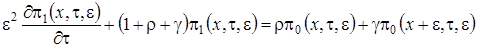, (1.2)
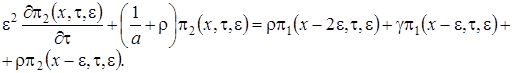
Получим вид решения системы (1.2), которую будем решать в три этапа.
1 этап. В уравнениях (1.2) устремим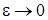 
и обозначим 
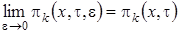, заметим что, 
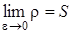. Будем иметь
,
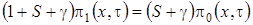, (1.3)
.
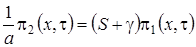Выразим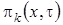 
через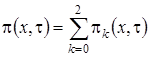 
и получим
,
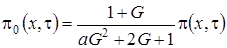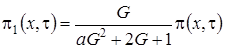, (1.4)
.
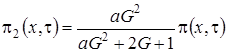где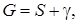 
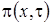– асимптотическая плотность распределения вероятностей нормированного числа заявок в ИПВ.
Введем обозначения
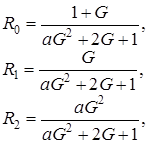(1.5)
( 
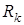- это асимптотическая вероятность того, что обслуживающий прибор находится в состоянии k). Из системы (1.3) следуют равенства, связывающие 
, 
, 
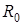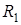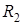и выглядят так
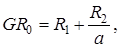
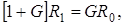(1.6)
.
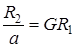Найдем вид функции 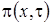. Для этого перейдем ко второму этапу.
2 этап. Неизвестные функции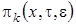 
будем искать с точностью до 
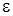в следующем виде
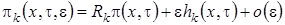, (1.7)
Определим вид функций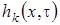 
, для этого в системе уравнений (1.2) разложим функции с аргументом 
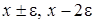в ряд по приращению аргумента 
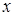(ограничиваясь двумя слагаемыми), будем иметь
,
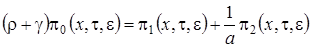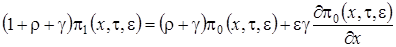, (1.8)
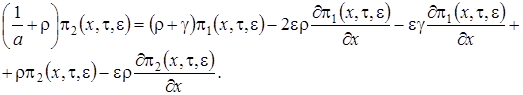
В полученные уравнения подставим 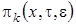в форме (1.7), заменим 
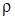разностью 
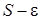, сумму 
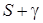на G и не учтем слагаемые, имеющие порядок 
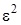. Получим
,
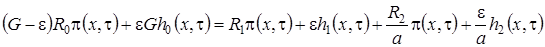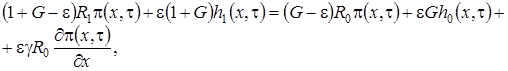(1.9)
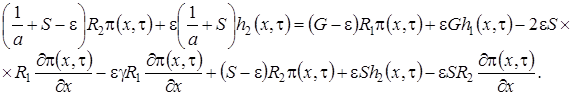
Теперь приведем подобные слагаемые, учтем равенства (1.6), и получим неоднородную линейную систему алгебраических уравнений для нахождения неизвестных функций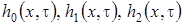 
такого вида
,
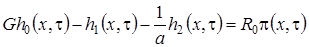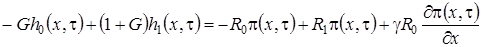, (1.10)
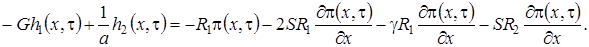
Нетрудно заметить, что ранг матрицы однородной системы алгебраических уравнений, соответствующей (1.10) равен двум. Следовательно, для того, чтобы система была разрешима, необходимо, чтобы ранг расширенной матрицы этой системы был равен двум, т.е. чтобы выполнялось следующее равенство
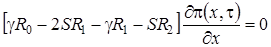. (1.11)
С учетом того, что
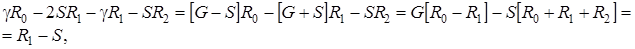равенство (1.11) принимает вид
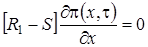. (1.12)
Равенство нулю производной противоречит смыслу задачи, следовательно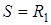 
, т. е. пропускная способность исследуемой сети связи равна асимптотической вероятности того, что обслуживающий прибор «обслуживает», на рис. 1.5 продемонстрирован этот результат.
|
|
|
|
|
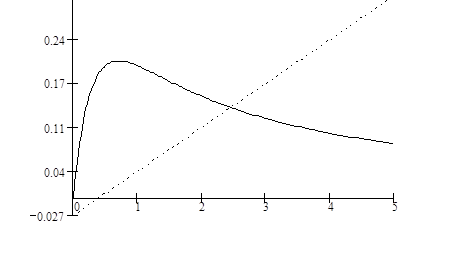
Рис. 1.5
Таким образом, мы выяснили, что система (1.10) разрешима. Ее решение можно записать так
,
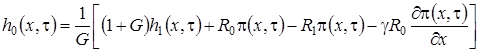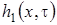- произвольная функция, (1.13)
.
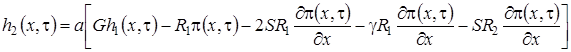Перейдем к третьему этапу.
3 этап. Запишем уравнения системы (1.2) с точностью до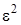 
, получим
,
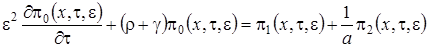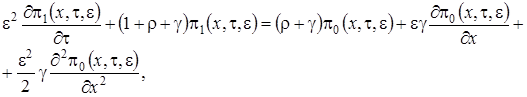(1.14)
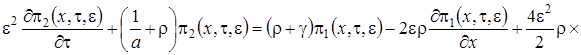
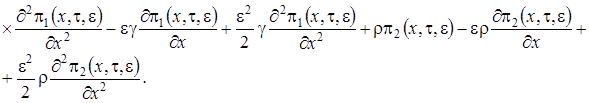
Как и на втором этапе в полученные уравнения подставим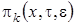 
в форме (1.7), заменим 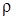разностью 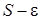, сумму 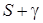на G и не учтем слагаемые, имеющие порядок выше 
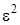, получим
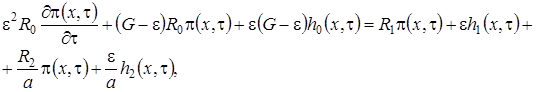
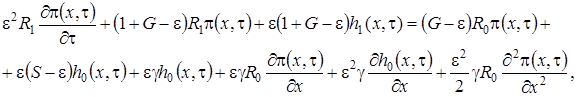(1.15)
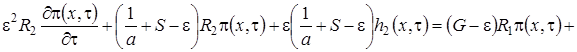
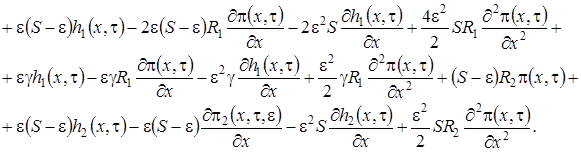
Просуммировав все уравнения системы (1.15), получим равенство для нахождения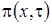 
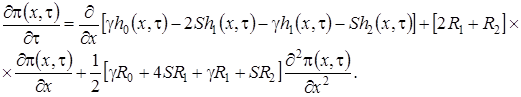(1.16)
Подставляя выражения для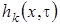 
, найденные на втором этапе, для 
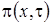получим уравнение Фоккера-Планка
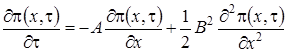, (1.17)
где
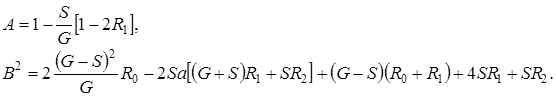
Решим уравнение (1.17) с помощью преобразования Лапласа по x. Левую и правую части уравнения умножим на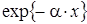 
и проинтегрируем. С учетом обозначения 
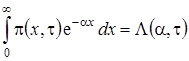и свойств этой функции уравнение (1.17) приобретет вид
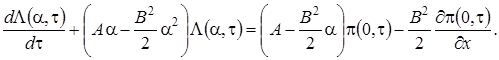(1.18)
Таким образом, мы перешли от уравнения Фоккера-Планка с постоянными коэффициентами к обыкновенному дифференциальному уравнению, решение которого с точностью до неизвестных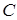 
, 
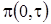и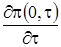 
записывается следующим образом
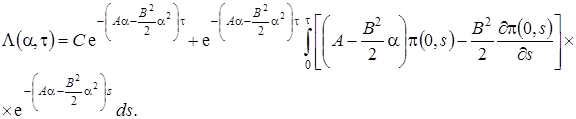(1.19)
Для того чтобы получить окончательное решение уравнения (1.17) нужно провести дополнительное исследование, которое бы показало поведение исследуемого процесса в окрестности нуля. Используя асимптотику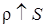 
, это не удается сделать.
Предположим, что сеть связи функционирует в стационарном режиме, тогда (1.17) перепишется в виде
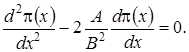(1.20)
Следовательно, в стационарном режиме асимптотическое распределение вероятностей нормированного числа заявок в источнике повторных вызовов подчиняется экспоненциальному закону с параметром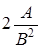 
и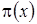 
имеет вид
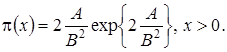(1.21)
Дата: 2019-07-24, просмотров: 273.
