Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Техническое зрение роботов

ВВЕДЕНИЕ

С целью классификации методов и подходов, используемых в си­стемах технического зрения, зрение разбито на три ос­новных подкласса: зрение низкого, среднего и высокого уров­ней. Системы технического зрения низкого уровня предназначены для обработки информа­ции с датчиков очувствления.

Эти системы можно отнести к классу «интеллектуальных» машин, если они обладают следующими признаками (призна­ками интеллектуального поведения):

1) возможностью выделения существенной информации из множества независимых признаков;

2) способностью к обучению на примерах и обобщению этих знаний с целью их применения в новых ситуациях;

3) возможностью восстановления событий по неполной ин­формации;

4) способностью определять цели и формулировать планы для достижения этих целей.

Создание систем технического зрения с такими свойствами для ограниченных видов рабочего пространства в принципе воз­можно, но характеристики таких систем далеки от возможностей человеческого зрения. В основе технического зрения лежит аналитическая формализация, направленная на решение конкрет­ных задач. Машины с сенсорными характеристиками, близкими к возможностям человека, по-видимому, появятся еще не скоро. Однако отметим, что копирование природы не является единст­венным решением этой проблемы. Читателю наверняка известны ранние экспериментальные образцы аэропланов с машущими крыльями и другими особенностями полета птиц. Современное решение задачи о полете в пространстве в корне отличается от решений, подсказанных природой. По скорости и достижимой высоте самолеты намного превосходят возможности птиц.

Системы технического зрения среднего уровня связаны с задачами сегментации, описания и распознавания отдельных объектов. Эти задачи охватывают множество подходов, ос­нованных на аналитических представлениях. Системы техниче­ского зрения высокого уровня решают проблемы, рассмотренные выше. Для более ясного понимания проблем технического зре­ния высокого уровня и его связи с техническим зрением низкого и среднего уровней введем ряд ограничений и упростим решае­мую задачу.

 

СЕГМЕНТАЦИЯ

Сегментацией называется процесс подразделения сцены на составляющие части или объекты. Сегментация является одним из основных элементов работы автоматизированной системы технического зрения, так как именно на этой стадии обработки объекты выделяются из сцены для дальнейшего распознавания и анализа. Алгоритмы сегментации, как правило, основываются на двух фундаментальных принципах: разрывности и подобии. В первом случае основной подход основывается на определении контуров, а во втором — на определении порогового уровня и расширении области. Эти понятия применимы как к статиче­ским, так и к динамическим (зависящим от времени) сценам. В последнем случае движение может служить мощным средст­вом для улучшения работы алгоритмов сегментации.

Проведение контуров и определение границы

Методы - вычисление градиента, пороговое разделение - определяют разрывы в интенсивности представления образа объекта. В идеальном слу­чае эти методы определяют пикселы, лежащие на границе меж­ду объектом и фоном. На практике данный ряд пикселов редко полностью характеризует границу из-за шума, разрывов на гра­нице вследствие неравномерной освещенности и других эффек­тов, приводящих к размытию изображения. Таким образом, ал­горитмы обнаружения контуров сопровождаются процедурами построения границ объектов из соответствующих последователь­ностей пикселов. Ниже рассмотрено несколько методик, при­годных для этой цели.

Локальный анализ.

Одним из наиболее простых подходов соединения точек контура является анализ характеристик пик­селов в небольшой окрестности (например, в окрестности раз­мером 3 X 3 или 5 X 5) каждой точки (х, у) образа, который уже подвергся процедуре обнаружения контура. Все точки, яв­ляющиеся подобными (определение критерия подобия дано ниже), соединяются, образуя границу из пикселов, обладающих некоторыми общими свойствами.

При таком анализе для установления подобия пикселов кон­тура необходимо определить:

1 )    величину градиента, требуемого для построения контурного пиксела,

 2) направление градиен­та.

Первая характеристика обозначается величиной G{f(x, у)] .

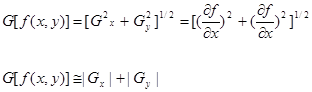
Таким образом, пиксел контура с координатами (х', у') подобен по величине в определенной ранее окрестности (х, у) пикселу с координатами (х, у), если справедливо неравенство

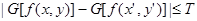
где Т —пороговое значение.

Направление градиента устанавливается по углу вектора градиента, определенного в уравнении

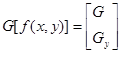
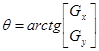
где q—угол (относительно оси х), вдоль которого скорость изменения имеет наибольшее значение. Тогда можно сказать, что угол пиксела контура с координатами { х', у') в некоторой окрестности (х, у) подобен углу пиксела с координатами { х, у) при выполнении следующего неравенства:

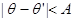
где А—пороговое значение угла. Необходимо отметить, что на­правление контура в точке { х, у) в действительности перпенди­кулярно направлению вектора градиента в этой точке. Однако для сравнения направлений неравенство  дает эквивалент­ные результаты.

Основываясь на этих предположениях, мы соединяем точку в некоторой окрестности (х, у) с пикселом, имеющим коорди­наты (х, у), если удовлетворяются критерии по величине и направлению. Двигаясь от пиксела к пикселу и представляя каждую присоединяемую точку как центр окрестности, процесс повторяется для каждой точки образа. Для установления соот­ветствия между уровнями интенсивности освещения и последо­вательностями пикселов контура применяется стандартная биб­лиотечная процедура.

Цель состоит в определении размеров прямоугольни­ков, с помощью которых можно построить качественное изобра­жение. Построение таких прямоугольников осуществляется в ре­зультате определения строго горизонтальных и вертикальных контуров. Дальнейший процесс состоял в соединении сегментов контура, разделенных небольшими промежутками, и в объединении отдельных корот­ких сегментов.

2.1.2.Глобальный анализ с помощью преобразования Хоуга.

Рас­смотрим метод соединения граничных точек путем определения их расположения на кривой специального вида. Первоначально предполагая, что на плоскости ху образа дано п точек, требуется найти подпоследовательности точек, лежащих на прямых линиях. Одно из возможных решений состоит в построении всех линий, проходящих через каждую пару точек, а затем в нахож­дении всех подпоследовательностей точек, близких к определен­ным линиям. Задача, связанная с этой процедурой, заключается в нахождении п(п— 1)/2 ~ п² линий и затем в осуществлении п [п(п—1)]/2 ~ п ³ сравнений каждой точки со всеми линиями. Этот процесс трудоемок с вычислительной точки зрения за ис­ключением самых простых приложений.

Данную задачу можно решить по-другому, применяя подход, предложенный Хоугом и называемый преобразованием Хоуга. Рассмотрим точку (х_i y_i) и общее уравнение прямой ли­нии у:= аx _i + b_i. Имеется бесконечное число линий, проходящих через точку (х_i y_i), но все они удовлетворяют уравнению у:= аx _i + b_i при различных значениях а и b. Однако, если мы за­пишем это уравнение в виде b = -х_i а + y_i и рассмотрим пло­скость а b (пространство параметров), тогда мы имеем уравне­ние одной линии для фиксированной пары чисел (х_i y_i). Более того, вторая точка (х _j, у _j) также имеет в пространстве пара­метров связанную с ней линию, которая пересекает другую ли­нию, связанную с точкой (х_i y_i) в точке (а', b’), где значения а' и b’—параметры линии, на которой расположены точки (х_i y_i) и (х_j, у _j) в плоскости ху. Фактически все точки, расположен­ные на этой линии, в пространстве параметров будут иметь ли­нии пересечения в точке (а', b’).

Вычислительная привлекательность преобразования Хоуга заключается в разделении пространства параметров на так на­зываемые собирающие элементы , где (a_макс, а_мин) и (b_макс, b_мин)—допустимые величины параметров линий. Собирающий элемент A (i, j) соответствует площади, связанной с ко­ординатами пространства параметров (а_i, b_j). Вначале эти элементы считаются равными нулю. Тогда для каждой точки (x_k, у _k) в плоскости образа мы полагаем параметр а равным каж­дому из допустимых значений на оси а и вычисляем соответст­вующее b, используя уравнение b = -х _k + y _k Полученное значение b затем округляется до ближайшего допустимого зна­чения на оси b. Если выбор a_р приводит к вычислению b_q, мы полагаем А(р, q) ==А(р, q) + 1. После завершения этой про­цедуры значение М в элементе A (i, j) соответствует М точкам в плоскости xy, лежащим на линии y= a_ix+b. Точность рас­положения этих точек на одной прямой зависит от числа раз­биений плоскости аb. Отметим, что, если мы разбиваем ось а на К частей, тогда для каждой точ­ки (x_k, у _k) мы получаем К зна­чений b, соответствующих К воз­можным значениям а. Посколь­ку имеется п точек образа, про­цесс состоит из пК вычислитель­ных операций. Поэтому приве­денная выше процедура линейна относительно п и имеет меньшее число вычислительных опера­ций, чем процедура, описанная выше, если К<= п.

Проблема, связанная с пред­ставлением прямой линии урав­нением у = ах + b, состоит в том, что оба параметра а и b стремятся к бесконечности, если линия принимает вертикаль­ное положение. Для устранения этой трудности используется нормальное представление прямой линии в виде

xcos q +ysin q = b .        

Это представление для построения таблицы собирающих элементов используется так же, как метод, изложенный выше, но вместо прямых линий мы имеем синусоидальные кривые в плоскости q r. Как и прежде, М точек, лежащих на прямой xcos q _i+уsinq_i == r _i , соответствуют М синусоидальным кривым, кото­рые пересекаются в точке (q _i, r _i) пространства параметров. Если используется метод возрастания q и нахождения для него соот­ветствующего r, процедура дает М точек в собирающий элемент А (i, j), связанный с точкой (q _i, r _i).

Применение движения

Движение представляет собой мощное средство, которое ис­пользуется человеком и животными для выделения интересую­щих их объектов из фона. В системах технического зрения ро­ботов движение используется при выполнении различных операций на конвейере, при перемещении руки, оснащенной дат­чиком, более редко при перемещении всей робототехнической системы.

Основной подход.

Один из наиболее простых подходов для определения изменений между двумя кадрами изображения (образами) f(x, у, ti) и f(x, у, t,), взятыми соответственно в моменты времени ti и t j, основывается на сравнении соответ­ствующих пикселов этих двух образов. Для этого применяется процедура, заключающаяся в формировании так называемой разности образов.

Предположим, что мы имеем эталонный образ, имеющий только стационарные компоненты. Если сравним этот образ с таким же образом, имеющим движущиеся объекты, то разность двух образов получается в результате вычеркивания стацио­нарных компонент (т. е. оставляются только ненулевые записи, которые соответствуют нестационарным компонентам изобра­жения).

Разность между двумя кадрами изображения, взятыми в мо­менты времени ti и tj, можно определить следующим образом:

 

dij(x,y) = (*)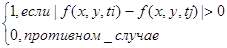

 

где q—значение порогового уровня. Отметим, что dij(x, у) при­нимает значение 1 для пространственных координат (х, у) только в том случае, если два образа в точке с этими координа­тами существенно различаются по интенсивности, что опреде­ляется значением порогового уровня q.

При анализе движущегося образа все пикселы изображений разности dij(x, у), имеющие значение 1, рассматриваются как результат движения объекта. Этот подход приметим только в том случае, если два образа зарегистрированы и освещен­ность имеет относительно постоянную величину в пределах границ, устанавливаемых пороговым уровнем q. На практике записи в dij(x, у), имеющие значение 1, часто появляются в ре­зультате действия шума. Обычно на разности двух кадров изо­бражения такие значения выглядят как изолированные точки. Для их устранения применяется простой подход, заключающийся в формировании 4- или 8-связных областей из единиц в dij(x, у), и затем пренебрегают любой областью с числом записей, мень­шим заранее заданного. При этом можно не распознать малые и/или медленно движущиеся объекты, но это увеличивает ве­роятность того, что остающиеся записи в разности двух кадров изображения действительно соответствуют движению.

Аккумулятивная разность.

Как говорилось выше, разность кадров благодаря шуму часто содержит изолированные записи. Несмотря на то что число таких записей может быть сокращено или полностью ликвидировано в результате анализа связности пороговых уровней, этот процесс может также привести к по­тере изображений малых или медленно движущихся объектов. Ниже излагается подход для решения этой проблемы путем рассмотрения изменения в расположении пикселов на несколь­ких кадрах, т. е. в процесс вводится «память». Основная идея заключается в пренебрежении теми изменениями, которые воз­никают случайно в последовательности кадров и, таким образом, могут быть отнесены к случайному шуму.

Рассмотрим последовательность кадров изображения f (x,y,t1), f(x, у, t2), ..., f(x, у, tn) и допустим, что f(x, у, t1) является эталонным образом. Изображение аккумулятивной разности формируется в результате сравнения эталонного об­раза с каждым образом в данной последовательности. В процедуре построения изображения аккумулятивной разности имеется счетчик, предназначенный для учета расположения пик­селов. Его значение увеличивается каждый раз, когда возникает различие в расположении соответствующих пикселов эталон­ного образа и образа из рассматриваемой последовательности. Таким образом, когда k- й кадр сравнивается с эталонным, запись в данном пикселе аккумулятивней разности означает, во сколько раз интенсивность пиксела k-го кадра отличается от ин­тенсивности пиксела эталонного образа. Различия устанавли­ваются, например, с помощью уравнения (*).

Приведенные выше рассуждения иллюстрируются рисунке. На рисунке а—д приведены образы прямоугольного объекта (обозначенного нулями), движущегося вправо с постоянной ско­ростью 1 пиксел/кадр. Эти образы приведены в моменты вре­мени, соответствующие одному перемещению пиксела. На рис. (а) изображен кадр эталонного образа, на рис. (г) со 2-го по 4-й кадры последовательности, а на рис. (д)— 11-й кадр. Рис. (е— и) соответствуют изображениям аккумулятив­ной разности, которые можно объяснить следующим образом. На рис. (е) левая колонка из 1 обусловлена различием между объектом на рис. (а), и фоном на рис. (б). Правая колонка из 1 вызвана различием между фоном эталонного образа и пе­редним контуром движущегося объекта. Ко времени появления 4-го кадра (рис. г), первый ненулевой столбец изображе­ния аккумулятивной разности указывает на три отсчета, что со­ответствует трем основным различиям между этим столбцом в эталонном образе и соответствующим столбцом в последующих кадрах. На рис. и показано общее число из 10 (представ­ленных «A» в шестнадцатеричной системе счисления) изменений этого положения. Остальные записи на этом рисунке объясня­ются аналогично.

Нередко полезно рассматривать три типа изображений акку­мулятивной разности: абсолютное, положительное и отрица­тельное. Последние два получаются из уравнения (*), в котором нет модуля, а вместо f(x, у, ti) подставляется значение эталонного кадра. Предполагая, что числовые значения интен­сивности объекта превышают значения фона в случае, когда разность положительна, она сравнивается с положительным значением порогового уровня; если отрицательна, сравнение выполняется с отрицательным значением порогового уровня. Это определение заменяется на противоположное, если интенсив­ность объекта меньше фона.

Рис. Кадр эталонного образа (а), б—д соответственно 2-, 3-, 4- и 11-й кадры, е—и—изображения аккумулятивной разности для 2-, 3-, 4- и 11-го кадров .

	9
	10	00000000
	11	00000000
	12	00000000
a	13	00000000
	14	00000000
	15	00000000
	16
	9		9
	10	00000000	10	1	1
	11	00000000	11	1	1
	12	00000000	12	1	1	е
б	13	00000000	13	1	1
	14	00000000	14	1	1
	15	00000000	15	1	1
	16		16
	9		9
	10	00000000	10	21	21
	11	0000000C	11	21	21
в	12	0000000C	12	21	21	ж
	13	0000000C	13	21	21
	14	00000000	14	21	21
	15	00000000	15	21	21
	16		16
	9		9
	10	00000000	10	321	321
	11	00000000	11	321	321
г	12	00000000	12	321	321	з
	13	00000000	13	321	321
	14	00000000	14	321	321
	15	00000000	15	321	321
	16		16
	9		9
	10	00000000	10	A9876	5438887654321
	11	00000000	11	A9876	5438887654321
	12	00000000	12	A9876	5438887654321
д	13	00000000	13	A9876	5438887654321	и
	14	00000000	14	A9876	5438887654321
	15	00000000	15	A9876	543888.7654321
	16		16

 

ОПИСАНИЕ

В системах технического зрения проблемой описания назы­вается выделение свойств (деталей) объекта с целью распозна­вания. В идеальном случае дескрипторы не должны зависеть от размеров, расположения и ориентации объекта, но должны содержать достаточное количество информации для надежной идентификации объектов. Описание является основным резуль­татом при конструировании систем технического зрения в том смысле, что дескрипторы должны влиять не только на слож­ность алгоритмов распознавания, но также и на их работу. рассмотрим три основные катего­рии дескрипторов: дескрипторы границы, дескрипторы области и дескрипторы для описания трехмерных структур.

Дескрипторы границы.

Цепные коды.

Цепные коды применяются для представления границы в виде последовательности отрезков прямых линий определенной длины и направления. Обычно в основе этого представления лежит 4- или 8-связная прямоугольная решетка. Длина каждого отрезка определяется разрешением решетки, а направления задаются выбранным кодом. Отметим что для представления всех направлений в 4-направленном цеп­ном коде достаточно 2 бит, а для 8-направленного цепного кода требуется 3 бит. Для порождения цепного кода заданной границы сначала выбирается решетка. Тогда, если площадь ячейки, расположенной внутри границы, больше определенного числа (обычно 50%), ей присваивается значение 1; в противном слу­чае этой ячейке присваивается значение 0. Окон­чательно мы кодируем грани­цу между двумя областями, используя направления. Результат кодирования в на­правлении по часовой стрелке с началом в месте, помеченном точкой. Альтернативная процедура состоит в разбиении границы на участки равной длины (каждый участок имеет одно и то же число пикселов) и соединении граничных точек

каждого участка прямой линией, а затем присваивания каждой линии направления, ближайшего к одному из допустимых направлений цепного кода. Важно отметить, что цепной код данной границы зависит от начальной точки. Однако можно нормировать код с помощью простой процедуры. Для создания цепного кода начальная точка на решетке выбирается произвольным образом. Рассмат­ривая цепной код как замкнутую последовательность индексов направлений, мы вновь выбираем начальную точку таким обра­зом, чтобы результирующая последовательность индексов была целым числом, имеющим минимальную величину. Также можно нормировать повороты, если вместо цепного кода рассматри­вать его первую разность. Первая разность вычисляется в ре­зультате отсчитывания (в направлении против часовой стрелки)' числа направлений, разделяющих два соседних элемента кода. Например, первая разность для цепного кода с 4 направле­ниями 10103322 есть 3133030. Если рассматривать код как зам­кнутую последовательность, тогда первый элемент разности можно вычислить, используя переход между последним и пер­вым компонентами цепи. В данном примере результатом яв­ляется 33133030. Нормирование можно осуществить путем раз­биения всех границ объекта на одинаковое число равных сег­ментов и последующей подгонкой длин сегментов кода с целью их соответствия этому разбиению.

Изложенные методы нормирования являются точными толь­ко в том случае, когда сами границы инвариантны к повороту и изменению масштаба. Этот случай редко встречается на прак­тике. Например, один и тот же объект, разбитый на элементы в двух различных направлениях, как правило, имеет разную форму границы, причем степень различия пропорциональна раз­решающей способности изображения. Этот эффект можно умень­шить, если выбирать длины элементов цепи большими, чем рас­стояния между пикселами дискретного образа, или же выбирать ориентацию решетки вдоль главных осей кодируе­мого объекта.

Сигнатуры.

Сигнатурой называется одномерное функциональ­ное представление границы. Известно несколько способов соз­дания сигнатур. Одним из наиболее простых является построе­ние отрезка из центра к границе как функции угла. Очевидно, что такие сигнатуры зависят от периметра области и начальной точки. Нормирование периметра можно осуществить, пронормировав кривую r(q) максимальным значением. Пробле­му выбора начальной точки можно решить, определив сначала цепной код границы, а затем применив метод, изложенный в пре­дыдущем разделе. Конечно, расстояние, зависящее от угла, не является единственным способом определения сигнатуры. Напри­мер, можно провести через границу прямую линию и определить угол между касательной к границе и этой линией как функцию положения вдоль границы. Полученная сигнатура, хотя и от­личается от кривой r(q), несет информацию об основных харак­теристиках формы границы. Например, горизонтальные участки кривой соответствовали бы прямым линиям вдоль границы, по­скольку угол касательной здесь постоянен. Один из вариантов этого метода в качестве сигнатуры использует так называемую функцию плотности наклона. Эта функция представляет со­бой гистограмму значений угла касательной. Поскольку гисто­грамма является мерой концентрации величин, функция плотно­сти наклона строго соответствует участкам границы с постоян­ными углами касательной (прямые или почти прямые участки и имеет глубокие провалы для участков, соответствующих быст­рому изменению углов (выступы или другие виды изгибов).

Дескрипторы области

Область, представляющую интерес, можно описать формой ее границы или же путем задания ее характери­стик. Важно отметить, что методы, рассмот­ренные выше, применяются для описания областей.

Текстура.

Во многих случаях идентификацию объектов или областей образа можно осуществить, используя дескрипторы текстуры. Хотя не существует формального определения тек­стуры, интуитивно этот дескриптор можно рассматривать как описание свойств поверхности (однородность, шероховатость, ре­гулярность). Двумя основными подходами для описания текстуры являются стати­стический и структурный. Статистические методы дают такие характеристики текстуры, как однородность, шероховатость, зер­нистость и т. д. Структурные методы устанавливают взаимное расположение элементарных частей образа, как, например, опи­сание текстуры, основанной на регулярном расположении па­раллельных линий.

Скелет области.

Важным подходом для описания вида струк­туры плоской области является ее представление в виде графа. Во многих случаях для этого определяется схема (скелет) об­ласти с помощью так называемых прореживающих (или же сокращающих) алгоритмов. Прореживающие процедуры иг­рают основную роль в широком диапазоне задач компьютерного зрения — от автоматической проверки печатных плат до под­счета асбестовых волокон в воздушных фильтрах. Скелет об­ласти можно определить через преобразование средних осей (ПСО), предложенное в работе. ПСО области R с грани­цей В определяется следующим образом. Для каждой точки р из R мы определяем ближайшую к ней точку, лежащую на В. Если р имеет больше одной такой точки, тогда о ней говорится, что она располагается на средней оси (скелете) области R. Важно отметить, что понятие «ближайшая точка» зависит от определения расстояния, и поэтому на результаты операции ПСО будет влиять выбор метрики. Хотя ПСО дает довольно удовлетворительный скелет обла­сти, его прямое применение затруднительно с вычислительной точки зрения, поскольку требуется определение расстояния между каждой точкой области и границы. Был предложен ряд алгоритмов построения средних осей, обладающих большей вычислительной эффективностью. Обычно это алгоритмы про­реживания, которые итеративно устраняют из рассмотрения точки контура области так, чтобы выполнялись следующие ограничения:

1) не устранять крайние точки;

2) не приводить к нарушению связности;

3) не вызывать чрезмерного размывания области.

 

Применение градиента

Когда сцена задана вокселами, ее можно описать плоскими участками с помощью трехмерного градиента. В этом случае дескрипторы поверхности также получаются в результате объединения этих плоских участков. Вектор градиента указывает направление максимальной скорости из­менения функции, а его величина соответствует величине этого изменения. Эти понятия применимы для трехмерного случая и также могут быть использованы для разбиения на сегменты трехмерных структур тем же способом, который применялся для двумерных данных.

Разметка линий и соединений

Итак, контуры в трехмерной сцене определяются разры­вами в данных о координатах и/или интенсивности. После того как был определен набор поверхностей и контуров, распола­гающихся между ними, окончательное описание сцены может быть получено путем разметки линий, которые соответствуют контурам, и соединений, которые эти контуры образуют.

Выпуклая линия (помеченная +) образуется в результате пересечения двух поверхностей выпуклого тела (например, линия, образо­ванная в результате пересечения двух сторон куба). Вогнутая линия (помеченная —) образуется в результате пересечения двух поверхностей, принадлежащих двум различным телам (например, пересечение стороны куба с полом). Скрытые ли­нии (помеченные стрелками) представляют собой контуры не­видимых поверхностей. Поверхности, закрывающие другие части объекта, располагаются справа направлении стрелок, а невидимые слева. После того как линии сцены дают ключ к пониманию природы трехмерных объ­ектов сцены. Физические ограничения допускают лишь несколько возмож­ных комбинаций меток линий в соединении. На­пример, сцена в виде мно­гогранника не имеет ли­ний, метки которых могут меняться между вершина­ми. Нарушение этого пра­вила приводит к объек­там, не имеющим физиче­ского смысла.

Обобщенные конусы

Обобщенным конусом (или цилиндром) называется поверх­ность, получаемая в результате перемещения плоского попереч­ного сечения вдоль произвольной пространственной кривой (хребта) под постоянным к ней углом, причем поперечное се­чение преобразуется по правилу заметания объема. В техниче­ском зрении метод обобщенных конусов независимо от других методов позволяет создавать образы трехмерных структур, что полезно при моделировании и для проверки соответствия по­строенных моделей исходным данным.

Распознавание

Распознаванием называется процесс разметки, т.е. алгоритмы распознавания идентифицируют каждый объект сцены и присваивают ему метки (гаечный ключ, перемычка). Обычно в большинстве промышленных систем технического зрения предполагается, что объекты сцены сегментированы как отдельные элементы. Другое общее ограничение относится к расположению устройств сбора информации относительно исследуемой сцены (обычно они располагаются перпендикулярно рабочей поверхности). Это приводит к уменьшению отклонений в характеристиках формы, а также упрощает процесс сегментации и описания в результате уменьшения вероятности загораживания одних объектов другими. Управление отклонениями в ориентации объекта производится путем выбора дескрипторов, инвариантных к вращению, или путем использования главных осей объекта для ориентирования его в предварительно определенном направлении.

Современные методы распознавания делятся на две основные категории: теоретические и структурные методы. Теоретические методы основываются на количественном описании (статическая структура), а в основе структурных методов лежат символические описания и их связи (последовательности направлений в границе, закодированной с помощью цепного кода).

 

Интерпретация

Интерпретацию - про­цесс, который позволяет системе технического зрения приоб­рести более глубокие знания об окружающей среде по сравне­нию со знаниями, полученными с помощью методов, изложенных выше. Рассматриваемая с этой точки зрения интерпретация охватывает данные методы как неотъемлемую часть процесса понимания зрительной сцены. Хотя в области технического зре­ния она и является объектом активных исследований, достиже­ния пока весьма незначительны. Ниже мы кратко рассмотрим проблемы, представляющие современные исследования в этой области технического зрения.

Мощность системы технического зрения определяется ее способностью выделять из сцены значимую информацию при различных условиях наблюдения и использовании минимальных знаний об объектах сцены. По ряду причин (неравномерное освещение, наличие тел, загораживающих объекты, геометрии наблюдения) этот тип обработки представляет трудную задачу. Много внимания уделено методам уменьшения раз­броса в интенсивности. Способы обратного и структурирован­ного освещения позволяют устра­нить трудности, связанные с произвольным освещением ра­бочего пространства. К этим трудностям относятся теневые аффекты, усложняющие процесс определения контуров, и неодно­родности на гладких поверхностях. Это часто Приводит к тому, что они распознаются как отдельные объекты. Очевидно, многие из этих проблем обусловлены тем, что относительно мало из­вестно о моделировании свойств освещения и отражения трех­мерных сцен. Методы разметки линий и соединений представляют собой некоторые попытки в этом направлении, но они не в состоянии количественно объяснить эффекты взаимодействия освещения и отражения. Более пер­спективный подход основан на математических моделях, опи­сывающих наиболее важные связи между освещением, отраже­нием и характеристиками поверхности, такими, как ориентация.

Проблема загораживания одних объектов другими имеет ме­сто, когда рассматривается большое число объектов в реальном рабочем пространстве. Даже если бы система была способна идеально выделить группу объектов из фона, то все ранее рассмотренные двумерные про­цедуры описания и распознавания дали бы плохой результат для большинства загороженных объектов. Применение трех­мерных дескрипторов было бы более успешным, но даже они дали бы неполную информацию.

Для обработки сцен требуются описания, которые должны содержать информацию о формах и объемах объектов, а также процедуры для установления связей между этими описаниями, даже когда они не яв­ляются полными. Несомненно, эти проблемы будут решены только путем разработки методов, позволяющих обрабатывать трехмерную информацию (полученную либо в результате не­посредственных измерений, либо с помощью геометрических ме­тодов вывода) и устанавливать (необязательно количественно) трехмерные связи на основе информации об интенсивности образа.

Знание о том, в каких случаях интерпретация сцены или части сцены является невоз­можной, так же важно, как и правильный анализ сцены. Про­смотр сцены из различных точек решил бы эту проблему и был бы естественной реакцией интеллектуального наблюдателя.

В этом направлении одним из наиболее перспективных под­ходов являются исследования в области технического зрения, основанного на моделях . Основной идеей метода является интерпретация сцены на основе обнаружения отдельных слу­чаев соответствия между данными образа и трехмерными мо­делями простейших объемных элементов или же целых объек­тов, представляющих интерес. Зрение, основанное на трехмер­ных моделях, имеет другое важное преимущество: оно дает воз­можность обрабатывать несоответствия в геометрии наблю­дения. Изменчивость образа объекта, наблюдаемого из раз­личных положений, является одной из наиболее серьезных проб­лем технического зрения. Даже для двумерных случаев, где определена геометрия наблюдения, ориентация объекта может сильно влиять на процесс распознавания, если он не управ­ляется соответствующим образом. Одно из преимуществ подхода, основанного на моделях, состоит в том, что в зависимости от известной геометрии наблюдения можно подбирать ориентацию трехмерных моделей с целью упрощения соответствия между неизвестным объектом и тем, что система видит из данной точки наблюдения.

 

Выводы

Основное внимание уделено понятиям и методам технического зрения, применяемым в промышленных приложениях. Сегментация является одним из наиболее важных процессов на ранней стадии распознавания образов системой технического зрения. Следующей задачей системы технического зрения является образование набора дескрипторов, который полностью идентифицирует объекты определенного класса. Обычно стремятся выбирать дескрипторы, наименее зависящие от размеров объекта, его ориентации и расположения. Хотя зрение и является трехмерной задачей, большинство современных промышленных систем работает с данными, которые часто упрощаются с помощью методов специального освещения или строго определенной геометрии наблюдения. Сложности возникают, когда эти ограничения ослабляются.

По существу зрение яв­ляется трехмерной проблемой, поэтому в основе разработки многофункциональных систем технического зрения, пригодных для работы в различных средах, лежит процесс обработки информации о трехмерных сценах. Хотя исследования в этой области имеют более чем 10-летнюю историю, такие факторы, как стоимость, скорость и сложность, тормозят внедрение обра­ботки трехмерной зрительной информации в промышленных приложениях. Мощность системы технического зрения определяется ее способностью выделять из сцены значимую информацию при различных условиях наблюдения и использовании минимальных знаний об объектах сцены. По ряду причин (неравномерное освещение, наличие тел, загораживающих объекты, геометрии наблюдения) этот тип обработки представляет трудную задачу. К этим трудностям относятся теневые аффекты, усложняющие процесс определения контуров, и неодно­родности на гладких поверхностях. Это часто приводит к тому, что они распознаются как отдельные объекты. Очевидно, многие из этих проблем обусловлены тем, что относительно мало из­вестно о моделировании свойств освещения и отражения трех­мерных сцен. Методы разметки линий и соединений представляют собой некоторые попытки в этом направлении, но они не в состоянии количественно объяснить эффекты взаимодействия освещения и отражения. Более пер­спективный подход основан на математических моделях, опи­сывающих наиболее важные связи между освещением, отраже­нием и характеристиками поверхности, такими, как ориентация.

Проблема загораживания одних объектов другими имеет ме­сто, когда рассматривается большое число объектов в реальном рабочем пространстве. Даже если бы система была способна идеально выделить группу объектов из фона, то все ранее рассмотренные двумерные про­цедуры описания и распознавания дали бы плохой результат для большинства загороженных объектов. Применение трех­мерных дескрипторов было бы более успешным, но даже они дали бы неполную информацию.

Разработка методов обра­ботки трехмерной зрительной информации в роботизированных и автоматизированных системах в настоящее время задача актуальная, так как такие факторы, как стоимость, скорость, сложность вычислений, трудность реализации алгоритмов делают неприемлемыми многие уже существующие методы.

 

 

Список литературы

1. Анисимов Б.В., Курганов В.Д. Распознавание и цифровая обработка изображений.

2. Гонсалиес, Фу, Ли. Робототехника.

3. Катыс Г.П. Техническое зрение роботов.

 

 

Содержание

1.ВВЕДЕНИЕ                                                                                               1

2.СЕГМЕНТАЦИЯ                                                                                      2

2.1.Проведение контуров и определение границы                                    2

2.1.1.Локальный анализ.                                                                              3

2.1.2.Глобальный анализ с помощью преобразования Хоуга.               4

2.2.Определение порогового уровня                                                           7

2.2.1.Глобальные и локальные пороги.                                                     8

2.2.3.Определение порогового уровня на основе характеристик границы. 10

2.2.4.Определение порогового уровня, основанное на нескольких переменных.                                                                                                                        12

2.3.Областно-ориентированная сегментация                                           13

2.3.1.Основные определения.                                                                      13

2.3.2.Разбиение и объединение области.                                                    16

2.4. Применение движения                                                                          17

2.4.1.Основной подход.                                                                                17

2.4.2.Аккумулятивная разность.                                                               19

2.4.3.Определение эталонного образа.                                                      22

3.ОПИСАНИЕ                                                                                              23

3.1.Дескрипторы границы.                                                                         23

3.1.1.Цепные коды.                                                                                      23

3.1.2.Сигнатуры.                                                                                          24

3.1.3.Аппроксимация многоугольниками.                                               25

3.2.Дескрипторы области                                                                            27

3.2.1.Некоторые простые дескрипторы.                                                   27

3.2.2.Текстура.                                                                                              28

3.2.3.Скелет области.                                                                                   28

4.СЕГМЕНТАЦИЯ И ОПИСАНИЕ ТРЕХМЕРНЫХ СТРУКТУР      29

4.1.Описание трехмерной сцены плоскими участками                          30

4.2. Применение градиента                                                                         30

4.3. Разметка линий и соединений                                                             30

4.4. Обобщенные конусы                                                                            31

5.Распознавание                                                                                 31

6.Интерпретация                                                                                 32

7.Выводы                                                                                                  34

Список литературы

 

 

Техническое зрение роботов

ВВЕДЕНИЕ

С целью классификации методов и подходов, используемых в си­стемах технического зрения, зрение разбито на три ос­новных подкласса: зрение низкого, среднего и высокого уров­ней. Системы технического зрения низкого уровня предназначены для обработки информа­ции с датчиков очувствления.

Эти системы можно отнести к классу «интеллектуальных» машин, если они обладают следующими признаками (призна­ками интеллектуального поведения):

1) возможностью выделения существенной информации из множества независимых признаков;

2) способностью к обучению на примерах и обобщению этих знаний с целью их применения в новых ситуациях;

3) возможностью восстановления событий по неполной ин­формации;

4) способностью определять цели и формулировать планы для достижения этих целей.

Создание систем технического зрения с такими свойствами для ограниченных видов рабочего пространства в принципе воз­можно, но характеристики таких систем далеки от возможностей человеческого зрения. В основе технического зрения лежит аналитическая формализация, направленная на решение конкрет­ных задач. Машины с сенсорными характеристиками, близкими к возможностям человека, по-видимому, появятся еще не скоро. Однако отметим, что копирование природы не является единст­венным решением этой проблемы. Читателю наверняка известны ранние экспериментальные образцы аэропланов с машущими крыльями и другими особенностями полета птиц. Современное решение задачи о полете в пространстве в корне отличается от решений, подсказанных природой. По скорости и достижимой высоте самолеты намного превосходят возможности птиц.

Системы технического зрения среднего уровня связаны с задачами сегментации, описания и распознавания отдельных объектов. Эти задачи охватывают множество подходов, ос­нованных на аналитических представлениях. Системы техниче­ского зрения высокого уровня решают проблемы, рассмотренные выше. Для более ясного понимания проблем технического зре­ния высокого уровня и его связи с техническим зрением низкого и среднего уровней введем ряд ограничений и упростим решае­мую задачу.

 

СЕГМЕНТАЦИЯ

Сегментацией называется процесс подразделения сцены на составляющие части или объекты. Сегментация является одним из основных элементов работы автоматизированной системы технического зрения, так как именно на этой стадии обработки объекты выделяются из сцены для дальнейшего распознавания и анализа. Алгоритмы сегментации, как правило, основываются на двух фундаментальных принципах: разрывности и подобии. В первом случае основной подход основывается на определении контуров, а во втором — на определении порогового уровня и расширении области. Эти понятия применимы как к статиче­ским, так и к динамическим (зависящим от времени) сценам. В последнем случае движение может служить мощным средст­вом для улучшения работы алгоритмов сегментации.

Проведение контуров и определение границы

Методы - вычисление градиента, пороговое разделение - определяют разрывы в интенсивности представления образа объекта. В идеальном слу­чае эти методы определяют пикселы, лежащие на границе меж­ду объектом и фоном. На практике данный ряд пикселов редко полностью характеризует границу из-за шума, разрывов на гра­нице вследствие неравномерной освещенности и других эффек­тов, приводящих к размытию изображения. Таким образом, ал­горитмы обнаружения контуров сопровождаются процедурами построения границ объектов из соответствующих последователь­ностей пикселов. Ниже рассмотрено несколько методик, при­годных для этой цели.

Локальный анализ.

Одним из наиболее простых подходов соединения точек контура является анализ характеристик пик­селов в небольшой окрестности (например, в окрестности раз­мером 3 X 3 или 5 X 5) каждой точки (х, у) образа, который уже подвергся процедуре обнаружения контура. Все точки, яв­ляющиеся подобными (определение критерия подобия дано ниже), соединяются, образуя границу из пикселов, обладающих некоторыми общими свойствами.

При таком анализе для установления подобия пикселов кон­тура необходимо определить:

1 )    величину градиента, требуемого для построения контурного пиксела,

 2) направление градиен­та.

Первая характеристика обозначается величиной G{f(x, у)] .

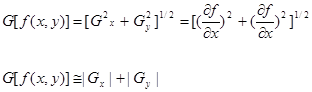
Таким образом, пиксел контура с координатами (х', у') подобен по величине в определенной ранее окрестности (х, у) пикселу с координатами (х, у), если справедливо неравенство

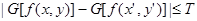
где Т —пороговое значение.

Направление градиента устанавливается по углу вектора градиента, определенного в уравнении

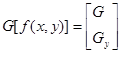
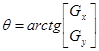
где q—угол (относительно оси х), вдоль которого скорость изменения имеет наибольшее значение. Тогда можно сказать, что угол пиксела контура с координатами { х', у') в некоторой окрестности (х, у) подобен углу пиксела с координатами { х, у) при выполнении следующего неравенства:

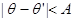
где А—пороговое значение угла. Необходимо отметить, что на­правление контура в точке { х, у) в действительности перпенди­кулярно направлению вектора градиента в этой точке. Однако для сравнения направлений неравенство  дает эквивалент­ные результаты.

Основываясь на этих предположениях, мы соединяем точку в некоторой окрестности (х, у) с пикселом, имеющим коорди­наты (х, у), если удовлетворяются критерии по величине и направлению. Двигаясь от пиксела к пикселу и представляя каждую присоединяемую точку как центр окрестности, процесс повторяется для каждой точки образа. Для установления соот­ветствия между уровнями интенсивности освещения и последо­вательностями пикселов контура применяется стандартная биб­лиотечная процедура.

Цель состоит в определении размеров прямоугольни­ков, с помощью которых можно построить качественное изобра­жение. Построение таких прямоугольников осуществляется в ре­зультате определения строго горизонтальных и вертикальных контуров. Дальнейший процесс состоял в соединении сегментов контура, разделенных небольшими промежутками, и в объединении отдельных корот­ких сегментов.

2.1.2.Глобальный анализ с помощью преобразования Хоуга.

Рас­смотрим метод соединения граничных точек путем определения их расположения на кривой специального вида. Первоначально предполагая, что на плоскости ху образа дано п точек, требуется найти подпоследовательности точек, лежащих на прямых линиях. Одно из возможных решений состоит в построении всех линий, проходящих через каждую пару точек, а затем в нахож­дении всех подпоследовательностей точек, близких к определен­ным линиям. Задача, связанная с этой процедурой, заключается в нахождении п(п— 1)/2 ~ п² линий и затем в осуществлении п [п(п—1)]/2 ~ п ³ сравнений каждой точки со всеми линиями. Этот процесс трудоемок с вычислительной точки зрения за ис­ключением самых простых приложений.

Данную задачу можно решить по-другому, применяя подход, предложенный Хоугом и называемый преобразованием Хоуга. Рассмотрим точку (х_i y_i) и общее уравнение прямой ли­нии у:= аx _i + b_i. Имеется бесконечное число линий, проходящих через точку (х_i y_i), но все они удовлетворяют уравнению у:= аx _i + b_i при различных значениях а и b. Однако, если мы за­пишем это уравнение в виде b = -х_i а + y_i и рассмотрим пло­скость а b (пространство параметров), тогда мы имеем уравне­ние одной линии для фиксированной пары чисел (х_i y_i). Более того, вторая точка (х _j, у _j) также имеет в пространстве пара­метров связанную с ней линию, которая пересекает другую ли­нию, связанную с точкой (х_i y_i) в точке (а', b’), где значения а' и b’—параметры линии, на которой расположены точки (х_i y_i) и (х_j, у _j) в плоскости ху. Фактически все точки, расположен­ные на этой линии, в пространстве параметров будут иметь ли­нии пересечения в точке (а', b’).

Вычислительная привлекательность преобразования Хоуга заключается в разделении пространства параметров на так на­зываемые собирающие элементы , где (a_макс, а_мин) и (b_макс, b_мин)—допустимые величины параметров линий. Собирающий элемент A (i, j) соответствует площади, связанной с ко­ординатами пространства параметров (а_i, b_j). Вначале эти элементы считаются равными нулю. Тогда для каждой точки (x_k, у _k) в плоскости образа мы полагаем параметр а равным каж­дому из допустимых значений на оси а и вычисляем соответст­вующее b, используя уравнение b = -х _k + y _k Полученное значение b затем округляется до ближайшего допустимого зна­чения на оси b. Если выбор a_р приводит к вычислению b_q, мы полагаем А(р, q) ==А(р, q) + 1. После завершения этой про­цедуры значение М в элементе A (i, j) соответствует М точкам в плоскости xy, лежащим на линии y= a_ix+b. Точность рас­положения этих точек на одной прямой зависит от числа раз­биений плоскости аb. Отметим, что, если мы разбиваем ось а на К частей, тогда для каждой точ­ки (x_k, у _k) мы получаем К зна­чений b, соответствующих К воз­можным значениям а. Посколь­ку имеется п точек образа, про­цесс состоит из пК вычислитель­ных операций. Поэтому приве­денная выше процедура линейна относительно п и имеет меньшее число вычислительных опера­ций, чем процедура, описанная выше, если К<= п.

Проблема, связанная с пред­ставлением прямой линии урав­нением у = ах + b, состоит в том, что оба параметра а и b стремятся к бесконечности, если линия принимает вертикаль­ное положение. Для устранения этой трудности используется нормальное представление прямой линии в виде

xcos q +ysin q = b .        

Это представление для построения таблицы собирающих элементов используется так же, как метод, изложенный выше, но вместо прямых линий мы имеем синусоидальные кривые в плоскости q r. Как и прежде, М точек, лежащих на прямой xcos q _i+уsinq_i == r _i , соответствуют М синусоидальным кривым, кото­рые пересекаются в точке (q _i, r _i) пространства параметров. Если используется метод возрастания q и нахождения для него соот­ветствующего r, процедура дает М точек в собирающий элемент А (i, j), связанный с точкой (q _i, r _i).