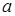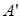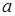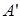Блок 1 - Начало программы
Блок 2 - Процедура ввод статистических коэффициентов оптимизации
Блок 3 - Основная процедура расчета по методу Гурвица
Блок 4 - Оператор вывода расчетных таблиц
Блок 5 - Процедура вывода расчетной таблицы и платежной матрицы игрока А
Блок 6 - Процедура вывода расчетной таблицы и платежной матрицы игрока В
Блок 7 - Конец программы
2.5.2. Описания основной процедуры W_rezultat расчета по методу Гурвица
Блок 1 - Вход в процедуру
Блок 2 - Начало цикла i от 1 до m
Блок 3 - Начало цикла j от 1 до n
Блок 4 - Преобразования символа строки из ячейки таблицы C_S в целое число матрицы C_a
Блок 5 - Конец цикла по j
Блок 6 - Конец цикла по I
Блок 7 - Начало цикла i от 1 до n
Блок 8 - Начало цикла j от 1 до m
Блок 9 - Преобразования символа строки из ячейки таблицы C_S в целое число матрицы С_b
Блок 10 - Конец цикла по j
Блок 11 - Конец цикла по I
Блок 12 - Начало цикла i от 1 до m
Блок 13 - Массиву a_m (наименьшие выигрыши)присваивается первый элемент i строки матрицы С_a (игрока А)
Блок 14 - Массиву a_b (наибольшие выигрыши)присваивается первый элемент i строки матрицы С_a (игрока А)
Блок 15 - Начало цикла j от 2 до n
Блок 16 - Проверка условия на нахождения минимального элемента
Блок 17 - Нахождения минимального элемента
Блок 18 - Проверка условия на нахождения максимально элемента
Блок 19 - Нахождения максимально элемента
Блок 20 - Конец цикла по j
Блок 21 - Начало цикла j от 1 до k
Блок 22 - Расчет условно расчетных выигрышей (игрока А)
Блок 23 - Конец цикла по j
Блок 24 - Конец цикла по i
Блок 25 - Максимальному выигрышу max_a присваивается первый элемент первой строки матрицы условно расчетных выигрышей (игрока А)
Блок 26 - Оптимальной стратегии H_a присваивается первая стратегия (игрока А)
Блок 27 - Начало цикла i от 1 до m
Блок 28 - Начало цикла j от 1 до k
Блок 29 - Проверка условия на нахождения максимально выигрыша
Блок 30 - Нахождения максимально выигрыша
Блок 31 - Нахождения оптимальной стратегии
Блок 32 - Конец цикла по j (игрока А)
Блок 33 - Конец цикла по I (игрока А)
Блок 34 - Начало цикла i от 1 до n
Блок 35 - Массиву b_m (наименьшие выигрыши)присваивается первый элемент i строки матрицы С_b (игрока В)
Блок 36 - Массиву b_b (наибольшие выигрыши)присваивается первый элемент i строки матрицы С_b (игрока В)
Блок 38 - Проверка условия на нахождения минимального элемента
Блок 39 - Нахождения минимального элемента
Блок 40 - Проверка условия на нахождения максимально элемента
Блок 41 - Нахождения максимально элемента
Блок 44 - Расчет условно расчетных выигрышей (игрока В)
Блок 47 - Максимальному выигрышу max_b присваивается первый элемент первой строки матрицы условно расчетных выигрышей (игрока B)
Блок 48 - Оптимальной стратегии H_b присваивается первая стратегия (игрока B)
Блок 51 - Проверка условия на нахождения максимально выигрыша
Блок 52 - Нахождения максимально выигрыша
Блок 53 - Нахождения оптимальной стратегии
Блок 56 - Проверка условия на наличие седловых точек
Блок 58 - Проверка условия на нахождения игрока, разрешающего конфликтную ситуацию
Блок 59 - Вывод игрока А разрешивший конфликтную ситуацию
Блок 60 - Вывод игрока В разрешивший конфликтную ситуацию
Блок 61 - Вывод оптимальной стратегии и набольшего выигрыша игрока А
Блок 62 - Вывод оптимальной стратегии и набольшего выигрыша игрока В
Блок 63 - Выход из процедуры
Характеристика программы
Программа написана на языке Object Pascal. Она занимает 44,8 Кб оперативной памяти, место на жестком диске 498 Кб. Программа была реализована на компьютере Intel Celeron 366 с помощью OC Windows’ 98, в среде программирования Delphi версия 5.0.
Выходными данными является платёжная матрица, состоящая из вещественных чисел и коэффициенты оптимизма – целые числа. Эти данные будут вводиться пользователем с клавиатуры и идентифицироваться в окне на экране монитора.
Выходными данными будет расчетные таблицы для игроков А и В, максимальный выигрыш, оптимальная стратегия каждого из игроков, а также будет выведен игрок, разрешающий конфликтную ситуацию.
Описание процесса отладки
Под отладкой понимается процесс поиска и устранения ошибок в программе. Ошибки, которые могут быть в программе, принято делить на три группы: синтаксические ошибки; ошибки времени выполнения; алгоритмические ошибки.
В среде Delphi мощный встроенный отладчик, значительно упрощающий отладку программ.
Основными инструментами отладки является точки контрольного останова и окно наблюдения за переменными. Если программа запущена из среды Delphi, ее работу можно прервать в любой момент или установив точку контрольного останова в той части программы, которая выполняется в данный момент или будет выполнена.
После контрольного останова в окне наблюдения отображаются текущие значения наблюдаемых объектов. Кроме того, можно увидеть текущее значение любой переменной, если в окне редактора укажете на нее мышью.
Для написания моей программы использовался метод тестирования. Метод тестирования основан на обдумываний и заключается в использования тестов. Существую два типа тестов: тесты для тестирования целью которых является обнаруживания заранее не определенной ошибки и тесты для отладки, цель которых обеспечить информации полезной для выявления место нахождения подозреваемой ошибки.
Результаты решения задачи
Разрешить конфликтную ситуацию двух игроков А и В заданную в неопределенных условиях с статистические коэффициентами оптимизации 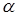 =0,1;
=0,1; 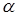 =0,2;
=0,2; 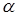 =0,3.
=0,3.
Исходные данные и решения задачи сводится в таблицу 2.8.1.
Таблица 2.8.1
|
| В1 | В2 | В3 | Наименьший выигрыш
| Наибольший выигрыш
| Коэффициенты оптимизма | ||
| 0,1 | 0,2 | 0,3 | ||||||
| А1 | 1 | 1 | 3 | 1 | 3 | 2,8 | 2,6 | 2,4 |
| А2 | 5 | 6 | 8 | 5 | 8 | 7,7 | 7,4 | 7,1 |
| А3 | 4 | 3 | 5 | 3 | 5 | 4,8 | 4,6 | 4,4 |
Найти игрока, разрешающего конфликтную ситуацию.
Найдём условно расчётные выигрыши игрока А по формуле:
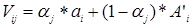
V11=0,1*1+(1 – 0,1)*3=2,8
V12=0,2*1+(1 – 0,2)*3=2,6
V13=0,3*1+(1 – 0,3)*3=2,4
V21=0,1*5+(1 – 0,1)*8=7,7
V22=0,2*5+(1 – 0,2)*8=7,4
V23=0,3*5+(1 – 0,3)*8=7,1
V31=0,1*3+(1 – 0,1)*5=4,8
V32=0,2*3+(1 – 0,2)*5=4,6
V33=0,3*3+(1 – 0,3)*5=4,4
Среди найденных условных расчётных выигрышей найдём максимальный. Он равен 7.7, значит оптимальная стратегия игрока А будет А2.
Далее найдём оптимальная стратегия игрока В, для этого транспонируем матрицу. Результаты заносим в таблицу 2.8.2.
Таблица 2.8.2
|
| А1 | А2 | А3 | Наименьший выигрыш
| Наибольший выигрыш
| Коэффициенты оптимизма | ||
| 0,1 | 0,2 | 0,3 | ||||||
| В1 | 1 | 5 | 4 | 1 | 5 | 4,6 | 4,2 | 3,8 |
| В2 | 1 | 6 | 3 | 1 | 6 | 5,5 | 5 | 4,5 |
| В3 | 3 | 8 | 5 | 3 | 8 | 7,5 | 7 | 6,5 |
Найдём условно расчётные выигрыши игрока В
V11=0,1*1+(1 – 0,1)*5=4,6
V12=0,2*1+(1 – 0,2)*5=4,2
V13=0,3*1+(1 – 0,3)*5=3,8
V21=0,1*1+(1 – 0,1)*6=5,5
V22=0,2*1+(1 – 0,2)*6=5
V23=0,3*1+(1 – 0,3)*6=4,5
V31=0,1*3+(1 – 0,1)*8=7,5
V32=0,2*3+(1 – 0,2)*8=7
V33=0,3*3+(1 – 0,3)*8=6,5
Среди найденных условных расчётных выигрышей найдём максимальный. Он равен 7.5, значит оптимальная стратегия игрока В будет В3.
Из 2-х оптимальных стратегий, находим наибольший выигрыш, а именно 7,7>7,5; следовательно игрок А разрешит конфликтную ситуацию с максимальным выигрышем равным 7,7, стратегия которого равна 2.
Дата: 2019-07-24, просмотров: 277.