СОДЕРЖАНИЕ
ВВЕДЕНИЕ.. 2
1... ОБЩАЯ ЧАСТЬ.. 3
1.1. Цель разработки. 3
1.2. Анализ использования разработки. 3
1.3. Анализ методов решения задачи. 3
1.4. Анализ средств программирования. 4
1.4.1. Обзор средств программирования. 4
1.4.2. Характеристика программного обеспечения. 4
1.4.3. Характеристика ПК. 6
1.4.4. Характеристика языка программирования. 6
2... СПЕЦИАЛЬНАЯ ЧАСТЬ.. 8
2.1. Постановка задачи. 8
2.2. Экономико – математическая модель. 12
2.3. Описания метода Гурвица. 13
2.4. Алгоритм задачи. 14
2.4.1. Алгоритм основной программы.. 14
2.4.2. Алгоритм процедуры W_rezultat 15
2.5. Описание алгоритма. 21
2.5.1. Описание алгоритма основной программы.. 21
2.5.2. Описания основной процедуры W_rezultat расчета по методу Гурвица 21
2.6. Характеристика программы.. 24
2.7. Описание процесса отладки. 24
2.8. Результаты решения задачи. 25
2.9. Оценки результатов решения задачи. 27
ЗАКЛЮЧЕНИЕ.. 28
СПИСОК ЛИТЕРАТУРЫ... 29
Приложение 1 Текст программы.. 30
Приложение 2. Результаты работы программы.. 36
ВВЕДЕНИЕ
В курсовом проекте представлена задача теория игр.
Одним из разделов теории игр являются состязательные задачи в условиях неопределённости. Состязательные задачи – это задачи, в которых сталкиваются интересы 2-х или более сторон, преследующих различные цели. Для решения этих задач используется методы теории игр. Для состязательных задач в условиях неопределённости в теории игр разработаны соответствующие принципы, на основании которых неопределенные ситуации преобразуется в детерминированные и решаются методом максимина.
Согласно принципу Гурвица неразумно, приняв во внимание самый маленький выигрыш, не учитывать самый большой, для чего необходимо ввести коэффициенты оптимизма (он выполняет роль вероятности). Значения оптимизма выбирают на основании субъективных соображений. В технических приложениях сложно выбрать коэффициент оптимизма, т.к. трудно найти количественную характеристику для тех долей оптимизма и пессимизма, которые присутствуют при принятии решения. Принцип Гурвица учитывает как пессимистический, так и оптимистический подход к ситуации.
ОБЩАЯ ЧАСТЬ
Цель разработки
Данный курсовой проект разрабатывался с целью вывести ситуацию из условия неопределённости; найти максимальный выигрыш, по которому определить оптимальную стратегию каждого игрока и игрока разрешающего конфликтную ситуацию.
Анализ использования разработки
Данный курсовой проект предназначен для прогнозирования в учебных заведениях
Анализ методов решения задачи
Для решения состязательных задач в условиях неопределённости в теории игр разработаны соответствующие принципы, на основании которых неопределенные ситуации преобразуются в детерминированные условия и решаются следующими методами: метод максимина, метод минимакса, принцип Гурвица, метод Сэвиджа, метод Бейеса-Лапласа. В данном курсовом проекте использовался принцип Гурвица.
Анализ средств программирования
Обзор средств программирования
Данную программу можно написать на различный языках программирования : Си, Бейсик, Ассемблер т. д. В данной случае выбран язык Object Pascal(доработанная разновидность языка Pascal), т.к. он отличен от Бейсика и Ассемблера тем, что среда разработки Delphi имеет широкие возможности визуальной разработки (разработчик во время разработки может видеть интерфейс своей программы и размещать на ней компоненты ) и интеллектуальную систему отладки. Язык Ассемблер является неудобным в данном случае, а в языке Бейсик ограничены возможности применения процедур и функций, При написании программы на языке Object Pascal используются все возможности модульности программ, процедуры и функции.
Характеристика ПК
В ПК, на котором разрабатывался курсовой проект можно выделить основные части:
Монитор: Samsung Sync Master 550 (M)S, разрешающая максимальная способность 1024x768 точек на дюйм и частота обновления 75 Гц;
MB: Intel T810B-S ;
Процессор: Intel Celeron 366 (Genuine Intel Семейство 6 Модель 366 MГц Модификация 5);
SDRAM: Samsung 64Mb
HDD:4,2 Gb Quantum;
Дисководы: FDD 1,44Mb, CD-ROM 40x ;
Принтер: Epson FX-1000;
Клавиатура: Расширенная клавиатура PC/AT ( Windows’98 107 клавиш);
Мышь: Стандартная мышь для COM-порта;
СПЕЦИАЛЬНАЯ ЧАСТЬ
Постановка задачи
Теория игр – теория математических модулей, интересы участников которых различны, причём они достигают своих целей различными путями.
Столкновение противоположных интересов участников приводит к возникновению конфликтных ситуаций. Чтобы исключить трудности, возникающие при анализе конфликтных ситуаций, строится упрощенная модель ситуаций. Такая модель называется игрой. Теория игр относится к теории статистических решений.
В задачах теории игр предполагалось, что в них примут участие две стороны, интересы которых противоположны. Поэтому действия каждой стороны направлены на увеличения выигрыша. Но во многих задачах, приводящих к игровым, неопределенность вызвана отсутствием информации об условиях, в которых осуществляется действие. Эти условия зависят не от сознательных действий другого игрока, а от объективной действительности, которую принято называть природой.
Игру с природой описывается с помощью платёжной матрицы, в которой в качестве игрока А выступает статистик (человек, который принимает решения), имеющий m возможных стратегий А1, А2, …, Аm, а в качестве второго игрока выступает природа.
План, по которому игрок совершает выбор в каждой возможной ситуации и при каждой возможной фактической информации называется стратегий игрока.
Главным в исследовании теории игр является выбор оптимальных стратегий игроков. Стратегия игрока является оптимальной, если применение этой стратегии обеспечит ему наибольший гарантированный выигрыш при всевозможных стратегиях другого игрока. В процессе одной игры каждый из игроков выбирает одну стратеги. Стратегии делятся на чистые и смешанные.
Чистая стратегия – это стратегия, имеющая одно единственное значение или решение из множества заданных.
Смешанная (сложная) стратегия – это стратегия, которая берёт m значений с соответствующими вероятностями.
Стороны участвующие в конфликтной ситуации называются игроками, а предполагаемые действия каждого из игроков, направленные на достижение некоторой цели, называется правилами игры.
Платёж – это количественная оценка результатов игры.
Ходом в теории игр называется выбор одного из предложенных правилами игры действий его осуществлении.
Состязательная задача – это задача, разрешающая конфликтные ситуации между двумя или более противниками с целью нахождения оптимальной стратегии для каждого игрока, и в конечном итоге игрока, разрешающего конфликтную ситуацию.
Игру двух игроков можно описать как производственный процесс с помощью следующей функциональной схемы (рис.1).
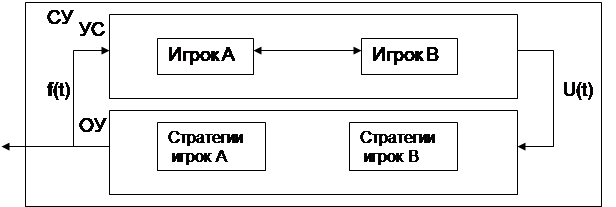 Рисунок 2.1.1
Рисунок 2.1.1
Оба игрока по прямой связи U(t) делает ход, выбирая предполагаемую стратегию. Ни один из игроков не знает хода противника. В случае если игрок узнает стратегию своего противника, то по обратной связи f(t) поступает сигнал, что он может отказаться от своей старой стратегии и выбрать другую стратегию. Востановив работу по прямой связи U(t).
Человек А в играх с природой старается действовать осмотрительно, используя, например, минимаксную стратегию, позволяющую получить наименьший проигрыш. Второй игрок В (природа) действует совершенно случайно, возможные стратегии определяются как её состояние. Условия игры задаются в виде матрицы.
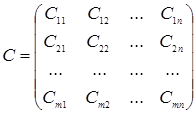
Элементы Сij = выигрышу игрока А, если он использует стратегию Аi.
В данном курсовом проекте состязательная задача решается по методу Гурвица.
Пусть в игре принимают участие два игрока А и В.
Рассматривается конфликтная ситуация между двумя сторонами А и В. Игрок А имеет m стратегий, а В имеет n стратегий: А={А1, А1,…, А1}; В={В1, В1,…, В1}.
Взаимосвязь между стратегиями любого из игроков определяется платёжной матрицей С={Cij}m*n. Cij – выигрыш игрока А. Заданы статистические коэффициенты оптимизации ( 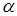 ).
).
Цель игры состоит в том, чтобы вывести ситуацию из условия неопределённости, найти максимальный выигрыш, по которому определить оптимальную стратегию каждого игрока, а также игрока разрешающего конфликтную ситуацию.
Решение игры и исходные данные сводятся в таблицу Гурвица (табл. 2.1.1).
Таблица 2.1.1
|
| В1 | В2 | … | Вn | Наименьший выигрыш | Наибольший выигрыш | Коэффициенты оптимизма | ||
 1 1
| … | 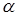 k k
| |||||||
| А1 | C11 | C12 | … | C1n | a1 | А`1 | V11 | … | V1k |
| А2 | C21 | C22 | … | C2n | a 2 | А`2 | V21 | … | V2k |
| … | … | … | … | … | … | … | … | … | … |
| Аm | Cm1 | Cm2 | … | Cmn | a m | А`m | Vm1 | … | Vmk |
Где 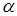 j – статистические коэффициенты оптимизации;
j – статистические коэффициенты оптимизации;
к – количество оптимизмов;
Аj – стратегии игрока А;
Вj - стратегии игрока В;
Vij – расчетные условные выигрыши;
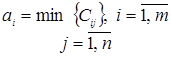
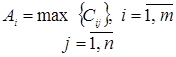
С учётом коэффициентом оптимизма вычисляем условные выигрыши
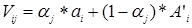
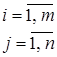
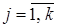
Выбираем решение о выборе стратегии, при 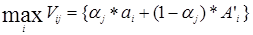 , где 0
, где 0 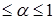 (для
(для 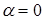 игрок переходит к стратегии «азартного игрока»; для
игрок переходит к стратегии «азартного игрока»; для 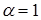 - стратегия абсолютного оптимизма).
- стратегия абсолютного оптимизма).
.
Описания метода Гурвица
Алгоритм задачи
Алгоритм основной программы
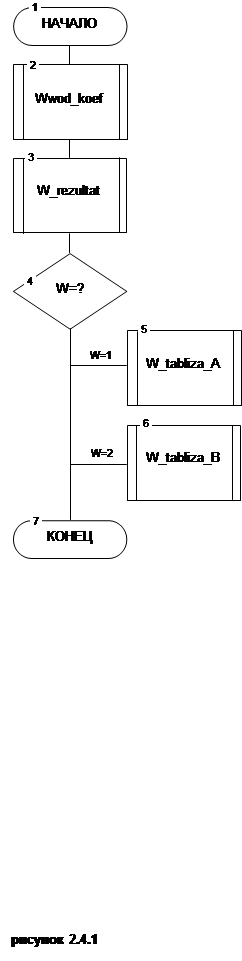
2.4.2. Алгоритм процедуры W_rezultat
 |
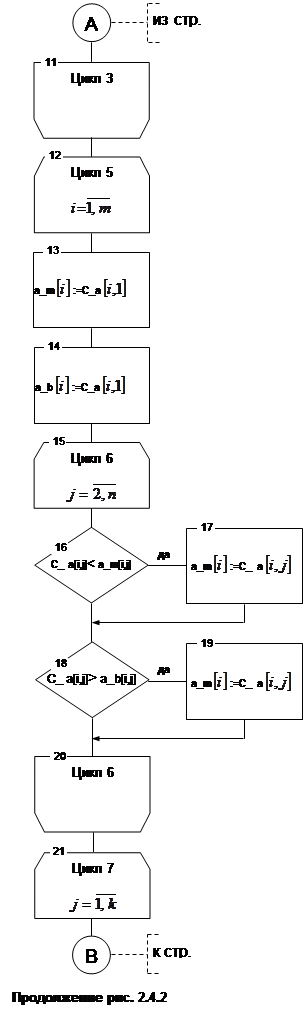 |
 |
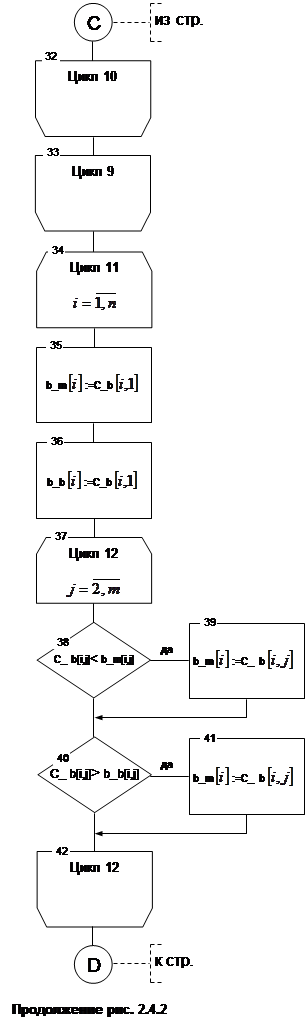 |
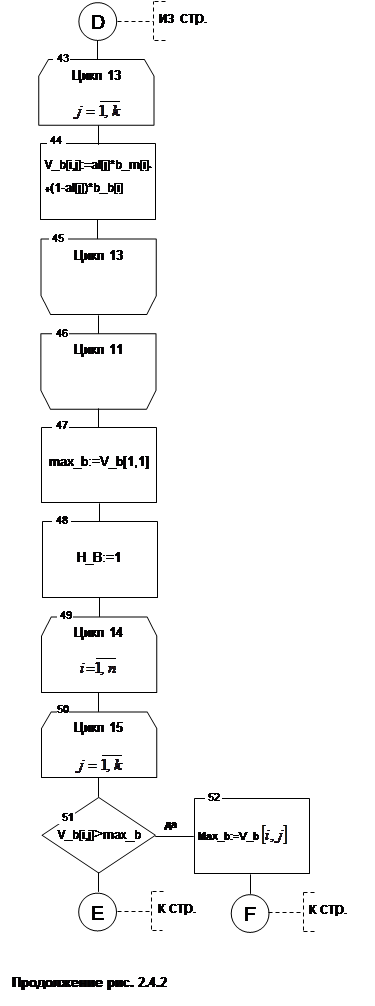
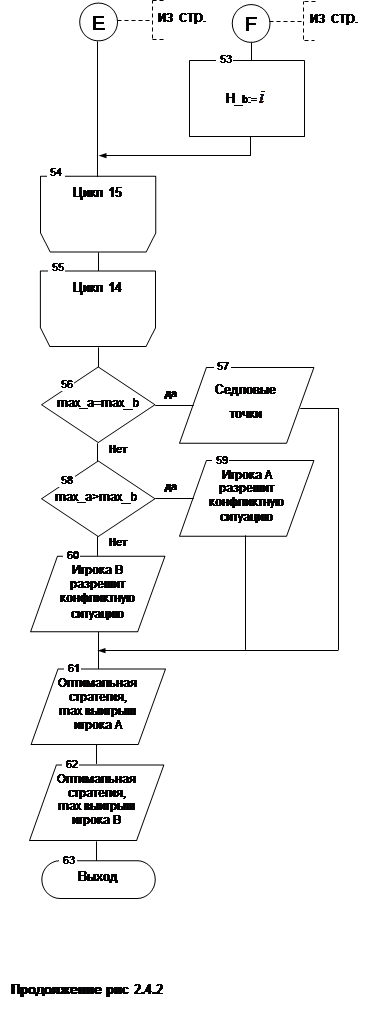 |
Описание алгоритма
Характеристика программы
Программа написана на языке Object Pascal. Она занимает 44,8 Кб оперативной памяти, место на жестком диске 498 Кб. Программа была реализована на компьютере Intel Celeron 366 с помощью OC Windows’ 98, в среде программирования Delphi версия 5.0.
Выходными данными является платёжная матрица, состоящая из вещественных чисел и коэффициенты оптимизма – целые числа. Эти данные будут вводиться пользователем с клавиатуры и идентифицироваться в окне на экране монитора.
Выходными данными будет расчетные таблицы для игроков А и В, максимальный выигрыш, оптимальная стратегия каждого из игроков, а также будет выведен игрок, разрешающий конфликтную ситуацию.
Описание процесса отладки
Под отладкой понимается процесс поиска и устранения ошибок в программе. Ошибки, которые могут быть в программе, принято делить на три группы: синтаксические ошибки; ошибки времени выполнения; алгоритмические ошибки.
В среде Delphi мощный встроенный отладчик, значительно упрощающий отладку программ.
Основными инструментами отладки является точки контрольного останова и окно наблюдения за переменными. Если программа запущена из среды Delphi, ее работу можно прервать в любой момент или установив точку контрольного останова в той части программы, которая выполняется в данный момент или будет выполнена.
После контрольного останова в окне наблюдения отображаются текущие значения наблюдаемых объектов. Кроме того, можно увидеть текущее значение любой переменной, если в окне редактора укажете на нее мышью.
Для написания моей программы использовался метод тестирования. Метод тестирования основан на обдумываний и заключается в использования тестов. Существую два типа тестов: тесты для тестирования целью которых является обнаруживания заранее не определенной ошибки и тесты для отладки, цель которых обеспечить информации полезной для выявления место нахождения подозреваемой ошибки.
Результаты решения задачи
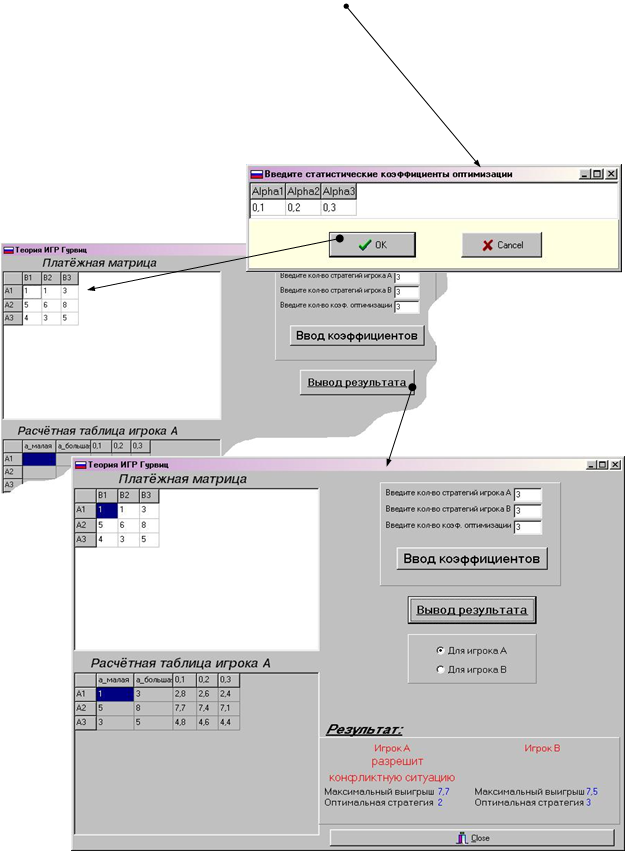
Разрешить конфликтную ситуацию двух игроков А и В заданную в неопределенных условиях с статистические коэффициентами оптимизации 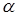 =0,1;
=0,1; 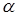 =0,2;
=0,2; 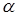 =0,3.
=0,3.
Исходные данные и решения задачи сводится в таблицу 2.8.1.
Таблица 2.8.1
|
| В1 | В2 | В3 | Наименьший выигрыш
| Наибольший выигрыш
| Коэффициенты оптимизма | ||
| 0,1 | 0,2 | 0,3 | ||||||
| А1 | 1 | 1 | 3 | 1 | 3 | 2,8 | 2,6 | 2,4 |
| А2 | 5 | 6 | 8 | 5 | 8 | 7,7 | 7,4 | 7,1 |
| А3 | 4 | 3 | 5 | 3 | 5 | 4,8 | 4,6 | 4,4 |
Найти игрока, разрешающего конфликтную ситуацию.
Найдём условно расчётные выигрыши игрока А по формуле:
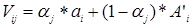
V11=0,1*1+(1 – 0,1)*3=2,8
V12=0,2*1+(1 – 0,2)*3=2,6
V13=0,3*1+(1 – 0,3)*3=2,4
V21=0,1*5+(1 – 0,1)*8=7,7
V22=0,2*5+(1 – 0,2)*8=7,4
V23=0,3*5+(1 – 0,3)*8=7,1
V31=0,1*3+(1 – 0,1)*5=4,8
V32=0,2*3+(1 – 0,2)*5=4,6
V33=0,3*3+(1 – 0,3)*5=4,4
Среди найденных условных расчётных выигрышей найдём максимальный. Он равен 7.7, значит оптимальная стратегия игрока А будет А2.
Далее найдём оптимальная стратегия игрока В, для этого транспонируем матрицу. Результаты заносим в таблицу 2.8.2.
Таблица 2.8.2
|
| А1 | А2 | А3 | Наименьший выигрыш
| Наибольший выигрыш
| Коэффициенты оптимизма | ||
| 0,1 | 0,2 | 0,3 | ||||||
| В1 | 1 | 5 | 4 | 1 | 5 | 4,6 | 4,2 | 3,8 |
| В2 | 1 | 6 | 3 | 1 | 6 | 5,5 | 5 | 4,5 |
| В3 | 3 | 8 | 5 | 3 | 8 | 7,5 | 7 | 6,5 |
Найдём условно расчётные выигрыши игрока В
V11=0,1*1+(1 – 0,1)*5=4,6
V12=0,2*1+(1 – 0,2)*5=4,2
V13=0,3*1+(1 – 0,3)*5=3,8
V21=0,1*1+(1 – 0,1)*6=5,5
V22=0,2*1+(1 – 0,2)*6=5
V23=0,3*1+(1 – 0,3)*6=4,5
V31=0,1*3+(1 – 0,1)*8=7,5
V32=0,2*3+(1 – 0,2)*8=7
V33=0,3*3+(1 – 0,3)*8=6,5
Среди найденных условных расчётных выигрышей найдём максимальный. Он равен 7.5, значит оптимальная стратегия игрока В будет В3.
Из 2-х оптимальных стратегий, находим наибольший выигрыш, а именно 7,7>7,5; следовательно игрок А разрешит конфликтную ситуацию с максимальным выигрышем равным 7,7, стратегия которого равна 2.
ЗАКЛЮЧЕНИЕ
Данная курсовая работа включает в себя два предмета: «Программирование» и «Компьютерное модулирование»
В курсовой работе были рассмотрены следующие вопросы:
· Рассмотрена характеристика «Теории игр» и следующие методы ее решения: метод Гурвица, метод Сэвиджа, метод максимина.
· Рассмотрен и дан алгоритм решения теории игры в условии неопределенности методом Гурвица.
· Дана краткая характеристика ПК, включая анализ средств программирования, описания ОС MS-DOS и MS Windows’
· Рассмотрен выбор языка программирования.
· Написана программа для решения данной задачи.
СПИСОК ЛИТЕРАТУРЫ
1. Г. С. Малик «Основы экономики и математические методы в планировании».
2. Кузнецов «Математическое программирование».
3. В. В. Фаронов «Delphi 5. Учебный курс».
4. Ю. П. Зайченко «Исследование операций в задачах, алгоритмах, программах».
Приложение 1 Текст программы
Medot_Gurwiwiza.dpr
program Medot_Gurwiza;
{Курсовой проект по предмету "Компьютерное модулирование" по теме "Теория игр"
Принцип Гурвица Выполнил студент гр. П-00-1 Юшков Андрей 10.06.02}
uses
Forms,
osnowa in 'osnowa.pas' {form1},
Unit2 in 'Unit2.pas' {Form2};
{$R *.RES}
begin
Application.Initialize;
Application.CreateForm(Tform1, form1);
Application.CreateForm(TForm2, Form2);
Application.Run;
end.
unit osnowa;
interface
uses
Windows, Messages, SysUtils, Classes, Graphics, Controls, Forms, Dialogs,
Grids, StdCtrls, ToolWin, ComCtrls, Buttons, ActnList, StdActns, Menus,
Mask, ExtCtrls, jpeg;
type
Tform1 = class(TForm)
tabliza: TStringGrid;
Panel1: TPanel;
Button1: TButton;
Edit1: TEdit;
Edit2: TEdit;
Edit3: TEdit;
Label2: TLabel;
Label3: TLabel;
Label4: TLabel;
C_S: TStringGrid;
Panel2: TPanel;
Label5: TLabel;
Label6: TLabel;
Label7: TLabel;
Label8: TLabel;
Label9: TLabel;
Label10: TLabel;
Label11: TLabel;
Label12: TLabel;
Label13: TLabel;
Label14: TLabel;
Panel3: TPanel;
Panel4: TPanel;
Label17: TLabel;
Label18: TLabel;
Panel5: TPanel;
Label19: TLabel;
Label20: TLabel;
Label21: TLabel;
Label22: TLabel;
Label23: TLabel;
RadioButton7: TRadioButton;
RadioButton8: TRadioButton;
Button3: TButton;
Panel6: TPanel;
Label1: TLabel;
BitBtn1: TBitBtn;
Label15: TLabel;
procedure WWod_koef(Sender: TObject);
procedure W_Rezultat(Sender: TObject);
procedure W_tabliza_A(Sender: TObject);
procedure W_tabliza_B(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
var
form1: Tform1;
C_B,C_A:array [1..10,1..10] of integer; { платёжная матрица игрока А,В}
a_b,a_m,b_b,b_m:array[1..10] of integer; {наибольший наименьший выигрыш иг. А,В}
al:array[1..10] of real; {массив альфа}
V_A,V_B:array[1..10,1..10]of real; {Расчётные выигрыши иг. А,В }
max_a:real; { Наибольший выигрыш игрока А}
max_b:real; { Наибольший выигрыш игрока В}
H_a:integer; { Оптимальная стратегия игрока А}
h_b:integer; { Оптимальная стратегия игрока В}
m:Integer; { Количество стратегий игрока А}
n:Integer; { Количество стратегий игрока В}
k:Integer; { Количество статистических коэффициентов}
I,J:Integer;
implementation
uses Unit2;
{$ R *. DFM }
{ вывод коэф., матрицы С_А}
procedure WW_A;
begin
form1.c_s.Colcount:=n+1;
form1.c_s.Rowcount:=m+1;
form1.tabliza.Rowcount:=m+1;
for i :=1 to m do
begin
form1.tabliza.Cells[0,i]:='A'+intToStr(i);
form1.C_S.Cells[0,i]:='A'+intToStr(i);
for j :=1 to n do
begin
form1.C_S.Cells[j,0]:='B'+intToStr(j);
form1.C_S.Cells[j,i]:=intToStr(C_A[i,j]);
end;
end;
with form1 do
begin
label23.caption:='A';
tabliza.cells[1,0]:='a_малая';tabliza.cells[2,0]:='a_большая';
end;
end;
{ Вывод наибольший, наименьший, расчётный выигрыш матрицы V _А}
procedure WW_A1;
begin
WW_A;
With form1.tabliza Do
begin
for j:=1 to n do
begin
cells[1,j]:=intToStr(a_m[j]);
cells[2,j]:=intToStr(a_b[j]);
end;
for i:=1 to m do
for j:=1 to k do
cells[j+2,i]:=floatToStr(V_a[i,j]);
end;
end;
{событие на нажатие кнопки 'Ввод коэф..'}
procedure TForm1.WWod_koef(Sender: TObject);
begin
try
m:=strToint(edit1.text);
n:=strToint(edit2.text);
k:=strToint(edit3.text);
except
showMessage('Ошибочная запись числа ');
end;
try
Form2 := TForm2.Create(self);
tabliza.Colcount:=3+k;
Form2.ShowModal;
finally
Form2.Close;
WW_a;
end;
end;
{событие на нажатие кнопки 'вывод результата'}
procedure Tform1.W_Rezultat(Sender: TObject);
begin
Panel6.Visible:=false;
panel3.Visible:=true;
{Вводим из таблицы C _ A в матрицу игрока А - C _ A } { C _ S [столбец,строка] }
for i :=1 to m do {по столбцам m таблицы C_S}
for j :=1 to n do {по строкам n таблицы C_S}
C_a[i,j]:=StrToInt(C_S.Cells[j,i]);
{Создаём матрицу C _ B путём транспонирования матрицы игрока А}
for i :=1 to n do
for j :=1 to m do
C_b[i,j] :=StrToInt(C_S.Cells[i,j]);
{расчет наименьших и наибольших выигрышей игрока A}
for i:=1 to m do
begin
a_m[i]:=C_a[i,1]; {массив наименьшии выигрыш}
a_b[i]:=C_a[i,1]; {массив наибольшии выигрыш}
for j :=2 to n do
begin
if C_a[i,j]<a_m[i] then a_m[i]:=C_a[i,j];
if C_a[i,j]>a_b[i] then a_b[i]:=C_a[i,j];
end;
{вычисления расчетных выигрышей игрока A }
for j :=1 to k do
V_a[i,j]:=al[j]*a_m[i]+(1-al[j])*a_b[i];
end;
{нахождения оптимальной стратегии и максимального выигрыша игрока A }
max_a:=V_a[1,1];
H_A:=1;
for i :=1 to m do
for j :=1 to k do
if V_a[i,j]>max_A then
begin
max_a:=V_a[i,j]; { максимальный выигрыш игрока А}
H_a:=i { оптимальная стратегия игрока А}
end;
{расчет наименьших и наибольших выигрышей игрока В}
for i:=1 to n do
begin
b_m[i]:=C_b[i,1]; {массив наименьшии выигрыш}
b_b[i]:=C_b[i,1]; {массив наибольшии выигрыш}
for j:=2 to m do
begin
if C_b[i,j]<b_m[i] then b_m[i]:=C_b[i,j];
if C_b[i,j]>b_b[i] then b_b[i]:=C_b[i,j];
end;
{вычисления расчетных выигрышей игрока В}
for j:=1 to k do
V_b[i,j]:=al[j]*b_m[i]+(1-al[j])*b_b[i];
end;
{нахождения оптимальной стратегии и максимального выигрыша игрока В}
max_b:=V_b[1,1];
H_b:=1;
for i:=1 to n do
for j:=1 to k do
if V_b[i,j]>max_b then
begin
max_b:=V_b[i,j]; { максимальный выигрыш игрока B}
H_b:=i { оптимальная стратегия игрока B }
end;
{ нахождения наибольшего расчетного выигрыша одного из игроков }
if max_a=max_b then Panel6.Visible:=true
else
if max_a>max_b then
begin
Panel4.Visible:=true;
panel5.Visible:=false
end
else
begin
panel5.Visible:=true;
Panel4.Visible:=false
end;
label11.Caption:=FloatToStr(max_a);
label12.Caption:=FloatToStr(H_a);
label14.Caption:=FloatToStr(max_b);
label13.Caption:=FloatToStr(H_b);
WW_A1;
end;
{просмотр для игрока А}
procedure Tform1.W_tabliza_A(Sender: TObject);
begin
WW_A1;
end;
{просмотр для игрока B }
procedure Tform1.W_tabliza_B(Sender: TObject);
begin
with form1 do
Begin
c_s.Colcount:=m+1;
c_s.Rowcount:=n+1;
tabliza.Rowcount:=n+1;
for i:=1 to n do
begin
form1.tabliza.Cells[0,i]:='B'+intToStr(i);
form1.C_S.Cells[0,i]:='B'+intToStr(i);
for j:=1 to m do
begin
form1.C_S.Cells[j,0]:='A'+intToStr(j);
form1.C_S.Cells[j,i]:=intToStr(C_B[i,j]);
end;
end;
label23.caption:='B';
tabliza.cells[1,0]:='b_малая';tabliza.cells[2,0]:='b_большая';
for j:=1 to n do
begin
tabliza.cells[1,j]:=intToStr(b_m[j]);
tabliza.cells[2,j]:=intToStr(b_b[j]);
end;
for i:=1 to n do
for j:=1 to k do
tabliza.cells[j+2,i]:=floatToStr(V_b[i,j]);
end;
end;
end.
unit Unit2;
interface
uses
Windows, Messages, SysUtils, Classes, Graphics, Controls, Forms, Dialogs,
Grids, StdCtrls, ExtCtrls, Buttons, Menus;
type
TForm2 = class(TForm)
alpfa: TStringGrid;
Panel1: TPanel;
BitBtn1: TBitBtn;
BitBtn2: TBitBtn;
procedure FormShow(Sender: TObject);
procedure BitBtn2Click(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form2: TForm2;
i,j:integer;
implementation
uses osnowa;
{$R *.DFM}
{ Ввод козффициентов оптимизмов}
procedure TForm2.FormShow(Sender: TObject);
begin
j:=0;
form1.tabliza.Visible:=true;
alpfa.Colcount:=strToInt(form1.edit3.text);
for i:=0 to alpfa.Colcount do
begin
j:=j+1;
alpfa.Cells[i,0]:='Alpha'+intToStr(i+1);
alpfa.Cells[i,1]:=FloatToStr(al[j]);
end;
end;
procedure TForm2.BitBtn2Click(Sender: TObject);
begin
j:=0;
for i:=0 to alpfa.Colcount do
begin
j:=j+1;
try
al[j]:=strToFloat(trim(alpfa.Cells[i,1]));
form1.tabliza.Cells[3+i,0]:=alpfa.Cells[i,1];
except
showMessage('Ошибочная запись числа : '+alpfa.Cells[i,1]);
end; end;
end;
end.
 Приложение 2 Результат работы программы
Приложение 2 Результат работы программы
СОДЕРЖАНИЕ
ВВЕДЕНИЕ.. 2
1... ОБЩАЯ ЧАСТЬ.. 3
1.1. Цель разработки. 3
1.2. Анализ использования разработки. 3
1.3. Анализ методов решения задачи. 3
1.4. Анализ средств программирования. 4
1.4.1. Обзор средств программирования. 4
1.4.2. Характеристика программного обеспечения. 4
1.4.3. Характеристика ПК. 6
1.4.4. Характеристика языка программирования. 6
2... СПЕЦИАЛЬНАЯ ЧАСТЬ.. 8
2.1. Постановка задачи. 8
2.2. Экономико – математическая модель. 12
2.3. Описания метода Гурвица. 13
2.4. Алгоритм задачи. 14
2.4.1. Алгоритм основной программы.. 14
2.4.2. Алгоритм процедуры W_rezultat 15
2.5. Описание алгоритма. 21
2.5.1. Описание алгоритма основной программы.. 21
2.5.2. Описания основной процедуры W_rezultat расчета по методу Гурвица 21
2.6. Характеристика программы.. 24
2.7. Описание процесса отладки. 24
2.8. Результаты решения задачи. 25
2.9. Оценки результатов решения задачи. 27
ЗАКЛЮЧЕНИЕ.. 28
СПИСОК ЛИТЕРАТУРЫ... 29
Приложение 1 Текст программы.. 30
Приложение 2. Результаты работы программы.. 36
ВВЕДЕНИЕ
В курсовом проекте представлена задача теория игр.
Одним из разделов теории игр являются состязательные задачи в условиях неопределённости. Состязательные задачи – это задачи, в которых сталкиваются интересы 2-х или более сторон, преследующих различные цели. Для решения этих задач используется методы теории игр. Для состязательных задач в условиях неопределённости в теории игр разработаны соответствующие принципы, на основании которых неопределенные ситуации преобразуется в детерминированные и решаются методом максимина.
Согласно принципу Гурвица неразумно, приняв во внимание самый маленький выигрыш, не учитывать самый большой, для чего необходимо ввести коэффициенты оптимизма (он выполняет роль вероятности). Значения оптимизма выбирают на основании субъективных соображений. В технических приложениях сложно выбрать коэффициент оптимизма, т.к. трудно найти количественную характеристику для тех долей оптимизма и пессимизма, которые присутствуют при принятии решения. Принцип Гурвица учитывает как пессимистический, так и оптимистический подход к ситуации.
ОБЩАЯ ЧАСТЬ
Цель разработки
Данный курсовой проект разрабатывался с целью вывести ситуацию из условия неопределённости; найти максимальный выигрыш, по которому определить оптимальную стратегию каждого игрока и игрока разрешающего конфликтную ситуацию.
Анализ использования разработки
Данный курсовой проект предназначен для прогнозирования в учебных заведениях
Дата: 2019-07-24, просмотров: 268.