В настоящее время наиболее распространенными алгоритмическими языками является Паскаль, Си.
Язык Паскаль был разработан в конце 80-х гадах профессором Н. Виртом. Своё название получил в честь французского математика и философа Б. Паскаля. Язык был создан специально для обучения программированию.
Последняя версия Object Pascal позволила объединить в рамкак единой системы мощный алгоритмический потенциал языка, методы объектно-ориентированного программирования, современную графику, удобные средства тестирования и отладки программы, а также обеспечить дружественный интерфейс с пользователем.
Основные операторы языка являются хорошей иллюстрацией базовый управляющий конструкций структурного программирования.
Большую помощь программистам оказывает библиотека стандартных подпрограмм Паскаля. Эта библиотека модернизируется и пополняется уже более десяти лет, В нее входят средства для работы с оперативной и внешней памятью, клавиатурой, дисплеем и другими внешними устройствами ПЭВМ.
Графический пакет системы программирования Delphi - один из самый мощных пакетов такого типа, т.к. позволяет использовать все функции граф. библиотек OpenGL и Direct3D.
Система программирования Delphi работает по модульному принципу программирования, который лежит в основе всех современных технологий разработки программ, Программа, написанная на Delphi разбита на модули, а те, в свою очередь, состоят из подпрограмм.
Среда в системе программирования Delphi многооконная, на экране дисплея одновременно присутствуют несколько окон редактирования, панель компонент, инспектор объектов, редакторы форм и т, д.
СПЕЦИАЛЬНАЯ ЧАСТЬ
Постановка задачи
Теория игр – теория математических модулей, интересы участников которых различны, причём они достигают своих целей различными путями.
Столкновение противоположных интересов участников приводит к возникновению конфликтных ситуаций. Чтобы исключить трудности, возникающие при анализе конфликтных ситуаций, строится упрощенная модель ситуаций. Такая модель называется игрой. Теория игр относится к теории статистических решений.
В задачах теории игр предполагалось, что в них примут участие две стороны, интересы которых противоположны. Поэтому действия каждой стороны направлены на увеличения выигрыша. Но во многих задачах, приводящих к игровым, неопределенность вызвана отсутствием информации об условиях, в которых осуществляется действие. Эти условия зависят не от сознательных действий другого игрока, а от объективной действительности, которую принято называть природой.
Игру с природой описывается с помощью платёжной матрицы, в которой в качестве игрока А выступает статистик (человек, который принимает решения), имеющий m возможных стратегий А1, А2, …, Аm, а в качестве второго игрока выступает природа.
План, по которому игрок совершает выбор в каждой возможной ситуации и при каждой возможной фактической информации называется стратегий игрока.
Главным в исследовании теории игр является выбор оптимальных стратегий игроков. Стратегия игрока является оптимальной, если применение этой стратегии обеспечит ему наибольший гарантированный выигрыш при всевозможных стратегиях другого игрока. В процессе одной игры каждый из игроков выбирает одну стратеги. Стратегии делятся на чистые и смешанные.
Чистая стратегия – это стратегия, имеющая одно единственное значение или решение из множества заданных.
Смешанная (сложная) стратегия – это стратегия, которая берёт m значений с соответствующими вероятностями.
Стороны участвующие в конфликтной ситуации называются игроками, а предполагаемые действия каждого из игроков, направленные на достижение некоторой цели, называется правилами игры.
Платёж – это количественная оценка результатов игры.
Ходом в теории игр называется выбор одного из предложенных правилами игры действий его осуществлении.
Состязательная задача – это задача, разрешающая конфликтные ситуации между двумя или более противниками с целью нахождения оптимальной стратегии для каждого игрока, и в конечном итоге игрока, разрешающего конфликтную ситуацию.
Игру двух игроков можно описать как производственный процесс с помощью следующей функциональной схемы (рис.1).
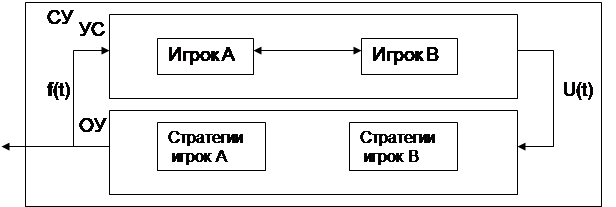 Рисунок 2.1.1
Рисунок 2.1.1
Оба игрока по прямой связи U(t) делает ход, выбирая предполагаемую стратегию. Ни один из игроков не знает хода противника. В случае если игрок узнает стратегию своего противника, то по обратной связи f(t) поступает сигнал, что он может отказаться от своей старой стратегии и выбрать другую стратегию. Востановив работу по прямой связи U(t).
Человек А в играх с природой старается действовать осмотрительно, используя, например, минимаксную стратегию, позволяющую получить наименьший проигрыш. Второй игрок В (природа) действует совершенно случайно, возможные стратегии определяются как её состояние. Условия игры задаются в виде матрицы.
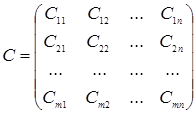
Элементы Сij = выигрышу игрока А, если он использует стратегию Аi.
В данном курсовом проекте состязательная задача решается по методу Гурвица.
Пусть в игре принимают участие два игрока А и В.
Рассматривается конфликтная ситуация между двумя сторонами А и В. Игрок А имеет m стратегий, а В имеет n стратегий: А={А1, А1,…, А1}; В={В1, В1,…, В1}.
Взаимосвязь между стратегиями любого из игроков определяется платёжной матрицей С={Cij}m*n. Cij – выигрыш игрока А. Заданы статистические коэффициенты оптимизации ( 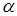 ).
).
Цель игры состоит в том, чтобы вывести ситуацию из условия неопределённости, найти максимальный выигрыш, по которому определить оптимальную стратегию каждого игрока, а также игрока разрешающего конфликтную ситуацию.
Решение игры и исходные данные сводятся в таблицу Гурвица (табл. 2.1.1).
Таблица 2.1.1
|
| В1 | В2 | … | Вn | Наименьший выигрыш | Наибольший выигрыш | Коэффициенты оптимизма | ||
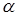 1 1
| … | 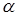 k k
| |||||||
| А1 | C11 | C12 | … | C1n | a1 | А`1 | V11 | … | V1k |
| А2 | C21 | C22 | … | C2n | a 2 | А`2 | V21 | … | V2k |
| … | … | … | … | … | … | … | … | … | … |
| Аm | Cm1 | Cm2 | … | Cmn | a m | А`m | Vm1 | … | Vmk |
Где 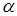 j – статистические коэффициенты оптимизации;
j – статистические коэффициенты оптимизации;
к – количество оптимизмов;
Аj – стратегии игрока А;
Вj - стратегии игрока В;
Vij – расчетные условные выигрыши;
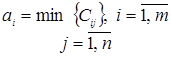
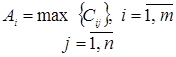
С учётом коэффициентом оптимизма вычисляем условные выигрыши
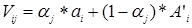
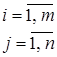
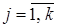
Выбираем решение о выборе стратегии, при 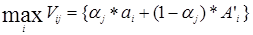 , где 0
, где 0 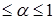 (для
(для 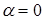 игрок переходит к стратегии «азартного игрока»; для
игрок переходит к стратегии «азартного игрока»; для 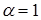 - стратегия абсолютного оптимизма).
- стратегия абсолютного оптимизма).
.
Дата: 2019-07-24, просмотров: 256.