Во множестве целых чисел выполняются операции сложения, вычитания и умножения, но не всегда выполняется операция деления. Расширяя множество Z так, чтобы эта операция была выполнима, получаем новое числовое множество - множество рациональных чисел Q, т.е. Q={r | r= 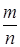 , m, n Î Z, n ¹ 0}. Множество рациональных чисел можно еще определить как множество бесконечных периодических десятичных дробей.
, m, n Î Z, n ¹ 0}. Множество рациональных чисел можно еще определить как множество бесконечных периодических десятичных дробей.

| Десятичная дробь 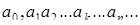 называется периодической, если начиная с некоторого k одна или несколько цифр (группа цифр) повторяются. называется периодической, если начиная с некоторого k одна или несколько цифр (группа цифр) повторяются.
|
Если же число нельзя представить в виде отношения двух целых чисел, то его называют иррациональным числом.
К необходимости введения понятия иррационального числа приводит рассмотрение многих задач, в частности - задачи измерения некоторых отрезков (например, длины диагонали квадрата со стороной, равной единице). Иррациональное число представляется непериодической бесконечной десятичной дробью. Например, рациональные числа 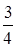 и
и 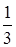 представляются следующими десятичными дробями:
представляются следующими десятичными дробями: 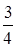 = 0,75;
= 0,75; 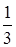 = 0,333 ... = 0,(3).
= 0,333 ... = 0,(3).
Иррациональные числа 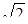 и p представляются непериодическими бесконечными дробями:
и p представляются непериодическими бесконечными дробями: 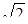 = 1,414...; p = 3,14159....
= 1,414...; p = 3,14159....

| Непериодическими бесконечными дробями также являются:
0,101001000100001..., 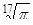 и другие. и другие.
|
Множество, состоящее из всех рациональных и всех иррациональных чисел, называется множеством действительных чисел R. Геометрически действительные числа изображаются точками числовой прямой. Отметим, что между множеством действительных чисел и множеством точек числовой прямой установлено взаимно однозначное соответствие.

| Имеется в виду что каждой точке на прямой соответствует число из множества R, и наоборот, каждому числу из множества R соответствует точка на прямой. |
Система комплексных чисел
Однако действительных чисел недостаточно для того, чтобы решить любое квадратное уравнение с действительными коэффициентами. Например, уравнение вида х2 + 1= 0 действительных корней не имеет. А это означает, что система действительных чисел нуждается в расширении.
О п р е д е л е н и е. Множество чисел вида а + bi, а, b Î R, i2 = - 1, называется системой комплексных чисел С.

| Подчеркнем, что в отличие от множества действительных чисел (R), множество комплексных чисел (С) с операциями определенными на нем не обладает свойством упорядоченности, так как имеется элемент 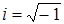 , в частности, нельзя определить понятие быть положительным. , в частности, нельзя определить понятие быть положительным.
|
а - действительная часть комплексного числа, bi - мнимая часть комплексного числа, i = 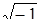 - мнимая единица, b - коэффициент при мнимой единице. Запись числа в виде z = а + bi называется алгебраической. Комплексное число z = а + bi равно нулю тогда и только тогда, когда а = 0 и b = 0. Два комплексных числа z1 = а 1 + b1i и z2 = а 2 + b2i называются равными, если а 1 = a2, и b1 = b2, в этом случае пишут: z1 = z2.
- мнимая единица, b - коэффициент при мнимой единице. Запись числа в виде z = а + bi называется алгебраической. Комплексное число z = а + bi равно нулю тогда и только тогда, когда а = 0 и b = 0. Два комплексных числа z1 = а 1 + b1i и z2 = а 2 + b2i называются равными, если а 1 = a2, и b1 = b2, в этом случае пишут: z1 = z2.
Число 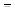 = а - bi называется сопряженным для числа z = а + bi, при этом числа z и
= а - bi называется сопряженным для числа z = а + bi, при этом числа z и 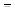 называются взаимно сопряженными. Например, числа z = 2 + i и z = 2 - i; z = -5 - i и z = -5 + i, z = i и z = -i будут взаимно сопряженными.
называются взаимно сопряженными. Например, числа z = 2 + i и z = 2 - i; z = -5 - i и z = -5 + i, z = i и z = -i будут взаимно сопряженными.
Арифметические действия над комплексными числами проводятся по следующим правилам. Пусть z1= а 1 +b1i z2= а 2 + b2i. Тогда: 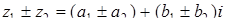 ;
; 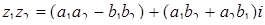 ;
;
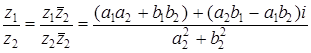 . Таким образом, видим, что если z= a+bi и
. Таким образом, видим, что если z= a+bi и 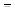 =a-bi, то z
=a-bi, то z 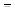 = a2+b2.
= a2+b2.
П р и м е р ы. Выполнить действия:
1. (2 + 3i) + (8 - 5i) = 10 - 2i.
2. (-1 - i) - (2 + 3i) = -3 - 4i.
3. (10 - i)(2 + i) = 21+8i.
4. 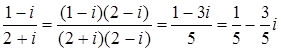 .
.
Геометрически комплексные числа можно изображать точками плоскости, абсциссами которых служат действительные части, а ординатами - коэффициенты при мнимой единице. Таким образом, если z= a+bi, то на плоскости ХОУ это будет точка М(а, b). Так как любой вектор плоскости с началом в точке O(0,0) определяется координатами конца, то комплексные числа также изображают радиус – векторами (рис. 1).
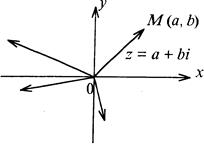
Рис. 1
Кроме алгебраической формы комплексное число может быть записано с помощью тригонометрической формы. Введем следующие определения.
О п р е д е л е н и е. Модулем комплексного числа z = а+ b i называется арифметический квадратный корень из суммы квадратов его действительной части и коэффициента при мнимой единице: |z| = r = 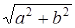 .
.
О п р е д е л е н и е. Аргументом комплексного числа z = а + bi называется число 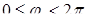 , для которого
, для которого 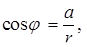
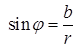 .
.
Возьмем на плоскости точку М(а, b ), пусть ей соответствует комплексное число z = а + bi. Обозначим через j угол, который образует радиус – вектор ОМ с положительным направлением оси ОХ.
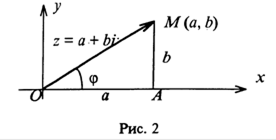
Из D ОМА (рис.2) AO = OMcosj, AM = ОМsinj, но ОМ= 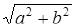 = г, ОА =а; AM =b; тогда z = а + bi = rcos j + ir sin j = r(cos j + isin j ).
= г, ОА =а; AM =b; тогда z = а + bi = rcos j + ir sin j = r(cos j + isin j ).
Запись числа z = r(cos j + isin j ) называется тригонометрической формой комплексного числа.
С геометрической точки зрения, модуль комплексного числа представляет собой длину радиус-вектора, который это число изображает, а аргумент - это угол, который образует данный радиус-вектор с положительным направлением оси ОХ.
П р и м е р. Найти модуль, аргумент и записать число z = 1- i в тригонометрической форме.
Имеем r = 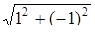 =
= 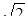 ; cosj =
; cosj = 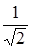 ; sinj =
; sinj = 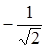 ; тогда j =
; тогда j = 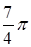 и
и 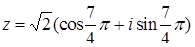 .
.
Используя тригонометрическую форму комплексного числа, умножение и деление комплексных чисел можно выполнять так: если 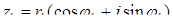 ,
, 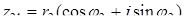 , то z1z2 = r1r2[cos ( j 1 + j 2 ) + isin ( j 1 + j 2 )],
, то z1z2 = r1r2[cos ( j 1 + j 2 ) + isin ( j 1 + j 2 )], 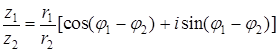 .
.
Операции же возведения в целую степень и извлечения корня удобнее проводить в тригонометрической форме. Так, для возведения в целую степень n комплексного числа z = r(cosj + isinj ) известна формула Муавра:
zn = rn(cos n j + isin n j ).

| Отметим, что возведение комплексных чисел в натуральную степень можно выполнять и в алгебраической форме, просто перемножая число само на себя или воспользовавшись биномом Ньютона. |
П р и м е р. Найти (2 + 2i)5.
Если z = 2 +2i, то r = 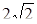 , cosj =
, cosj = 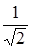 , sinj =
, sinj = 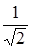 , j =
, j = 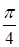 . Тогда
. Тогда
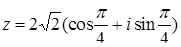 , а
, а 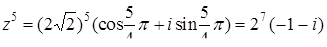 .
.
Для извлечения корня степени n Î N из комплексного числа z = =r(cos j + isin j ) используется следующая формула:
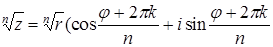 , k = 0, 1, 2, ..., n-1.
, k = 0, 1, 2, ..., n-1.
П р и м e p. Найти 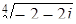 . Найдем тригонометрическую форму подкоренного выражения:
. Найдем тригонометрическую форму подкоренного выражения:
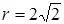 ;
; 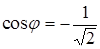 ;
; 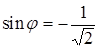 ;
; 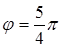 ;
; 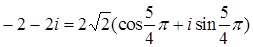 .
.
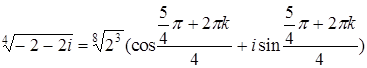 , k = 0, 1, 2, 3.
, k = 0, 1, 2, 3.
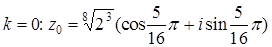 ;
;
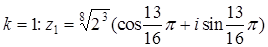 ;
;
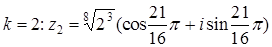 ;
;
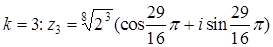 .
.
Контрольные вопросы
После ознакомления с теоретическим материалом студентам предлагается ответить на несколько вопросов по данной теме. Это делается с целью закрепления нового материала и контроля его усвояемости. Форма ввода ответа на вопросы предполагает использование как классической кроудеровской системы, так и возможность ввода конструированного ответа, когда студент конструирует свой ответ из предложенных фрагментов. Система вопросов подбиралась с учетом следующих требований:
– широкий охват нового теоретического материала;
– разноплановость в смысле возможных вариантов ответов;
– отсутствие вопросов предполагающих ответы типа «да» – «нет» и ответов требующих пояснения.
Блок ответов на контрольные вопросы устроен таким образом, что дав ответ на первый вопрос, студенты могут перейти к последнему, затем вернуться назад и исправить первый ответ. Ответ, данный на вопрос, не исчезает, он остается доступным для редактирования и по прошествию некоторого времени. Во время ответа на вопросы доступ к теоретическому материалу не возможен. После получения ответов на все вопросы студентам предлагается закрыть сеанс ответов на вопросы и перейти к решению практических заданий. После этого момента вернуться к вопросам и что-либо исправить уже нельзя. По окончанию сеанса работы с учебником система проанализирует полученные ответы на предмет их правильности и полноты и выставит оценку по пятибальной шкале.
Ниже приводится схема вопросов предлагаемых студентам:
1. Дайте определение числового множества.
2. Какие числовые системы вам известны?
3. Какие принципы лежат в основе расширения числовых множеств?
4. Как определяется множество натуральных чисел?
5. Что собой представляет метод математической индукции?
6. Дайте определение множества целых чисел.
7. Какие основные факты теории целых чисел вам известны?
8. Как определяется множество рациональных чисел?
9. Дайте определение множества действительных чисел.
10. Дайте определение системы комплексных чисел.
11. Какие формы употребляются для записи комплексных чисел?
12. Какова геометрическая интерпретация комплексного числа, его модуля и аргумента?
13. Как умножаются, делятся и возводятся в степень комплексные числа, заданные в тригонометрической форме.
14. Как извлечь корень n-й степени из комплексного числа?
Каждый из вопросов предполагает только один правильный ответ, ответ, не совпадающий с правильным, считается неправильным.
После завершения ответов на вопросы студенты переходят к решению практических заданий.
Практические задания
Целью включения в учебник практических заданий являлось:
– выработка у студентов устойчивых навыков решения подобных заданий;
– закрепление на практике полученных теоретических знаний;
– оценка качества усвоения студентами нового материала;
– повторение и восстановление в памяти ранее изученного материала;
– выработка у студентов навыков компьютерного общения и самостоятельного решения задач в условиях ограниченного времени.
При подборе практических заданий учитывались следующие требования:
– всестороннее отражение в заданиях нового теоретического материала;
– сходность предлагаемых заданий с теми, что рассматривались ранее в виде решенных примеров;
– отсутствие примеров повышенной трудности или требующих нестандартного подхода;
– простота получаемых ответов и удобство их ввода и редактирования.
Ниже приводиться схема предлагаемых практических заданий:
1. По делимому а и остатку r найти делители b и соответствующие частные q, если:
а) a = 100; r = 6; б) а = 158; r = 37; в) a = 497; r = 16.
2. Найти наибольшее целое число, дающее при делении на b = 13 частное q = 17.
3. Найти НОД каждой из следующих систем чисел:
а) (120; 144); б) (424; 477); в) (299; 391; 667).
4. Найти НОК каждой из следующих систем чисел:
а) [120; 96]; б) [75; 114]; в) [118; 177;413].
5. Каким числом, рациональным или иррациональным, является значение выражения 8 - 5х при х = 0,6; 1,2; -3,4?
6.Среди чисел 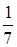 ; 0; 0,(25);
; 0; 0,(25); 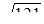 ; 3,14;
; 3,14; 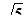 ; 0,818118111811118... укажите рациональные и иррациональные.
; 0,818118111811118... укажите рациональные и иррациональные.
7. Выполнить указанные действия:
а) (2 + 3i) (4 - 5i) + (2 - 3i) (4 + 5i); б) 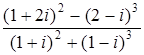 .
.
8. Найти тригонометрическую форму комплексного числа:
а) i; б) -2; в) 1 + i; г) 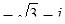 .
.
9. Вычислить:
а) 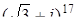 ; б)
; б) 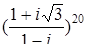 ; в)
; в) 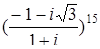 .
.
10. Извлечь корни:
a) 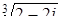 ; б)
; б) 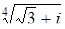 ; в)
; в) 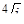 ; г)
; г) 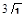 ; д)
; д) 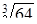 .
.
11. Упростить:
а) 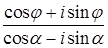 ; б)
; б) 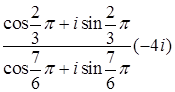 .
.
Предложенные задачи студенты решают у себя в тетради, а потом вводят полученные ответы в компьютер. По окончанию редактирования ответов студенты закрывают сеанс решения практических заданий и система переходит в режим оценки полученных ответов. После анализа выставляется оценка, которая показывается студенту и заносится в ведомость вместе с входными данными студента. Преподаватель, периодически просматривая ведомости (скажем, в конце дня) получает список всех студентов проходивших обучение в этот день и их оценки, может оперативно оценить успешность изложения темы и, если необходимо, принять меры по корректировке учебного процесса.
ЗАКЛЮЧЕНИЕ
В этой дипломной работе рассматривалась тема разработки электронных обучающих систем на примере электронного учебника по математике. Сейчас, когда идет повсеместное внедрение средств новых информационных технологий в высшую школу и образовательный процесс вообще, остро ощущается нехватка программных средств. Для усиления эффективности этого процесса необходимо наличие развитого и многоцелевого программного обеспечения, на основе которого будут строится новые подходы к обучению с применением СНИТ. В этих условиях тема моей дипломной работы, предмет ее исследования представляется очень своевременным. Актуальность этого вопроса продиктована самой ситуацией на рынке программного обеспечения, когда есть люди готовые и стремящиеся внедрять новые программно-методические разработки, новые формы и методы обучения на практике, а несбалансированность российского рынка прикладного обеспечения не позволяет использовать целиком богатый потенциал, заложенный в СНИТ. Поэтому разработку компьютерного учебного пособия по математике, которое могло бы применятся в обучении студентов, считаю своей первостепенной задачей.
В данной дипломной работе передо мной были поставлены следующие цели:
– предоставить студентам, изучающим математику эффективное и легкодоступное средство обучения, которое включало бы в себя теоретический материал, вопросы и практические задания, и выполняло бы не только обучающую, но и контролирующую и оценивающую функции;
– провести анализ теоретического материала предлагаемого к компьютерной реализации с целью определения его пригодности к подобной реализации и степень ее эффективности;
– продолжить, и в чем то оживить, процесс внедрения средств новых информационных технологий в область преподавания математики, ускорить интеграцию математических и информационных дисциплин;
– предоставить нашему университету полноценное программное обеспечение, которое сможет применяться при обучении математике на младших курсах, и которым смогут пользоваться сотни студентов;
Для достижения поставленных целей и решения предложенной задачи мною, была проделана следующая работа:
– рассмотрено современная ситуация в процессе компьютеризации нашего общества и конкретно процесса образования в высшей школе;
– проведена классификация существующих на данный момент компьютерных обучающих систем по их назначению и целям применения в образовании;
– выделены основные условия успешного применения средств НИТ в учебном процессе;
– детально изучена методика создания компьютерных обучающих мультимедиа систем, которая была в дальнейшем использована при разработке собственного компьютерного приложения;
– рассмотрены принципы изложения информации с точки зрения современных теорий психологии и дизайна;
– досконально изучены наиболее популярные инструментальные средства разработки мультимедиа приложений: IBM LinkWay, Action 2.5, Multimedia ToolBook и среда программирования Borland Delphi 3.0;
– проведен сравнительный анализ этих инструментальных сред с целью выявления системы, наиболее отвечающей требованиям, предъявляемым при разработке учебника;
– проведен анализ теоретического материала предлагаемого к изучению студентам I курса отделения «информатика – иностранный язык» и выбран материал для первоочередной реализации в компьютерном учебнике;
– подобрана система контрольных вопросов для выявления уровня усвоения нового материала;
– подобрана система практических заданий предназначенных для закрепления изученного материала и выработке практических умений и навыков в решении подобных заданий;
– разработана система контекстно-вызываемых пояснений, призванная облегчить обучение студентов;
– разработан и реализован действующий фрагмент электронного учебника по математике, который может применяться при обучении студентов;
Практическую ценность своей работы вижу в том, что:
во-первых, мною был получен богатый опыт разработки обучающих компьютерных систем, в том числе освоены инструментальные средства разработки подобных систем;
во-вторых, и это главное, университет получит в свое распоряжение и сможет использовать в образовательном процессе новое электронное средство обучения – компьютерный учебник по математике.
В заключении хочется выразить свою благодарность моим научным руководителям Брановскому Юрию Сергеевичу и Рябогину Анатолию Константиновичу за практическую помощь в работе над электронным учебником и дипломным проектом.
ПРИЛОЖЕНИЕ А:
Дата: 2019-07-24, просмотров: 325.