После анализа нескольких учебников и методических пособий мною был отобран следующий теоретический материал. Совместно с моим научным руководителем Анатолием Константиновичем Рябогиным была разработана система контекстно-зависимых пояснений, которую я также привожу ниже.
 Этим знаком будут обозначаться фрагменты системы подсказок, относящиеся к подчеркнутому слову.
Этим знаком будут обозначаться фрагменты системы подсказок, относящиеся к подчеркнутому слову.
ЧИСЛОВЫЕ СИСТЕМЫ
Множество натуральных чисел
Определение: Множество называется числовым, если его элементами являются числа.
Известны следующие числовые системы:
N - множество натуральных чисел;
Z - множество целых чисел;
Q - множество рациональных чисел;
R - множество действительных чисел;
С - множество комплексных чисел.
Между этими множествами установлены следующие отношения:
N Ì Z Ì Q Ì R Ì C.
В основе расширения числовых множеств лежат следующие принципы: если множество А расширяется до множества В, то:
1) А Ì B;
2) операции и отношения между элементами, выполнимые во множестве А, сохраняются и для элементов множества В;
3) во множестве В выполняются операции, не выполнимые или частично выполнимые во множестве А;
4) множество В является минимальным расширением множества А, обладающим свойствами 1) – 3).

| Минимальность расширения множества А обладающее свойствами 1–3 понимается в том смысле, что: 1. выполняются свойства 1–3; 2. В – наименьшее множество для которого выполняются свойства 1–3 и для которого выполняется операция невыполнимая или частично выполнимая во множестве А. |
Множество натуральных чисел N строго определяется с помощью аксиом Пеано.
1. Существует натуральное число 1, не следующее ни за каким натуральным числом (натуральный ряд начинается с 1).
2. Каждое натуральное число следует только за одним и только одним натуральным числом (в натуральном ряду нет повторений).
3. За каждым натуральным числом следует одно и только одно натуральное число (натуральный ряд бесконечен).
4. Аксиома индукции. Пусть М Ì N. Если:
1) 1 Î М;
2) " а Î М множеству М принадлежит и следующий за а элемент а1 то множество М совпадает с множеством натуральных чисел.
Итак, множество N = { 1, 2, 3, 4,...}.
На аксиоме 4 основан метод математической индукции. Доказательство различных утверждений этим методом проводится от частного к общему, а затем делается вывод о справедливости данного утверждения.
П р и м е р. Доказать методом математической индукции следующее равенство:
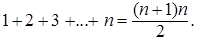
Д о к а з а т е л ь с т в о.
1. Проверим справедливость данного утверждения для n = 1: 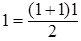 , т.е. 1 = 1.
, т.е. 1 = 1.

| Проверка при n =1 ОБЪЯЗАТЕЛЬНА! |
2. Предположим, что данное равенство выполняется для k слагаемых, т.е. при n =k: 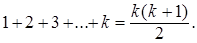
3. На основании предположения 2 докажем справедливость данного равенства для n = k+1:
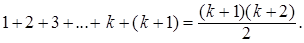
Ho 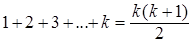 , а потому
, а потому 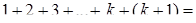
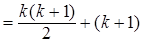 , а так как
, а так как 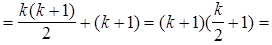
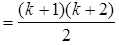 , следовательно
, следовательно 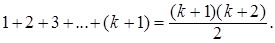
Теперь можно сделать вывод о том, что данное равенство справедливо " n Î N.
Множество целых чисел
Во множестве натуральных чисел выполняются операции сложения и умножения, но не всегда выполняется операция вычитания. Расширяя множество N так, чтобы эта операция была выполнима, мы получаем множество целых чисел Z.

| Расширяя – определяя новую алгебраическую операцию. |
Поэтому Z=N È {0, -1, -2,...} или Z={...-3, -2, -1, 0, 1, 2, 3,...}, т.е. множество целых чисел Z содержит множество натуральных чисел, число нуль и числа, противоположные натуральным.
Основную роль во всей теории целых чисел играют следующие факты.
Т е о р е м а о д е л е н и и с о с т а т к о м. Для любого целого а и b > 0 существуют и притом единственные целые q и r , такие, что а = bq + r, 0 £ r < | b |.
О п р е д е л е н и е. Натуральное число р называется простым, если р > 1 и р не имеет положительных делителей, отличных от 1 и р.
О с н о в н а я т е о р е м а а р и ф м е т и к и. Для каждого натурального числа n > 1 существует единственное разложение на простые множители: 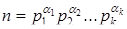 , где p1, p2, ..., pk – простые числа, а
, где p1, p2, ..., pk – простые числа, а 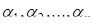 - натуральные числа. Разложение
- натуральные числа. Разложение 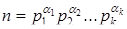 называется каноническим.
называется каноническим.

| Единственность разложения понимается с точностью до порядка следования сомножителей. Например 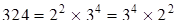 .
Если сказано, что простые числа расположены в порядке возрастания, то данная оговорка не нужна. .
Если сказано, что простые числа расположены в порядке возрастания, то данная оговорка не нужна.
|
О п р е д е л е н и е. 1) Общим делителем целых чисел а 1 , а 2 , ..., а n называется целое число d , такое, что a1 : d, а 2 : d, ... , а n : d. 2) Наибольшим общим делителем целых чисел а 1 , а 2 , ..., а n называется такой положительный общий делитель чисел а 1 , а 2 , ..., а n , который делится на любой другой общий делитель этих чисел.

| Наибольший общий делитель – это наибольший из их общих делителей. |
Обозначается: d = ( а 1 , а 2 , ..., а n ).
Наибольший общий делитель целых чисел а и b может быть найден с помощью алгоритма Евклида, в основе которого лежит теорема о делении с остатком. Последний, отличный от нуля, остаток и будет наибольшим общим делителем чисел а и b.
П р и м е р. Найти НОД чисел 1173 и 323. Последовательным делением находим:
1173 = 323´3 + 204;
323=204´1+119;
204=119´1+85;
119=85´1+34;
85=34´2+17;
34=17´2;
так что (1173, 323) = 17.
О п р е д е л е н и е. Наименьшим общим кратным целых чисел а 1 , а 2 , ..., а n , отличных от нуля, называется наименьшее положительное число, кратное всем этим числам.

| Наименьшее общее кратное – это наименьшее из их общих кратных. |
Обозначают: m=[ а 1 , а 2 , ..., а n].
Пусть а и b целые числа, тогда 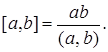
П р и м е р. Найти HOK чисел 1173 и 323.
Т.к. (1173, 323) = 17, то [1173, 323] = 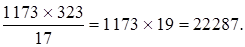
Дата: 2019-07-24, просмотров: 284.