Вот чисто математическая проблема:

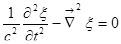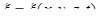уравнение вида , где  – функция координат и времен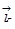и,  и 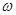 константы, называется волновым уравнением.

Не будем решать уравнение в частных производных, а я сейчас предъявлю одно важное частное решение, и будет доказано, что оно действительно является решением.

Утверждение. Функция вида 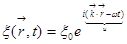 удовлетворяет волновому уравнению (частное решение).

Частное решение, вообще-то, угадывается и проверяется методом тыка. Вот, мы сейчас подставим это решение в уравнение и проверим. Что уравнение утверждает? Что вторая производная по времени от этой функции совпадёт с пространственными производными.

Пишем: , .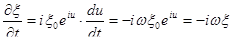

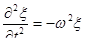Вот чем замечательна комплексная экспонента: можно было бы записать действительные синусы и косинусы, но дифференцировать экспоненты гораздо приятнее, чем синусы и косинусы.

Дальше: .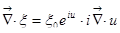

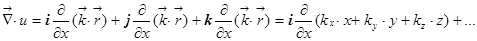
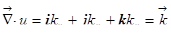, значит, 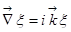. Опять замечательная вещь: оператор  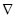действует на функцию 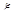, эта функция просто умножается на 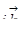, тогда немедленно находим повторное действие оператора1): .

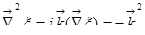Подставим в исходное уравнение: 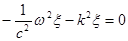, отсюда получаем .

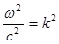Мораль такая: функция вида 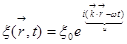 удовлетворяет нашему уравнению, но только при таком условии:

.

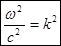Это факт математический. Нам остаётся сообразить теперь, что эта функция изображает.

Если перейти в действительную область, то есть взять сужение этого множества функций на класс действительных функций, это будет решение такого типа: 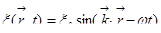. Чтобы не мучиться с тремя переменными, можно это дело упростить: пусть 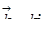, тогда 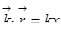. Заметим, что это никакое не ограничение общности, ось х мы всегда можем выбрать вдоль вектора 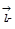. Мы получили функцию от двух переменных: 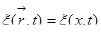. А теперь будем смотреть, что эта функция представляет.

Делаем мгновенную фотографию: фиксируем момент времени 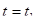 и смотрим пространственную конфигурацию.

Период синуса 2π, ясно, когда х меняется на λ – длину волны (пространственный период), то синус должен измениться на 2π, мы имеем такое соотношение: 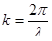. Мы проинтерпретировали константу k – волновое число, а вектор – волновой вектор. Эта мгновенная фотография показывает, как функция зависит от пространства.

Теперь будем следить за временным изменением, то есть сидим в точке х и смотрим, что делается с функцией 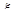 со временем. Фиксируем , тогда 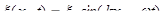, значит, в фиксированной точке опять синусоидальная функция времени. Мы имеем, поскольку период синуса 2π, 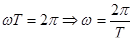, то есть мы проинтерпретировали константу 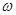,  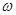называется частотой.

И остаётся, наконец, последнее: запустить обе переменные λ и t, что тогда эта функция будет изображать? Тоже легко понять.

Если 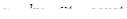, то , а  означает в свою очередь, что 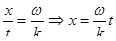. Для событий, для которых координата – линейная функция времени 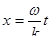, функция всё время одна и та же. Это можно проинтерпретировать так: если мы будем бежать вдоль оси х со скоростью 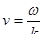, то мы будем всё время видеть перед собой одно и тоже значение этой функции.

Функция, которую мы получили – это синусоидальная волна, бегущая вправо вдоль оси х.

Если мы запустим х и t одновременно, то окажется, что эта синусоида бежит вдоль оси со скоростью 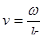, вот такое решение мы получили, ну и тогда понятно, почему это называется волной.

Вот то, что я говорил, что, если мы будем бежать с такой скоростью, мы будем видеть одно и то же значение функции, наглядно:

волны на воде. Для волны на воде – это отклонение волны от горизонтального уровня. Когда вы будете бежать вдоль этой волны со скоростью её распространения, то вы всё время будете видеть перед собой одну и ту же высоту над поверхностью воды.

Другой пример – звуковая волна.

Имеем синусоидальную звуковую волну. Как её создать? Источник колеблется с одной частотой (такой гул на одной частоте мы редко воспринимаем, он, кстати, очень раздражает). Если идёт такая волна определённой тональности, то, когда вы стоите, у вас в ухе давление со временем меняется и создаёт силу, которая давит на перепонку в ухе, колебания перепонки передаются в мозги, с помощью там разных передаточных устройств, и мы будем слышать звук. А что будет, если вы будете бежать вдоль волны со скоростью её распространения? Будет постоянное давление на перепонку и всё, не будет никакого звука. Правда, пример гипотетический, потому что, если в воздухе бежать со скоростью звука, то у вас будет так свистеть в ушах, что вам не будет не до восприятия этой струны.

Волна бежит со скоростью 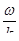, но у нас такое соотношение: 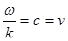. Мы видим, что скорость – это та константа, которая стоит в уравнении.

Решением волнового уравнения является синусоидальная волна, бегущая со скоростью с.

А теперь вернёмся к уравнениям Максвелла. Мы там получили, что 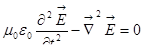. Для магнитного поля аналогично. Такая функция  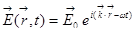удовлетворяет этому уравнению. При условии, что 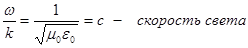. Значит, должны быть электромагнитные волны, распространяющиеся с такой скоростью 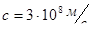. И вот тут уже круг замкнулся. Максвелл получил волновое уравнение и определил скорость волны, а к тому времени было известно экспериментальное значение скорости света, и обнаружилось, что эти скорости равны.

[1] Компьютер так бы и считал: разбивал с заданной точностью кривую на элементы и суммировал. Как завести в компьютер векторное поле? Таблицей: пространство разбиваем на ячейки и заносим значение вектора в каждой ячейке, кривая так же заносится в виде таблицы. В анализе есть способы, как брать такие интегралы, но нас это сейчас не волнует, нам нужно понять смысл.

1) Здесь я ввёл новый математический символ 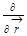 – частная производная, но чтоб не было недоразумений: 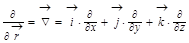. Удобнее писать  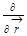вместо 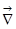, потому что оно прямо содержит в себе указание на то, что нужно делать.

Между прочим, вот, в порядке упражнения полезно было бы для вас вычислить 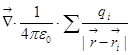, и убедиться, что вы получите предыдущую формулу для напряжённости поля. Это, вот, для самопроверки (не в физике, а в математической квалификации), если вы её получите – это признак того, что вы владеете соответствующим в математике, если нет, –тогда пойдите к своему преподавателю мат. анализа, и пусть он вас там или научит, или накажет.

1) Поле, создаваемое заданным распределением заряда.

2) Любое распределение заряда, рассматриваемое из бесконечности, ну, или издалека, оно всегда ведёт себя как точечный заряд.

3) Интегрирование ведётся по 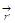, когда по  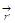интегрирование будет проведено, то эта переменная вылетает вообще, мы получаем число, это  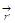сидит здесь как параметр, то есть значение интеграла зависит от 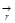, от положения точки, в которой ищется потенциал.

1) Очевидная вещь, что, если мы отойдём достаточно далеко от этого распределения, то какое станет поле? Как от точечного заряда. Значит, на большом расстоянии можно ответ писать сразу: потенциал как от точечного заряда.

2) Это пока точная формула, тут стоит малая величина и квадрат малой величины, вот, если б мы выкинули их, мы получили бы поле точечного заряда, мы же выкинем квадрат малой величины и сделаем формулу более аккуратной.

3) Интегрирование ведётся по штрихованной переменной, по координатам элемента объёма, относительно этого интегрирования .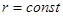

1) 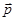- постоянный вектор, характеризующий распределение заряда, постоянная величина.

2) Есть общий рецепт: .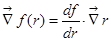

1) То есть мы можем охватить этот заряд замкнутой поверхностью такой, что вне этой поверхности заряда нет.

2) А если кто не знает, тогда пусть себя высечет, потому что должен знать.

1) А дальше мы будем считать, что вектор 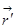 достаточно мал, и эту скалярную функцию мы можем разложить

2) Функцию плотности я переведу в функцию, зависящую от 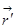,  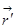задаёт точку однозначно.

1) Там и по другим параметрам может быть разбиение, но здесь на проводники и диэлектрики.

1) Скалярное произведение 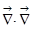это есть 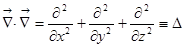. Значит,  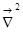обозначается  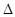и называется оператор Лапласа.

2) Есть целый раздел мат. физики, специально посвящённый решению этого уравнения, и мы обсуждать это не будем.

1) Слово «ёмкость», в общем-то, неудачное, потому что оно наводит на ассоциации бытовые, вроде ёмкость ведра или ёмкость чашки, на самом деле, никакого такого смысла нет. Это я вас просто предупреждаю, потому что часто бывают недоразумения; возникает такое ощущение, что ёмкость проводника связана с зарядом, который можно посадить на этот проводник; на любой проводник можно посадить любой заряд, будет просто различный потенциал при этом, ёмкость будет коэффициентом пропорциональности между потенциалом и зарядом и всё.

1) Вы должны уметь находить ёмкость сферического и цилиндрического конденсаторов.

1) Мы учитываем, что интегрируется по 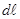 и для всех  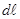другие величины – константы.

1) Интеграл по А D=интегралу по ВС=0, так как 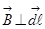, интеграл по CD=0, потому что там  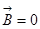по предположению. А на отрезке АВ векторы  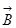и  параллельны.

1) направление нормали задаётся правилом правого винта (обход и нормаль должны образовывать правый винт).

1) Это даже можно сделать. Известно, есть радиактивный распад (когда из ядра вылетают заряженные α-частицы), возьмём шар вот такого радиактивного вещества, из которого вылетают по радиусу α-частицы (это положительно заряженные ядра гелия), эти заряженные частицы представляют вот такой радиальный ток. То есть, эта ситуация реализуема.

1) Физические законы такие вообще, что, когда в них встречается дивергенция какого-то вектора, то у всякого физика непременно возникает желание интегрировать по объёму эту дивергенцию.

1) Имеет место такое математическое тождество 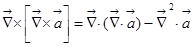. Из первого уравнения 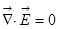, поэтому .

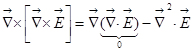1) Воспользуемся формулой 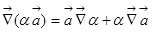 и учтём, что .