Пусть доход от операции Q есть с.в., которую будем обозначать также как и саму операцию Q. Математическое ожидание M[Q]=S(q[i]*p[i]) называют еще средним ожидаемым доходом, а риск операции r = s =ÖD[Q]=Ö(M[Q2]-M2[Q]) отождествляют со средним квадратическим отклонением.
| номер операции | Доходы (Q) и их вероятности (Р) | M[Q] | r | |||
| 1 | 0 | 1 | 5 | 14 | 4,2 | 5,19 |
| 1/5 | 2/5 | 1/5 | 1/5 | |||
| 2 | 2 | 4 | 6 | 18 | 6,8 | 5,74 |
| 1/5 | 2/5 | 1/5 | 1/5 | |||
| 3 | 0 | 8 | 16 | 20 | 8 | 8,72 |
| 1/2 | 1/8 | 1/8 | 1/4 | |||
| 4 | 2 | 12 | 18 | 22 | 16,25 | 6,12 |
| 1/8 | 1/8 | 1/2 | 1/4 | |||
Необходимые расчеты:
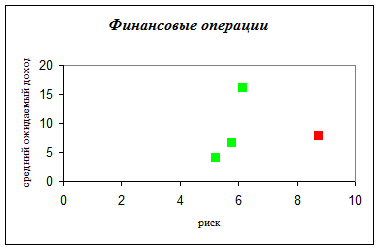
Красным цветом высвечены доминируемые точки (операции), а зеленым – недоминируемые, т.е. оптимальные по Парето. Оптимальными по Парето являются 1-я,2-я и 4-я операции.
Теперь выберем две операции (1-ю: Q1 и 4-ю: Q4), предположим, что они независимы друг от друга и выясним, нет ли операции, являющейся их линейной комбинацией и более хорошей, чем какая-либо из имеющихся.
Пусть Q1 и Q4 две финансовые операции со средним ожидаемым доходом 4,2 и 16,25 и рисками 5,19 и 6,12 соответственно. Пусть t - какое-нибудь число между 0 и 1 . Тогда операция Qt=(1-t)Q1+tQ4 называется линейной комбинацией операций Q1,Q4. Средний ожидаемый доход операции Qt равен M[Qt] = 4,2* (1-t) + 16,25*t, а риск операции Qt равен rt =Ö(26,94*(1-t)2+37,44*t2). Была найдена операция Q*, являющаяся линейной комбинацией исходных операций, со средним ожидаемым доходом 9,14 и риском 3,96, которая превосходит все имеющиеся операции по риску.
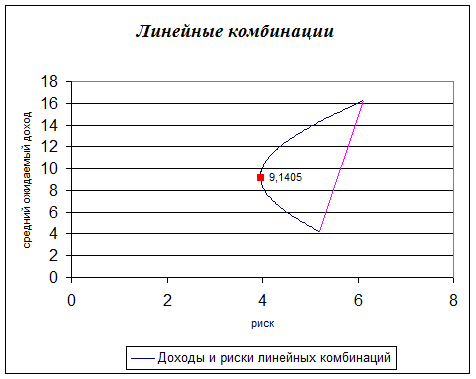
Определить лучшую и худшую операции можно также с помощью взвешивающей формулы f(Q)= 2*M[Q] – r. Имеем: f(Q1)=3,21; f(Q2)=7,86; f(Q3)=7,28; f(Q4)=26,38. Следовательно, 4-я операция является самой лучшей, а 1-я – самой худшей.
Статистический анализ денежных потоков.
Исходные данные для анализа: ежедневные (суммарные) денежные вклады населения в отделение сбербанка в течение 4-х недель (или аналогичный какой-нибудь денежный поток).
Исходные данные:
| 1-я неделя | 2-я неделя | 3-я неделя | 4-я неделя | ||||||||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 1 | 2 | 3 | 4 | 5 | 6 | 1 | 2 | 3 | 4 | 5 | 6 | 1 | 2 | 3 | 4 | 5 | 6 |
| 6 | 5 | 13 | 15 | 14 | 13 | 9 | 9 | 9 | 9 | 9 | 9 | 12 | 12 | 12 | 12 | 12 | 12 | 3 | 1 | 17 | 19 | 5 | 4 |
Денежный поток:
| 6 | 5 | 13 | 15 | 14 | 13 | 9 | 9 | 9 | 9 | 9 | 9 | 12 | 12 | 12 | 12 | 12 | 12 | 3 | 1 | 17 | 19 | 5 | 4 |
Ранжированный ряд:
| 1 | 3 | 4 | 5 | 5 | 6 | 9 | 9 | 9 | 9 | 9 | 9 | 12 | 12 | 12 | 12 | 12 | 12 | 13 | 13 | 14 | 15 | 17 | 19 |
Дискретный вариационный ряд:
| значения | 1 | 3 | 4 | 5 | 6 | 9 | 12 | 13 | 14 | 15 | 17 | 19 |
| частоты | 1 | 1 | 1 | 2 | 1 | 6 | 6 | 2 | 1 | 1 | 1 | 1 |
| частости | 1/24 | 1/24 | 1/24 | 2/24 | 1/24 | 6/24 | 6/24 | 2/24 | 1/24 | 1/24 | 1/24 | 1/24 |
Многоугольник частот:
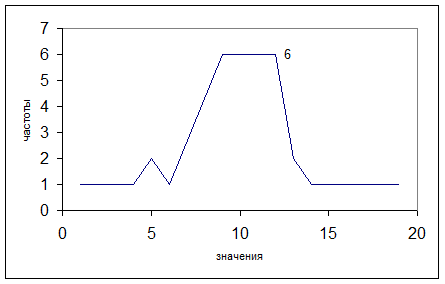
Интервальный вариационный ряд:
| Границы интервалов | 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | |||||||||||
| Середины интервалов | 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | ||||||||||||
| Частоты | 1 | 1 | 3 | 1 | 6 | 0 | 8 | 2 | 1 | 1 | ||||||||||||
| Частости | 1/24 | 1/24 | 3/24 | 1/24 | 6/24 | 1/24 | 8/24 | 2/24 | 1/24 | 1/24 | ||||||||||||
Многоугольник частостей:
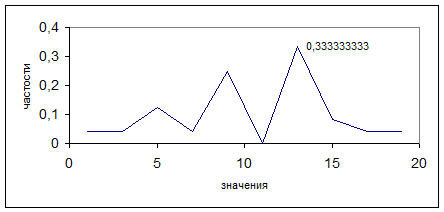
Выборочная функция распределения:
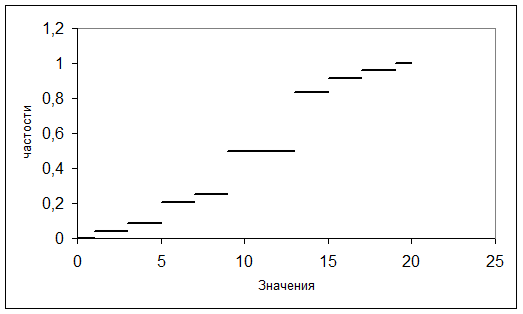
Статистические характеристики:
| По исходному ряду | По дискретному ряду | По интервальному ряду | |
| Выборочная средняя | 10,4 | 10,4 | 10,42 |
| Выборочная дисперсия | 18,79 | 18,79 | 19,88 |
| Выборочное СКО | 4,33 | 4,33 | 4,46 |
| Несмещенная оценка ген. диспер. | 19,61 | 19,61 | 20,75 |
Необходимые формулы и расчеты:
Задача формирования оптимального портфеля ценных бумаг.
Модели сотрудничества и конкуренции.
Дата: 2019-07-24, просмотров: 288.