Предположим, что ЛПР (Лицо, Принимающее Решения) обдумывает четыре возможных решения. Но ситуация на рынке неопределенна, она может быть одной из четырех. С помощью экспертов ЛПР составляет матрицу доходов Q. Элемент этой матрицы q[i,j] показывает доход, полученный ЛПР, если им принято i-е решение, а ситуация оказалась j-я. В этой ситуации полной неопределенности могут быть высказаны лишь некоторые соображения о том, какое решение принять. Сначала построим матрицу рисков. Строится эта матрица так: в каждом столбце матрицы доходов находим максимальный элемент d[j] , после чего элементы r[i,j]=d[j]-q[i,j] и образуют матрицу рисков.
Смысл рисков таков: если бы ЛПР знал что в реальности имеет место j-я ситуация, то он выбрал бы решение с наибольшим доходом, но он не знает, поэтому, принимая i-е решение он рискует недобрать d[j]-q[i,j] - что и есть риск.
матрица доходов
| Варианты (ситуации) | max | min | Вальд | Гурвиц: l*max+ +(1-l)*min; l=1/3 | ||||
| Решения | 0 | 1 | 2 | 8 | 8 | 0 | 2,67 | |
| 2 | 3 | 4 | 10 | 10 | 2 | 2 | 4,67 | |
| 0 | 4 | 6 | 10 | 10 | 0 | 3,32 | ||
| 2 | 6 | 8 | 12 | 12 | 2 | 2 | 5,32 | |
матрица рисков
| Варианты (ситуации) | max | Сэвидж | ||||
| Решения | 2 | 5 | 6 | 4 | 6 | |
| 0 | 3 | 4 | 2 | 4 | ||
| 2 | 2 | 2 | 2 | 2 | ||
| 0 | 0 | 0 | 0 | 0 | 0 | |
Правило Вальда называют правилом крайнего пессимизма: ЛПР уверен, что какое-бы решение он ни принял, ситуация сложится для него самая плохая, так что, принимая i-е решение, он получит минимальный доход q[i]=min{q[i,j]:j=1..4}. Но теперь уже из чисел q[i] ЛПР выбирает максимальное и принимает соответствующее решение.
По правилу Сэвиджа находят в каждой строке матрицы рисков максимальный элемент r[i] и затем из чисел r[i] находят минимальное и принимают соответствующее решение.
По правилу Гурвица для каждой строки матрицы доходов находят величину z[i]=l*max{q[i,j]:j=1..4}+(1-l)*min{q[i,j]:j=1..4}, потом находят из чисел z[i] наибольшее и принимают соответствующее решение. Число l каждый ЛПР выбирает индивидуально - оно отражает его отношение к доходу и риску, при приближении l к 0 правило Гурвица приближается к правилу Вальда, при приближении l к 1 - к правилу розового оптимизма, в нашем случае l равно 1/3.
Итак, по правилу Вальда нам следует принять либо 2-ое, либо 4-ое решение. Сэвидж и Гурвиц нам советуют принять 4-ое решение.
Пусть теперь нам известны вероятности ситуаций - p[j]. Имея матрицу доходов Q теперь можно сказать, что доход от i-го решения есть с.в. Q[i] с доходами q[i,j] и вероятностями этих доходов p[j]. Кроме того, риск i-го решения также есть с.в. R[i] с рисками r[i,j] и вероятностями этих рисков p[j].
Тогда М(Q[i]), М(R[i]) - средний ожидаемый доход и средний ожидаемый риск i-го решения. Принимать решение (проводить операцию) нужно такое, у которого наибольший средний ожидаемый доход, или наименьший средний ожидаемый риск.
| Варианты (ситуации) | М(Q[i]), М(R[i]) | ||||||||
| Доходы | 0 | 1 | 2 | 8 | 2 | ||||
| 2 | 3 | 4 | 10 | 4 | |||||
| 0 | 4 | 6 | 10 | 4 | |||||
| 2 | 6 | 8 | 12 | 6 | |||||
| Риски | 2 | 5 | 6 | 4 | 4 | ||||
| 0 | 3 | 4 | 2 | 2 | |||||
| 2 | 2 | 2 | 2 | 2 | |||||
| 0 | 0 | 0 | 0 | 0 | |||||
| p[j] | 1/3 | 1/3 | 1/6 | 1/6 |
| ||||
М(Q[i])= S (q[i,j]* p[j]) М(R[i])= S (r[i,j]* p[j])
Голубым цветом выделен наибольший средний ожидаемый доход (4-ое решение), а красным цветом – наибольший средний ожидаемый риск (4-ое решение). Как видим, они соответствуют одному и тому же решения. Его и следует принять.
Операции: 1-я – (4;2), 2-я – (2;4), 3-я – (2;4), 4-я – (0;6).
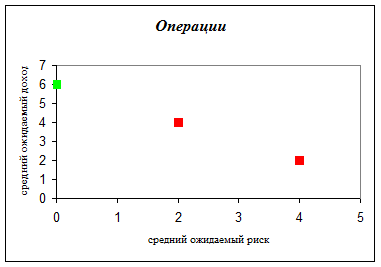
Красным цветом высвечены доминируемые точки (операции), а зеленым – недоминируемые, т.е. оптимальные по Парето. Оптимальной по Парето является 4-я операция.
Была проведена пробная операция, которая значительно сместила распределение вероятностей.
| Варианты (ситуации) | М(Q[i]), М(R[i]) | М*(Q[i]), М*(R[i]) | |||||||
| Доходы | 0 | 1 | 2 | 8 | 2 | 7,2 | |||
| 2 | 3 | 4 | 10 | 4 | 9,2 | ||||
| 0 | 4 | 6 | 10 | 4 | 9 | ||||
| 2 | 6 | 8 | 12 | 6 | 11 | ||||
| Риски | 2 | 5 | 6 | 4 | 4 | 3,8 | |||
| 0 | 3 | 4 | 2 | 2 | 1,8 | ||||
| 2 | 2 | 2 | 2 | 2 | 2 | ||||
| 0 | 0 | 0 | 0 | 0 | 0 | ||||
| p[j] | 1/3 | 1/3 | 1/6 | 1/6 |
| ||||
| p*[j] | 0,1 | 0 | 0 | 0,9 | |||||
Где p*[j] – вероятности после проведения пробной операции. М*(Q[i]), М*(R[i]) – средний ожидаемый доход и риск после проведения пробной операции.
Максимально оправданная стоимость пробной операции равна М*(Q[i]) - М(Q[i])=11 – 6 = 5.
Теперь выберем какие-нибудь две операции (1-ю и 4-ю), предположим, что они независимы друг от друга и найдем операцию, являющуюся их линейной комбинацией и более хорошую, чем какая-либо из имеющихся.
1-я операция = (4,2); 4-я операция = (0,6)
Результат: нельзя подобрать такой операции, являющейся линейной комбинацией 1-ой и 4-ой операции, которая бы доминировала все имеющиеся операции.
Пусть взвешивающая формула f(Q)=М[Q]/M[R], при M[R] не равным нулю, тогда для 1- 4 операций f1=0,5; f2=2; f3=2; f4= ¥. Следовательно 4-я операция является самой лучшей (max=¥), а 1-я – самая худшая.
Дата: 2019-07-24, просмотров: 394.