Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

в крайних децильных группах домашних хозяйств

Потребле-ние кофе за год, кг	В % к итогу по 10%-ным группам домохозяйств		Потребление кофе
	наименее обеспечен-ных F1	наиболее обеспе-ченных F10	в сред­нем по группе П i	общее по децильной группе
				первой C1=ПiF1	десятой C10= ПiF10
Менее 3	38	6	2	76	12
3-5	22	12	4	88	48
5-7	18	34	6	108	204
7-9	14	28	8	112	224
9 и более	8	20	10	80	200
Итого	100	100		464	688
Обследова-но домохо-зяйств	126	132

 

Вычислим показатели потребления по каждой децильной группе:

а) среднее потребление кофе на одно домохозяйство

в первой децильной группе

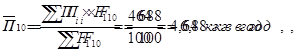в десятой децильной группе

 

б) дисперсию потребления

в первой децильной группе

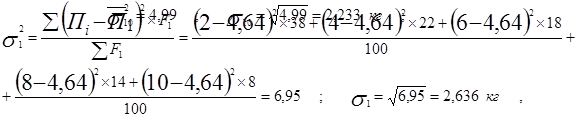      в десятой децильной группе

 

в) коэффициент вариации потребления

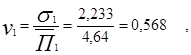в первой децильной группе

т. е. вариация умеренная и по потреблению кофе обследованные домохозяйства первой децильной группы неоднородны,

в десятой децильной группе

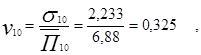вариация потребления кофе в домохозяйствах десятой децильной группы слабая, а потребители достаточно однородны;

г) доля потребляющих кофе от 3 до 7 кг в год

в первой децильной группе w₁ = 22 + 18= 40% = 0,4;

в десятой децильной группе w₁₀ = 12 + 34 = 46% = 0,46.

Оценка значимости показателей потребления производится при небольшом объеме единиц в каждой выделенной группе. В данном примере их применение нецелесообразно, так как в каждой группе обследовано более 100 домохозяйств:

а) для среднего потребления

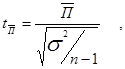      где n — число обследованных хозяйств;

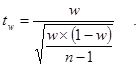б) для доли потребления в определенных границах

Расчетные значения t-критерия Стьюдента сравниваются с табличными (t _табл при уровне значимости a = 0,05 и числе степеней свободы df = n - 2). Анализируемый показатель незначимо отличен от нуля при t _факт < t _табл. В этом случае показатель потребления статистически ненадежен. При t _факт ³ t _табл рассматриваемый по­казатель статистически значимо отличен от нуля и надежен. При получении ненадежных показателей потребления необходимо увеличить число наблюдений или укрупнить выделенные группы (например, перейти от децильных к квинтильным группам).

Проанализируем статистическую оценку существенности различий в показателях потребления в сравниваемых группах. Для сравнения средних долей и коэффициентов вариации при­меняется t-критерий Стьюдента. При этом выдвигается нуль-ги­потеза (Н₀) о несущественных различиях между показателями, вычисленными по децильным группам. При t _факт < t _табл , a = 0,05 и df = n₁ + n₂ - 2 нуль-гипотеза принимается. При t _факт ³ t _табл нуль-гипотеза отвергается, что позволяет считать различия сущест­венными.

Рассмотрим оценки существенности различий в потреблении по данным табл. 6.2. Оценка существенности различий в среднем потреблении кофе

 

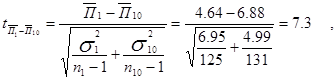Н₀: П₁ » П₁₀ ;

т ак как t _факт > t _табл 1,96 при a= 0,05 и df = n₁ + n₂ - 2 = 126 + 132 – 2 = 256, гипотеза H_о отклоняется. Другими словами, выявлены различия в потреблении кофе в крайних децильных группах домохозяйств, в наиболее обеспеченной группе оно выше.

Оценка существенности различий в вариации потребления кофе

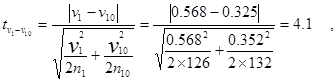Н₀: v ₁ » v ₁₀ ;

так как t _факт > t _табл, то гипотеза Н₀ отклоняется. Выявлены суще­ственные различия в вариации потребления в крайних децильных группах, и в наименее обеспеченной группе потребителей опо-требление более разнообразно.

Оценка существенности различий в долях домохозяйств с оп­ределенным уровнем потребления кофе

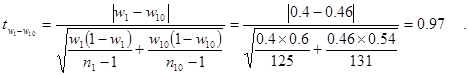Н₀: w ₁ » w ₁₀ ;

Поскольку t _факт < t _табл, то гипотеза Н₀ принимается, т. е. суще­ственных различий в долях домохозяйств с потреблением кофе от 3 до 7 кг в год не выявлено.

Рассмотрим использование критерия Бартлета для проверки гипотезы об однородности дисперсий. Этот критерий считается са­мым мощным. Он позволяет одновременно сравнивать несколько дисперсий, не ограничен попарными сравнениями. Применение критерия Бартлета основано на предположении о нормальности (близости к ней) распределения изучаемого признака в группах, по которым исчислены дисперсии.

При объеме совокупности больше 50 единиц

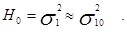Порядок расчета критерия Бартлета следующий:

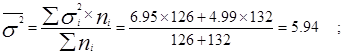а) вычисляется средняя арифметическая из сравниваемых дисперсий

б) находится десятичный логарифм этой величины

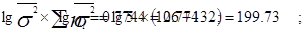в) находится

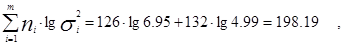г) определяется средняя геометрическая из логарифмов ди­сперсий

где m — число сравниваемых дисперсий;

 

д) критерий Бартлета

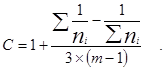Величина М нормируется на величину

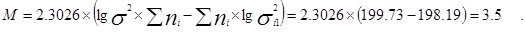Отношение М/С подчиняется распределению ײ с числом степеней свободы df= m -1. При М/С < × ² _табл принимается гипотеза Н₀, т. е. различия между дисперсиями незначимы. При М/С ≥ × ² _табл гипотеза Н₀ отклоняется; между дисперсиями есть существен­ные различия.

В данном случае:

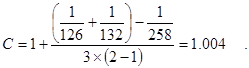M/C = 3.55/1.004 = 3.54 ; × ² _табл = 3.8 ( a = 0,05 ; df = 265)

Здесь М/С < х_табл, гипотеза Н₀ подтверждается, и дисперсии различаются незначимо.

Проведенный анализ оценки существенности различий в пока­зателях потребления кофе в крайних децильных группах выявил существенные различия в уровне и в вариации потребления. Несуще­ственны различия в дисперсиях и по доле потребителей, потребляющих кофе от 3 до 7 кг в год.

Сопоставить распределения по потреблению кофе позво­ляют построение кривой Лоренца и расчет коэффициента Джини (табл. 3).

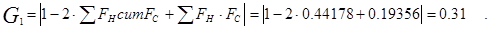Коэффициент Джини

Аналогично по десятой децильной группе коэффициент Джи­ни G₁₀ = 0,132. Сопоставление коэффициентов между собой под­тверждает ранее сделанный вывод, что дифференциация по­требления кофе в наименее обеспеченных домохозяйствах выше, чем среди наиболее обеспеченных. [5]

Таблица З

Результаты расчета коэффициента Джини на примере первой децильной группы домохозяйств (наименее обеспеченных)

Потреб-ление ко-фе в год	Доля домохо-зяйств FH	Общий объем потребления		Накопленная час- тость по объему потребления cumFC	FH·FC	FH cumFC	CumFH
		кг С 1	долей к итогу FC
Менее 3	0.38	76	0.164	0.164	0.06232	0.06232	0.38
3 – 5	0.22	88	0.190	0.354	0.04180	0.07788	0.60
5 – 7	0.18	108	0.233	0.587	0.04194	0.10566	0.78
7 – 9	0.14	112	0.241	0.828	0.03374	0.11592	0.92
9 и более	0.08	80	0.172	1	0.01376	0.08000	1.00
Итого	1	464	1