Примечания О. И. Генисаретского

I. ПРОСТРАНСТВО ЕВКЛИДА

1925. IV. 26

Пространственность, как всегдашняя и необходимая сторона всякого опыта, и переживаемого и мысленного, есть тем самым и наиболее известная нам сторона действительности[181]. И потому обсуждать пространственность в художественном произведении, казалось бы, —самый доступный и самый легкий из моментов художественной критики. Все остальное, будучи частным, требует и соответственных специальных знаний; только пространственность, непосредственно данная произведением, говорит сама за себя и, следовательно, предполагает в критике лишь некоторую внимательность к тому, что он видит и слышит.

Но, как хорошо известно, на деле выходит как раз наоборот. Сюжет, стиль, школа, индивидуальная манера, даже технические приемы произведения, все это, несомненно, требующее особой подготовки, находит себе истолкователей и обсуждается, без вопиющих погрешностей и в пределах известной грамотности, широкими кругами. Между тем именно то, что по природе своей общедоступно, пространственность, она не анализируется и даже непосредственно не воспринимается в подавляющем большинстве случаев, обсуждения же ее, когда возникают, в очень узких кругах, остаются глубоко чуждыми мысли окружающих и даже встречаются ими враждебно.

Непонятность такого положения вещей, впрочем, легко рассеивается: причина его ясна. Это —гипноз отвлеченных понятий о пространстве, внедряемых с молоком матери элементарной геометрией и математическим естествознанием. Приходя в брожение и получая активность от носящихся в воздухе спор кантовской философии, эти понятия отравляют сознание. Создается в нем строгая цензура, возбраняющая выводить из полумрака подсознательного непосредственно воспринимаемую пространственность, в ее подлинном строении, а тем более — говорить о ней вслух. Пространственность произведени нельзя ни видеть, ни слышать и так далее: она говорит сама за себя, «сама собою существует и сама чрез себя понимается — per se est et per se intelligitur». Но, под давлением цензуры, это восприятие выталкивается из сознания, и суждение восприятия подменяется суждением долженствования, строемым на основе вышеуказанных внедренных понятий и схем: видя не видят и слыша не слышат.

Это искажение опыта цензурою тяготеет не только над критиками, не говоря уже о широких кругах, но нередко, в новое время —над самими художниками, которые не позволяют себе выразить ту пространственность, которая на самом деле определяет их образы, но переделывают ее, сколько могут, согласно отвлеченным требованиям. Правда, эта переделка никогда не может быть доведена до конца, потому что тогда образы должны были бы сполна лишиться наглядности, хотя бы даже той, какая свойственна графикам и диаграммам. Но все же, весьма нередко она ведется настолько далеко, чтобы разрушить пространственную цельность всего произведения и сделать его лоскутною сшивкою кусочков, из которых каждый сам по себе все‑таки не подчиняется отвлеченным требованиям, предъявляемым пространственности, и лишь по своей относительной малости контрабандно остается наглядным.

II

Вышеуказанные отвлеченные понятия о пространстве могут быть разделены на два разряда: один из них относится к пониманию самого пространства, как реальности, подлежащей изображению, а другой —к способу и законам этой передачи. Исторически первый разряд понятий может быть охарактеризован как не отчетливо продуманная теория евклидо–кантовского пространства, а второй — как тоже смутно сознаваемая в своих предпосылках и следствиях теория перспективы.

В этих ближайших параграфах нам предстоит собственно обсудить понимание самого пространства.

Само собою разумеется, не может быть никакой речи о ложности понимания пространства по Евклиду и Канту: ведь здесь строится на основании определенных предпосылок стройная схема, но вполне отвлеченная и стараниями соисследователей на протяжении веков, особенно последнего времени, всеми силами стремящаяся очиститься от последних следов наглядности. Теория канто–евклидовского пространства всю свою честь полагает в полной обособленности от конкретного и наглядного миро–восприятия, и именно сюда, т. е. к этому окончательному обособлению, направлены ее напряженные усилия. Ее задача быть хотя и человеком построенной, но насквозь и начисто без–человечной, свободной от малейшего признака антропоцентричности. Между тем задача искусства, всякого искусства во всех его отраслях, именно человечность, подлинное и беспримесное выражение живого человеческого опыта. Искусство всю свою честь видит в наглядности, т. е. подлинной переживаемое™, своих образов: все, что примышлено к наглядному от отвлеченной мысли и тем самым не имеет центром самого человека, это есть фальсификация художественного творчества. Итак, отвлеченное геометрическое построение канто–евклидовского пространства в геометрии и наглядное построение живого пространства в художестве расходятся в самых своих задачах. Не художнику или художественному критику упрекать первое в ложности, но и не строителю отвлеченного пространства вносить поправки в пространственность художественных произведений, после того как он принципиально отстранился от пространственной наглядности. Геометр и художник имеют дело с пространством совершенно в разных смыслах, и линиям их движений не было бы поводов пересекаться, если бы не непрошеное посредничество критиков, которые, не зная и не понимая задач геометрии, берут на себя представительство за нее в художестве, им тоже чуждом, и силятся здесь законодательствовать.

Иначе говоря, в наших рассуждениях речь может идти не о геометрии и вообще не об отвлеченном пространстве, а лишь об уместности применения тех или иных отвлеченных схем к данным наглядным образам.

III

Хотя существенное различие пространства отвлеченного и пространства наглядного должно быть очевидно, поскольку оно предрешено самыми задачами отвлеченной геометрической мысли и художественного творчества, тем не менее отвлеченные понятия настолько деспотически направляют всякий художественный анализ и даже самое творчество в свою сторону, что психологически полезно убедиться на обсуждении отдельных признаков отвлеченного пространства в его далекости от пространства наглядно воспринимаемого и даже в полном их несходстве.

Евклидовско–кантовское пространство характеризуется прежде всего нижеследующими признаками:

оно бесконечно;

оно беспредельно;

оно однородно;

оно изотропно;

оно связно;

оно однозначно;

оно трехмерно;

оно имеет постоянную кривизну, равную нулю.

Сюда можно было бы присоединить и еще некоторые признаки, наличием которых дается право считать пространство удовлетворяющим евклидо–кантовской схеме; но остановимся пока лишь на перечисленных и бегло просмотрим их ряд, с тем чтобы сопоставить далее эти признаки с таковыми же пространства или, точнее, пространств наглядного созерцания в опыте.

1[182]. Пространство бесконечно. Это значит, геометрические количества каждого рода, характеризующие геометрические образы, всегда могут быть доводимы до значений, превосходящих всякую данную величину, или, точнее сказать, всякую мысленно взятую величину. Каким бы числом мы ни охарактеризовали объем, площадь или длину, всегда может быть указан в пространстве геометрический образ, объем которого, площадь поверхности и длина прямолинейных отрезков, в нем заключенных, превосходит в своем численном выражении вышеуказанные. Известным постулатом Архимеда утверждается, что всякая длина прямолинейного отрезка может быть превзойдена, если взять некоторое, достаточно большое, но всегда конечное число раз некоторый отрезок, как бы он ни был короток. В данном случае постулат Архимеда берется навыворот: как бы велик ни был некоторый отрезок и какое бы большое число раз он ни был повторен, всегда может быть взят отрезок более длинный, нежели полученный вышеуказанным приемом сложения. И то же самое должно быть повторено о площадях и объемах. — Можно пояснить ту же мысль еще иначе: взяв любую единицу длины, площади или объема, можно приставить к ней какой угодно большой коэффициент, и суждение о геометрической возможности соответственного образа всегда будет справедливым.

2. Пространство беспредельно. От утверждения бесконечности пространства должно быть отличаемо утверждение его беспредельности. Под беспредельностью разумеется свойство пространства никогда не задерживать поступательного движения по прямой, и притом — произвольно взятой прямой, так что со стороны пространства предела движению, в смысле необходимости остановки, оказано никогда не может быть. Поступательное движение, если оно вынуждено прекратиться, терпит это от действия сил или от материальных препятствий, но никак не от пространства. Ясное дело, беспредельность пространства не предполагает непременно бесконечности его, как и, наоборот, бесконечность не включает в себя непременно беспредельности. Всякое смыкание в себя геометрических образов, если они принимаются за основные, устанавливает и возможность беспредельного движения по ним, хотя образы эти конечны. И наоборот, из возможности брать в пространстве величины, превосходящие всякую данную того же рода, вовсе не следует, что никакое движение не может быть остановлено в силу строения самого пространства. Живя на геоиде и принимая за кратчайшие, т. е. за прямые, или скорее прямейшие, линии его геодезические, мы встречаем в своем движении по геодезическим линиям лишь материальные препятствия, и со стороны чисто геометрической геоид должен считаться двухмерным пространством беспредельным; однако это не мешает быть ему конечным.

3. Пространство однородно. Где бы мы ни вырезали мысленно кусок пространства, все геометрические свойства его будут совершенно тождественными со свойствами куска из другого места. Это можно выразить еще, сказав, что место в отношении свойств и характеристик геометрических образов не имеет никакого значения. Любое геометрическое построение, сколь угодно большое и сколь угодно малое, может быть перемещено в пространстве куда угодно, и никаких последствий этого перемещения внутри самого образа наблюдено не будет. Противоположною этой однородности была бы неоднородность пространства, которую можно мыслить двояко:

либо как постепенное изменение свойств пространства, а следовательно, и образов, в нем содержащихся, в зависимости от места, наподобие воздуха все менее плотного по мере удаления от земли,

либо как зернистость пространства[183], в силу которой свойства больших образов могут быть всюду одинаковыми, но свойства достаточно малых различны в зависимости от зерна или области той или другой природы, в которую данный образ попадет,

либо, наконец, как сочетание того и другого. В первом случае, небольшие сдвиги не изменяли бы существенно пространственных характеристик образов, но большие — вели бы к этому. Во втором случае, и большие, и малые смещения больших образов были бы безразличны, но достаточно малые образы прерывно меняли бы свои характеристики и, при малых сдвигах, внезапно попадали в новые пространственные области. Наконец, третий случай давал бы изменения двоякие. Утверждением однородности пространства исключаются все три случая.

4[184]. Пространство изотропно. Понятие об изотропности сопряжено с понятием об однородности, подобно тому как в проективной геометрии двойственно сопряжены прямая и точка. Тут даже не только подобие обоих отношений, но и связь более существенная: однородность характеризует пространство в каждой его точке, а изотропность — в каждом его направлении. Если мы переходим в пространстве от одной точки к другой, то, вообще говоря, нет никаких оснований ждать полной тождественности имеющихся в них свойств его; а если таковая все‑таки окажется, то данное пространство должно рассматриваться как некоторый весьма специальный случай. Но если бы этот специальный случай и имел место, то остается еще полная возможность встретить разные свойства пространства, в зависимости от направления проведенного в нем прямолинейного луча. Все параллельные между собою прямые дадут одну и ту же характеристику пространства. Новая же система параллелей охарактеризует пространство по–иному. Иначе говоря, пространство, хотя бы и вполне однородное, может быть подобным кристаллической среде, т. е. быть анизотропным. Требуется доказать в каждом данном случае независимость свойств пространства от направления в нем, чтобы иметь право называть данное пространство изотропным. — Как было только что указано, безразличие места в пространстве, т. е. свойства пространства быть однородным, еще ничего не предрешает в вопросе о безразличии направления в нем, т. е. его свойства быть изотропным. Но и наоборот, пространство изотропное может и не быть однородным. Так, пространство с неоднородностями, распределенными вполне беспорядочно, будет вполне изотропно, но однородным не будет.

Таким образом, изотропность и однородность пространства—признаки друг от друга независимые, и совмещение их есть очень специальный случай, который подлежит особому доказательству.

5. Но, кроме изотропности, должно быть особо утверждаемо свойство, которое формально можно было бы подвести под понятие изотропности, но по своему внутреннему смыслу, ради отчетливости, должно рассматриваться как самостоятельное. Это свойство — битлярностъ. В самом деле, у прямой линии, кроме ее направления (direction), должен рассматриваться ее смысл (sens), и требуется всякий раз особое доказательство, что в данном случае тот и другой смысл данного направления безразличны[185]. Если это доказано относительно каждого из направлений пространства, то мы имеем право называть его биполярным, если же безразличие смысла остается под вопросом, или даже отрицается, то такое пространство мы должны считать по тем направлениям, относительно которых безразличие их смысла не доказано, пространством, обладающим свойством униполярности. —Понятие биполярности может быть еще расширено и тогда уже явно отделится от понятия изотропности, если говорить о смысле не направления, т. е. прямой, а о смысле всякого пути между двумя точками. Вообще говоря, прохождение некоторого произвольно выбранного пути между точками А и В от А к 5 — не то же, что от В к А, т. е. в отношении любого пути пространство, если нет особых ограничений, должно считаться униполярным. —Изотропностью характеризуются направления в пространстве, а униполярностью — отрезки этих направлений между двумя точками. Таким образом, для построения понятия об униполярности, необходимы и прямая (шире —вообще линия) и точка, и, следовательно, униполярность имеет связь как с изотропностью, так и с однородностью.

6. Пространство непрерывно и связно. Первоначальное понятие о непрерывности дается указанием на возможность беспредельного деления всякого геометрического образа в пространстве, а о связности — указанием на несуществование в пространстве отдельных, друг от друга уединенных областей, между собою не координированных и не имеющих беспредельного множества путей взаимного сообщения. Однако эти предварительные указания очень недостаточны, и, ограничиваясь ими, мы далеко не выразили бы предносящегося общечеловеческому сознанию понимания непрерывности и связности. — Несравненно более строгая формулировка этого понимания принадлежит Георгу Кантору[186]. Она обнимает оба указанные свойства одним термином Continuum, с тем чтобы расчленить его несколько по–новому. Определение Кантора: «Continuum есть совершенное и связное множество точек». Это тонкое определение, но так как и оно, равно как и последующие усовершенствования его, все‑таки не адекватно интуиции непрерывности и связности, здесь было бы неуместно обсуждать тонкости и контроверзы теории множеств. —В порядке изложения следует отметить лишь, что и непрерывность и связность пространства отнюдь не вытекают аналитически из его понятий и следовательно должны быть доказаны особо. При этом, чем тоньше и глубже проводится логический анализ Continuum'a, тем более частным случаем оказывается пространство евклидовской геометрии. И значит, тем сложнее и потому маловероятнее условия его существования и тем труднее доказательство, что пространство в самом деле таково. Вообще говоря, нет оснований ждать, чтобы пространство имело своими свойствами непрерывность и связность. Из всех возможных случаев непрерывное и связное пространство было бы неожиданной и величайшей редкостью.

7. Пространство трехмерно. Обычное разъяснение трехмерности делается с ссылкою на возможность провести чрез каждую точку пространства три, — не более и не менее как три, —взаимно перпендикулярные прямые. Но такое разъяснение предполагает ряд других свойств, которые в существе дела не связаны необходимо со свойством трехмерности. Поэтому правильнее будет охарактеризовать трехмерность пространства как необходимость и достаточность для точек его определяться тремя, — не более и не менее как тремя, —независимыми друг от друга данными, каковы бы они ни были. Если три данные устанавливают точку в пространстве, два данных или одно недостаточны, так как оставляют возможность бесконечного выбора, а четыре, или большее число данных, если они независимы друг от друга, оказываются, вообще говоря, несовместимыми и друг друга исключающими, то такое пространство обладает свойством трехмерности, если же этого нет, то нет причин называть пространство трехмерным. От других вышеуказанных свойств трехмерность независима и потому должна быть доказываема особо.

8. Пространство однозначно. Три данные или координаты определяют точку в пространстве, т. е. исключают возможность произвольного выбора в том или другом непрерывном геометрическом образе. Однако это не отменяет выбора какого бы то ни было. Определенному сочетанию трех координат может отвечать несколько или даже бесконечное множество различных точек, своею совокупностью не образующих, однако, никакой непрерывности. —Иначе говоря, соответствие точек и координатных триад может быть не однозначным, или во всяком случае, хотя и однозначным, но не взаимно однозначным. Можно мыслить трехмерное пространство таким, что всякой точке или быть может некоторым точкам, соответствует не одна, а множество различных координатных триад; а с другой стороны, можно мыслить пространство, в котором каждой координатной триаде или некоторым соответствует некоторое множество точек. Это будет пространство хотя и трехмерное, но не однозначное. Указанная возможность мыслима и суженною, так, чтобы координатным триадам соответствовали точки однозначно, но не наоборот, или чтобы точкам однозначно соответствовали координатные триады, но триадам соответствие точек было бы многозначное. Итак, вообще говоря, пространство — трехмерное и иное, должно мыслиться вообще говоря многозначным, и лишь на основании особых доказательств может быть признано однозначным. Ясное дело, многозначность пространства есть свойство общее, сравнительно с частным —однозначности, и последнее требует для своего существования особых условий. — Сказанное о точках должно быть повторено с соответственными изменениями также о направлениях в пространстве, в путях и различных геометрических образах, в отношении которых однозначность должна быть всякий раз доказываема особо, тогда как многозначность, вообще говоря, разумеется сама собою. Сюда относится, например, расширение и обогащение понятия о четнои нечетносторонних поверхностях: в связи с существованием, наряду с нормалью, бинормали и тринормали возможны чрезвычайно сложные трехмерные аналогии односторонним и двусторонним поверхностям обыкновенного пространства, но бесконечно более богатые свойствами, подобно тому, как поверхность богаче плоских линий. Наконец, пространство обладает всюду нулевою кривизною. Это свойство пространства не вытекает из предыдущих и должно утверждаться и доказываться особо. Из бесчисленных возможностей различных положительных и отрицательных кривизн, хотя бы и всюду постоянных, нулевая кривизна есть лишь частный случай, и потому доказательство действительности его лежит на том, кто утверждает этот частный случай, тогда как вообще говоря, о кривизне пространства надо говорить как об отличной от нуля. Далее, в главе о полях, понятие кривизны пространства будет рассмотрено более обстоятельно.

IV. ПРОСТРАНСТВО ФИЗИЧЕСКОЕ

1925. V.15

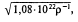
Перечисленными выше признаками характеризуется евклидо–кантовское пространство, т. е. пространство обыкновенной геометрии. Это —то самое пространство, с которым имеет дело рациональная механика. Но пространство физического мира, даже схематически строенное физикою, имеет признаки, существенно отличные от перечисленных выше. Уже основные аксиомы ньютоновской механики, в частности принцип инерции, несовместимы с бесконечностью и некоторыми другими свойствами евклидовского пространства, так что требуется какая‑то перестройка самого понятия пространства. Более глубокая перестройка основ физики на почве обоих принципов относительности повела к существенно отличным от прежних взглядов на пространство, установив его конечность, неоднородность и неизотропность, многомерность (в концепции Эдцингтона — пятимерность), отличие его кривизны от нуля, и притом различное в разных местах, многозначность и, при известном подходе (использование мнимостей), — его несвязность. В дальнейшем можно предвидеть, уже намеченное современной мыслью, отрицание непрерывности на почве теории квантов. Современная физика уже порвала с канто–евклидовским пространством. Достаточно отметить хотя бы эйнштейновский вывод из общей теории относительности о квази–сферичности мирового пространства с радиусом, равным

где ρ есть средняя плотность материи, или подобный же вывод де–Зитмера[187]о конечности времени, или хотя бы результат астрономических исследований Шварцшильда[188] и Гарцера[189] об эллиптичности (в римановском смысле) пространства вселенной с радиусом кривизны, примерно в 100 миллионов раз превосходящим радиус земной орбиты, как представление, согласованное с астрономическим опытом, чтобы убедиться, насколько далека от современной физики евклидовская геометрия. На эту тему можно было бы еще говорить много и показать всесторонне выветривание евклидовского пространства под действием физических исследований. Но в данном случае это не является необходимостью, хотя и могло бы быть полезным дидактическим вступлением для тех, кто в своем мышлении о действительности отправляется от схем и абстракций вместо прямого использования непосредственного опыта. Но поскольку настоящая книга, хотя и общедоступная, предназначена все‑таки тем, кто вниманию своему подвергает действительно переживаемое, а не провозглашаемое таковым в угоду построений схематических, постольку анализ физического пространства здесь был бы скорее вредным, отнимая место у других глав, и подсказывая ложную мысль о необходимости считаться при изучении искусства с выводами физики, и создавая соответственную привычку.

Между тем, в настоящем случае должна быть намечена со всею твердостью полная независимость исследования пространственности в изобразительном искусстве от тех или иных признаний физики; самое большее, они могут дать некоторый аналогон, коренящийся на общих с искусствоведческим исследованием общефилософских и общематематических предпосылках и методах. Наряду с понятием пространства физического установлено таковое же пространства психофизиологического. Оно отвечает, как некоторая схематизация, пониманию пространства нашей повседневной жизни, определяемой психическими и психофизиологическими процессами. Ясное дело, нет никакого основания загодя утверждать тождество пространства психофизиологического с физическим, потому что наша повседневная жизнь не считается с отвлеченными основаниями физики, а физика в своих построениях сознательно отвлекается от явлений психических и психофизиологических.

Таким образом устанавливаются три слоя в понятии пространства: геометрический, физический и психофизиологический, последовательно приближающиеся к пространству конкретному, т. е. к нашему жизненному опыту. Но все они, хотя и в разной мере, отличны от понятия пространства эстетического, той схемы, в которую выкристаллизовывается опыт художника и наблюдателя художественных произведений. Понятие эстетического пространства есть самостоятельный слой в общем понятии о пространстве; самое близкое к понятию эстетического пространства — это понятие пространства психофизиологического, самое далекое от него понятие о пространстве геометрическом, а строемое физикою лежит посредине между обоими.