Второй метод изучения анализа результатов деятельности коммерческих банков – это аналитические группировки, которые исследуют связи и зависимости между изучаемыми явлениями и их признаками.
Аналитическая группировка позволяет выявить наличие или отсутствие зависимости. Вместе с тем в рамках этого метода не удается аналитически описать эту зависимость, а также не удается выяснить "тесноту" или "существенность" этой зависимости.
Метод аналитических группировок применяется для выделения особенностей и дифференцированного регулирования по показателям объема и структуры производства, его концентрации, размещения, эффективности и др.
Используя аналитические группировки, прежде всего, определяют факторные и результативные признаки изучаемых явлений. Факторные - это признаки, оказывающие влияние на другие, связанные с ними признаки. Результативные - признаки, которые изменяются под влиянием факторных. Чтобы исследовать взаимосвязь между отобранными признаками с помощью метода аналитических группировок, необходимо произвести группировку единиц совокупности по факторному признаку и по каждой группе вычислить среднее значение результативного признака, вариация которого от группы к группе под влиянием группировочного признака будет указывать на наличие или отсутствие взаимосвязи.
При сравнении функциональных и корреляционных зависимостей следует иметь в виду, что при наличии функциональной зависимости между признаками можно, зная величину факторного признака, точно определить величину результативного признака. При наличии же корреляционной зависимости устанавливается лишь тенденция изменения результативного признака при изменении величины факторного признака. В отличие от жесткости однозначно функциональной связи корреляционные связи характеризуются множеством причин и следствий и устанавливаются лишь их тенденции.
Статистическое выражение связи между явлениями может показать, что изменения одного из сопоставляемых признаков сопровождаются изменениями другого. Следовательно, нужно искать объяснение этим изменениям в их содержательном анализе. С помощью статистических методов изучения зависимостей можно установить, как проявляется теоретически возможная связь в данных конкретных условиях. *
РАСЧЕТНАЯ ЧАСТЬ
В задание 1 предполагается по данным по 36 банкам построить статистический ряд распределения банков по вложениям в ценные бумаги, образовав 5 групп с равными интервалами.
Таблица 1
Исходные данные
| № банка п/п | Вложения в ценные бумаги | Прибыль | № банка п/п | Вложения в ценные бумаги | Прибыль |
| 1 | 4069 | 110 | 19 | 9087 | 439 |
| 2 | 4279 | 538 | 20 | 8016 | 441 |
| 3 | 3959 | 85 | 21 | 7324 | 237 |
| 4 | 1032 | 60 | 22 | 3445 | 282 |
| 5 | 4152 | 39 | 23 | 2079 | 191 |
| 6 | 5347 | 153 | 24 | 2058 | 201 |
| 7 | 2286 | 215 | 25 | 648 | 12 |
| 8 | 2948 | 224 | 26 | 2673 | 77 |
| 9 | 2914 | 203 | 27 | 3145 | 282 |
| 10 | 1600 | 64 | 28 | 2048 | 451 |
| 11 | 2145 | 11 | 29 | 287 | 50 |
| 12 | 3811 | 153 | 30 | 2571 | 306 |
| 13 | 889 | 121 | 31 | 2081 | 440 |
| 14 | 584 | 94 | 32 | 3787 | 204 |
| 15 | 990 | 105 | 33 | 2131 | 63 |
| 16 | 1618 | 93 | 34 | 7298 | 650 |
| 17 | 1306 | 329 | 35 | 4729 | 538 |
| 18 | 1981 | 451 | 36 | 7096 | 175 |
Построим ряд распределения по среднегодовому вложению в ценные бумаги, образовав 5 групп с равным интервалом.
R= хmax – xmin
i = R / n
i = (9087-287)/5 = 1760 млн. руб.
Формируем группы:
| 1 | 287 | 287+1760 | 2047 |
| 2 | 2047 | 2047+1760 | 3807 |
| 3 | 3807 | 3807+1760 | 5567 |
| 4 | 5567 | 5567+1760 | 7327 |
| 5 | 7327 | и выше |
Делаем разноску предприятий по группам. Если значение показателя соответствует значению верхней границы интервала одной группы и нижнему значению границы интервала другой группы, то эту организацию мы относим к последнему.
Таблица 1
Разработанная таблица
| № п/п | Группы банков по величине вложения в ценные бумаги млн. руб. | Номер банка | Стоимость вложения в ценные бумаги, млн. руб. | Прибыль в млн. руб. |
| 1 | 287-2047 | 4; 10; 13; 14; 15; 16; 17; 18; 25; 29 | 1032; 1600; 889; 584; 990; 1618; 1306; 1981; 648; 287 | 60; 64; 121; 94; 105; 93; 329; 451; 12; 50 |
| 2 | 2047-3807 | 7; 8; 9; 11; 22; 23; 24; 26; 27; 28; 30; 31; 32; 33 | 2286; 2948; 2914; 2145; 3445; 2079; 2058; 2673; 3145; 2048; 2571; 2081; 3787; 2131 | 215; 224; 203; 11; 282; 191; 201; 77; 282; 451; 306; 440; 204; 63 |
| 3 | 3807-5567 | 1; 2; 3; 5; 6; 12; 35 | 4069; 4279; 3959; 4152; 5347; 3811; 4729 | 110; 538; 85; 39; 153; 153; 538 |
| 4 | 5567-7327 | 21; 34; 36 | 7324; 7298; 7096 | 237; 650; 175 |
| 5 | 7327 и выше | 19; 20 | 9087; 8016 | 439; 441 |
| Итого | 36 | 116413 | 8087 |
На основании разработанной таблицы строим ряд распределения.
Таблица 2
Ряд распределения коммерческих банков по стоимости вложения в ценные бумаги
| № п/п | Группы банков по стоимости вложения в ценные бумаги, млн. руб. | Количество банков | Удельный вес банков по группам, в % | Кумулято, количество банков |
| А | 1 | 2 | 3 | |
| 1 | 287-2047 | 10 | 27,8 | 10 |
| 2 | 2047-3807 | 14 | 38,9 | 24 |
| 3 | 3807-5567 | 7 | 19,4 | 31 |
| 4 | 5567-7327 | 3 | 8,3 | 34 |
| 5 | 7327 и выше | 2 | 5,6 | 36 |
| Итого | 36 | 100 | Х |
Анализ таблицы 3.
Наибольшее число банков 24 или 66,7% имеют стоимость вложений в ценные бумаги от 287 до 3807 млн. руб. Наименьшее число банков 2 или 5,6% имеют наибольшую стоимость вложений от 7327 и выше.
Построим графики полученного ряда распределения.
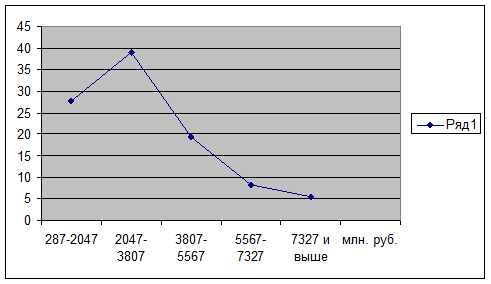
Рис. 1. Кумулята распределения банков по вложению средств в ценные бумаги
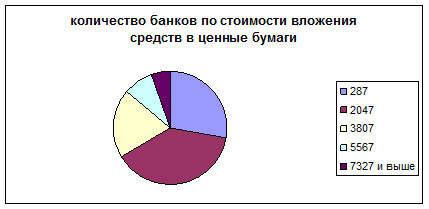
Рис. 2 Количество банков по стоимости вложения в ценные бумаги
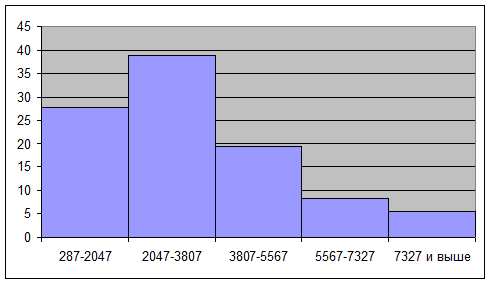
Рис.3 Гистограмма распределения банков по вложению средств в ценные бумаги
Рассчитаем характеристики интервального ряда распределения:
а) Средняя арифметическая
- простая
Xар = ∑x / n = 116413/36 = 3233,69 млн. руб.
Χар(взв) = ∑xf / ∑f
(287+2047)/2 = 1167;
(2047+3807)/2 = 2927;
(3807+5567)/2 = 4687;
(5567+7327)/2 = 6447;
(7327+9087)/2 = 8207
Χар(взв) = (1167*10+2927*14+4687*7+6447*3+8207*2)/36 = 121212/36 = 3367 млн. руб.
Рассчитаем среднеквадратное отклонение:
σ² = Σ(xx)²f/Σf
(1167-3233,69)² *10 = 42712075,60
(2927-3233,69)²* 14 = 1316822,64
(4687-3233,69)²* 7 = 14784769,72
(6447-3233,69)²* 3 = 30976083,48
(8207-3233,69)²* 2 = 49467624,72
139257376,16
= 139257376,16/36 = 3868260,45
δ = ± 1966,79 млн. руб.
Рассчитываем коэффициент корреляции:
V = δ*100/х = 1966,79*100/3233,69 = 60,82 %
Коэффициент корреляции равен 60,82 % говорит о том, что ряд распределения банков по стоимости вложения средств в ценные бумаги не однороден, так как превышает 33 %, а средняя стоимость вложений средств в ценные бумаги равна 3233,69 млн. руб. типична и надежна для данного ряда распределения. Колеблемость в ряду распределения значительна, так как превышает 60 %.
Рассчитаем моду и медиану для интервального ряда.
Мо = 2047+1760*(14-10) / (14-10)+(14-7) = 2047+1760+7 = 3814,00 млн. руб.
Наибольшее число банков имеет среднегодовое вложение средств в ценные бумаги 3814,00 млн. руб.
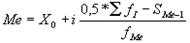
Ме = 2047+1760*(36/2-10)/14 = 3052,71 млн. руб.
Вывод: медиана равна 3052,71 млн. руб. говорит о том, что половина банков имеет стоимость вложения средств в ценные бумаги до 3052,71 млн. руб., а остальные – более 3814,00 млн. руб.
Задание № 2
1) Строим аналитическую группировку на основании разработочной таблицы
Таблица 3
Группировка банков по стоимости вложений средств в ценные бумаги
| № п/п | Группы банков по стоимости вложений в ценные бумаги, млн. руб. | Количество банков | Стоимость вложений в ценные бумаги, млн. руб. | Прибыль банков, млн. руб. | ||
| всего | В 1 банке | всего | В 1 банке | |||
| А | 1 | 2 | 3 | 4 | 5 | |
| 1 | 287-2047 | 10 | 10935 | 1093,50 | 1379 | 137,90 |
| 2 | 2047-3807 | 14 | 36311 | 2593,64 | 3150 | 225,00 |
| 3 | 3807-5567 | 7 | 30346 | 4335,14 | 1616 | 230,86 |
| 4 | 5567-7327 | 3 | 21718 | 7239,33 | 1062 | 354,00 |
| 5 | 7327 и выше | 2 | 17103 | 8551,50 | 880 | 440,00 |
| Итого | 36 | 116413 | 3233,69 | 8087 | 224,64 | |
Из данных таблицы 2 следует, что с увеличением вложений средств в ценные бумаги от 1 к 5 группе в среднем на 1 банк увеличивается и прибыль. Это свидетельствует о наличии прямой связи между вложением средств в ценные бумаги и прибылью банков.
Вложения в ценные бумаги 5 группы по отношению к 1 группе в расчете на 1 банк составляет 7,89 раза, а прибыль на 1 банк в 5 группе больше чем в 1 в 3,19 раза. Разные темпы роста этих показателей свидетельствуют о наличии корреляционной зависимости между вложениями и прибылью – прямая корреляционная связь.
На основании данных аналитической группировки делается расчет показателей тесноты связей.
Расчет коэффициента детерминации:
η2 = δ2 /σ2 = 6068,69/27450,56 = 0,22
Рассчитаем дисперсию, делаем по результативному признаку – прибыль
δ2 = ∑(у –у)2f /∑f = ((137,90-224,64)²*10+(225-224,64)²*14+(230,86-224,64)²*7+(354-224,64)²*3+(440-224,64)²*2)/36 = 6068,69
Делаем разработочную таблицу, где у – это сумма прибыли в каждом банке
Таблица 2
Разработочная таблица
| № п/п |
Прибыль млн. руб., у
у2
1
110
12100
2
538
289444
3
85
7225
4
60
3600
5
39
1521
6
153
23409
7
215
46225
8
224
50176
9
203
41209
10
64
4096
11
11
121
12
153
23409
13
121
14641
14
94
8836
15
105
11025
16
93
8649
17
329
108241
18
451
203401
19
439
192721
20
441
194481
21
237
56169
22
282
79524
23
191
17381
24
201
40401
25
12
144
26
77
5929
27
282
79524
28
451
203401
29
50
2500
30
306
93636
31
440
193600
32
204
41616
33
63
3969
34
650
422500
35
538
289444
36
175
30625
2804893
σ2 = у2 – у2, где у2 = ∑у2 /n
у2 = ∑у2 /n = 2804893/36 = 77913,69
σ2 = у2 – у2 = 77913,69-50463,13 = 27450,56
Вывод по коэффициенту детерминации:
Коэффициент детерминации свидетельствует о том, что прибыль на 22 % определяется вложением в ценные бумаги.
Империческое корреляционное отношение:
Ŋ = √ η2 = √0,22 = 0,47
Вывод: этот коэффициент свидетельствует о том, что связь между вложением в ценные бумаги и прибылью весьма тесна.
Задание 3
1) Находим предельную ошибку выборки:
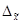= t 
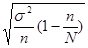=2*322,84 = ± 645,69 млн. руб.
Средний уровень вложений средств в ценные бумаги будет находиться в границах, которые мы находим по формуле:
≤ 
≤ 
+ .
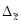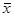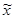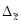3233,69-645,69<= 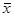>= 3233,69+645,69
2588,00 млн. руб. <=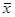 
>= 3879,38 млн. руб.
Вывод.
С вероятностью 0,954 можно утверждать, что средняя величина вложений в ценные бумаги всех банков будет находиться в пределах от 3811 млн. руб. и более.
 |
2) Определим долю банков.
 |
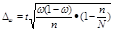Выборочная доля составит:
Ω = 26/36 = 0,72
Ошибку выборки определяем по формуле:
 |
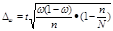где N – объем генеральной совокупности.
∆ω = 2*0,074 = 0,147
72-14,7<=p>=72+14,7
57,3<=p>=86,7
Вывод: с вероятностью 0,954 можно утверждать, что доля банков, имеющих среднегодовое вложение средств в ценные бумаги 2047 млн. руб. и более, генеральная совокупность будет находиться в пределах от 57,3% до 86,7%.
Задание 4
Имеются следующие данные по коммерческому банку о просроченной задолженности по кредитным ссудам:
Год
Дата: 2019-07-24, просмотров: 237.
