Основной задачей прогнозирования дивидендных выплат является проверка того, что компания будет способна в обозримом будущем выплатить все причитающиеся по привилегированным акциям дивиденды точно в срок и в полном объеме. Для подтверждения этого инвестор должен быть уверен в способности компании получать прибыль, т.к. дивиденды по привилегированным акциям выплачиваются из прибыли компании или из резервного фонда, создаваемого предприятием.
Для оценки привилегированных акций российских компаний особенно важен процесс определения прогнозной величины прибыли компании, т.к. дивиденды по данным акциям выплачивается в процентах (как правило, 10% для привилегированных акций типа А и 5% для привилегированных акций типа Б) от величины чистой прибыли акционерного общества, полученной за последний год.[[19]]
В результате прогнозирования величины чистой прибыли компании в прогнозном периоде, получаем расчетную величину дивидендного потока за каждый год прогнозного периода (10% или 5% от величины чистой прибыли), который необходимо продисконтировать по некоторой ставке дисконтирования.
Определение ставки дисконтирования
Под ставкой дисконтирования при определении стоимости финансового актива понимается средняя ставка доходности всех альтернативных инвестиций со сравнимым уровнем риска.
Часто (как правило, при определении средневзвешенной ставки по модели WACC для оценки бизнеса методом дисконтирования денежных потоков для всего инвестированного капитала) в литературе можно встретить рекомендации: в качестве затрат на привлечение капитала за счет выпуска привилегированных акций использовать норму их дивидендной доходности.[[20]]
Однако такой подход, особенно в российских условиях, не представляется вполне корректным: данный подход возможен только в случае оценки давно и устойчиво функционирующего предприятия, занявшего определенную позицию на традиционном и развитом рынке в условиях стабильной экономики.
В качестве примера можно привести оценки уровня дивидендных выплат по привилегированным акциям крупнейших российских компаний (Таблица 4.), которые достаточно активно обращаются на организованном фондовом рынке - РТС (здесь и далее уровень ставок приводится для долларовых инвестиций). Уровень дивидендных выплат определялся как процентное отношение суммы выплаченного дивиденда к рыночной стоимости акции.
Таблица 4.
| Эмитент | 1996г. | 1997г. | 1998г. | 1999г. | 2000г. |
| "Сургутнефтегаз" | 9,56% | 1% | 1,87% | 2,04% | 5,17% |
| "Ростелеком" | 4,91% | 3,85% | 0% | 2,33% | 4,6% |
| "РАО "ЕЭС России" | 0,18% | 0,76% | 1,61% | 1,45% | 6,36% |
| "ЛУКОЙЛ" | 2,38% | 1,17% | 4,29% | 6,25% | 18,04% |
| "Норильский никель" | 0,01% | 0,03% | 0% | 0,1% | 0,59% |
Как видно из таблицы, норма дивидендных выплат российских эмитентов крайне невелика (за исключением ОАО "ЛУКОЙЛ" в 2000 году) и значительно меньше уровня ставок привлечения заемных средств (например, доходность российских еврооблигаций, выпущенных Минфином РФ, даже в период наивысшего инвестиционного рейтинга страны не опускалась ниже 10-11%.
В качестве одной из самых адекватных и широко применимых моделей расчета ставки дисконтирования возможно использование модели оценки капитальных активов (САРМ).
Модель CAPM
Как правило, модель САРМ применяют для оценки стоимости привлечения акционерного капитала, подразумевая владельцев обыкновенных акций компании. Однако данная модель носит общий характер, позволяя рассчитать ставку требуемой доходности для любого финансового актива, в том числе и привилегированных акций. Общая формула модели САРМ:[[21]]
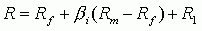
где Rf - безрисковая ставка доходности,
βi - коэффициент бэта,
Rm - среднерыночная доходность,
Rl- премия за инвестирование в конкретную компанию.
Под безрисковой ставкой подразумевается ставка, по которой привлекают средства наиболее надежные заемщики в условиях конкретной страны. Безрисковая ставка не является абсолютно безрисковой, но предполагает минимальный риск кредитора в определенном государстве.
Поскольку обыкновенные и привилегированные акции одной и той же компании представляют собой различные инструменты и удостоверяют различный объем прав, то вполне естественно, что мотивы инвесторов, приобретающих эти бумаги, различны, что ведет соответственно к различию динамики поведения рыночных цен на разные виды акций. Поэтому значения коэффициентов β для обыкновенных и привилегированных акций должны различаться, более того, для привилегированных акций β должна быть меньше (поскольку меньше риски инвесторов).
Для иллюстрации данного утверждения автором были рассчитаны значения β для обыкновенных и привилегированных акций ряда российских эмитентов, имеющих достаточно долгую историю котировок, по которым регулярно совершались реальные сделки, т.е. акции имели достаточно высокий уровень ликвидности (Таблица 5.).
Таблица 5.
| Эмитент | Обыкновенные акции | Привилигированные акции |
| "Сургутнефтегаз" | 1,1 | 1,06 |
| РАО "ЕЭС России" | 1,35 | 1,31 |
| "Ростелеком" | 1,32 | 1,1 |
| "ЛУКОЙЛ" | 0,99 | 1,09 |
| "Норильский Никель" | 1,07 | 1,01 |
| "Татнефть" | 1,23 | 0,45 |
| "Сбербанк РФ" | 1,16 | 0,92 |
В приведенной выше таблице значения β определялись без учета корректировки на соотношение заемных и собственных средств, а в качестве рыночной доходности была использована доходность фондового индекса РТС. Полученные данные показывают, что выдвинутое предположение вполне подтверждается.
Премию за риск следует определять как разность между среднерыночной доходностью и безрисковой ставкой. Для расчета среднерыночной доходности в долларовом эквиваленте необходимо использовать значения фондового индекса РТС (как основного индикатора уровня цен рынка российских акций в долларовом эквиваленте) за пять полных лет с момента начала торгов в РТС. Средняя доходность рынка за указанный период (рассчитанная как средняя геометрическая) равна 18,85% годовых (источник: рассчитано автором). Соответственно, премия за риск равняется 6,85-8,85%.
Последним компонентом формулы является премия за риск инвестирования в конкретную компанию. Премия учитывает следующие факторы:[[22]]
· риск инвестирования в малую компанию,
· риск нарушения прав акционеров,
· риск финансового состояния,
· прочие хозяйственные риски (диверсификация производства и сбыта, стабильность и предсказуемость доходов, качество управления).
Далее, на основании прогноза величины дивидендов и рассчитанной ставки дисконтирования можно рассчитать первую часть рыночной стоимости привилегированных акций в рамках доходного подхода.
Вторая часть стоимости - стоимость опциона будет рассчитана с помощью 3-х моделей, краткое описание которых приводится ниже.
Модель Шелтона
Шелтон доказывает, что существует минимальная и максимальная стоимость опциона. Минимальная цена должна соответствовать внутренней стоимости опциона, которая не может быть меньше нуля, потому что опцион не обязывает владельца к исполнению. Если цена опциона падает ниже его внутренней стоимости, инвесторы будут покупать опцион и исполнять его, до тех пор пока цена опциона не вернется к его внутренней стоимости, и будут покупать акции по цене ниже их текущей рыночной цены.
Модель Шелтона предполагает, что если цена акции в 4 раза больше цены исполнения опциона, опцион будет продаваться выше его внутренней стоимости. Кроме того, Шелтон предполагает, что максимальная цена опциона составляет 3/4 цены акции.
Используя метод регрессионного анализа Шелтон определил, что плотное сближение цен долгосрочных опционов, получается с помощью регулирующего фактора, рассчитываемого следующим образом:[[23]]
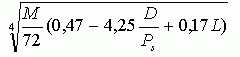
|
где M - количество месяцев, оставшихся до исполнения опциона,
D - годовые дивиденды по акции,
Ps - текущая цена акции,
L = 1 если опцион котируется на бирже и 0, если он торгуется на внебиржевом рынке.
Минимальная стоимость опциона - это его внутренняя стоимость, которая определяется путем вычитания текущей цены акции из цены исполнения. Максимальная стоимость равна 3/4 от текущей цены акции.
Стоимость опциона по модели Шелтона определяется по следующей формуле: Минимальная стоимость + (регулирующий фактор)*(максимальная стоимость - минимальная стоимость) = стоимость опциона
Один недостаток формулы Шелтона заключается в том, что она не делает поправки на исторические колебания цены акции. Шелтон проверил фактор волатильности в своем первоначальном исследовании, но не выявил того, что и он влияет на стоимость опциона, тогда как другие факторы были включены в алгоритм расчета.
Модель Блэка-Шоулза
Формула Блэка-Шоулза использует следующую формулу:[[24]]
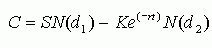
|
где C - теоретическая стоимость опциона,
S - текущая цена базовых акций,
t - время, остающееся до срока истечения опциона, выраженное как доля года (количество дней до даты истечения/365 дней),
K - цена исполнения опциона,
r - процентная ставка по безрисковым активам,
N(x) - кумулятивное стандартное нормальное распределение,
e - экспонента (2,7183).
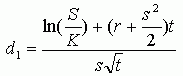
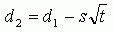
S - годовое стандартное отклонение цены базовых акций (историческая волатильность),
ln - натуральный логарифм.
Для понимания сути модели ее целесообразно разделить на две части. Первая часть, SN(d1) отражает ожидаемую прибыль от покупки самих базовых акций. Расчет производится через умножение цены лежащих в основе акций S на изменение премии по опциону колл по отношению к изменению цены базового актива N(d1).
Вторая часть модели Ke(-rt)N(d2) дает приведенную стоимость цены исполнения на дату истечения опциона. Объективная рыночная стоимость опциона колл рассчитывается путем вычитания второй части формулы из первой.[[25]]
Модель Норина - Вольфсона
Предположения, используемые в модели Норина-Вольфсона - вариации модели Блэка-Шоулза - примерно такие же, как и в самой модели Блэка-Шоулза. Однако два различия должны быть отмечены. Первое, модель Норина-Вольфсона учитывает выплаты дивидендов и предполагает, что они выплачиваются постоянно. Второе, модель рассматривает возможное уменьшение стоимости опциона до момента его исполнения.
Модель имеет ту же форму и использует те же определения переменных, которые использовались в модели Блэка-Шоулза, за исключением некоторых различий:[26]
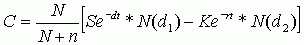
N - количество выпущенных обыкновенных акций,
n - количество обыкновенных акций, которые будут выпущено, если варранты будут исполнены,
d - постоянный дивидендный доход,
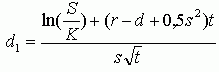
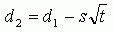
|
Эта вариация модели Блэка-Шоулза имеет несколько таких же проблем, что и у оригинальной модели. Однако, модель Норина-Вольфсона отражает дивиденды и учитывает возможное уменьшение стоимости опциона, которое может случиться до его исполнения.
Дата: 2019-07-24, просмотров: 338.