Коэффициент теплопередачи для первого корпуса определяем по уравнению аддитивности термических сопротивлений:
К1=(1/α1+Σδ/λ+1/α2)-1. (3.8)
Примем, что суммарное термическое сопротивление равно термическому сопротивлению стенки δст/λст и накипи δн/λн
Термическое сопротивление загрязнений со стороны пара не учитываем. Получим:
Σδ/λ=δст/λст+δн/λн (3.9)
где δст, δн - толщина стенки, толщина слоя накипи, м.
при δст=0,002 м.
при δн=0,0005 м.
где λст, λн - коэффициент теплопроводности стенки и накипи, Вт/(м∙К).
при λст=25,1 Вт/(м*К).
при λн=2 Вт/(м*К).
Σδ/λ=0,002 /25,1+0,0005/2=2,87 ∙10-4 м2*К/Вт.
Коэффициент теплоотдачи от конденсирующего пара к стенке α1 равен:
α1=2,04∙((r1∙ρж12∙λж13)/(μж1∙Н∙Δt1))1/4. (3.10)
где r1 - теплота конденсации греющего пара, Дж/кг;
рж1, λж1, μж1 - соответственно плотность (кг/м3), теплопроводность Вт/(м*К), вязкость (Па*с) конденсата при средней температуре пленки:
tпл=tг1-Δt1/2
где Δt1 - разность температур конденсации пара и стенки, °С.
Расчет α1 - ведем методом последовательных приближений.
В первом приближении примем Δt1=2 °С. Тогда
tпл=142.9-2/2=141,9°С.
α1=2,04∙(2144∙103 ∙10322∙0,4083/0,19∙10-3∙4∙2)1/4=6484 Вт/(м2∙К)
Для установившегося процесса передачи тепла справедливо уравнение:
q=α1∙Δt1=Δtст/(ΣΔδ/λ)=α2∙Δt2, (3.11)
где q - удельная тепловая нагрузка, Вт/кв.м;Δtcт - перепад температур на стенке, °С;Δt2 - разность между температурой стенки со стороны раствора и температурой кипения раствора, °С.
Отсюда:
Δtст=α1∙Δt1∙(Σδ/λ)=6484∙2∙2,87∙10-4 =3,72°С.
Тогда
Δt2=Δtп1-Δtст-Δt1=20,08-3,72-2=16,36°С.
Коэффициент теплопередачи от стенки к кипящему раствору для пузырькового кипения в вертикальных кипятильных трубках при условии естественной циркуляции раствора равен:
α2=А∙(q0,6)=780∙(q0,6)∙(λ11,3)∙(ρ10,5)∙(ρп10,06)/((с10,3)∙(σ10,5)∙(гв10,6)∙(ρ00,66)∙(μ10,3))(3.12)
По справочной литературе определяем:
λ1=0,4159 Вт/(м∙К); ρ1=1068 кг/м3; ρп1=1,22 кг/м3; σ1=0,067 Н/м; гв1=2200∙103 Дж/кг; ρ0=0,529 кг/м3; с1=4095 Дж/кг∙К; μ1=0,265∙10-3 Па∙с
Подставив эти значения, получим:
α2=780∙(q0,6)∙0,41591,3∙10680,5∙1,220,06/0,0670,5∙(2200∙103)0,6∙0,5290,66∙
40950,3∙(0,265∙10-3)0,3=7,408∙(6484)0,6=1435 Вт/(м2∙К)
Проверим правильность первого приближения по равенству удельных тепловых нагрузок:
q1=α1∙Δt1=6484∙2=12968 Вт/кв.м
q2=α2∙Δt2=1435∙16,36=2348 Вт/кв.м
q1≠q2
Для второго приближения примем Δt1=5,0 град
Пренебрегая изменением физических свойств конденсата при изменении температуры на 3,0 град, рассчитаем α1 по соотношению:
α1=6484∙(2/5)1/4=5156 Вт/(м2∙К)
Получим:
Δtст=5156∙5∙2,87∙10-4=7,4 град;
Δt2=20,08-5-7,4=7,68 град;
α2=7,408*(5156∙5)0,6=3285 Вт/(м2∙К)
q1=5156∙5=25780 Вт/м2
q2=3285∙7,68=25229 Вт/м2
q1≈q2
Расхождение между тепловыми нагрузками не превышает 3%, следовательно, расчет коэффициентов α1 и α2 на этом можно закончить.
Находим К1:
К1=(1/5156+2,87∙10-4+1/3285)-1=1271 Вт/(м2∙К).
Далее рассчитываем коэффициент передачи для второго корпуса К2.
В первом приближении примем Δt1=4 °С. Тогда:
Δtпл=120. 3-2/2=118.3°С
α1=2,04∙(2210∙103 ∙1133∙0.4265/4∙4∙0.335∙10-3)1/4=5164 Вт/м2К
Δtст=5164∙4∙2,87∙10-4=5,93°С
Δt2=57,01-4-5,93=47,08°С
α2=780∙(q0,6)∙0,43661/3∙11870,5∙0,150,06/0,0960,5∙(2350*103)0,6 0,5290,66 ∙35090,3∙(0,851∙10-3)0,3 = 4,34(388∙4)0,6=1683 Вт/м2∙К
Проверим правильность первого приближения по равенству удельных тепловых нагрузок:
q1=α1∙Δt1=5164∙4=20656 Вт/м2
q2=α2∙Δt2=1683∙47,08=79236 Вт/м2
q1≠q2
Используя вышеописанный метод приближения, найдем:
Δt1=18.65°С
α1=5164∙(4/18,65)1/4=3514 Вт/м2К
Δtст=3514∙18,65∙2,87∙10-4=18,81°С
Δt2=57,01-18,81-18,65=19,55°С
α2=4,34∙(3514∙18,65)0,6=3368 Вт/м2∙К
q1=65536 Вт/м2
q2=65845 Вт/м2
q1≈q2
Определим К2:
К2=(1/3514+2,87*10-4+1/3368)-1=1151 Вт/м2∙К
Распределение полезной разности температур
Полезные разности температур в корпусах установки находим из условия равенства их поверхностей теплопередачи:
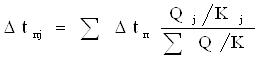 , (3.13)
, (3.13)
где Δtп j, Qj, Kj - соответственно полезная разность температур, тепловая нагрузка, коэффициент теплопередачи для j-го корпуса.
Подставив численные значения, получим:
Δtп 1=77,09∙(6292/1271)/(6292/1271+4080/1151)=44,92 град;
Δtп 2=77,09∙(4080/1151)/(6292/1271+4080/1151) =32.17 град.
Проверим общую полезную разность температур установки:
Σ Δtп=Δtп1 +Δtп2 =44,92+32,17=77,09 °С
Рассчитаем поверхность теплопередачи выпарного аппарата по формуле (3.1):
F1=6292∙103/1271∙44,92=110,2 м2;
F2=4080∙103 /1151∙32.17=110,2 м2.
В последующих приближениях нет необходимости вносить коррективы на изменение конструктивных размеров аппаратов. Сравнение распределенных из условий равенства поверхностей теплопередачи и предварительно рассчитанных значений полезных разностей температур Δtп представлено в табл. 2:
Таблица 2
| Параметры | Корпус | ||
| 1 | 2 | ||
| Распределенные в 1-ом приближении Δtп, град. | 44,92 | 32.17 | |
| Предварительно рассчитанные Δtп,град | 20,08 | 57,01 | |
Второе приближение
Как видно, полезные разности температур, рассчитанные из условия равного перепада давления в корпусах и найденные в 1-ом приближении из условия равенства поверхностей теплопередачи в корпусах, существенно различаются. Поэтому необходимо заново перераспределить температуры(давления) между корпусами установки. В основе этого перераспределения температур(давлений) должны быть положены полезные разности температур, найденные из условия равенства поверхностей теплопередачи аппаратов.
Дата: 2019-07-24, просмотров: 331.