1. Распределительный закон умножения по отношению к сложению (умножение суммы чисел на число).

.

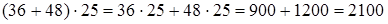Чтобы умножить сумму нескольких чисел на данное число, достаточно умножить каждое слагаемое на это число и полученные произведения сложить.

К указанному способу по обоснованию приема близок способ вынесения за скобки общего множителя или множимого.

1) ;

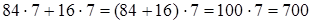2) .

2. Распределительный закон умножения по отношению к вычитанию (умножение разности чисел на число).

1) .

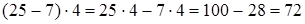Чтобы умножить разность чисел на какое-нибудь число, достаточно умножить на это число отдельно уменьшаемое и вычитаемое и из первого произведения вычесть второе.

2) .

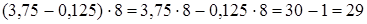К указанному способу по обоснованию приема близок способ вынесения за скобки общего множителя.

3. Умножение суммы на сумму.

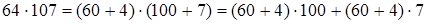 (умножение числа на сумму) = .

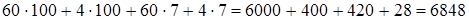Чтобы умножить сумму нескольких чисел на другую сумму, можно каждое слагаемое первой суммы умножить на каждое слагаемое второй суммы и полученные произведения сложить.

Умножение и деление

1. Перестановка членов ряда умножений и делений (переместительность ряда умножений и делений).

1) 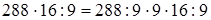 (если данное число разделить на какое-нибудь число и затем полученное частное умножить на это же число, то данное число останется без изменения) = 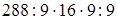(переместительность умножения) =  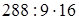(если данное число умножить на какое-нибудь число, отличное от 0, и затем полученное произведение разделить на это же число, то данное число останется без изменения) =512 (правило порядка действий: действия одной и той же ступени (при отсутствии скобок) выполняются в том порядке, в каком они записаны).

2) 486: 9: 2 = 486: 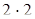: 9: 2 (если данное число разделить на какое-нибудь число и затем полученное частное умножить на это же число, то данное число останется без изменения) = 486: 2: 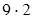: 2 (переместительность членов ряда умножений и делений) = 486: 2: 9 (если данное число умножить на какое-нибудь число (не равное нулю) и затем полученное произведение разделить на это число, то данное число останется без изменения) = 243: 9 = 27.

Результат ряда умножений и делений не меняется от перемены порядка членов данного ряда (разумеется, что каждый член ряда остается в своей прежней роли, иначе говоря, переносится на другое место вместе с написанным перед ним знаком действия).

2. Умножение числа на частное.

1) 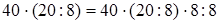 (если данное число умножить на какое-нибудь число (не равное нулю) и затем полученное произведение разделить на это же число, то данное число остаются без изменения) = 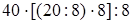(сочетательность умножения) =  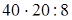(если данное число разделить, на какое-нибудь число и затем полученное частное умножить на это же число, то данное число останется без изменения) = 800: 8 = 100 (порядок действий). Итак, .

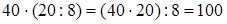Чтобы умножить число на частное, можно умножить его на делимое, и полученное произведение разделить на делитель.

2) .

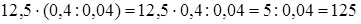3. Деление числа на произведение.

1) 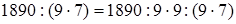(если данное число разделить на какое-нибудь число и полученное частное умножить на то же самое число, то данное число останется без изменения) =  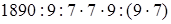(объяснение то же) =  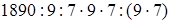(переместительность умножения) =  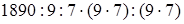(сочетательность умножения) = 1890: 9: 7 (если данное число умножить на какое-нибудь число (не равное нулю) и затем полученное произведение разделить на это же число, то данное число останется без изменения) = 210: 7 = 30 (порядок действий).

Чтобы разделить число на произведение нескольких чисел, достаточно разделить его на первый сомножитель, полученное частное – на второй, новое частное – на третий и т.д. до конца.

2) 8,16: ( 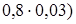 = 8,16: 0,8: 0,03 = 10,2: 0,03=340.

К указанным способам близки по обоснованию приема следующие: разложение делителя на множители и замена нескольких делителей их произведением.

3) 1890: 54 = 1890: ( 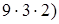= (1890: 9): 3: 2 = (210: 3): 2 = 70: 2 = 35.

4) 2800: 25: 8 = 2800: ( 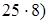= 2800: 200 = 14.

4. Деление произведения на число.

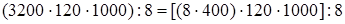 (так как 3200 = 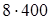) = 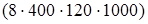: 8 (порядок действий) =  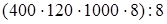(переместительность умножения) =  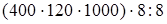(сочетательность умножения) =  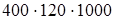(если данное число умножить на какое-нибудь число (не равное нулю) и затем полученное произведение разделить на это же число, то данное число останется без изменения) =  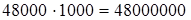(порядок действий).

Чтобы разделить произведение нескольких чисел на какое-нибудь число, достаточно разделить на это число один из сомножителей, оставив другие без изменения.

5. Деление произведения нескольких чисел на другое произведение.

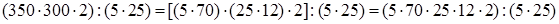
(следствие сочетательного закона) = 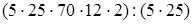 (переместительность умножения  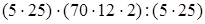(сочетательность умножения) = 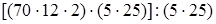(переместительность) =  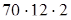(деление произведения на число) = 1680 (умножаем полученные числа).

Чтобы разделить произведение нескольких чисел на другое произведение, все сомножители которого входят в состав первого произведения, достаточно разделить, каждый из сомножителей первого произведения на соответствующий сомножитель второго произведения, а затем полученные частные и оставшиеся сомножители перемножить.

6. Деление числа на частное.

3200: (800: 32) = 3200: 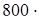 800: (800: 32) (если данное число разделить на какое-нибудь число, а затем полученное частное умножить на это же число, то данное число останется без изменения)
= 3200: 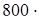 32: 32 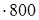: (800: 32) (если данное число умножить на какое-либо число (не равное нулю), а затем полученное произведение разделить на это же число, то данное число останется без изменения)
= 3200: 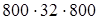: 32: (800: 32) (переместительность ряда умножений и делений) = 3200: 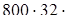(800: 32): (800: 32) (сочетательность ряда умножения и деления) = 3200:  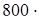32 (если данное число умножить на какое-нибудь число (не равное нулю), а затем полученное произведение разделить на это же число, то данное число останется без изменения) = 4  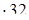= 128 (делим и умножаем полученные числа).

Чтобы разделить число на частное, достаточно разделить его на делимое, а затем полученное частное умножить на делитель.