Навыки устных вычислений формируются в процессе выполнения учащимися разнообразных упражнений. Рассмотрим основные их виды [1].
1) Нахождение значений математических выражений.
Предлагается в той или иной форме математическое выражение, требуется найти его значение. Эти упражнения имеют много вариантов. Можно предлагать числовые математические выражения и буквенные (выражение с переменной), при этом буквам придают числовые значения и находят числовое значение полученного выражения, например:
· найдите разность чисел 100 и 9;
· найдите значение выражения 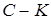 , если С = 100, К = 9.
, если С = 100, К = 9.
Выражения могут предлагаться в разной словесной форме:
· из 100 вычесть 9; 100 минус 9;
· уменьшаемое 100, вычитаемое 9, найдите разность;
· найти разность чисел 100 и 9;
· уменьшить 100 на 9 и т.д.
Эти формулировки использует не только учитель, но и ученики.
Выражения могут включать одно и более действий. Выражения с несколькими действиями могут включать действия одной ступени или разных ступеней, например:
· 47 + 24 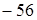 ;
;
· 72: 12 · 9.
Могут быть действия со скобками или без скобок: ( 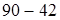 ): 3,
): 3, 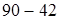 : 3. Как и выражения в одно действие, выражения в несколько действий имеют разную словесную формулировку, например:
: 3. Как и выражения в одно действие, выражения в несколько действий имеют разную словесную формулировку, например:
· из 90 вычесть частное чисел 42 и 3;
· уменьшаемое 90, а вычитаемое выражено частным чисел 42 и 3.
Выражения могут быть заданы в разной области чисел: с однозначными числами, с двузначными, с трехзначными и т.д., с натуральными числами и величинами. Однако, как правило, приёмы устных вычислений должны сводиться к действиям над числами в пределах 100. Так, случай вычитания четырехзначных чисел сводится к вычитанию двузначных чисел и, значит, его можно предлагать для устных вычислений.
Выражения можно давать и в форме следующей таблицы
| Уменьшаемое | 12 | 14 | 35 | 12 | 28 |
| Вычитаемое | 10 | 8 | 15 | 5 | 10 |
| Разность |
Основное значение упражнений на нахождение значений выражений – выработать у учащихся твердые вычислительные навыки, а также они способствуют усвоению вопросов теории арифметических действий.
2) Сравнение математических выражений.
Эти упражнения имеют ряд вариантов. Могут быть даны два выражения, а надо установить, равны ли их значения, а если не равны, то какое из них больше или меньше: 6 + 4 * 4 + 6, 20 + 7 * 20 + 5, 20 · 8 * 18 · 10, 8 · 9 * 8 · 10. Вместо * необходимо поставить знак <, > или =.
Могут предлагаться упражнения, в которых уже дан знак отношения и одно из выражений, а другое выражение надо составить или дополнить:
8 · (10 + 2) = 8 · 10 +…
Выражения таких упражнений могут включать различный числовой материал: однозначные, двузначные, трехзначные числа и величины. Выражения могут быть с разными действиями.
Главная роль таких упражнений – способствовать усвоению теоретических знаний об арифметических действиях, их свойствах, о равенствах, о неравенствах и др. Также они помогают выработке вычислительных навыков.
3) Решение уравнений.
Это прежде всего простейшие уравнения (х + 2 = 10) и более сложные.
Уравнение можно предлагать в разных формах:
· решение уравнения 24: х = 3;
· из какого числа надо вычесть 18, чтобы получить 40?
· найдите неизвестное число: 73 + х = 73 + 18
· я задумала число, умножила его на 5 и получила 85. Какое число я задумала?
Назначение таких упражнений – выработать умение решать уравнение, помочь учащимся усвоить связи между компонентами и результатами арифметических действий.
4) Решение задач.
Для устной работы предлагаются и простые и составные задачи.
Эти упражнения включаются с целью выработки умений решать задачи, они помогают усвоению теоретических знаний и выработке вычислительных навыков.
Разнообразие упражнений возбуждает интерес у детей, активизирует их мыслительную деятельность.
Дата: 2019-07-24, просмотров: 300.