Понятие математических навыков

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Содержание

Введение

1. Требования к вычислительным умениям и навыкам учащихся

1.1 Понятие математических навыков

1.2 Требования к вычислительным умениям и навыкам

1.3 Устные вычисления как основа повышения вычислительной культуры школьников

2. Методика повышения вычислительной культуры школьников

2.1 Организация устных вычислений учащихся

2.2 Приемы устных вычислений, основанные на законах и свойствах арифметических действий

2.3 Приемы устных вычислений, основанные на изменении результата действий в зависимости от изменения компонентов

2.4 Систематизация приемов повышения вычислительной культуры для практической работы учителя

2.5 Содержание и анализ опытно-экспериментальной работы

Заключение

Библиографический список

Введение

Развитие общества требует постоянного улучшения качества обучения, трудового и нравственного воспитания учащихся. Поэтому, важнейшей задачей обучения математике является обеспечение прочного и сознательного овладения учащимися математическими знаниями и умениями, нужными в повседневной жизни и в работе каждого члена современного общества.

В связи с этим необходимо подчеркнуть роль вычислительной подготовки учащихся в системе общего образования. Вычислительная культура является тем запасом знаний и умений, который находит повсеместное применение, является фундаментом изучения математики и других учебных дисциплин. Кроме того, вычисления активизируют память учащихся, их внимание, стремление к рациональной организации деятельности и прочие качества, оказывающие существенное влияние на развитие учащихся.

Однако, во время проведения в ходе педагогической практики пробных уроков, и наблюдений за уроками математики, которые проводили мои однокурсники, и которые проводила я сама, из беседы с учителями математики можно сделать вывод о том, что уровень навыков вычислений и тождественных преобразований у учащихся резко снизился: они плохо и нерационально считают, кроме того, при вычислениях все чаще прибегают к помощи технических средств – калькуляторов.

Еще одна проблема современных учащихся, которая напрямую связана с вычислительной культурой, – нерациональность вычислений. Нужно обучать школьников не только выбирать и осуществлять рациональный путь выполнения упражнений и решения задачи, но и рационально записывать то или иное решение.

Из выше сказанного следует, что существует необходимость более тщательного рассмотрения этого раздела частной методики преподавания математики. Возникает потребность в ознакомлении учащихся с дополнительными приемами устных и письменных вычислений, которые позволили бы значительно сократить время, потраченное на вычисления и запись решения, и избежать использования различных вычислительных средств.

Таким образом, цель выпускной квалификационной работы: разработать методику повышения вычислительной культуры учащихся средствами использования приемов быстрого счета.

Для реализации этой цели необходимо решить следующие задачи:

1) ознакомиться с проблемой изучения вычислительной культуры учащихся;

2) изучить основные особенности математических и вычислительных навыков;

3) рассмотреть различные приемы быстрого счета как способа решения изучаемой проблемы;

4) рассмотреть применение их на уроках и внеклассных занятиях по математике;

5) разработать методическое пособие «Упражнения для быстрого счета», которое поможет учителям в проведении устного счета на уроках математики;

6) проверить эффективность предложенной методики в опытном преподавании.

Объектом исследования является процесс обучения математике в основной школе. Предмет исследования – формирование и развитие вычислительной культуры учащихся средствами системы упражнений для быстрого счета.

В ходе анализа методической литературы была сформулирована гипотеза исследования: использование приемов быстрого счета на уроках и внеклассных занятиях по математике позволит повысить вычислительную культуру учащихся.

При реализации поставленной цели и доказательстве предложенной гипотезы мы использовали следующие методы исследования: беседы с учителями, анализ психолого-педагогической и методической литературы, наблюдение, сравнительный анализ, опытное преподавание.

Работа состоит из введения, двух глав, раскрывающих основное содержание, заключения и библиографического списка. Работа также содержит приложение в форме учебно-методического пособия для обучения школьников приемам быстрого счета.

1. Требования к вычислительным умениям
и навыкам учащихся

Требования к вычислительным умениям и навыкам

О наличии у учащихся вычислительной культуры можно судить по их умению производить устные и письменные вычисления, рационально организовывать ход вычислений, убеждаться в правильности полученных результатов.

В зависимости от сложности задания на практике используются три вида вычислений: письменное, устное и письменное с промежуточными устными вычислениями.

Качество вычислительных умений определяется знанием правил и алгоритмов вычислений. Поэтому степень овладения вычислительными умениями зависит от четкости сформулированного правила и от понимания принципа его использования. Умение формируется в процессе выполнения целенаправленной системы упражнений. Очень важно владение некоторыми вычислительными умениями доводить до навыка.

Вычислительные навыки отличаются от умений тем, что выполняются почти бесконтрольно. Такая степень овладения умениями достигается в условиях целенаправленного их формирования. Образование вычислительных навыков ускоряется, если учащемуся понятен процесс вычислений и их особенности [3].

При обучении вычислениям и совершенствовании техники счета необходимо отчетливо представлять, какие умения и навыки у учащихся необходимо сформировать. Перечислим наиболее важные из них.

В письменных вычислениях данные числа, знаки арифметических действий, промежуточные и окончательные результаты записываются. Поскольку качество записей оказывает существенное влияние на успех вычисления, то учащимся необходимо владеть следующими навыками:

· отчетливо писать математические символы (цифры, знаки препинания, знаки арифметических действий);

· цифры и знаки располагать строго в соответствии с правилами арифметических действий;

· безошибочно применять таблицы сложения и умножения натуральных чисел.

При устных вычислениях надо помнить данные числа и законы действий над ними. При этом формирование навыков устных вычислений связано с выработкой навыка запоминания чисел, выявления особенностей отдельных чисел.

Правила и приемы вычислений не зависят от того, выполняются они письменно или устно. Однако владение навыками устных вычислений представляет большую ценность не только потому, что в быту ими пользуются чаще, чем письменными выкладками, но и потому, что они ускоряют письменные вычисления, позволяют усовершенствовать их. Наличие у учащихся навыков устного счета влияет на степень отработки у них рациональных и безошибочных вычислительных умений. Например, без навыков устного использования таблиц сложения и умножения невозможно в совершенстве овладеть умениями в выполнении арифметических действий.

Для того чтобы овладеть умениями, предусмотренными программой, учащемуся достаточно уметь устно:

· складывать и умножать однозначные числа;

· прибавлять к двузначному числу однозначное;

· вычитать из однозначного или двузначного числа однозначное (преимущественно из числа, меньшего 20);

· складывать несколько однозначных чисел;

· складывать и вычитать двузначные числа;

· делить однозначное или двузначное число на однозначное нацело или с остатком;

· производить действия (на основе знаний правил) с дробными числами.

Как в письменных, так и в устных вычислениях используются разнообразные правила и приемы. Умения в применении правил арифметических действий с многозначными числами, и учащиеся приобретают в начальной школе. Поэтому уровень, вычислительных навыков определяется систематичностью закрепления ранее усвоенных приемов вычислений и приобретением новых в связи с изучаемым материалом.

В 1–4 классах учащиеся обучаются выполнению арифметических действий над натуральными числами. При этом должны быть выработаны прочные навыки письменного сложения, вычитания и умножения двух-трехзначных чисел, а также деления чисел на одно- и двузначное число, что предполагает знание наизусть таблиц сложения и умножения однозначных чисел. Формирование навыков письменных вычислений, а в простейших случаях, и устных, следует довести до уровня, обеспечивающего беглое и безошибочное выполнение вычислений [6].

В 5–6 классах учащиеся овладевают навыками вычисления с натуральными и целыми числами, с обыкновенными и десятичными дробями. При этом алгоритмы вычислений с двух-трехзначными числами должны быть отработаны с учащимися до автоматизма; учащиеся должны свободно производить в уме арифметические действия в пределах сложности примеров и умножение двузначного числа на однозначное, на сложение двух дробей в простейших случаях. Все вычисления должны производиться достаточно бегло; их включение в выполнение более сложных вычислений не должно затруднять учащихся [6].

В 7–9 классах обобщаются и систематизируются сведения о действительных числах, развиваются и закрепляются вычислительные навыки. При этом не следует ослаблять внимание к поддержанию достаточно высокого уровня техники вычислений и повышению уровня вычислительной культуры учащихся (рационализация вычислений, их организация, применение приближенных вычислений). Эта задача должна решаться путем последовательного увеличения доли вычислений при изучении основного материала курса. Вычислительные навыки учащихся должны получить дальнейшее развитие при изучении вопросов, связанных с приближенными вычислениями, где, помимо дальнейшей отработки вычислительных алгоритмов, должны быть сформированы навыки прикидки и оценки результатов вычислений. По мере усвоения учащимися вычислительных алгоритмов и расширения объема сведений о числовых функциях существенно увеличивается объем и сложность вычислительных работ, что требует привлечения таблиц и математических инструментов (калькулятора) [6].

Вычислительным навыкам, как и любым другим, необходимо учить. Качество вычислительных умений и навыков определяется знанием правил и алгоритмов вычислений. Поэтому степень овладения вычислительными умениями зависит от четкости сформулированного алгоритма и от понимания принципа его использования. Очень важно владение некоторыми вычислительными умениями доводить до навыка. Что нужно сделать для этого учителю?

1. Ознакомить учащихся с принципом работы того или иного нового для них вычислительного алгоритма.

2. Провести работу по отработке отдельных операций, входящих в новый алгоритм. Для формирования навыка выполнения данного алгоритма недостаточно отдельных упражнений, необходима тщательно продуманная их система, в которой должна соблюдаться последовательность упражнений с постепенным их усложнением. Однако следует предостеречь от излишнего числа однообразных упражнений в системе. Упражнения по формированию навыков должны быть достаточно разнообразными как по содержанию, так и по форме, лишь в этом случае достигается прочность навыков.

3. Провести работу по закреплению алгоритма – использовать его применение во всех стандартных и нестандартных ситуациях. Это немаловажно, так как уровень вычислительных навыков определяется систематичностью закрепления ранее усвоенных приемов вычислений и приобретением новых в связи с изучаемым материалом. Кроме того, формируемые навыки в выполнении вычислений и тождественных преобразований должны входить в ранее сформированную систему знаний, умений и навыков учащихся как составная часть. Поэтому после нескольких упражнений в формировании нового вычислительного умения или навыка полезно для достижения этой цели выполнять упражнения, связывающие изучаемое с ранее приобретенными умениями и навыками.

4. И, конечно же, необходимо провести проверку по усвоению алгоритма учащимися. Этому могут помочь проведение самостоятельных работ и наблюдения учителя за работой учащихся в классе. Анализ письменных и устных работ учащихся дает возможность установить, как усвоен данный материал, какие общие и наиболее характерные ошибки допущены при проведении вычислений, кто из учащихся и что именно не усвоил и как ликвидировать выявленные пробелы.

Вычислительные навыки и умения можно считать сформированными только в том случае, если учащиеся умеют с достаточной беглостью выполнять математические действия с натуральными числами, десятичными и обыкновенными дробями, рациональными числами, производить тождественные преобразования различных числовых выражений и приближенные вычисления, рационально организовывать ход вычислений, а также убеждать в правильности полученных результатов.

На каких же этапах урока и внеклассных мероприятий можно обучать вычислительным навыкам? На уроках можно отводить 5–10 минут, в течение которых учащиеся знакомятся с каким-либо алгоритмом и закрепляют его решением примеров. Пятиминутки «устного счета» так же могут быть использованы для формирования и отработки вычислительного навыка. На этапе актуализации знаний можно провести проверку знаний того или иного вычислительного алгоритма. А на внеклассных мероприятиях можно ввести специальное отделение, в котором учащиеся, хорошо владеющие вычислительными алгоритмами, с успехом выступают перед одноклассниками. Также можно использовать различные игровые приемы (конкурсы, состязания) для изучения, закрепления, проверки знания вычислительных алгоритмов.

Таким образом, вычислительные навыки нужны и при изучении программного материала в школе, и в повседневной жизни. Кроме того, они окажутся полезными для прикидки ожидаемого результата не только в учебной деятельности, но и в жизни. Именно поэтому учить учащихся быстро, правильно и рационально считать в школе необходимо и не только на уроках, но и на внеклассных занятиях по математике.

Дроби

1. Умножение целого числа на смешанное. Умножение целого числа на смешанное число может быть выполнено по правилу умножения числа на сумму, так как смешанное число есть сумма целого числа и дроби. Поясним это на числовом примере:

1) .

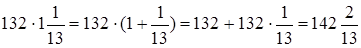Но при умножении целого числа на смешанное число можно обратить смешанное число в неправильную дробь, затем умножить целое число на числитель неправильной дроби, полученное произведение сделать числителем искомого произведения, знаменатель же произведения оставить знаменатель множителя:

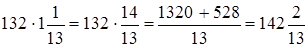Как видим, первый способ проще и дает возможность быстрее производить умножение.

2) .

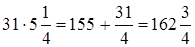Преимущество первого способа перед вторым в данном примере очевидно. Но могут быть случаи, когда проще и быстрее можно решить пример вторым способом:

3) .

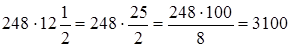Таким образом, при умножении целого числа на смешанное число надо внимательно рассмотреть пример и применить тот способ, который в данном случае быстрее ведет к цели.

2. Деление смешанного числа на целое. Смешанное число можно рассматривать как сумму двух чисел. Следовательно, деление смешанного числа на целое есть деление суммы двух чисел на число. Чтобы разделить сумму чисел на число, достаточно разделить на это число каждое из слагаемых, и сложить полученные результаты.

Мы знаем, что все основные законы арифметических действий, установленные для натуральных чисел, сохраняют свою силу и для дробных чисел:

1) 348 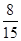: 4 = (348 + 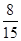): 4 = 348: 4 + 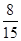: 4 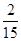= 87 + = 87 .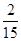

Как видим, этот способ гораздо легче (он дает возможность быстрее производить вычисления), чем обычный способ деления смешанного числа на целое с образованием смешанного числа в неправильную дробь.

2) 252 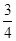: 12 = (252 + 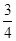): 12 = 252: 12 + 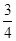: 12 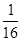= 21 + = 21 .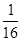

3. Умножение и деление целого числа на дробь, которая отличается от единицы на одну долю:

а) умножение

1) ;

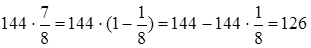2) ;

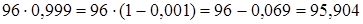б) деление

3) .

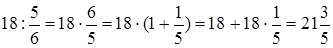Рассмотрим пример деления целого числа на дробь, причем дробь отличается от единицы на две и более долей:

1) .

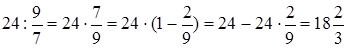Как мы видим, данный способ дает возможность быстрее умножать и делить целое число на дробь, чем обычный способ, а поэтому следует разобранный способ использовать при умножении или делении целого числа на дробь.

Проценты

Устное нахождение процентов числа и числа по данным его процентам

Устное нахождение 5%, 25%; 12,5% числа и т.п., а также числа по данным его процентам основано на умножении и делении на дроби 0,05; 0,25; 0,125 и т.п.

а) Нахождение процента от числа.

1) Найти 25% от 468.

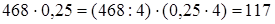. Но можно заменить 25% и обыкновенной дробью. Этот пример можно решить так: .

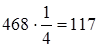2) Найти 12,5% от 728.

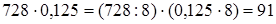Можно 12,5% заменить обыкновенной дробью: .

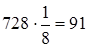б) Нахождение числа по данным его процентам.

Найти число, если 5% его равны 492.

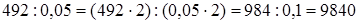Как видим, способ замены процентов обыкновенной дробью иногда дает возможность быстрее производить вычисления, чем умножением на десятичную дробь.

Нахождение квадратов числа

1. Таблица квадратов целых чисел от 1 до 25 включительно.

На основании того, что суммы последовательных нечетных чисел:
1 + 3 = 4; 1 + 3 + 5 = 9; 1 + 3 + 5 + 7 = 16 и т.д. – представляют собой ряд квадратов, разработаны следующие способы составления таблицы квадратов.

а) Первый способ составления таблицы квадратов чисел от 1 до 25.

Числа		Квадраты чисел
целые	нечетные
1	1	1
2	3	4
3	5	9
4	7	16
5	9	25
6	11	36
7	13	49
8	15	64
9	17	81
10	19	100
11	21	121
12	23	144
13	25	169
14	27	196
15	29	225
16	31	256
17	33	289
18	35	324
19	37	361
20	39	400
21	41	441
22	43	484
23	45	529
24	47	576
25	49	625

В первой колонке написан ряд последовательных целых чисел, начиная с единицы. Во второй колонке написан ряд нечетных чисел, начиная с 1. Третья колонка содержит ряд квадратов целых чисел, указанных в первой колонке.

Таблица составляется следующим образом: в первой строке пишут число 1; этот первый квадрат прибавляют к нечетному числу следующей строчки из второй колонки и получают второй квадрат 4. Прибавляя 4 к третьему нечетному числу (5) из второй колонки, получаем 3², т.е. 9. Вообще, квадрат числа есть сумма нечетного числа, которое стоит в одной с ним строке и непосредственно предшествующего квадрата. В одной и той же строке слева направо расположены: 1) целое число; 2) нечетное число, для которого это целое число служит номером в ряде нечетных чисел; 3) квадрат целого числа.

б) Второй способ составления таблицы квадратов чисел от 1 до 25.

В первой вертикальной колонке пишутся по порядку целые числа, начиная с единицы. Во второй колонке пишется ряд нечетных чисел, начиная с 3. В третьей колонке, которая должна содержать ряд, квадратов всех целых чисел, пишется сначала квадрат 1, т.е. единица. Чтобы получить каждый из следующих квадратов, прибавляют к последнему числу третьей колонки то нечетное число, которое стоит слева от него, во второй колонке. Каждое из чисел третьей колонки есть квадрат соответствующего числа первой колонки.

Числа		Квадраты чисел
целые	нечетные
1	3	1
2	5	4
3	7	9
4	9	16
5	11	25
6	13	36
7	15	49
8	17	64
9	19	81
10	21	100
11	23	121
12	25	144
13	27	169
14	29	196
15	31	225
16	33	256
17	35	289
18	37	324
19	39	361
20	41	400
21	43	441
22	45	484
23	47	529
24	49	576
25	51	625

Числа	Квадраты чисел
1	1
2	4
3	9
4	16
5	25
6	36
7	49
8	64
9	81
10	100
11	121
12	144
13	169
14	196
15	225
16	256
17	289
18	324
19	361
20	400
21	441
22	484
23	529
24	576
25	625

в) Третий способ составления таблицы квадратов чисел.

Квадраты чисел от 1 до 10 включительно определяем по таблице умножения: в первой колонке пишем числа, во второй – их квадраты. Чтобы получить квадрат следующего числа, к квадрату данного числа прибавляем сумму данного числа и следующего числа. Рассмотрим на числовых примерах.

1) квадрат числа 11 равен 100 + (10+ 11)= 121;

2) квадрат числа 12 равен 121 + (11 + 12) = 144 и т.д.

Объяснение этого способа нахождения квадрата числа следующее:

( k + 1)² = k ² + 2 k • 1 + 1² = k ² + [ k + ( k + 1)].

3) 75² = 5625. 76² = (75 +1)² = 75² + [75 + (75 + 1)] = 75² +
+ (75 + 76) = 5625 + 151 = 5776. Получаем 76² = 5776.

2. Возведение в квадрат и умножение с помощью формул сокращенного умножения.

а) Вычисления по формуле .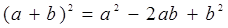

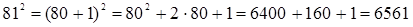б) Вычисления по формуле .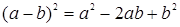

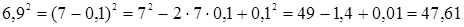в) Особенно полезным оказывается применение в устных вычислениях формулы .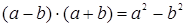

1) .

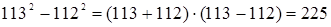2) .

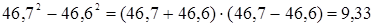3. Устное возведение в квадрат смешанных чисел. Случаи возведения в степень смешанного числа по формулам сокращенного умножения.

а) Квадрат смешанного числа с дробью 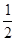. Чтобы возвести в квадрат смешанное число с дробью 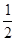, достаточно умножить целую часть числа на число, единицей большее, и к произведению приписать .

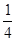Дано: число k + 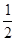, где k – целое. Доказать: ( k + 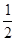)² = k ( k + 1) + .

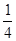Доказательство: ( k + 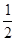)² = k ² + 2 • k • 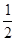+ 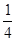= k ² + k + 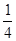= k ( k + 1) + .

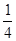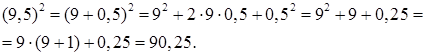
б) Квадрат смешанного числа с дробью 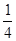. Чтобы возвести в квадрат смешанное число с дробью 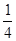, достаточно возвести в квадрат целую часть этого числа, затем прибавить ее половину и, наконец, к полученной сумме прибавить 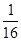, если целая часть – четное число. Если же целая часть – нечетное число, то к квадрату целой части прибавляется половина числа, на единицу меньшего данной целой части смешанного числа, и к сумме прибавляется .

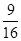1) Дано: число k + 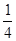, где k – четное число. Доказать: ( k + 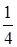)² = k ² + + .

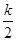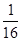Доказательство: ( k + 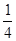)² = k ² + 2 • k • 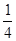+ 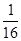= k ² + + .

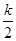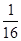2) Дано: число k + 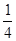, где k – нечетное число. Доказать: ( k + 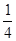)² = k ² + + 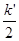+ 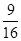(в данном случае k ’ на единицу меньше числа k).

Доказательство: k = k ’ + 1, следовательно,

( k + 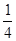)² = k ² + 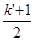+ 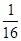= k ² + 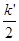+ + 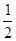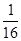= k ² + + .

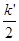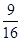1) k – четное число

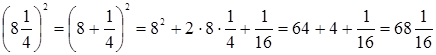2) k – нечетное число

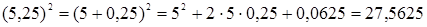Сложение

1. Замена нескольких слагаемых их суммой (сочетательный закон).

1) 187 + 247 + 153 = 187 + (247 + 153) (группу слагаемых заключаем в скобки и складываем, на основании сочетательного закона) = 187 + 400 = 587.

2) 16,53 + 4,47 + 9,84 = (16,53 + 4,47) + 9,84 = 21 + 9,84 = 30,84.

2. Перестановка слагаемых (переместительный закон).

1) 238 + 487 + 362 = 238 + 362 + 487 (делаем перестановку слагаемых, применяя переместительный закон, чтобы получить круглое число при сложении) = (238 + 362) + 487 (группу слагаемых заключаем в скобки и складываем на основании закона сочетательности) = 600 + 487 = 1087.

2) 3,57 + 4,68 + 6,43 = 3,57 + 6,43 + 4,68 = (3,57 + 6,43) + 4,68 = 14,68.

3) 235 + 47 + 7 + 265 + 3 + 53 = 235 + 265 + 47 + 53 + 7 + 3 = (235 + 265) + (47 + 53) + (7 + 3) = 500 + 100 + 10 = 610.

4) 8,3 + 3,85 + 9,7 + 5,15 + 2,25 = 8,3 + 9,7 + 3,85 + 5,15 + 2,25 = (8,3 + 9,7) + (3,85 + 5,15) + 2,25 = 18 + 9 + 2,25 = 29,25.

Близок к указанному способу прием перемещения единиц. Например:

1) 1347 + 2235 = 1347 + 33 + 2202 = (1347 + 33) + 2202 = 1380 + 2202 = 3582.

2) 13,98 + 7,12 = 13,98 + 0,02 + 7,1 = (13,98 + 0,02) + + 7,1 = 14 + 7,1 = 21,1.

Для упрощения вычислений мы разбивали слагаемое на части с целью привести вычисления к сложению целых чисел или круглых десятков, применяя сочетательный закон.

3. Прибавление суммы к числу.

1) 384 + (416 + 548) = 384 + 416 + 548 (на основании следствия сочетательного закона) = (384 + 416) + 548 (сочетательный закон) = 800 + 548 (правило порядка действий) = 1348.

Итак, правило прибавления суммы можно сформулировать следующим образом: чтобы прибавить к числу сумму, достаточно прибавить к нему одно за другим все слагаемые.

2) 3,64 + (4,36 + 9,78) = 3,64 + 4,36 + 9,78 = (3,64 + 4,36) + 9,78 = 8 + 9,78.

4. Прибавление числа к сумме.

1) (337 + 488) + 663 =663 + (337 + 488) (переместительный закон) = 663+ + 337 + 488 (правило прибавления суммы) = (663 + 337) + 488 (сочетательный закон) = 1000 + 488 = 1488.

Примененное здесь свойство сложения формулируется так: чтобы к сумме чисел прибавить число, достаточно прибавить его к одному из слагаемых.

2) (4,55 + 6,89) + 5,45 = (4,55 + 5.45) + 6,89 = 10 + 6,89 = 16,89.

5. Прибавление к сумме другой суммы.

1) (327 + 684 + 168) +(473 + 316 + 132) = (327 +684 + 168) + 473 + 316 + + 132 = 327 + 684 + 168 + 473 + 316 + 132 (правило прибавления суммы к числу) = 327 + 473 + 684 +316 +168 + 132 (переместительный закон) = (327 + 473) + + (684 + 316) + (168 + 132) (сочетательный закон) = 800 + 1000 + 300 = 2100.

2) (12,24 + 27,58) + (37,76 + 2,42) = (12,24 + 37,76) + (27,58 + 2,42) = 50 + 30 = 80.

Сложение и вычитание

1. Перестановка членов ряда сложений и вычитаний (перестановка членов алгебраической суммы).

1‑й случай.

1) 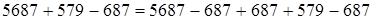(если из какого-либо числа вычесть и затем прибавить одно и то же число, то данное число останется без изменения) 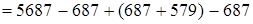(сочетательность сложения) 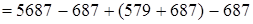(переместительность сложения) 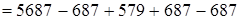(следствие сочетательного закона) 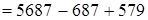(если к какому-либо числу прибавить и затем вычесть одно и то же число, то данное число останется без изменения) = 5000 + 579 (порядок действий) = 5579. Итак, .

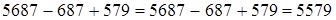Результат ряда сложений и вычитаний не меняется от перемены порядка членов ряда (при этом каждый член ряда остается в его прежней роли слагаемого или вычитаемого).

При введении отрицательных чисел, обоснование решения подобного примера весьма просто: для членов алгебраической суммы справедливы переместительный и сочетательный законы сложения.

2‑й случай.

2) 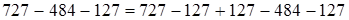(если из какого-либо числа вычесть и затем прибавить одно и то же число, то данное число не изменится) 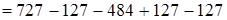(первый случай переместительности членов ряда сложений и вычитаний) 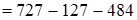(если к какому-либо числу прибавить и затем вычесть одно и то же число, то данное число не изменится) 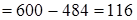. Итак, .

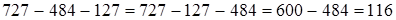2. Прибавление разности к числу (первый случай сочетательности членов ряда сложений и вычитаний).

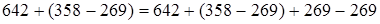(если к какому-нибудь числу прибавить и затем вычесть одно и то же число, то данное число не изменится) 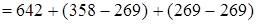(сочетательный закон) 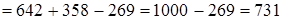(производим сложение и вычитание). Итак, .

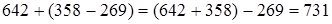При решении подобных примеров применяется следующее правило: чтобы к числу прибавить разность, достаточно прибавить к нему уменьшаемое и из полученной суммы вычесть вычитаемое.

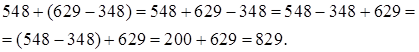
В этом случае правило может быть сформулировано так: чтобы к числу прибавить разность, достаточно из данного числа вычесть вычитаемое и к полученному числу прибавить уменьшаемое.

3. Вычитание из числа суммы (второй случай сочетательности членов ряда сложений и вычитаний).

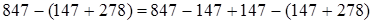(если из какого-нибудь числа вычесть и затем прибавить одно и то же число, то данное число не изменится) 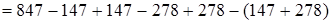(на том же основании) = 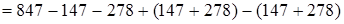(переместительный и сочетательный законы) 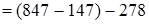(если к какому-нибудь числу прибавить и затем вычесть одно и то же число, то данное число не изменится) 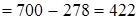. Итак, .

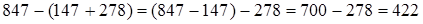Чтобы из числа вычесть сумму, достаточно вычесть из него одно за другим каждое слагаемое.

4. Вычитание из числа разности (третий случай сочетательности членов ряда сложений и вычитаний).

1) 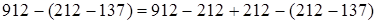(если из какого-нибудь числа вычесть и затем прибавить одно и то же число, то данное число останется без изменения) 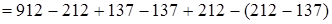(на том же основании) 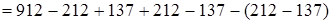(переместительность членов ряда сложений и вычитаний) 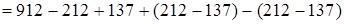(сочетательность членов ряда сложений и вычитаний) 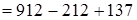(если к какому-нибудь числу прибавить и затем вычесть одно и то же число, то данное число не изменится) = 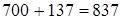. Итак, .

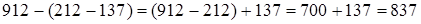Чтобы из числа вычесть разность, достаточно вычесть уменьшаемое и затем прибавить вычитаемое.

2) 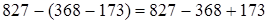(вычитание из числа разности) 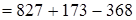(переместительность членов ряда сложений и вычитаний) 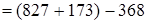(сочетательность суммы) 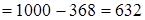(выполняем сложение и вычитание полученных чисел).

Таким образом, чтобы из числа вычесть разность, достаточно прибавить к нему вычитаемое и затем отнять уменьшаемое. Так как в математике нельзя из меньшего числа вычитать большее, то в случае, когда уменьшаемое больше числа, из которого вычитается разность, применить можно лишь второе из этих правил. Во всех остальных случаях выбираем то правило вычитания из числа разности, которое дает более быстрые и простые вычисления.

5. Вычитание из суммы числа.

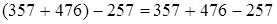(порядок действий) 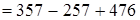(переместительность ряда сложений и вычитаний) 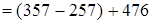(сочетательность ряда сложений и вычитаний) = 100 + 476 = 576. Итак, .

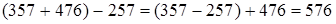Чтобы из суммы чисел вычесть какое-нибудь число, достаточно вычесть его из одного слагаемого.

6. Вычитание из разности числа.

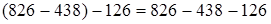(порядок действий) 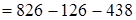(переместительность) 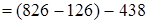(сочетательность) 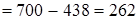. Чтобы из разности вычесть число, достаточно вычесть его из уменьшаемого и из полученного числа вычесть вычитаемое.

Здесь применено следующее правило: чтобы из разности вычесть число, достаточно прибавить его к вычитаемому и полученное число вычесть из уменьшаемого.

7. Вычитание из суммы другой суммы.

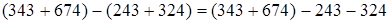(вычитание суммы из числа) 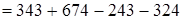(порядок действий) 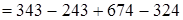(переместительность) 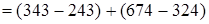(сочетательность) =
= 100 + 350 (порядок действий) = 450.

Чтобы из суммы чисел вычесть другую сумму, можно из отдельных слагаемых первой суммы вычитать меньшие или равные им слагаемые второй суммы.

8. Вычитание из разности другой разности.

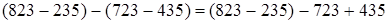(вычитание разности из числа) 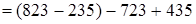(порядок действий) 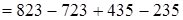переместительность) 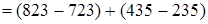(сочетательность) = 100 + 200 = 300. Итак, .

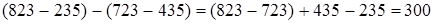Чтобы из разности чисел вычесть другую разность, достаточно из уменьшаемого первой разности вычесть уменьшаемое второй, а из вычитаемого второй вычесть вычитаемое первой и результаты этих вычитаний сложить.

Замечание 1. В рассмотренных примерах на действия с положительными числами (и нулем) и сформулированных к ним правилах всюду подразумевалась выполнимость вычитания, т.е. предполагалось наличие разности, выражаемой неотрицательным числом.

Замечание 2. Обоснование всех описанных выше приемов вытекает из свойств алгебраической суммы.

Умножение

1. Замена нескольких сомножителей их произведением (сочетательный закон умножения).

1) 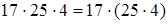(сочетательность умножения) = 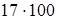= 1700.

Чтобы перемножить несколько чисел, достаточно отдельные сомножители соединить в группы, произвести умножение по группам, а затем перемножить полученные произведения.

2) .

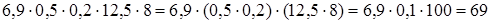2. Перестановка сомножителей (переместительный и сочетательный законы умножения).

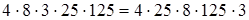(переместительность умножения) = 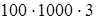(сочетательность умножения) = 300 000.

Чтобы перемножить несколько чисел, можно поменять местами отдельные сомножители, соединить их в группы, затем произвести умножение по группам и перемножить полученные произведения.

3. Умножение произведения на число.

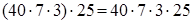(порядок действий) = 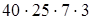(переместительность умножения) = 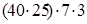(сочетательность умножения) = .

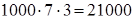Чтобы умножить произведение нескольких чисел на какое-либо число, достаточно один из сомножителей умножить на это число и полученное произведение последовательно умножить на другие сомножители.

4. Умножение числа на произведение.

1) 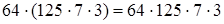(следствие сочетательного закона) = 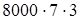(сочетательность умножения) = 168000.

Чтобы умножить число на произведение нескольких чисел, достаточно умножить это число на первый сомножитель, полученное произведение – на второй, затем новое произведение – на третий и т.д. до конца.

К указанному способу близок прием умножения посредством замены множителя соответствующим произведением (иногда это называют последовательным умножением).

2) .

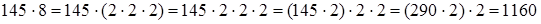5. Умножение произведения на произведение.

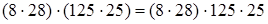(умножение числа на произведение) = 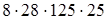(порядок действий) = 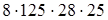(переместительность) 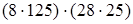(сочетательность) = .

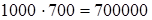Здесь применено следующее правило: чтобы умножить произведение нескольких чисел на другое произведение, достаточно последовательно перемножить все сомножители обоих произведений.

Умножение и деление

1. Перестановка членов ряда умножений и делений (переместительность ряда умножений и делений).

1) 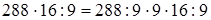(если данное число разделить на какое-нибудь число и затем полученное частное умножить на это же число, то данное число останется без изменения) = 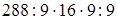(переместительность умножения) = 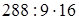(если данное число умножить на какое-нибудь число, отличное от 0, и затем полученное произведение разделить на это же число, то данное число останется без изменения) =512 (правило порядка действий: действия одной и той же ступени (при отсутствии скобок) выполняются в том порядке, в каком они записаны).

2) 486: 9: 2 = 486: 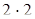: 9: 2 (если данное число разделить на какое-нибудь число и затем полученное частное умножить на это же число, то данное число останется без изменения) = 486: 2: 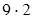: 2 (переместительность членов ряда умножений и делений) = 486: 2: 9 (если данное число умножить на какое-нибудь число (не равное нулю) и затем полученное произведение разделить на это число, то данное число останется без изменения) = 243: 9 = 27.

Результат ряда умножений и делений не меняется от перемены порядка членов данного ряда (разумеется, что каждый член ряда остается в своей прежней роли, иначе говоря, переносится на другое место вместе с написанным перед ним знаком действия).

2. Умножение числа на частное.

1) 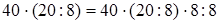(если данное число умножить на какое-нибудь число (не равное нулю) и затем полученное произведение разделить на это же число, то данное число остаются без изменения) = 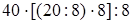(сочетательность умножения) = 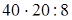(если данное число разделить, на какое-нибудь число и затем полученное частное умножить на это же число, то данное число останется без изменения) = 800: 8 = 100 (порядок действий). Итак, .

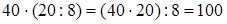Чтобы умножить число на частное, можно умножить его на делимое, и полученное произведение разделить на делитель.

2) .

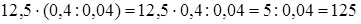3. Деление числа на произведение.

1) 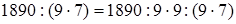(если данное число разделить на какое-нибудь число и полученное частное умножить на то же самое число, то данное число останется без изменения) = 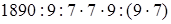(объяснение то же) = 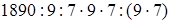(переместительность умножения) = 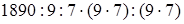(сочетательность умножения) = 1890: 9: 7 (если данное число умножить на какое-нибудь число (не равное нулю) и затем полученное произведение разделить на это же число, то данное число останется без изменения) = 210: 7 = 30 (порядок действий).

Чтобы разделить число на произведение нескольких чисел, достаточно разделить его на первый сомножитель, полученное частное – на второй, новое частное – на третий и т.д. до конца.

2) 8,16: ( 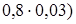= 8,16: 0,8: 0,03 = 10,2: 0,03=340.

К указанным способам близки по обоснованию приема следующие: разложение делителя на множители и замена нескольких делителей их произведением.

3) 1890: 54 = 1890: ( 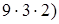= (1890: 9): 3: 2 = (210: 3): 2 = 70: 2 = 35.

4) 2800: 25: 8 = 2800: ( 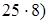= 2800: 200 = 14.

4. Деление произведения на число.

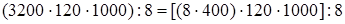(так как 3200 = 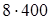) = 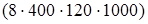: 8 (порядок действий) = 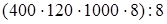(переместительность умножения) = 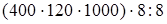(сочетательность умножения) = 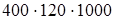(если данное число умножить на какое-нибудь число (не равное нулю) и затем полученное произведение разделить на это же число, то данное число останется без изменения) = 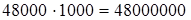(порядок действий).

Чтобы разделить произведение нескольких чисел на какое-нибудь число, достаточно разделить на это число один из сомножителей, оставив другие без изменения.

5. Деление произведения нескольких чисел на другое произведение.

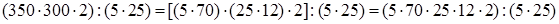
(следствие сочетательного закона) = 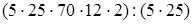(переместительность умножения 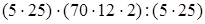(сочетательность умножения) = 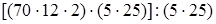(переместительность) = 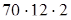(деление произведения на число) = 1680 (умножаем полученные числа).

Чтобы разделить произведение нескольких чисел на другое произведение, все сомножители которого входят в состав первого произведения, достаточно разделить, каждый из сомножителей первого произведения на соответствующий сомножитель второго произведения, а затем полученные частные и оставшиеся сомножители перемножить.

6. Деление числа на частное.

3200: (800: 32) = 3200: 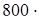800: (800: 32) (если данное число разделить на какое-нибудь число, а затем полученное частное умножить на это же число, то данное число останется без изменения)
= 3200: 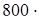32: 32 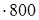: (800: 32) (если данное число умножить на какое-либо число (не равное нулю), а затем полученное произведение разделить на это же число, то данное число останется без изменения)
= 3200: 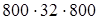: 32: (800: 32) (переместительность ряда умножений и делений) = 3200: 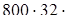(800: 32): (800: 32) (сочетательность ряда умножения и деления) = 3200: 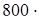32 (если данное число умножить на какое-нибудь число (не равное нулю), а затем полученное произведение разделить на это же число, то данное число останется без изменения) = 4 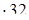= 128 (делим и умножаем полученные числа).

Чтобы разделить число на частное, достаточно разделить его на делимое, а затем полученное частное умножить на делитель.

Сложение и вычитание

1. Округление одного или нескольких слагаемых.

Этот прием основан на изменении суммы при изменении слагаемых.

а) Если одно из слагаемых увеличить (или уменьшить) на несколько единиц (или долей), а другое слагаемое оставить без изменения, то сумма увеличится (или уменьшится) на столько же единиц (или долей). Округляя слагаемое, мы увеличиваем (или уменьшаем) его, а следовательно, и сумму на несколько единиц (или долей). Чтобы сумма не изменилась, надо уменьшить (или увеличить) ее на столько же единиц (или долей).

1199 + 406 = (1200 + 406) 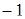= 1605.

б) Если одно из слагаемых увеличить (или уменьшить) на несколько единиц (или долей), другое слагаемое уменьшить (или увеличить) на столько же единиц (или долей), а остальные слагаемые оставить без изменения, то сумма не изменится. Перемещаем несколько единиц (долей) из одного слагаемого в другое, сумма не изменяется.

994 + 196 = 994 + 190 + 6 = (994 + 6) + 190 = 1000 + 190 = 1190.

В том случае, когда одно из слагаемых близко к разрядной единице (на несколько единиц больше или меньше) или близко к целому числу (на несколько долей больше или меньше его), удобнее заменить его разрядной единицей или целым числом, а в полученный от сложения результат внести необходимую поправку.

2. Округление уменьшаемого или вычитаемого.

Этот прием основан на изменении разности от изменения уменьшаемого или вычитаемого.

а) Если уменьшаемое увеличить или уменьшить на несколько единиц (или долей), то разность соответственно увеличится или уменьшится на столько же единиц (или долей). Округляя уменьшаемое, мы увеличиваем или уменьшаем его на несколько единиц (или долей), следовательно, и разность увеличивается или уменьшается настолько же единиц (или долей). Чтобы разность не изменилась, надо ее уменьшить или увеличить настолько же единиц (или долей).

1) .

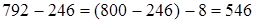Уменьшаемое увеличено на несколько единиц, разность, записанная в скобках, должна быть уменьшена на столько же единиц.

2) .

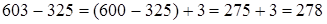Уменьшаемое уменьшено на несколько единиц; записанная в скобках разность должна быть увеличена на столько же единиц.

б) Если вычитаемое увеличить или уменьшить на несколько единиц (или долей), то разность соответственно уменьшится или увеличится на столько же единиц (или долей). Округляя вычитаемое, мы увеличиваем или уменьшаем его, а следовательно, разность уменьшается или увеличивается на несколько единиц (или долей). Чтобы разность не изменилась, надо ее увеличить или уменьшить на столько же единиц (или долей).

1) .

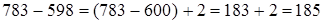Вычитаемое увеличено на несколько единиц, записанная в скобках разность должна быть увеличена на столько же единиц.

2) 7,83 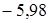= (7,83 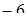) + 0,02 = 1,83 + 0,02 = 1,85.

Вычитаемое увеличено на несколько долей; разность, записанная и скобках, должна быть увеличена на столько же долей.

3) 910 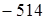= (910 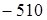) 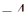= 396.

Вычитаемое уменьшено на несколько единиц, записанная в скобках разность должна быть уменьшена на столько же единиц.

Итак:

1) При округлении уменьшаемого:

а) если уменьшаемое увеличено, разность надо уменьшить;

б) если уменьшаемое уменьшено, разность надо увеличить.

2) При округлении вычитаемого:

а) если вычитаемое увеличено, то и разность надо увеличить;

б) если вычитаемое уменьшено, то и разность надо уменьшить.

Выгоднее округлять вычитаемое, так как разрядное или целое число легко вычитается из любого числа.

Если уменьшаемое и вычитаемое увеличить или уменьшить на одинаковое число единиц (долей), то разность не изменится.

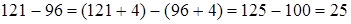В данных примерах уменьшаемое и вычитаемое увеличены на одно и то же число, разность не изменилась.

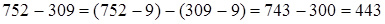В данных примерах уменьшаемое и вычитаемое уменьшены на одно и то же число, разность не изменилась.

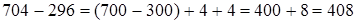В данных примерах, округляя уменьшаемое, мы уменьшали разность на несколько единиц (долей); округляя вычитаемое, мы также уменьшали разность на несколько единиц (долей). Следовательно, «округленная» разность должна быть увеличена на такую сумму единиц (долей), на какую мы уменьшили уменьшаемое и увеличили вычитаемое.

3. Арифметическое дополнение. Замена сложения вычитанием и вычитания сложением.

а) Арифметическим дополнением числа называется число, которое нужно прибавить к данному числу, чтобы получить единицу непосредственно высшего разряда. Дополнением числа 9247 будет число, которое надо прибавить к 9247, чтобы получить 10000. Поэтому, чтобы найти дополнение какого-либо числа, надо вычесть это число из единицы со столькими нулями, сколько в числе цифр: 10000 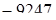= 753. Таким образом, для получения дополнений надо все цифры данного числа вычитать из 9, за исключением последней справа значащей цифры, которую вычитать из 10. Если находят дополнение числа с нулями на конце, то приписывают столько нулей, сколько их было за последней значащей цифрой.

В замене сложения вычитанием первое слагаемое вычитаем из ближайшего разрядного числа (ищем его дополнение до разрядного числа), полученная разность вычитается из второго слагаемого и результат складывается с разрядным числом.

89 + 47:

1) 100 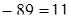; 2) 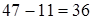; 3) 100 + 36= 136.

Способ замены сложения вычитанием удобен в том случае, когда дополнение первого слагаемого до разрядного числа легко вычитается из второго слагаемого.

б) В замене вычитания сложением находим дополнение вычитаемого до ближайшего разрядного числа и к нему прибавляем разность между уменьшаемым и этим разрядным числом.

112 – 67:

1) 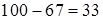; 2) 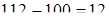; 3) 12 + 33 = 45.

Этот способ удобен, когда единицы, десятки и т.д. вычитаемого больше единиц, десятков и т.д. уменьшаемого.

а) Для одновременного производства сложения и вычитания можно вместо вычитаемых взять их дополнения до одного и того же числа, изображенного единицей с нулями, найти сумму новых слагаемых, а затем ее исправить, вычтя числа, до которых взяты дополнения. 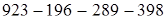. Заменим все три вычитаемых дополнением каждого до 1000 и вычтем столько тысяч, сколько взято дополнений, т.е. 3000: 923 + 804 + 711 + 602 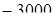= 40.

Этот способ удобен в том случае, когда цифры вычитаемых больше пяти.

б) Когда же цифры вычитаемых меньше пяти, то можно не заменять вычитаемые их дополнениями. В таком случае следует подписать числа с их знаками одно под другим.

Умножение и деление

Мы знаем, что если один из сомножителей увеличить в несколько раз, а другой уменьшить во столько же раз, то произведение не изменится. На этом свойстве основывается применение сокращенных способов умножения на 5, 25, 125 и на другие числа, представляющие собой делители числа, изображаемого единицей с нулями.

1. Умножение на 5, 50, 500 и т.д.

Умножение числа на 5, 50, 500 и т.д. заменяется умножением на 10, 100, 1000 и т.д. с последующим делением на 2 полученного произведения. Или: сначала множимое делится на 2, а потом полученное частное умножается на 10, 100, 1000 и т.д.

1) ; ;

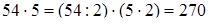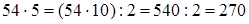2) ;

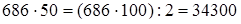3) .

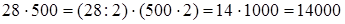2. Умножение на 25, 250, 2500 и т.д.

При умножении числа на 25, 250, 2500 и т.д. достаточно данное число умножить на 100, 1000, 10000 и т.д. и полученный результат разделить на 4. Или: сначала данное число разделить на 1, затем полученное частное умножить на 100, 1000, 10000 и т.д.

1) ;

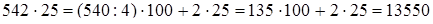2) ;

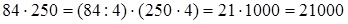3) .

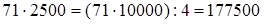3. Умножение на 125, 1250 и т.д.

При умножении числа на 125, 1250 и т.д. данное число умножают на 1000, 10000 и т.д., полученное произведение делят на 8. Или: данное число делят на 8 и полученное частное умножают на 1000, 10000 и т.д.

1) 72 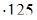= (72: 8) 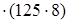= 9 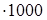= 9000, или

72 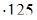= 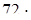(100 + 25) = 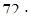100 + 72: 4 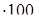= 7200 + 1800 = 9000

4. Умножение на 37.

При умножении числа на 37, если данное число кратно 3, его делят на 3 и умножают на 111.

1) .

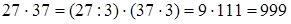Если же данное число не кратно 3, то из произведения вычитают 37 или к произведению прибавляют 37.

2) ;

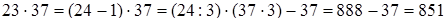3) .

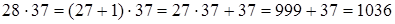Известно, что если делимое и делитель увеличить или уменьшить в одинаковое число раз, то частное не изменится. На этом свойстве основывается применение сокращенных способов деления на 5, 25, 125 и на другие числа, представляющие какую-либо часть числа, изображенного единицей с нулями.

5. Деление на 5, 50, 500 и т.д.

Деление числа на 5, 50, 500 и т.д. заменяется делением на 10, 100, 1000 и т.д. с последующим умножением на 2. Или: делимое умножается на 2 и полученное произведение делится на 10, 100, 1000 и т.д.

1) 8740: 5 = (8740: 10) 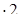= 874 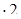= 1748;

2) 197500: 50 = (197500: 100) 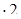= 3950;

3) 3,7: 500 = (3,7 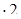): (500 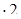) = 7,4: 1000 = 0,0074.

6. Деление на 25, 250 и т.д.

При делении числа на 25, 250 и т.д. достаточно разделить его на 100, 1000 и т.д. и полученное частное умножить на 4. Или: сначала делимое умножить на 4, а потом полученное произведение разделить на 100, 1000 и т.д.

1) 14200: 25 = (14200: 100) 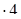= 142 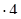= 568;

2) 14, 4: 25 = (14,4: 100) 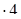= 0,144 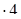= 0,576, или

14,4: 25 = (14,4 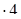): (25 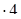) = 57,6: 100 = 0,576.

7. Деление на 125, 1250 и т.д.

При делении числа на 125, 1250 и т.д. достаточно разделить его на 1000, 10000 и т.д. и полученное частное умножить на 8. Или: сначала делимое умножить на 8, а потом полученное произведение разделить на 1000, 10000 и т.д.

1) 35000: 125 = (35000: 1000) 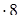= 35 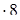= 280;

2) 32250: 125 = (32250 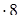): (125 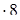) = 258000: 1000 = 258.

Содержание и анализ опытно-экспериментальной работы

Опытно-экспериментальная работа по повышению вычислительной культуры школьников была проведена в 6-а классе средней школы №51 г. Кирова.

Для эксперимента был взят общеобразовательный класс со средней успеваемостью.

В начале каждого урока ученикам предлагались карточки с заданиями на отработку одного из приемов быстрого счета (см. прилагаемое пособие). Было представлено четыре блока заданий. В первом блоке были примеры, основанные на способе группировки слагаемых, во втором – округление одного из компонентов арифметического действия, в третьем – умножение и деление на 5, 15, 25, в четвертом – применение распределительного закона. Блоки представляли собой карточки, состоящие из пяти заданий. Учащимся необходимо было не только написать ответ, но и ход решения.

Задания в карточке составлены следующим образом:

· первое задание представляло собой разобранный пример с пояснением решения;

· последующие задания были подобраны на отработку этого приема.

За каждый правильно решенный пример, мы начисляли учащимся по одному баллу, если задача вовсе не была решена, то учащийся получал 0 баллов. За все правильно решенные задания учащийся мог получить пять баллов. Таким образом, мы формировали у учащихся математические навыки по применению приемов быстрого счета.

По окончанию уроков был проведен контрольный тест в игровой форме. Каждый участник проходит пять барьеров, на которых каждому участнику разложены по одной индивидуальной задаче, при решении которой школьник использует один из приемов быстрого счета. На карточках написаны имена, и участники сначала находят свой вариант, решают его, затем подходят к судье данного барьера, называют ответ. Если ответ правильный, то судья дает жетон в знак того, что задача решена верно, а если ответ неверный, то этот этап участник проходит без жетона, возвращаться к своей задаче ему не разрешается. Тому, кто первым подойдет к финишу, дается дополнительный жетон.

По итогам «Математической эстафеты» большинство участников набрало максимальное число жетонов. Школьники продемонстрировали свои умения применять приемы быстрого счета при решении математических задач.

Таким образом, мы нашли эффективные пути повышения вычислительной культуры учащихся посредством приемов быстрого счета, поставив пред собой определенные задачи и решив их, с помощью предложенных методов.

Заключение

Приемы быстрого счета позволят без увеличения числа учебных часов повысить качество обучения и уровень математических знаний учащихся. Они служат одним из средств предупреждения формализма в преподавании математических дисциплин, делают знания более действенными, гибкими и эффективными. Изучаемые понятия рассматриваются с различных сторон, что способствует выявлению их сущности.

В данной работе рассмотрены понятия математических навыков, устные упражнения, выделены требования, предъявляемые к вычислительным умениям учащихся.

Во второй части работы даны методические рекомендации по организации устных вычислений, разобраны различные приемы быстрого счета, а так же систематизированы приемы повышения вычислительной культуры для практической работы учителя.

Считаем, что поставленные цель и задачи выпускной квалификационной работы достигнуты, гипотеза подтверждена в ходе опытного преподавания.

Работа может быть полезна учителям-практикам для систематизации и применения на уроках приемов быстрого счета.

Библиографический список

1. Методика преподавания математики [Текст]: учебник для вузов / Е.С. Канин, А.Я. Блох [и др.]; под ред. Р.С. Черкасова. – М.: Просвещение, 1985. – 268 с.

2. Хэндли, Б. Считайте в уме как компьютер [Текст] / Б. Хэндли; пер. с англ. Е.А. Самсонов. – Мн.: Попурри, 2006. – 352 с.

3. Ройтман, П.Б. Повышение вычислительной культуры учащихся [Текст]: пособие для учителей / П.Б. Ройтман, С.С. Минаев, Н.С. Прокофьева [и др.]. – М.: Просвещение, 1985. – 48 с.

4. Чекмарев, Я.Ф. Методика преподавания арифметики в 5–6 классах [Текст] / Я.Ф. Чекмарев. – М.: Учпедгиз, 1962. – 410 с.

5. Крутецкий, В.А. Психология математических способностей школьников [Текст] / В.А. Крутецкий. – М.: Просвещение, 1968. – 432 с.

6. Чекмарев, Я.Ф. Методика устных вычислений [Текст] / Я.Ф. Чекмарев – М.: Просвещение, 1970. – 238 с.

7. Глебов, И.И. Упражнения по привитию вычислительных навыков учащихся 5–9 классов средней школы [Текст] / И.И. Глебов. – М.: Просвещение, 1959. – 66 с.

8. Автайкина, А.К. Некоторые формы организации устного счёта / Математика в школе, №3, 1991 г.

9. Борткевич Л.К. Повышение вычислительной культуры учащихся» / Математика в школе, №5, 1995 г.

10. М.С. Якунина. Устные упражнения в курсе алгебры / Математика в школе, №1, 1991 г.

11. Минаева, С.С. Вычисления на уроках и внеклассных занятиях по математике [Текст] / С.С. Минаев. – М.: Просвещение, 1983. – с.

12. Гельфан Е.М. Арифметические игры и упражнения [Текст] / Е.М. Гельфан. – М.: Просвещение, 1968. – 112 с.

Содержание

Введение

1. Требования к вычислительным умениям и навыкам учащихся

1.1 Понятие математических навыков

1.2 Требования к вычислительным умениям и навыкам

1.3 Устные вычисления как основа повышения вычислительной культуры школьников

2. Методика повышения вычислительной культуры школьников

2.1 Организация устных вычислений учащихся

2.2 Приемы устных вычислений, основанные на законах и свойствах арифметических действий

2.4 Систематизация приемов повышения вычислительной культуры для практической работы учителя

2.5 Содержание и анализ опытно-экспериментальной работы

Заключение

Библиографический список

Введение

Для реализации этой цели необходимо решить следующие задачи:

1) ознакомиться с проблемой изучения вычислительной культуры учащихся;

2) изучить основные особенности математических и вычислительных навыков;

3) рассмотреть различные приемы быстрого счета как способа решения изучаемой проблемы;

4) рассмотреть применение их на уроках и внеклассных занятиях по математике;

6) проверить эффективность предложенной методики в опытном преподавании.

1. Требования к вычислительным умениям
и навыкам учащихся

Понятие математических навыков

Одной из основных задач преподавания курса математики в школе является формирование у учащихся сознательных и прочных вычислительных навыков.

Вычислительные навыки – важная составляющая математических навыков. Поэтому для начала нужно рассмотреть их общее понятие. Большая часть математических навыков – это сложные навыки, формирующиеся на основе других умений и навыков. Так, навык сложения дробей с разными знаменателями основан на умении находить наименьшее общее кратное двух натуральных чисел, применять основное свойство дроби при приведении дробей к общему знаменателю, складывать дроби с одинаковыми знаменателями. В свою очередь каждые из указанных умений и навыков также имеют сложную структуру. Отсутствие какого-либо из элементарных умений и навыков служит причиной несформированности сложного навыка.

Общеизвестно, что умения и навыки быстрее усваиваются и дольше сохраняются, если их формирование происходит на сознательной основе (дидактический принцип сознательности). Тренировки без достаточного понимания изучаемого редко приводят к прочным умениям и навыкам. Поэтому формированию навыков учащихся должно предшествовать понимание ими сути изучаемого действия.

Формирование математических навыков состоит из следующих этапов:

1. Первый этап формирования навыка – овладение умением. При овладении умением в вычислениях или тождественных преобразованиях первые упражнения на применение нового приема, метода, определения должны выполняться с подробными объяснениями и записями. Так, при изучении деления рациональных чисел следует подробно разъяснять смысл нового действия, алгоритм его выполнения. Подробные разъяснения и записи помогают ученикам лучше понять смысл и последовательность выполнения изучаемого действия. Именно поэтому на этом этапе при формировании вычислительных навыков предпочтительнее использовать письменные вычисления. Но процесс формирования навыка не ограничивается овладением умением.

2. Второй этап – этап автоматизации умения. Автоматизация умения происходит путем исключения некоторых промежуточных операций, сложные ассоциации заменяются прямыми (или спрямленными) ассоциациями от данных к искомому. Так, если умение реализуется по схеме, А→В→С, где В - промежуточное действие, то навык – чаще всего по прямой схеме А→С. Поэтому следует помочь ученикам перейти от сложной схемы действий к более простой. Это означает, что после выполнения первых упражнений надо добиваться свертывания промежуточных операций, для чего полезно часть преобразований выполнять мысленно, опуская промежуточные записи. При формировании вычислительных навыков на этом этапе используют письменные вычисления с промежуточными устными.

Актуальным является методическое требование выполнять устно вычисления и преобразования не только во время так называемых пятиминуток устного счета. При решении любых задач, на каждом этапе урока все вычисления и выкладки, которые ученики могут выполнять устно, должны быть устно и выполнены. И дело не только в том, что на лишние записи тратится драгоценное время урока. Гораздо хуже то, что учащихся с самого начала приучают не думать при вычислениях, а только применять стандартный алгоритм, что в дальнейшем приводит ко многим нерациональным решениям, к новым большим потерям учебного времени, к слабо развитым вычислительным умениям и навыкам. Привычка выполнять устно несложные вычисления и выкладки нередко порождает потребность производить мысленные эксперименты при решении задач, высказывать догадки, предположения о путях решения более сложных задач, мысленно (устно) проверяя истинность предположений. А это одно из главных условий обучения решению математических задач. Кроме того, по мере овладения навыками целесообразно не только опускать промежуточные записи, стремиться выполнять часть вычислений и преобразований устно, но и переписывать выражения после преобразований не одного, а 2–3 отдельных выражений, входящих в состав сложного выражения, что также сокращает записи и время решения задач.

Несколько слов нужно сказать и о проблеме рациональности в вычислениях. В требование рационального выполнения вычислений и преобразований включается как выбор и осуществление рационального пути выполнения упражнений и решения задач, так и их рациональная запись.

Выбору рационального пути решения всегда предшествует анализ данного для вычисления или преобразования выражения, выявление порядка заданных операций, мысленный эксперимент («Если поступить так, то получится то-то, а если иначе-то… Какой путь проще?»). На этой основе составляется план вычислений, преобразований. Обдуманное составление плана существенно помогает выбору рационального пути решения. Рациональное же решение – способ развития мышления учащихся, формирования высокоразвитых, осмысленных умений и навыков, свидетельствующий о бережном отношении учителя к учебному времени учащихся. Рассмотрение различных вариантов преобразования одного и того же выражения и выбор наиболее рационального – один из путей обучения рациональным решениям.

Рациональное выполнение вычислений и тождественных преобразований требует нестандартных решений, следовательно, служит формированию более прочных умений и навыков. Задача учителя систематически обращать внимание школьников на рационализацию вычислений и преобразований.

Форма записи решения задач может иметь немалое значение в формировании навыков. Не следует рекомендовать единую форму записи решения на всех этапах обучения, в процессе отработки умений и навыков форма записи вычислений и тождественных преобразований должна, как правило, упрощаться.

Таким образом, подчеркнув особенности математических навыков, можно переходить к рассмотрению частного случая – вычислительным навыкам.

Требования к вычислительным умениям и навыкам

· отчетливо писать математические символы (цифры, знаки препинания, знаки арифметических действий);

· цифры и знаки располагать строго в соответствии с правилами арифметических действий;

· безошибочно применять таблицы сложения и умножения натуральных чисел.

Для того чтобы овладеть умениями, предусмотренными программой, учащемуся достаточно уметь устно:

· складывать и умножать однозначные числа;

· прибавлять к двузначному числу однозначное;

· вычитать из однозначного или двузначного числа однозначное (преимущественно из числа, меньшего 20);

· складывать несколько однозначных чисел;

· складывать и вычитать двузначные числа;

· делить однозначное или двузначное число на однозначное нацело или с остатком;

· производить действия (на основе знаний правил) с дробными числами.

1. Ознакомить учащихся с принципом работы того или иного нового для них вычислительного алгоритма.

Дата: 2019-07-24, просмотров: 197.

12 3 4 5 6 7 8 9 10 Следующая ⇒