В данной работе рассматривается радиолокационная установка, которая представляет собой совокупность как минимум двух синхронно вращающихся антенн. В данной системе одна из антенн является ведущей — она задает параметры движения, другая — ведомая, которая должна в точности повторять траекторию движения ведущей.

Каждая из антенн представляет собой сложную электромеханическую систему, представляющую собой совокупность таких составных частей как электропривод, редуктор и собственно принимающая антенна. Основным источником механической энергии является электропривод. Редуктор служит для преобразования угловых скоростей и соответственно вращающих моментов, выдаваемых двигателем. Редукторы могут быть зубчатые (в том числе червячные) или гидравлические.

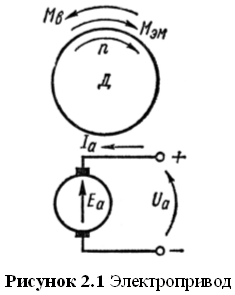
Напомним, что в разделе 1.5 были сделаны следующие допущения: в данной системе есть возможность измерять в каждые заданные моменты времени положение ведущей антенны, т.е. есть возможность получать информацию о траектории ведущей антенны; тип двигателя, приводящего в движение антенны является не существенным для данной работы.

Применяемые в настоящее время регулируемые и следящие электроприводы (ЭП) построены, в основном, с применением принципов подчиненного регулирования координат. В качестве координат выступают ток якоря двигателя, его скорость вращения и угол поворота вала двигателя (перемещение исполнительного органа рабочей машины).

Для решения поставленных в разделе 1.5 задач нет необходимости приводить полное точное математическое описание данной электромеханической системы. Так как нашей целью является не описание процессов, протекающих внутри этой системы, а регулирование поведения данной системы в целом. К тому же, как было видно из описанного выше, современные электромеханические системы имеют сложную структуру и их описание будет громоздким, что не дает возможности применения этого описания в однокристальных ЭВМ, на которые ориентируется данный разрабатываемый метод.

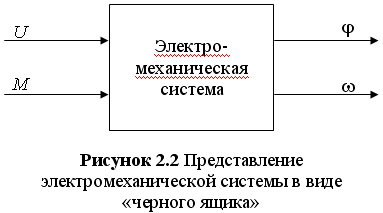
В связи с этим предлагается рассматривать данную электромеханическую систему как один неразделимый блок, не останавливаясь на конкретных процессах и взаимосвязях имеющих место быть, т.е. рассматривать данную систему как, так называемый, «черный ящик». На рисунке 2.2 приведена условное изображение этой системы в виде «черного ящика». Известно, что выходными координатами системы являются угол j и скорость w поворота исполнительного органа рабочей машины (вала двигателя). Входной координатой является момент М, характеризующий тормозящий момент на валу двигателя, развиваемый рабочей установкой; момент сил трения в подшипниках, о воздух, на коллекторе электрической машины и в зубчатых передачах редуктора; тормозящий момент, вызываемый потерями на гистерезис и вихревые токи в сердечнике якоря. Управляющим параметром, в данном случае, является напряжение U на якоре электродвигателя.

Объекты и системы управления состоят из элементов, имеющих различную природу. Для анализа их взаимодействия удобно перейти к единообразному, стандартному описанию.

Так как разрабатываемый метод ориентируется на использование в однокристальных ЭВМ, то описание системы необходимо производить в дискретном виде. Для этого в описании динамической системы вместо дифференциальных уравнений предложено использовать уравнения в конечных разностях или разностные уравнения.

Для математического описания данной системы было предложено использовать разностное уравнение специального вида, которое носит название авторегрессионно-регрессионной модели объекта (АРРМ).

Общий вид авторегрессионно-регрессионной модели порядка ( N, L) представлен ниже:

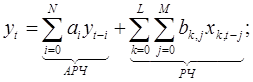                                                  (2.1)

где АРЧ — авторегрессионная часть, РЧ — регрессионная часть; N и L — целые числа, определяющие порядок АРРМ ( 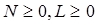); N — порядок авторегрессионной, а L — порядок регрессионной части модели; a_i и b_i — параметры АРРМ. Вектор параметров определяется на этапе идентификации модели.

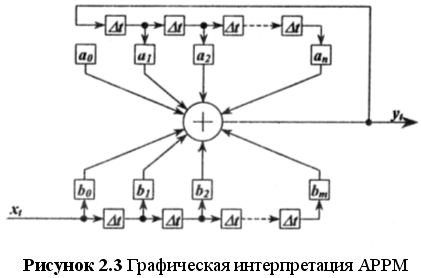
Авторегрессионная часть является выходом модели, а регрессионная часть — входом, т.е. y_t является выходным процессом, а x_t — входным. В частном случае, когда N = 0, модель не имеет входа и называется авторегрессионной моделью, если L = 0, то будет получена регрессионная модель. Графическая интерпретация АРРМ приведена на рисунке 2.3. В отличие от дифференциальных уравнений, авторегрессионно-регрессионные модели могут описывать как непрерывные, так и дискретные по своей природе объекты.

В нашем случае входными процессами являются момент М и напряжение на якоре двигателя U, которое также является управляющим воздействием. Выходным параметром является угол поворота оси антенны. Таким образом вид авторегрессионно-регрессионной модели в нашем случае будет иметь вид:

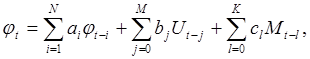                                      (2.2)

или если принять в качестве выходного параметра скорость w поворота вала, то выражение (2.2) примет вид:

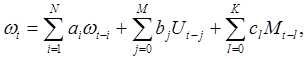                                       (2.3)

где 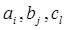 — параметры модели, (N, M+ K) — порядок модели.

В режиме холостого хода выражения (2.2) и (2.3) будут иметь вид:

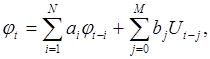                                                          (2.4)

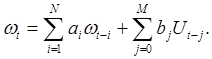                                                          (2.5)

Параметры этих моделей не имеют прямого физического смысла и зависят от выбора шага квантования по времени. Порядок модели как и ее параметры находятся в процессе идентификации.

По своему физическому смыслу модели (2.3) и (2.5) являются устойчивыми, а (2.2) и (2.4) — неустойчивыми. Модели (2.2) и (2.4) являются неустойчивыми, так как выходная координата (угол поворота) постоянно увеличивается при постоянном входном воздействии (напряжении на якоре), а скорость вращения стремится к некоторому определенному значению.

Авторегрессионно-регрессионная модель является устойчивой, если устойчивой является соответствующая ей авторегрессионная модель. Выполнить анализ устойчивости можно после идентификации параметров модели.