Цель:
· выработать умение решать неравенства второй степени с одним неизвестным и системы квадратных неравенств.
Решение квадратных неравенств – это традиционно обособленная часть исследования свойств квадратичной функции. Например, задача о решении неравенства х2-5х+6<0 может быть переформулирована в задачу о нахождении промежутков, на которых функция у =х2-5х+6 принимает отрицательные значения, а это легко решается с помощью эскиза графика. Этот способ фактически является строгим обоснованием графического способа.
Метод интервалов является логическим продолжением решения квадратных неравенств. Он позволяет решать более сложные неравенства, у которых левая часть – многочлен любой степень, представляемый в виде простых множителей, или дробь, у которой числитель и знаменатель также многочлены, разлагаемые на множители.
В результате изучения темы учащиеся должны уметь:
· решать квадратные неравенства с одной неизвестной графически и методом интервалов
Специфические действия:
1. Привидение неравенства к квадратному виду.
2. Решение квадратных уравнений.
3. Построение графиков функций (схематично).
4. Выполнение тождественных преобразований.
5. Определение знака выражения на соответствующих промежутках.
6. Алгоритм решения квадратных неравенств с одной переменной.
«Ядерным» материалом темы является:
1. Понятия «< » , « > » неравенство, решение неравенства решение системы неравенств, равносильных неравенств;
2. Свойства числовых неравенств, равносильных неравенств;
3. Алгоритм решения квадратных неравенств с одной переменной и решения системы неравенств.
4. Свойства графика квадратичной функции.
Рассмотрим работу с алгоритмом решения неравенств второй степени (графически) поэтапно. На первом этапе полезно актуализировать знания: нахождение корней квадратного трёхчлена, дискриминанта, изображение графиков квадратичных функций (схематично). После этого формулируем сам алгоритм. На втором этапе отрабатываем отдельные операции, входящие в алгоритм: изображение графиков функций, нахождение при каких значениях х функция принимает положительные, а при каких отрицательные значения. На третьем этапе применяем алгоритм при решении более сложных задач.
I. Введение алгоритма.
Рассмотрим введение алгоритма “решение неравенств второй степени с одним неизвестным” (графическим методом) с использованием обучающих самостоятельных работ.
1.Актуализация знаний
Обучающую самостоятельную работу проводим по новому материалу,
| |
| |
 но перед этим повторим ранее изученные понятия, которыми придётся воспользоваться.
но перед этим повторим ранее изученные понятия, которыми придётся воспользоваться.
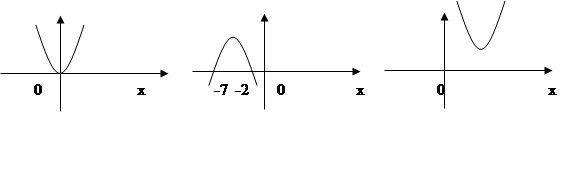 1. у у у
1. у у у
| |
а) Куда направлены ветви параболы?
b) Пересекает ли парабола ось ох, если да то сколько раз?
с) При каких х парабола принимает положительные значения?
d) При каких х парабола принимает отрицательные значения?
2. Изобразите схематично график функции.
· у=х2+5х-6
· у=-х2+4х-4
· у=3х2+4х+8
· у=0,1х2+3х-6
3. Изобразите схематично параболу, которая на
· промежутке (-∞;-3] убывает, а на промежутке [-3;+ ∞) возрастает;
· промежутке (-∞;6] возрастает, а на промежутке [6;+ ∞) убывает;
4. При каких значениях х , функция принимает положительные значения
· f(x)=-x2+4x-2;
· f(x)=3х2+2х-1;
5. При каких значениях х , функция принимает отрицательные значения
· f(x)=-х2+4х-1;
· f(x)=4x2+2x-1;
2. Открытие алгоритма учащимися под руководством учителя .
После этого начинается работа с объяснительным текстом. Каждый ученик самостоятельно изучает этот текст. Это предполагает активную работу мысли ученика. Текст составлен таким образом, чтобы учащиеся в меру возможностей самостоятельно выводили формулы, находили нужные приёмы решения задачи.
Если в левой части неравенства стоит квадратный трёхчлен, а в правой – нуль, то такое неравенство называют квадратным. Например, неравенства
2х2-3х+1≥0, -3х2+4х+5<0 являются квадратными.
Решением неравенства с одним неизвестным называется то значение неизвестного, при котором это неравенство обращается в верное числовое неравенство.
Решить неравенство – найти все его решения или установить, что их нет.
Решение неравенства второй степени с одной переменной можно рассматривать как нахождение промежутков, на которых соответствующая квадратичная функция принимает положительные и отрицательные значения.
Например, решим с помощью свойств графика квадратичной функции неравенство 2х2-х-1≤0
График квадратичной функции у=2х2-х-1 – парабола, ветви которой направлены вверх.
Найдём точки пересечения этой параболы с осью ох, для этого решим квадратное уравнение 2х2-х-1=0. Корни уравнения х1=1, х2=-0.5
Следовательно парабола пересекает ось ох в точках х1=1, х2=-0.5
Покажем схематично как расположена парабола в координатной плоскости.

|
Из рисунка видно, что неравенству 2х2-х-1≤0 удовлетворяют те значения х, при которых значения функций равны нулю или отрицательны то есть те значения х при которых точки параболы лежат на оси ох или ниже этой оси. Из рисунка видно, что этими значениями являются все числа из отрезка
[-0.5;1].
Ответ: -0.5≤х≤1
График этой функции можно использовать и при решении других неравенств, которые отличаются от данного только знакомом неравенства, из рисунка видно, что:
1) решениями неравенства 2х2-х-1 < 0 являются числа интервала -0.5<х<1
2) решениями неравенства 2х2-х-1 > 0 являются все числа промежутков
х<-0.5 и х>1.
3) решениями неравенства 2х2-х-1 ≥ 0 являются все числа промежутков
х ≤-0.5 и х ≥ 1.
После работы с объяснительным текстом учащиеся получают «нулевые» задания. Они предназначены для самоконтроля и к ним предлагаются правильные ответы. Если ответы учеников не совпали с данными ответами, то придётся повторно прочитать объяснительный текст и снова выполнить «нулевые» задания, устранив ошибки.
10 Решите неравенства:
а) 4х2-5х+6х<0,2(10х2+15)
1. Приведите неравенство к квадратному виду .
2 Выясните имеет ли выражение, стоящее в левой части корни.
(Решите уравнение, приравняв выражение в левой части к нулю.)
Заполните таблицу
| Д>0 | Д<0 | Д=0 | |||
| Количество корней | |||||
| Найдите и отметьте корни на числовой оси (корни разбивают числовую ось на промежутки) |
| ||||
| Изобразите схематично параболу | |||||
| Выберите промежутки, в которых выражение имеет требуемый знак, и запишите ответ. |
Аналогично решите неравенства
b) х2+2х+1≥0 (Заполните таблицу)
c) -х2+х-1≥0 (Заполните таблицу)
Формулировка алгоритма.
20. Сформулируйте этапы решения квадратных неравенств (графическим методом).
Ответы:
1. а)1<х<1.5
b) х – любое число;
c) нет решения.
2. Алгоритм решения квадратных неравенств с одной переменной (графическим методом)
1.Перенесите все слагаемые в левую часть и решите уравнения, приравняв выражение в левой части к нулю (найдите дискриминант квадратного трёхчлена, и выясните, имеет ли трёхчлен корни).
2. Если трёхчлен имеет корни, то отметьте их на оси абсцисс и через отмеченные точки проведите схематично параболу ветви которой направлены вверх при а>0 или вниз при а<0, если трёхчлен не имеет корней, то схематично изобразите параболу, которая расположена в верхней полуплоскости при а>0 или в нижней полуплоскости при а<0.
3. Найдите на оси ОХ промежутки, для которых точки параболы расположены выше оси ох (если ах2+вх+с>0) или ниже оси ох (если ах2+вх+с<0).
4.Запишите ответ, взяв эти промежутки в объединение.
II Усвоение.
Составной частью работы с алгоритмом является система упражнений, предназначенных для осознания учащимися изучаемого материала, более глубокого его усвоения, формирования необходимых понятий. По ходу выполнения упражнений в задачах даются дополнительные разъяснения, а к наиболее трудным – ответы.
1. Приведите неравенства к квадратному виду
1) у2+5у2-3у>5(у+1)
2) 0.2(z+4)-0.8≥1.2z+2
3) 6+m2+m<m(2m2-6)
2.(устно) Используя график функции у=ах2+вх+с (см рис). указать, при каких значениях х эта функция принимает положительные значения; отрицательные значения; значения равные нулю.

у у у

-3
3. Построить график функции f(x) (схематично). Определить по графику значения х при которых функция принимает положительные значения, отрицательные значения.
1) 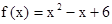
2) 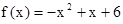
3) 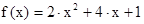
4.Решите графически неравенства
1) 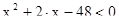
2) 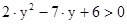
3) 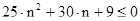
4) 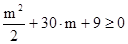
4. Найдите, при каких значениях х трёхчлен
· 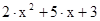 принимает положительные значения;
принимает положительные значения;
· 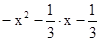 принимает отрицательные значения;
принимает отрицательные значения;
5. Решите неравенства.
a) х2<16;
b) х2≥3;
c) 0,2х2 >1,8;
d) -5х2≤х.
6.Найдите множество решений неравенств:
a) 3х2+40х+10<-х2+11х+3;
b) 9х2-х+9≥3х2+18х-6;
c)2х2+8х-111<(3х-5)(2х+6).
7. Докажите, что при любом значении переменной верно неравенство:
a) 4х2+12х+9≥0;
b) -5х2+8х-5<0.
III.Применение алгоритма
На этом этапе работы с алгоритмом задания предлагаются аналогичные рассмотренным, но с постепенным усложнением. В ходе решения учитель проверяет правильность понимания учащимися изученного вопроса, уточняет формулировки, разъясняет допущенные ошибки.
1.Решите неравенство.
1) 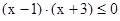
2) 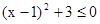
3) 2x (3x-1)>4x2+5x+9
4) (5x+7)(x-2)<21x2 -11x-13
2. Найдите общее решение неравенств х2+6х-7 ≤ 0 и х2-2х-15 ≤ 0
3.Докажите, что:
· х2+7х+1>-x2+10x-1 при любом х;
· -2х2+10х<18-2x при х≠3.
4. Одна сторона прямоугольника на 7 см больше другой. Какой может быть сторона, если площадь прямоугольника меньше 60 см2.

 5. Найдите область определения функции.
5. Найдите область определения функции.
· 
 у = 12х-3х2
у = 12х-3х2
· у = 1/ 2х 2 -12х+18
После того как учащиеся познакомились с графическим методом, предлагается метод интервалов – как ещё один из способов решения квадратных неравенств.
Формирование алгоритма решения квадратных неравенств с одним неизвестным (методом интервалов) можно осуществить аналогичным образом.
Алгоритм решения неравенства второй степени c одним неизвестным (методом интервалов).
1. Раскройте скобки в обеих частях неравенства (если есть дробные коэффициенты, то неравенство освободить от дробей).
2. Перенесите все слагаемые в левую часть, приведите подобные члены (если нужно).
3. Решите уравнения, приравняв выражение в левой части к 0 (найдите дискриминант и выясните, имеет ли трёхчлен корни).
4.Найденные корни уравнения нанесите на числовую ось. Эти корни разбивают числовую ось на промежутки, на каждом, из которых выражение, стоящее в левой части, сохраняет знак.
5. Выберите на каждом из промежутков какое – нибудь значение (пробную точку) и определите знак выражения в этой точке.
6. Выберите промежутки, в которых выражение имеет требуемый знак, и запишите ответ, взяв их в объединение.
1. Актуализация знаний
1. ах2+вх+с=0
1) Решите квадратное уравнение.
2) Разложите левую часть уравнения по формуле ах2+вх+с=а(х-х1)(х-х2), где х1,х2 – корни данного уравнения.
2.Найдите корни уравнения, разложите уравнение по корням, отметьте корни на числовой оси.
· 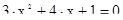
· 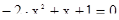
3.Разложите многочлен на множители
· 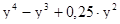
·
| |
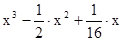
II Усвоение
1. Сведите следующие неравенства к квадратному.
1) 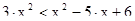
2) 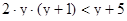
3) 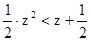
2. Найдите при каких значениях х трёхчлен
· 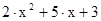 принимает положительные значения;
принимает положительные значения;
· 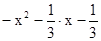 принимает отрицательное значения;
принимает отрицательное значения;
3. Решите неравенства
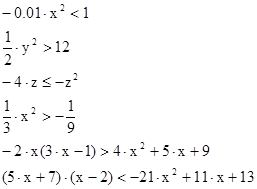
4. Длина прямоугольника на 5 см. больше ширины. Какую ширину должен иметь прямоугольник, чтобы его площадь была больше 36см2.
5. При каких значениях х функция у= - х2 + 8х + 2 принимает значения больше 9.
6. Разложите многочлен на множители.
· 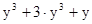
· 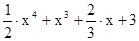
· 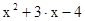
7. Решите неравенство методом интервалов.
· 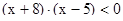
· 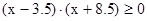
· 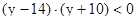
· 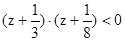
· 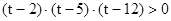
· 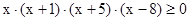
8. Найдите область определения выражения.
1) 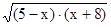
2) 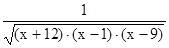
9. Решите неравенство
1) 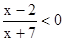
2) 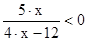
3) 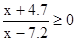
III.Применение алгоритма
1. Решите неравенство.
1) 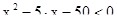
2) 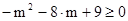
3) 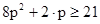
4) 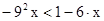
2. Найдите общее решение х2+6х-7 ≤ 0 и х2-2х-15 ≤ 0
3.Решите систему неравенств.
1) 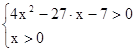
2) 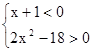
3) 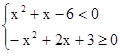
4.Катер должен не более чем за 4 часа пройти по течению реки 22,5км и вернуться обратно. С какой скоростью относительно воды должен идти катер, если скорость течения равна 3км/ч.
5.Решите неравенство методом интервалов.
1) 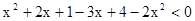
2) 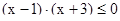
3) 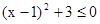
6.Решите неравенство.
1) 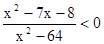
2) 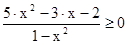
3) 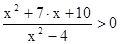
Опытное преподавание.
Факультативное занятие в девятом классе (решение неравенств с параметром первой степени с одной неизвестной).
Цель:
применить алгоритмический метод при формировании умений и навыков в решении линейных неравенствах с параметрами.
Задачи:
· расширить кругозор учащихся;
· воспитание внимания, аккуратности, самостоятельности;
· осуществление взаимосвязи теории и практики;
· развитие памяти, логического мышления.
Решение задач с параметрами всегда вызывает большие трудности у учащихся. Причём часто учащиеся испытывают психологические трудности, «боятся» таких задач, так как не видят связи в их решении с решениями линейных неравенств с одной переменной.
Изучение линейных неравенств с параметром первой степени с одной неизвестной не возможно без умения решать линейные неравенства с одной переменной. Так как факультатив проводился в 9 классе, а линейные неравенства изучались в восьмом классе, то возникла необходимость актуализировать знания по решению линейных неравенств, вспомнить этапы их решения. Ученикам можно предложить следующее задание.
Решите неравенство 2(х+5)-3≥4+3х
Все решают у себя в тетрадях, а один ученик решает у доски. Запись ведёт в два столбика. Решение в одном столбика, а в другом записывают пояснения к своим действиям.
 2х+7≥4+3х Раскрыли скобки в обеих частях неравенства
2х+7≥4+3х Раскрыли скобки в обеих частях неравенства
2х-3х≥4-2 Перенесли слагаемые, содержащие переменную в одну
часть, а не содержащую в другую.
-х≥2 Привели подобные члены в каждой части.
х≤-2 Разделили обе части неравенства на коэффициент при
 переменной (учитывая его знак !).
переменной (учитывая его знак !).
 Отметили соответствующие промежутки на
Отметили соответствующие промежутки на
координатной прямой.
х 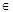 (-∞;-2] Записали числовой промежуток
(-∞;-2] Записали числовой промежуток
После того как повторили этапы решения линейных неравенств с одной переменной, учитель предлагает на доске подробный разбор решения неравенства с параметром. Затем ученики вместе с учителем формулируют алгоритм решения линейных неравенств с параметром.
Пример 1. Рассмотрим решение неравенства (а-4)∙х<12
Чтобы найти х, обе части неравенства хочется разделить на (а-4). Однако теперь важно положительно, отрицательно или равно нулю выражение (а-4).
Определим знак выражения
|
|



|


Рассмотрим три случая:
a) а-4=0
b) а-4>0
c) а-4<0
1)если а-4=0 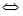 а=4, то неравенство примет вид 0х<12, которое справедливо для всех х
а=4, то неравенство примет вид 0х<12, которое справедливо для всех х 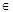 R
R
2) a-4>0 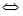 a>4, то разделим обе части неравенства на положительное выражение (а-4), не меняя знак неравенства, получим х >
a>4, то разделим обе части неравенства на положительное выражение (а-4), не меняя знак неравенства, получим х > 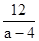 (используем свойство числового неравенства).
(используем свойство числового неравенства).
3) a-4<0 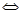 a<4, то разделив обе части неравенства на отрицательное выражение и поменяв знак неравенства, получим х<
a<4, то разделив обе части неравенства на отрицательное выражение и поменяв знак неравенства, получим х< 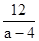 .
.
Ответ:
если а=4, то х 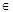 R;
R;
если а>4, то х > 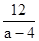 ;
;
если а<4, то х< 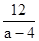 .
.
Таким образом, после разобранного примера учитель формулирует алгоритм, опираясь на знания и умения, учащихся о решении линейных неравенств с одной переменной.
1. Раскрыть скобки в обеих частях неравенства (если есть дробные коэффициенты, то неравенство освободить от дробей).
2. Перенести слагаемые, содержащие переменную в одну часть, а не содержащие в другую.
3. Привести подобные члены в каждой части и получить один из 4 видов неравенств А(а)х<B(a) (**) , А(а)х≤B(a), А(а)х>B(a), А(а)х≥B(a), где х- переменная, А(а) и В(а) – функции параметра а.
4. Рассмотреть три случая:
1) Найти а, при которых А(а)=0, подставить в неравенство(**) вместо параметра а найденные решения и решить соответствующие неравенства.
2) Найти а, при которых А(а)>0, разделить неравенство(**) на А(а), не меняя его знак.
3) Найти а, при которых А(а)<0, разделить неравенство(**) на А(а), поменяв его знак.
5. Записать ответ.
Пример 2. решить неравенство



|

 3-а∙х ≥ х
3-а∙х ≥ х  х+а∙х≤3
х+а∙х≤3 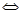 х∙(1+а)≤3
х∙(1+а)≤3
1) 1+а=0 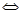 а=-1
а=-1
Подставляем в неравенство 0∙х≤3, х 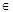 R.
R.
2) 1+а>0 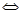 а>-1
а>-1
х≤ 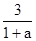
3) 1+а<0 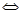 а<-1
а<-1
x≥ 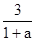
Ответ: При а=-1, то х 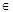 R;
R;
а>-1, то х ≤ 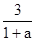 ;
;
а<-1, то x ≥ 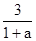 .
.
Пример 3.
х∙а2 ≤ а+х  х∙ (а2-1) ≤ а
х∙ (а2-1) ≤ а




 1) а2-1=0
1) а2-1=0  (а-1)(а+1)=0
(а-1)(а+1)=0  а=1 или а=-1
а=1 или а=-1
|
|
 а = 1; а = -1; х∙0 ≤ 1 неверно
а = 1; а = -1; х∙0 ≤ 1 неверно
2) а2-1>0  а>1 или a<1, то x ≤
а>1 или a<1, то x ≤ 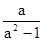
3) а2-1>0  a
a 
 , то x
, то x 
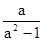
Ответ: а=1, то х 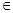 R;
R;
а= -1, то нет решения;
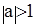 , то x ≤
, то x ≤ 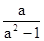 ;
;
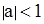 , то x
, то x 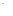
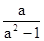 .
.
Пример 4.
2а∙(а-2) ∙х 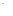 а-2
а-2
1) 2а∙(а-2)=0  а=0 или а=2
а=0 или а=2
а=0 х∙0  -2 верно
-2 верно




 а=2 х∙0
а=2 х∙0  0 неверно
0 неверно
2) 2а∙(а-2)>0 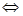 а
а 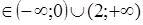 ,
,
то х 
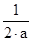
3) 2а∙(а-2)<0 
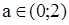 , то х
, то х 
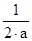
Ответ:
а=0, то х 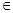 R;
R;
а=2, то нет решения;
а 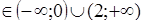 , то х
, то х 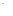
 ;
;
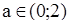 , то х
, то х 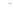
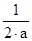 .
.
Пример 5.
(а2-9) ∙х 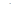 а+3
а+3



 1) а2-9=0
1) а2-9=0
а=3 и а=-3
а=3 0х 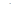 6 верно;
6 верно;
а=-3 0х 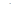 0 верно;
0 верно;
2) 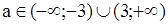
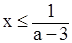 ;
;
3) 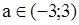
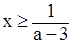 ;
;
Ответ:
а=3 , а=-3 то х 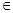 R;
R;
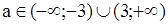 , то
, то 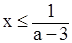 ;
;
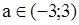 , то
, то 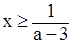 ;
;
Пример 6.
а2х-а ∙х > a-1  x∙ (a2-a) > a-1
x∙ (a2-a) > a-1 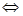 x∙(a∙ [a-1]) > a-1
x∙(a∙ [a-1]) > a-1
1) a∙ [a-1]=0 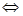 a=0 и а=1
a=0 и а=1


 а=0 0∙х>-1 верно
а=0 0∙х>-1 верно
а=1 0∙х>0 неверно
2) 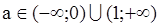 ; х>
; х> 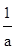
3)а 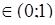 ; х<
; х< 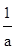
Ответ:
а=0, то х 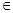 R;
R;
а=1, то нет решения;
a 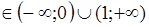 , то х>
, то х> 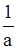 ;
;
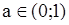 , то х<
, то х< 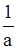 .
.
Пример 7.
а2∙х+4а∙х-а-4≤0
Ответ:
а=0 , а=-4 то х 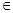 R;
R;
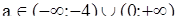 , то
, то 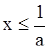 ;
;
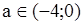 , то
, то 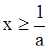 .
.
Пример 8.
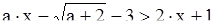
Ответ:
a<-2 а=2, то нет решения;
а 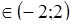 , то х <
, то х < 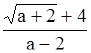 ;
;
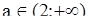 , то х>
, то х> 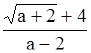 .
.
Примеры для самостоятельного решения:
1)2∙а∙х+5>а+10∙x;
2)a∙x+x+1 <0;
3)x+1≤a∙x+a2;
4)a∙x+16≤a2-4∙x;
5)m∙x>1+3∙x;
6) 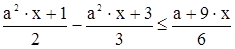 ;
;
7) 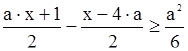 ;
;
8) (x-1) ∙ (a2-1)>5-4∙a;
9)b-3∙b+4∙b∙x<4∙b+12∙x;
Выводы:
Факультатив “Решение неравенств с параметром первой степени с одной неизвестной” был проведён в 9 классе в школе №52 г. Кирова. Цель данного факультатива была достигнута. Применение алгоритмического метода позволило сделать изложение данной темы более доступным, учащиеся научились решать линейные неравенства с параметром осознанно.
Заключение
В ходе исследования были решены следующие задачи:
1) Изучена учебно-методическая литература по применению алгоритмического метода в школе;
2) Рассмотрены следующие вопросы, связанные с алгоритмическим методом: история возникновения алгоритма; определение алгоритма, его свойства, основные этапы алгоритмического процесса и классификация алгоритмов.
3) Разработана методика формирования алгоритмов “Решение алгебраических неравенств 1 и 2 степени с одним неизвестным”.
4) Показано как алгоритмический метод может применяться при решении линейных неравенств с параметром на факультативном занятии.
Литература
1. Алгебра: Учеб. Для 7 кл. / Алимов Ш.А., Ю.М. Колягин, Ю.В. Сидоров и др – М: Просвещение, 1999.
2. Алгебра: Учеб. Для 7 кл. общеобразовательных учреждений / Под редакцией С.А. Теляковского – М: Просвещение, 2002.
3. Алгебра: Учеб. Для 8 кл. / Алимов Ш.А. ., Ю.М. Колягин, Ю.В.Сидоров и др – М: Просвещение, 1991.
4. Алгебра: Учеб. Для 8 кл. общеобразовательных учреждений / Под редакцией С.А. Теляковского – М: Просвещение, 1996.
5. Алгебра: Учеб. Для 9 кл. / Алимов Ш.А. ., Ю.М. Колягин, Ю.В.Сидоров и др – М: Просвещение, 1992.
6. 4. Алгебра.8 класс./Под ред. Виленкина Н.Я.- М: Просвещение, 1997.
7. 5.Алгебра.9 класс./Под ред. Теляковского С.А.- М: Просвещение, 1994.
8. 6.Алгебра в 8 кл: Методическое пособие для учителей – М: Просвещение, 1977.
9. 7.Алгебра в 9 кл: Методическое пособие для учителей – М: Просвещение, 1978.
10. Бочарова О. Урок применения свойств линейных неравенств с одной переменной. // Математика в школе – 2002 - №7 – с. 40 – 42.
11. Виленкин Н.Я., Жохов В.И., Чесноков А.И. Математика: Учебник для 5 класса.- М: Мнемозина, 1999.
12. Галицкий М.Л., Гольдман А.Н., Завич Л.И. Курс алгебры 8-го класса в задачах- Львов: Журнал «Квантор», 1991.
13. Горбачёв В.И. Общие методы решения уравнения и неравенства с параметрами не выше 2 степени. // Математика в школе – 2000 - №2 – с. 61-68.
14. Башмаков М.И. Уравнения и неравенства – М: Наука, 1971.
15. Богушевский К.С., Сикорский К.Л. Сборник задач по математике для повторения.: Пособие для учителей 5-8 классов средней школы –М: Учпедгиз, 1955.
16. Варпаховский К.М. Элементы теории алгоритмов.- М., 1997.
17. Горнштейн П.И., Полонский В.Б., Якир М.С. Задачи с параметрами. – Киев
18. Ефремов Д.Н. Алгоритмы.- С.-Петербург, 1993.
19. Задачи по математике: Уравнения и неравенства: Справочное пособие. /Вавилов В.В. –М: Наука, 1988.
20. Здоровенко М.Ю.
21. Косовский М.А. Основы теории элементарных алгоритмов. - М.: 1987.
22. Королева Т. Математический тренажёр по алгебре для 7- 9 классов. // Математика в школе – 2001 - №8 – с.12-30.
23. Коровкин П.П. Неравенства М: Гос. изд-во технтко-теоретич. лит., 1951.
24. Кузнецова Л. Методические указания к теме “Неравенства ” // Математика в школе – 2002 - №6 – с.22-32.
25. Кривоногов В. Квадратные неравенства и уравнения. //Математика – 2002 - №3 (16-22 января) – с.15-19.
26. Лабораторные и практические работы по методике преподавания математики. /Под ред. Лященко Е.И. - М: Просвещение,1988.
27. Ланда Л.Н. Алгоритмизация в обучении.- М.: Просвещение, 1966.
28. Математика. Арифметика. Алгебра. Анализ данных 8 кл: учебник для общеобразовательных учебных заведений. / Под редакцией Г.В. Дорофеева – М: Дрофа, 1998.
29. Математика. Арифметика. Алгебра. Анализ данных 9 кл: Учебник для общеобразовательных учебных заведений. / Под редакцией Г.В. Дорофеева – М: Дрофа, 1998.
30. Математика: Учебник для 5 класса/ Под ред. Дорофеева Г.В., Шарыгина И.Ф. - М.: Просвещение, 1994.
31. Методика преподавания математики в средней школе. /Под ред. Мишина В.И. – М.: Просвещение 1987. Талочкин П.Б. Неравенства и уравнения. – М.: Просвещение, 1970.
32. Мордкович А.Г. Алгебра 8 кл. : Задачник для общеобразовательных учреждений. – М.: Мнемозина , 2001.
33. Мордкович А.Г. и др. Алгебра 8 кл: Учебник для общеобразовательных учреждений – М: Мнемозина, 2002.
34. Мордкович А.Г. и др. Алгебра 9 кл: Задачник для общеобразовательных учреждений – М: Мнемозина, 2000.
35. Мордкович А.Г. и др. Алгебра 9 кл: Учебник для общеобразовательных учреждений – М: Мнемозина, 2000.
36.Мордкович А.Г. Алгебра: Методическое пособие для учителей.- М: Мнемозина, 1997.
37. Невяжский Г.Л. Неравенства. : Методическое пособие для учителей. – М., 1997.
38. Психология. / Под ред. Ковалёва Л.И., Степанова М.П., Шабалина Г.Т.,
Талочкин П.Б. Неравенства и уравнения. – М.: Просвещение, 1970
39. Симонов А. Дидактические материалы для 8-9 классов с углублённым изучением математики. // Математика в школе – 2002 - №7 – с.5-10.
40. Факультативный курс по математике: Учебное пособие для 7-9 классов средней щколы /сост. Никольская И.Л. – М.: Просвещение, 1991.
Дата: 2019-07-24, просмотров: 458.