Метод Рунге-Кутта 4-ого порядка обладает в отличие от метода трапеций не 2, а 4 промежуточными вычислениями приращений.

Итерационная формула метода выглядит так:

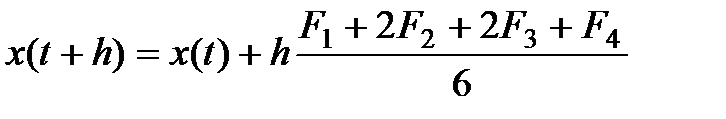,                        (2.31)

где ;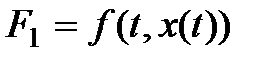

;

.

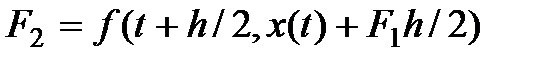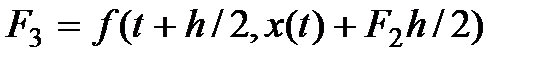
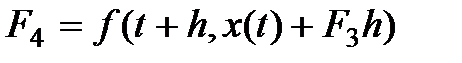Метод Рунге-Кутта 4-ого порядка обладает ошибкой четвертого порядка - .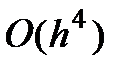

Решатели моделирующих программ

Под решателями моделирующих программ понимают набор процедур (методов) позволяющих проводить моделирование систем различных классов.

В системах моделирования выделяют:

1) Итерационный решатель - предназначен для численного решения систем алгебраических уравнений 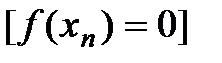(нахождение таких значений независимых переменных 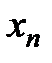, которые обнулят систему полиномов 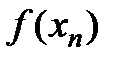). Используются методы Ньютона, Ньютона-Рафсона и т.д.

2) Решатель ДУ – предназначен для численного решения систем ДУ. Широко известны и находят применение два алгоритма программ численного интегрирования используемых в решателях ДУ: одношаговый многостадийный (все перечисленные выше методы) и многошаговый.

Реализация многостадийных методов интегрирования (больше 1-ой стадии) требует наличия в системе итерационного решателя. При его отсутствии данные методы невозможно применять в системах с обратными связями.

Так как в разрабатываемой системе моделирования итерационный решатель не был реализован, то решатель ДУ использует один метод – метод Эйлера, который позволяет вычислять выходное значение динамического звена заранее (за шаг до выдачи данного сигнала на выход) и тем самым не образует алгебраических петель. В данном случае получение высокой точности вычислении связано с сильным уменьшением шага метода, что может привести к значительным вычислительным

Методы дифференцирования

Уравнение дифференцирующего динамического звена имеет следующий вид:

.

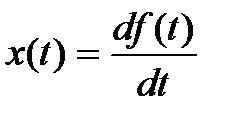Дифференцирование функции производится в соответствии с формулой разностного отношения:

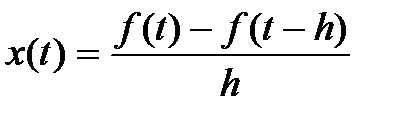,                             (2.32)

где 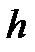 - шаг моделирование.

Заметим, что дифференциал функции не может быть рассчитан в нулевой момент времени.

Модель передаточной функции общего вида

Общая передаточная функция представляется в виде

.

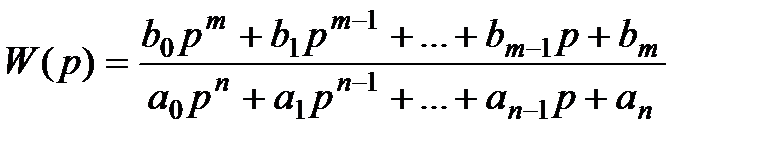Ей соответствует ДУ

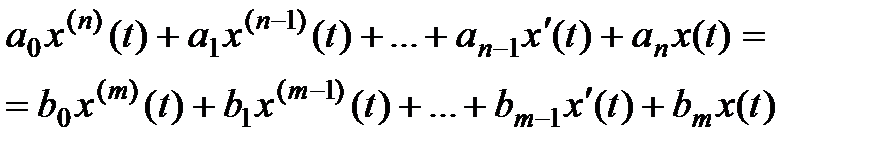.           (2.33)

    Для решения данного уравнения с помощью одного из методов интегрирования оно приводится к эквивалентной системе ДУ, представленных в форме Коши:

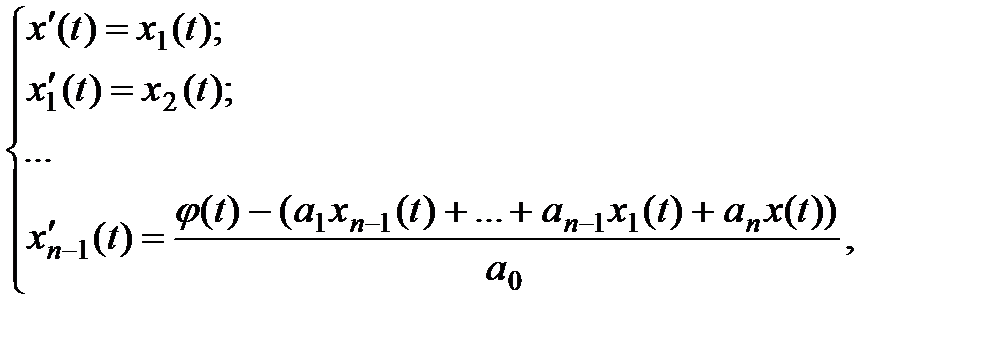              (2.34)

где .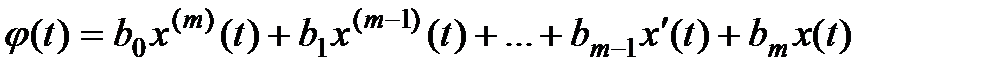

Модель звена запаздывания

Звено запаздывания описывается уравнением

,

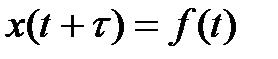где 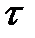- время запаздывания.

Его реализация основана на запоминании поступающих на вход блока значений. Как только модельное время достигнет времени 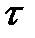, производится выборка заранее сохраненных значений.

Заметим, что запрашиваемое системой моделирования значение выходного сигнала во время t, может лежать между сохраненными значениями. В данном случае используется метод линейной интерполяции для нахождения значения выхода блока.