C истема моделирования и оптимизации
Сложных динамических систем
УЧЕБНОЕ ПОСОБИЕ
Григорьев В.А.
Марголис Д. Б.
Тверь 2012
Оглавление
Введение. 6
1 Обзор систем моделирования динамических систем. 9
1.1 Математическое моделирование. 9
1.2 Понятие простой динамической системы.. 10
1.3 Сложная динамическая система. 11
1.3.1 Структурно-сложная динамическая система. 11
1.3.2 Поведенческая сложность динамической системы.. 15
1.3.3 Структурно-сложная гибридная система. 16
1.4 Имитационное моделирование. 17
1.5 Пакеты визуального моделирования. 18
1.6 Обзор пакетов моделирования. 19
1.7 Система моделирования MatLab. 23
1.8 Система моделирования МВТУ.. 24
2 Математическое и алгоритмическое обеспечение системы моделирования динамических систем. 27
2.1 Математическое описание простой непрерывной динамической системы 27
2.2 Идентификация динамической системы.. 31
2.2.1 Представление динамической системы в системе моделирования 31
2.2.2 Определение внутренних координат системы.. 33
2.2.3 Формирование структурной матрицы системы.. 34
2.3 Получение переходного процесса аналитическим способом. 35
2.3.1 Расчет общей передаточной функции системы.. 35
2.3.2 Переход к полиномиальной форме представления передаточной функции 38
2.3.3 Получение аналитической функции переходного процесса. 39
2.4 Моделирование непрерывных динамических систем. 44
2.4.1 Численные методы решения дифференциальных уравнений. 45
2.4.2 Решатели моделирующих программ. 46
2.4.3 Методы дифференцирования. 47
2.4.4 Модель передаточной функции общего вида. 47
2.4.5 Модель звена запаздывания. 48
2.5 Моделирование дискретных динамических систем. 48
2.5.1 Моделирование дискретных событий. 48
2.5.2 Модель экстраполятора 0-го порядка. 49
2.6 Оптимизация. 49
2.6.1 Методы безусловной оптимизации. 51
2.6.2 Метод Хука-Дживса. 54
2.6.3 Метод Нелдера-Мида. 56
2.6.4 Условная оптимизация. 58
2.6.5 Нахождение глобального минимума целевой функции. 60
3 Разработка системы моделирования сложных динамических систем. 64
3.1 Требования к функциям системы.. 64
3.2 Требования к характеристикам системы.. 65
3.3 Требования к архитектуре системы.. 67
3.4 Выбор средств реализации системы.. 68
3.5 Объектно-ориентированное моделирование. 69
3.6 Проектирование системы на языке UML. 70
3.6.1 Диаграмма вариантов использования. 70
3.6.2 Диаграмма классов. 71
3.6.3 Диаграмма состояний. 74
3.6.4 Диаграмма реализации. 74
3.7 Архитектура и функциональные возможности системы.. 75
3.7.1 Рабочее пространство системы.. 76
3.7.2 Графический редактор моделей системы.. 78
3.7.3 Подсистема представления результатов. 79
3.7.4 Библиотека типовых блоков. 80
3.7.5 Математическое ядро. 81
3.7.6 Система помощи. 83
3.8 Сравнение с ПК «МВТУ». 84
4 Тестирование разработанной системы моделирования. 86
4.1 Имитационное моделирование линейной непрерывной САР. 86
4.2 Оптимизация линейной непрерывной САР. 88
4.3 Анализ линейной непрерывной САР. 90
Заключение. 95
Приложение 1. Руководство пользователя. 97
Приложение 2. Библиотека блоков. 114
Приложение 3. Руководство администратора. 142
Приложение 4. Руководство по установке. 146
Список литературы.. 147
Введение
Имитационное моделирование на цифровых вычислительных машинах является одним из наиболее мощных средств исследования, в частности, сложных динамических систем. Как и любое компьютерное моделирование, оно дает возможность проводить вычислительные эксперименты с еще только проектируемыми системами и изучать системы, натурные эксперименты с которыми, из-за соображений безопасности или дороговизны, не целесообразны. В тоже время, благодаря своей близости по форме к физическому моделированию, это метод исследования доступен более широкому кругу пользователей.
В настоящее время, когда компьютерная промышленность, предлагает разнообразнейшие средства моделирования, любой квалифицированный инженер, технолог или менеджер должен уметь уже не просто моделировать сложные объекты, а моделировать их с помощью современных технологий, реализованных в форме графических сред или пакетов визуального моделирования.
На данный момент тема имитационного моделирования является достаточно изученной, существует много пакетов имитационного моделирования промышленного качества. Существует большое количество литературы, освещающей вопросы применения данных пакетов. Тем не менее, применение конкретных численных методов при реализации систем моделирования, описано не достаточно, что затрудняет разработку аналогов таких систем.
Не все существующие системы моделирования в полной мере отвечают требованиям, связанным с использованием данных систем в процессе высшего обучения в технических ВУЗах. Отрицательные черты данных пакетов с точки зрения использования их в образовательном процессе обусловлены в первую очередь их коммерческой направленностью. Зачастую избыточность функциональных возможностей данных систем моделирования приводит к сложности и трудоемкости их изучения. Также минусом является закрытость математических ядер и невозможность их изучения и модернизации. Еще одним препятствием для изучения может быть отсутствие грамотной локализации самой программы и документации к ней.
Таким образом, представляется актуальным создание свободно распространяемой некоммерческой системы моделирования с открытым исходным кодом, которая бы учитывала специфику использования в образовательном процессе.
Целью работы является разработка программного обеспечения для проведения визуального моделирования, анализа и оптимизации сложных динамических систем.
Для достижения данной цели необходимо решить следующие задачи:
1) провести анализ существующих систем моделирования;
2) формирование требований к инструментарию;
3) разработка алгоритмического обеспечения;
4) разработка архитектуры программного обеспечения;
5) реализация программного обеспечения;
6) исследование разработанного программного обеспечения.
Объектом исследования в данной работе является моделирование динамических систем.
Предметом исследования является методы разработки программного обеспечения для визуального моделирования и оптимизации динамических систем.
Практическая ценность работы заключается в разработке алгоритмического и программного обеспечения для системы моделирования и оптимизации сложных динамических систем.
Разработанная система направлена на обучение студентов по дисциплинам «Основы теории управления», «Моделирование» на кафедре ЭВМ ТГТУ. Она была апробирована на кафедре ЭВМ ТГТУ.
В первой главе работы дается понятие простой и сложной динамической системы, понятие имитационного моделирования. Также здесь проводится анализ существующих средств визуального имитационного моделирования, выявляются их достоинства и недостатки.
Во второй главе описывается теоретическая база исследования, рассматриваются методы математической формализации, а также численные методы моделирования и оптимизации сложных динамических систем.
В третьей главе описываются конкретные этапы разработки программного обеспечения, его архитектура, используемые технологии.
В четвертой главе проводится постановка и выполнение вычислительного эксперимента с использованием разработанного инструментария. Описывается порядок проведения эксперимента, проводится непосредственно эксперимент и делается анализ его результатов.
1
Имитационное моделирование
Имитационное моделирование — это частный случай математического моделирования. Существует класс объектов, для которых по различным причинам не разработаны аналитические модели, либо не разработаны методы решения полученной модели. В этом случае математическая модель заменяется имитатором или имитационной моделью.
К имитационному моделированию прибегают, когда:
· дорого или невозможно экспериментировать на реальном объекте;
· невозможно построить аналитическую модель: в системе есть время, причинные связи, последствие, нелинейности, стохастические (случайные) переменные, дискретные события;
· необходимо сымитировать поведение системы во времени.
Цель имитационного моделирования состоит в воспроизведении поведения исследуемой системы на основе результатов анализа наиболее существенных взаимосвязей между ее элементами или другими словами — разработке симулятора (англ. «simulation modeling») исследуемой предметной области для проведения различных экспериментов. Надо отметить, что если в английском языке термин имеет вполне четкий смысл, ибо симуляция и моделирование не являются синонимами, то по-русски имитационная модель - это нонсенс. Любая модель, в принципе, имитационная, ибо она имитирует реальность.
Указывая, что данная модель имитационная, обычно подчеркивается, что в отличие от других типов абстрактных моделей, в этой модели сохранены и легко узнаваемы такие черты моделируемого объекта, как структура, связи между компонентами, способ передачи информации. С имитационными моделями также обычно связывают и требование иллюстрации их поведения с помощью принятых в данной прикладной области, графических образов.
С учетом последнего замечания, имитационная модель рассматривается как специальная форма математической модели, в которой:
· декомпозиция системы на компоненты производится с учетом структуры проектируемого или изучаемого объекта;
· в качестве законов поведения, могут использоваться экспериментальные данные, полученные в результате натурных экспериментов;
· поведение системы во времени иллюстрируется заданными динамическими образами.
Обзор пакетов моделирования
В настоящее время существует великое множество визуальных средств моделирования. Для формирования требований к разрабатываемой системе моделирования, определения набора необходимых функций системы, а также анализа эффективности разработанной системы необходимо провести обзор существующих пакетов моделирования динамических систем.
В данной работе не рассматриваются пакеты, ориентированные на узкие прикладные области (электроника, электромеханика и т.д.), поскольку элементы сложных систем относятся, как правило, к различным прикладным областям. Среди оставшихся универсальных пакетов (ориентированных на определенную математическую модель), также не рассматриваются пакеты, ориентированные на математические модели, отличные от простой динамической системы (уравнения в частных производных, статистические модели), а также на чисто дискретные. Таким образом, предметом рассмотрения будут универсальные пакеты, позволяющие моделировать структурно-сложные гибридные системы.
Их можно условно разделить на три группы:
1) пакеты "блочного моделирования";
2) пакеты "физического моделирования";
3) пакеты, ориентированные на схему гибридного автомата.
Это деление является условным прежде всего потому, что все эти пакеты имеют много общего: позволяют строить многоуровневые иерархические функциональные схемы, поддерживают в той или иной степени технологию ООМ, предоставляют сходные возможности визуализации и анимации. Отличия обусловлены тем, какой из аспектов сложной динамической системы сочтен наиболее важным.
Пакеты "блочного моделирования" ориентированы на графический язык иерархических блок схем. Элементарные блоки являются либо предопределенными, либо могут конструироваться с помощью некоторого специального вспомогательного языка более низкого уровня. Новый блок можно собрать из имеющихся блоков с использованием ориентированных связей и параметрической настройки. В число предопределенных элементарных блоков входят чисто непрерывные, чисто дискретные и гибридные блоки.
К достоинствам этого подхода следует отнести, прежде всего, чрезвычайную простоту создания не очень сложных моделей даже не слишком подготовленным пользователем. Другим достоинством является эффективность реализации элементарных блоков и простота построения эквивалентной системы. В то же время при создании сложных моделей приходится строить довольно громоздкие многоуровневые блок-схемы, не отражающие естественной структуры моделируемой системы.
Наиболее известными представителями пакетами "блочного моделирования" являются:
· подсистема Simulink пакета Matlab;
· Easy5 (Boeing);
· подсистема SystemBuild пакета Matrixx;
· VisSim.
Пакеты "физического моделирования" позволяют использовать неориентированные и потоковые связи. Непрерывная составляющая поведения элементарного блока задается системой алгебро-дифференциальных уравнений и формул. Дискретная составляющая задается описанием дискретных событий (события задаются логическим условием или являются периодическими), при возникновении которых могут выполняться мгновенные присваивания переменным новых значений. Дискретные события могут распространяться по специальным связям. Изменение структуры уравнений возможно только косвенно через коэффициенты в правых частях (это обусловлено необходимостью символьных преобразований при переходе к эквивалентной системе).
Подход очень удобен и естественен для описания типовых блоков физических систем. Недостатками являются необходимость символьных преобразований, что резко сужает возможности описания гибридного поведения, а также необходимость численного решения большого числа алгебраических уравнений, что значительно усложняет задачу автоматического получения достоверного решения.
К пакетам "физического моделирования" следует отнести:
· 20-SIM;
· Dymola;
· Omola, OmSim;
Как обобщение опыта развития систем этого направления международной группой ученых разработан язык Modelica предлагаемый в качестве стандарта при обмене описаниями моделей между различными пакетами.
Пакеты, основанные на использовании схемы гибридного автомата, позволяют очень наглядно и естественно описывать гибридные системы со сложной логикой переключений. Необходимость определения эквивалентной системы при каждом переключении заставляет использовать только ориентированные связи. Пользователь может сам определять новые классы блоков. Непрерывная составляющая поведения элементарного блока задается системой алгебро-дифференциальных уравнений и формул. К недостаткам следует также отнести избыточность описания при моделировании чисто непрерывных систем.
К этому направлению относится пакет Shift, а также отечественный пакет Model Vision Studium . Пакет Shift в большей стпени ориентирован на описание сложных динамических структур, а пакет MVS – на описание сложных поведений.
Также следует отметить, что системы моделирования отличаются по стоимости приобретения: существуют коммерческие и свободно распространяемые системы.
Цели создания разрабатываемой системы моделирования и ее практическая направленность на моделирование структурно-сложных динамических систем позволяют отнести ее к классу пакетов «блочного моделирования».
Исходя из этого, для более тщательного исследования были выбраны 2 пакета визуального моделирования – подсистема Simulink пакета Matlab и программный комплекс «МВТУ» – как наиболее яркие представители коммерческих и бесплатных систем. Выбор данных систем также обусловлен легкой возможностью получения демонстрационных версий систем для изучения.
Данные системы будут являться аналогами разрабатываемой системы моделирования и подробно рассматриваются в следующих разделах главы.
Система моделирования МВТУ
Программный комплекс «МВТУ» предназначен для исследования динамики и проектирования самых разнообразных систем и устройств. По своим возможностям он является альтернативой аналогичным зарубежным программным продуктам Simulink, VisSim и др. Редактор структурных схем, обширная библиотека типовых блоков и встроенный язык программирования позволяют реализовывать модели практически любой степени сложности, обеспечивая при этом наглядность их представления. ПК «МВТУ» успешно применяется для проектирования систем автоматического управления, следящих приводов и роботов-манипуляторов, ядерных и тепловых энергетических установок, а также для решения нестационарных краевых задач (теплопроводность, гидродинамика и др.). Широко используется в учебном процессе, позволяя моделировать различные явления в физике, электротехнике, в динамике машин и механизмов, в астрономии и т.д. Может функционировать в многокомпьютерных моделирующих комплексах, в том числе и в режиме удаленного доступа к технологическим и информационным ресурсам.
ПК «МВТУ» реализует следующие режимы работы:
1) «МОДЕЛИРОВАНИЕ», обеспечивающий:
· моделирование процессов в непрерывных, дискретных и гибридных динамических системах, в том числе и при наличии обмена данными с внешними программами и устройствами;
· редактирование параметров модели в режиме «on-line»;
· расчет в реальном времени или в режиме масштабирования модельного времени;
· статистическую обработку сигналов, основанную на быстром преобразовании Фурье.
2) «ОПТИМИЗАЦИЯ», позволяющий решать задачи:
· минимизации (максимизации) заданных показателей качества;
· нахождения оптимальных параметров проектируемой системы в многокритериальной постановке при наличии ограничений на показатели качества и оптимизируемые параметры.
3) «АНАЛИЗ», обеспечивающий:
· расчет и построение частотных характеристик и годографов;
· расчет передаточных функций, их полюсов и нулей;
· реализацию метода D-разбиения на плоскости одного комплексного параметра.
4) «СИНТЕЗ», позволяющий конструировать регуляторы:
· по заданным желаемым частотным характеристикам;
· по заданному расположению доминирующих полюсов.
5) «КОНТРОЛЬ И УПРАВЛЕНИЕ», позволяющий создавать виртуальные аналоги:
· пультов управления с измерительными приборами и управляющими устройствами;
· мнемосхем с мультимедийными и анимационными эффектами.
К достоинствам ПК «МВТУ» относятся:
· открытость за счет встроенного языка и реализации нескольких механизмов обмена данными с внешними программами;
· простота построения сложных моделей благодаря использованию вложенных структур, векторизации сигналов и алгоритмов типовых блоков, удобным средствам задания параметров и уравнений;
· эффективные численные методы;
· большое число обучающих и демонстрационных примеров с подробными комментариями.
Для отечественных пользователей удобство работы с ПК «МВТУ» обусловлено также русскоязычным интерфейсом и наличием обширной документации на русском языке. Учебная и демонстрационная версии ПК «МВТУ» вместе с полной документацией и набором демонстрационных примеров распространяются свободно. В учебной версии есть ограничения на сложность модели: порядок дифференциальных уравнений не выше 30, а число блоков не более 100. В демонстрационной версии таких ограничений нет, но модель нельзя сохранить.
К недостаткам рассматриваемого пакета можно отнести слабую реализацию редактора моделей и неоправданная сложность для пользователя некоторых действий с системой (например, проведение частотного анализа).
Метод Эйлера
Метод Эйлера является простейшим методом интегрирования. Его суть заключается в том, что по известной производной 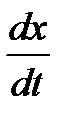 в момент времени
в момент времени 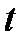 рассчитывается значение функции
рассчитывается значение функции 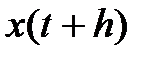 , где
, где 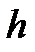 – шаг интегрирования:
– шаг интегрирования:
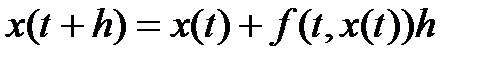 . (2.30)
. (2.30)
Геометрической интерпретацией метода Эйлера является построение ломаной прямой искомой функции (рис. 2.4).
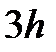
|
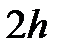
|
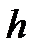
|
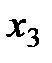
|
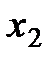
|
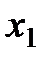
|
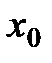
|
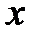
|
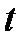
|
Рис. 2.4 Геометрическая интерпретация метода Эйлера
Метод Эйлера – единственный метод, который позволяет заранее (за шаг) рассчитать значение искомой функции, но он обладает самой большой ошибкой
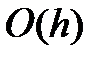 - первый порядок ошибки.
- первый порядок ошибки.
2.4.1.2 Метод трапеций (метод Хьюна)
Метод трапеций является модификацией метода Эйлера и использует 2 значения входной функции для расчета интеграла. Итерационная формула метода выглядит так:
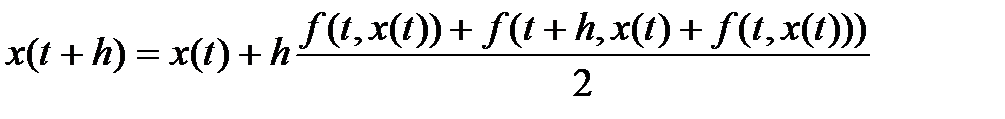 . (2.31)
. (2.31)
Метод трапеций обладает ошибкой второго порядка - 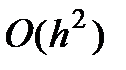 .
.
Методы дифференцирования
Уравнение дифференцирующего динамического звена имеет следующий вид:
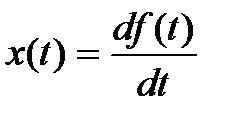 .
.
Дифференцирование функции производится в соответствии с формулой разностного отношения:
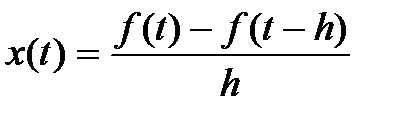 , (2.32)
, (2.32)
где 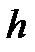 - шаг моделирование.
- шаг моделирование.
Заметим, что дифференциал функции не может быть рассчитан в нулевой момент времени.
Модель звена запаздывания
Звено запаздывания описывается уравнением
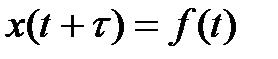 ,
,
где 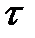 - время запаздывания.
- время запаздывания.
Его реализация основана на запоминании поступающих на вход блока значений. Как только модельное время достигнет времени 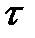 , производится выборка заранее сохраненных значений.
, производится выборка заранее сохраненных значений.
Заметим, что запрашиваемое системой моделирования значение выходного сигнала во время t, может лежать между сохраненными значениями. В данном случае используется метод линейной интерполяции для нахождения значения выхода блока.
Оптимизация
Оптимизация динамических систем является важной частью моделирующих программ, и ее реализация позволяет значительно увеличить полезность разрабатываемого инструментария.
Оптимизация динамической системы подразумевает нахождение таких ее параметров, которые минимизируют (максимизируют) определенные динамические свойства или характеристики системы. Примером оптимизации динамической системы является нахождение оптимальных настроек регулятора САР, которые позволяют достигнуть наилучшего качества переходного процесса (перерегулирование, время регулирования и т. д.)
В общем случае постановка задачи оптимизации содержит:
· Целевую функцию 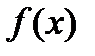 , где
, где 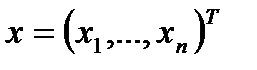 , определенную на n-мерном евклидовом пространстве
, определенную на n-мерном евклидовом пространстве 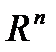 . Ее значения характеризуют степень достижения цели, во имя которой поставлена и решается задача;
. Ее значения характеризуют степень достижения цели, во имя которой поставлена и решается задача;
· Множество допустимых решений 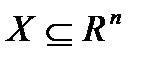 , среди элементов которого осуществляется поиск.
, среди элементов которого осуществляется поиск.
Требуется найти такой вектор 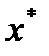 из множества допустимых решений, которому соответствует минимальное значение целевой функции на этом множестве:
из множества допустимых решений, которому соответствует минимальное значение целевой функции на этом множестве:
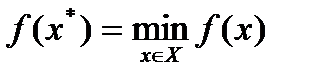 .
.
Задача поиска максимума функции 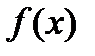 сводится к задаче поиска минимума путем замены знака перед функцией на противоположный:
сводится к задаче поиска минимума путем замены знака перед функцией на противоположный:
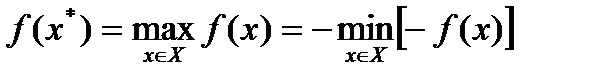 .
.
Задача поиска минимума и максимума целевой функции 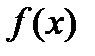 называется задачей поиска экстремума:
называется задачей поиска экстремума:
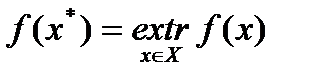 .
.
Точка 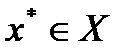 называется точкой глобального минимума функции
называется точкой глобального минимума функции 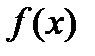 на множестве
на множестве 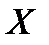 , если функция достигает в этой точке своего наименьшего значения, т.е.
, если функция достигает в этой точке своего наименьшего значения, т.е.
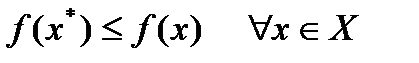 . (2.35)
. (2.35)
Точка 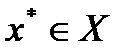 называется точкой локального минимума функции
называется точкой локального минимума функции 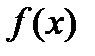 на множестве
на множестве 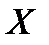 , если существует
, если существует 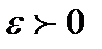 , такое, что если
, такое, что если 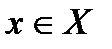 и
и 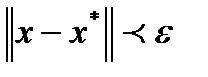 , то
, то 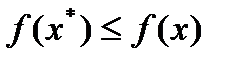 . Здесь
. Здесь 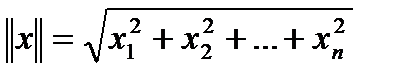 - эвклидова норма вектора
- эвклидова норма вектора 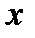 .
.
Если множество допустимых решений 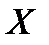 задается ограничениями (условиями), накладываемыми на вектор
задается ограничениями (условиями), накладываемыми на вектор 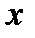 , то решается задача поиска условного экстремума (условная оптимизация).
, то решается задача поиска условного экстремума (условная оптимизация).
Если 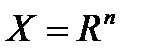 , т.е. ограничения на вектор
, т.е. ограничения на вектор  отсутствуют, решается задача поиска безусловного экстремума (безусловная оптимизация).
отсутствуют, решается задача поиска безусловного экстремума (безусловная оптимизация).
Для решения задачи поиска экстремума функции используются различные методы оптимизации, которые будут рассмотрены в следующих разделах.
Метод Хука-Дживса
Суть этого метода состоит в следующем. Задаются некоторой начальной точкой 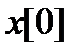 . Изменяя компоненты вектора
. Изменяя компоненты вектора 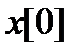 , обследуют окрестность данной точки, в результате чего находят направление, в котором происходит уменьшение минимизируемой функции
, обследуют окрестность данной точки, в результате чего находят направление, в котором происходит уменьшение минимизируемой функции 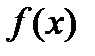 . В выбранном направлении осуществляют спуск до тех пор, пока значение функции уменьшается. После того как в данном направлении не удается найти точку с меньшим значением функции, уменьшают величину шага спуска. Если последовательные дробления шага не приводят к уменьшению функции, от выбранного направления спуска отказываются и осуществляют новое обследование окрестности и т. д.
. В выбранном направлении осуществляют спуск до тех пор, пока значение функции уменьшается. После того как в данном направлении не удается найти точку с меньшим значением функции, уменьшают величину шага спуска. Если последовательные дробления шага не приводят к уменьшению функции, от выбранного направления спуска отказываются и осуществляют новое обследование окрестности и т. д.
Исходными данными для работы метода являются:
1) 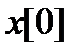 – вектор начальных значений;
– вектор начальных значений;
2) d – начальный шаг поиска;
3) 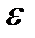 – минимальный шаг поиска.
– минимальный шаг поиска.
Ниже представлена блок-схема алгоритма метода Хука-Дживса.
| Нет |
| Да |
| Да |
| Нет |
| h < e |
| h = h / 5 |
| fk < fb |
| Исследование в точке xb (шаг h): xk, fk = f(xk) |
| xb=x[0] fb = f(xb) |
| Ввод x[0], d, e |
| Начало |
| xb = xk h = h / 5 |
| Нет |
| xb = xk2 xk = xk3 fb = fk = xk3 |
| Да |
| xk3 < xk2 |
| Выход |
| Вывод xb |
| xb = xk |
| Исследование в точке xk2 (шаг h): xk3, fk3 = f(xk3) |
| xk2 = 2xk-xb fk2 = f(xk2) |
Рис. 2.6 Блок-схема алгоритма метода Хука-Дживса
Заметим, что величина уменьшение шага в 5 раз выбрана экспериментальным путем, ее изменение может привести к увеличению или уменьшению скорости сходимости метода в зависимости от решаемой задачи.
Метод Нелдера-Мида
Данный метод состоит в том, что для минимизации функции n переменных 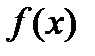 в n-мерном пространстве строится многогранник, содержащий (n + 1) вершину. Очевидно, что каждая вершина соответствует некоторому вектору х. Вычисляются значения целевой функции
в n-мерном пространстве строится многогранник, содержащий (n + 1) вершину. Очевидно, что каждая вершина соответствует некоторому вектору х. Вычисляются значения целевой функции 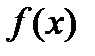 в каждой из вершин многогранника, определяются максимальное из этих значений и соответствующая ему вершина
в каждой из вершин многогранника, определяются максимальное из этих значений и соответствующая ему вершина 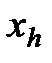 , минимальное (вершина
, минимальное (вершина 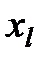 ) и значение следующее за наибольшим (вершина
) и значение следующее за наибольшим (вершина 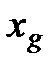 ). Через
). Через 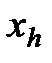 и центр тяжести остальных вершин
и центр тяжести остальных вершин 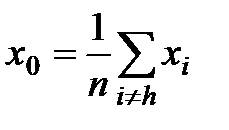 проводится проецирующая прямая, на которой находится точка с меньшим значением целевой функции, чем в вершине
проводится проецирующая прямая, на которой находится точка с меньшим значением целевой функции, чем в вершине 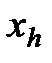 . Затем из многогранника исключается вершина
. Затем из многогранника исключается вершина 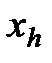 . Из оставшихся вершин и полученной точки строится новый многогранник, с которым повторяется описанная процедура.
. Из оставшихся вершин и полученной точки строится новый многогранник, с которым повторяется описанная процедура.
В процессе выполнения данных операций многогранник изменяет свои размеры и форму в соответствии с тремя операциями: отражение, растяжение, сжатие.
Точку 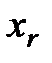 расчитывают как отражение
расчитывают как отражение 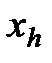 относительно
относительно 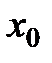 :
:
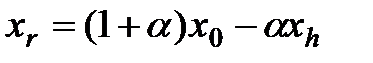 ,
,
где 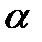 – коэффициент отражение. Обычно
– коэффициент отражение. Обычно 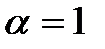 .
.
Точку 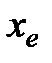 расчитывают как растяжение
расчитывают как растяжение 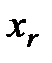 относительно
относительно 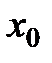 :
:
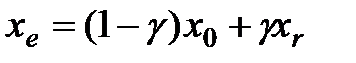 ,
,
где 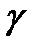 – коэффициент растяжения. Обычно
– коэффициент растяжения. Обычно 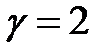 .
.
Точку 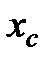 расчитывают сжатие
расчитывают сжатие 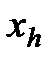 относительно
относительно 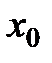 :
:
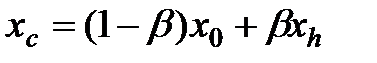 ,
,
где 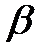 – коэффициент сжатия. Обычно
– коэффициент сжатия. Обычно 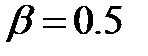 .
.
При невозможности получить уменьшения значения функции симплекс сжимается в 2 раза вокруг точки 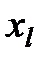 по формуле:
по формуле:
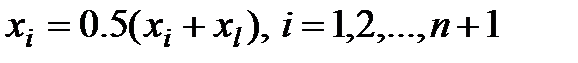
Проверка сходимости метода использует не разницу между значениями фукнций 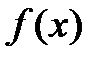 или векторов
или векторов 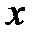 на соседних итерациях, а стандартное отклонение значений функций в вершинах симплекса (многогранника):
на соседних итерациях, а стандартное отклонение значений функций в вершинах симплекса (многогранника):
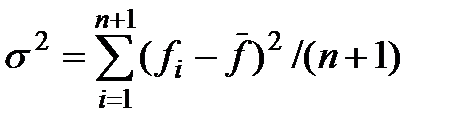 , где
, где 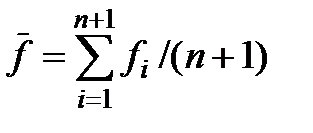 .
.
Считается, что работа метода завершена при  , где
, где 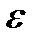 – минимальное стандартное отклонение метода.
– минимальное стандартное отклонение метода.
Блок-схема работы алгоритма Нелдера-Мида представлена на рис. 2.7
| Да |
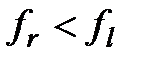
|
Найти 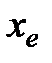 , , 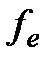
|
| Да |
| Нет |
| Нет |
| Да |
| Да |
| Нет |
| Да |
| Нет |
| Нет |
| Да |
| Нет |
Заменить
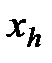 на на 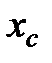
|
Заменить
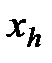 на на 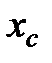
|
|
Найти  , , 
|
|
|
Заменить  на на 
|
|
| Конец |
| Проверка сходимости |
Рассчет 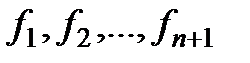
|
Заменить 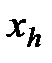 на на 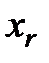
|
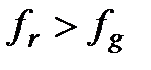
|
Найти 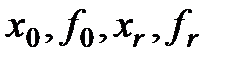
|
Найти
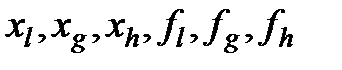
|
Рассчет
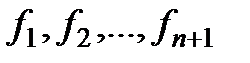
|
Ввод x[0], 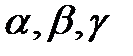 , e , e
|
| Начало |
Рис. 2.7 Блок-схема алгоритма метода Нелдера-Мида
Условная оптимизация
В реальных условиях на переменные 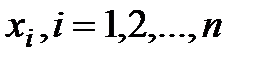 , и некоторые функции
, и некоторые функции  ,
, 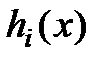 , характеризующие качественные свойства объекта, системы, процесса, могут быть наложены ограничения (условия) вида:
, характеризующие качественные свойства объекта, системы, процесса, могут быть наложены ограничения (условия) вида:
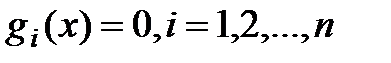 ;
;
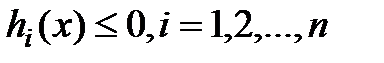 ; (2.39)
; (2.39)
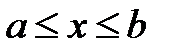 .
.
Такую задачу называют задачей условной оптимизации.
Каждая точка х в n-мерном пространстве переменных 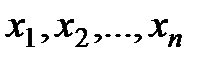 , в которой выполняются ограничения, называется допустимой точкой задачи. Множество всех допустимых точек называют допустимой областью G. Решением задачи (оптимальной точкой) называют допустимую точку х*, в которой целевая функция
, в которой выполняются ограничения, называется допустимой точкой задачи. Множество всех допустимых точек называют допустимой областью G. Решением задачи (оптимальной точкой) называют допустимую точку х*, в которой целевая функция 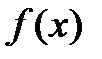 достигает своего минимального значения.
достигает своего минимального значения.
В разработанной системе моделирования реализованна условная оптимизация с ограничениями только одного вида: 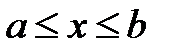 .
.
Решение поставленной задачи может быть достигнуто двумя способами:
1) Прямая проверка ограничений. Данный метод наиболее прост в реализации. Для этого необходимо при решении задачи оптимизации присвоить целевой функции очень большое значение там, где ограничения нарушаются. График зависимости целевой функции одной переменной 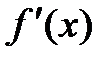 при использовании данного метода показан на рис. 2.8.
при использовании данного метода показан на рис. 2.8.
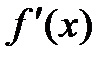
|
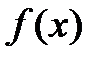
|
| b |
| a |
| Очень большое значение |
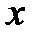
|
Рис. 2.8. Ограничение типа «обрыв»
Данный подход обладает одним недостатком: метод не может двигаться вдоль границы области ограничений и сходимость достигается в первой же точке границы, где и находится решение. Поэтому зачастую для нахождения правильного решения требуются более изощренные процедуры, чем приведенная выше.
Использование штрафных функций. Основная идея метода состоит в преобразовании задачи минимизации функции 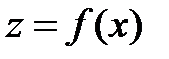 с ограничениями, наложенными на
с ограничениями, наложенными на 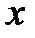 , в задачу поиска минимума без ограничений функции
, в задачу поиска минимума без ограничений функции
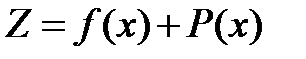 ,
,
где 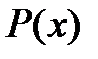 – штрафная функция.
– штрафная функция.
Необходимо, чтобы при нарушении ограничений она «штрафовала» функцию 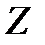 , т. е. увеличивала ее значение. В этом случае минимум
, т. е. увеличивала ее значение. В этом случае минимум 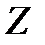 будет находиться внутри области ограничений.
будет находиться внутри области ограничений.
Для ограничения 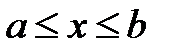 штрафная функция может быть представлена в следующем виде:
штрафная функция может быть представлена в следующем виде:
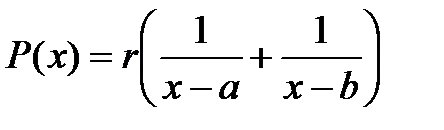 ,
,
где 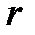 – значение, определяющее крутизну ограничивающих кривых. Обычно
– значение, определяющее крутизну ограничивающих кривых. Обычно 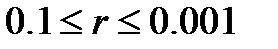 .
.
График зависимости целевой функции одной переменной 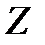 при использовании данного метода показан на рис. 2.9.
при использовании данного метода показан на рис. 2.9.
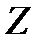
|
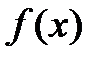
|
| b |
| a |
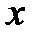
|
Рис. 2.9. Ограничение с использованием штрафных функций
Требования к функциям системы
Разрабатываемая автоматизированная система моделирования должна производить визуальное моделирование, анализ и оптимизацию сложно-структурных динамических систем. Реализация данных основных функций системы подразумевает поддержку системой ряда подфункций.
Для проведения моделирования сложно-структурных динамических систем разрабатываемая система должна:
1) Обеспечивать ввод моделируемой системы в графическом редакторе в виде структурной схемы системы, используя стандартные блоки библиотеки или составные блоки, созданные пользователем;
2) Позволять создавать пользователю сложные составные блоки, используя стандартные блоки библиотеки или другие составные блоки, созданные пользователем без ограничений на уровень вложенности блоков;
3) Позволять пользователю задавать начальные условия для моделирования, в том числе параметры блоков системы, параметры используемых методов моделирования;
4) Позволять пользователю просматривать результаты моделирования в графическом виде.
Для проведения анализа сложно-структурных линейных динамических систем разрабатываемая система должна:
1) Проводить идентификацию моделируемой системы по заданной структурной схеме;
2) Находить общую передаточную функцию системы в полиномиальной форме;
3) Находить аналитическую функцию переходного процесса анализируемой системы;
4) Производить построение частотных характеристик анализируемой системы.
Для проведения оптимизации сложно-структурных динамических систем разрабатываемая система должна:
1) Поддерживать средства для нахождения стандартных критериев качества функционирования динамических систем;
2) Позволять пользователю выбирать один из реализованных методов оптимизации и настраивать его параметры;
3) Производить оптимизацию и представлять пользователю ее результаты в графической форме.
Требования к характеристикам системы
В результате рассмотрения существующих аналогичных пакетов моделирования динамических систем к разрабатываемому программному обеспечению (ПО) можно предъявить следующие общие требования:
1) Наличие развитого графического интерфейса. Он должен гарантировать:
· наглядность создаваемых моделей, процессов и результатов моделирования;
· возможность выполнения большинства операций на всех этапах от начального синтеза модели до анализа полученных результатов без использования алфавитно-цифровой клавиатуры, а при помощи только манипулятора типа “мыши”, что существенно упрощает эксплуатацию системы;
· возможность непосредственного “визуального проектирования” моделей путём манипуляции с пиктограммами без привлечения специальных языков описания моделей, требующих особого изучения, что позволяет значительно сократить время освоения системы и, во многих случаях, затраты времени на подготовку, отладку и документирование моделей.
2) Поддержка иерархии блоков и моделей, которая обеспечивает:
· построение на базе элементарных модельных блоков и структур синтезированных блоков и структур, соответствующих конкретным моделируемым объектам (электродвигатель, регулятор и т.п.), которые в свою очередь также могут использоваться в качестве элементов для построения более укрупненных моделей (производственный участок, устройство и т.п.) и т.д., что позволяет успешно преодолеть модельную сложность реальных динамических объектов;
· формирование библиотек различного уровня модельной иерархии, ориентированных на широкий спектр приложений и различный уровень подготовки пользователя;
· возможность создания модельных библиотек высокого уровня готовности и специализации для конкретных областей применения.
3) Высокая скорость моделирования и оптимизации систем, высокая устойчивость к ошибкам и сбоям.
4) Организация сохранения и открытия моделей.
5) Организация режима «Администратора системы» для углубленных настроек приложения.
Также к системе предъявляются требования, связанные с ее использованием в образовательном процессе:
1) Полнота библиотеки блоков - типовых элементов структуры (ТЭС). Так как создание встроенного языка программирования является достаточно трудоемкой задачей, универсальность системы должна обеспечиваться наличием полной библиотеки с элементами из предметных областей разных дисциплин (основные дисциплины: «Основы теории управления», «Моделирование»).
2) Простота освоения. Скорость и эффективность обучения напрямую зависят от простоты освоения ПО, которая может быть достигнута дружественным интерфейсом, большим количеством примеров, наличием развитой системы помощи содержащей как информацию по работе с ПО, так и теоретические материалы по изучаемым дисциплинам.
Требования к архитектуре системы
Требования к функциональному содержанию системы моделирования порождают требования к архитектуре разрабатываемого ПО. В качестве основных принципов построения пакетов моделирования могут быть названы следующие:
1) чёткая модульная структура;
2) открытая архитектура.
Модульная структура
Разбиение системы на относительно автономные модули с чётко специфицированным интерфейсом полностью соответствует современным технологиям программирования и позволяет обеспечить целый ряд преимуществ:
· снижение порога сложности системы и максимальное распараллеливание работ по её разработке, развитию и сопровождению за счёт независимой разработки и отладки отдельных модулей;
· возможность постепенного развития системы за счет эволюции и замены отдельных модулей;
· вариативность функциональных возможностей, обеспечиваемая возможностью разработки альтернативных наборов модулей соответствующего назначения;
· высокая гибкость и адаптируемость системы за счёт комплектации такими наборами модулей, которые максимально соответствуют текущим требованиям;
· расширение возможностей интеграции системы с другими программными продуктами как за счёт использования различных интерфейсных модулей для связи с внешними системами, так и за счёт независимого использования отдельных модулей в других системах.
Открытость систем
Чёткая спецификация межмодульных интерфейсов позволяет обеспечить их взаимозаменяемость, а также:
· возможность докомплектации системы при необходимости наборами специализированных модулей, дополняющими и оптимизирующими её функциональные характеристики в требуемом направлении;
· возможность разработки сторонними организациями отдельных комплектующих модулей, ориентированных на конкретные приложения, что позволяет существенно расширить потенциальные области применения системы;
· развитие системы непосредственно пользователем путём разработки и совершенствования соответствующих модулей;
· расширение возможностей системы за счёт интеграции в систему внешних программных средств, например, различных редакторов, средств символьной манипуляции, средств визуализации и т.п.
· возможность интеграции отдельных программных модулей системы в другие программные продукты различного назначения.
Диаграмма классов
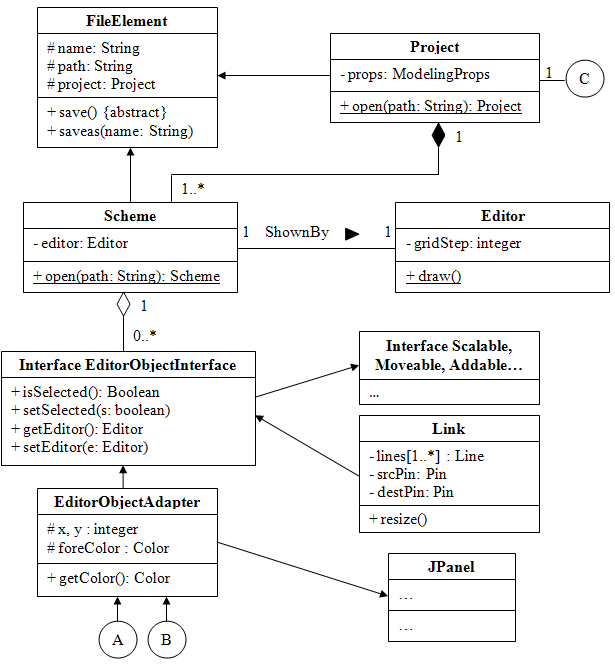
Рис. 3.2. Диаграмма основных классов системы
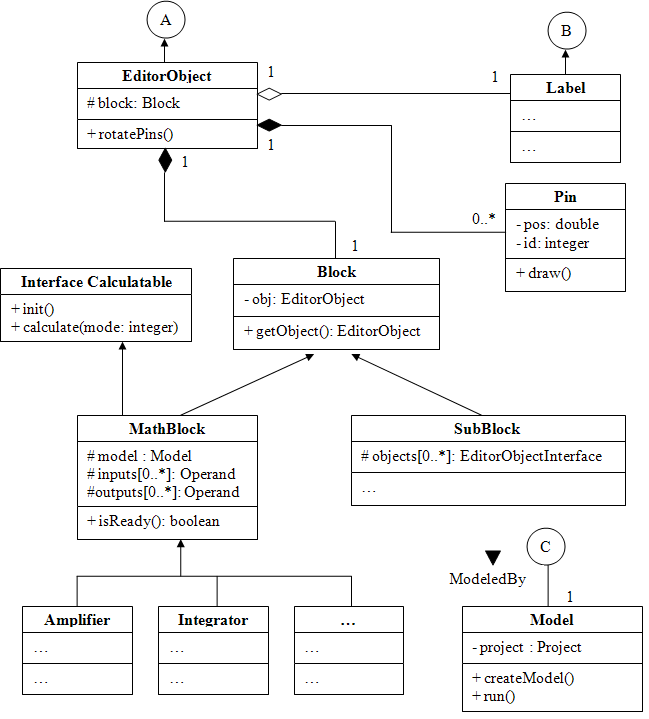
Рис. 3.2. Диаграмма основных классов системы (продолжение)
В системе моделирования динамическая система представлена в качестве проекта (Project). Проект может содержать от одной до нескольких структурных схем (Scheme), связанных между собой внешними сигналами. Каждая структурная схема отображается в окне редактора (Editor).
Каждая схема состоит из визуальных объектов – блоков (EditorObject) и связей между ними (Link). Каждый графический блок инкапсулирует в себе свою математическую сущность:
· MathBlock – родитель для классов объектов библиотеки;
· SubBlock – групповой элемент структуры, содержит подсхему.
Конкретная математическая реализация блока описывается классами-потомками от класса MathBlock: усилитель (Amplifier), интегратор (Integrator) и т.д. Данные классы содержат в себе свои собственные параметры и переопределяют метод calc().
При компиляции каждого проекта создается модель (Model), которая прогоняется для получения определенных динамических характеристик исходной динамической системы.
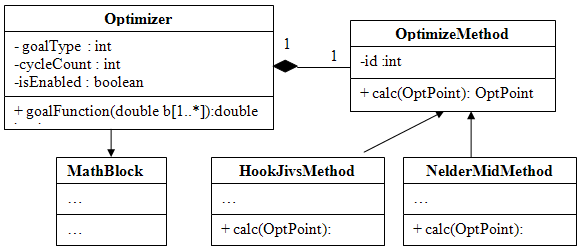
Рис. 3.3. Диаграмма классов системы, участвующих в оптимизации
Оптимизация производится стандартным блоком библиотеки Optimizer, потомком класса MathBlock. Optimizer содержит в себе класс OptimizeMethod, реализация которого определяет конктетный метод оптимизации. Он имеет 2 потомка – классы HookJivsMethod и NelderMidMethod, которые переопределяют его метод calc().
Диаграмма состояний
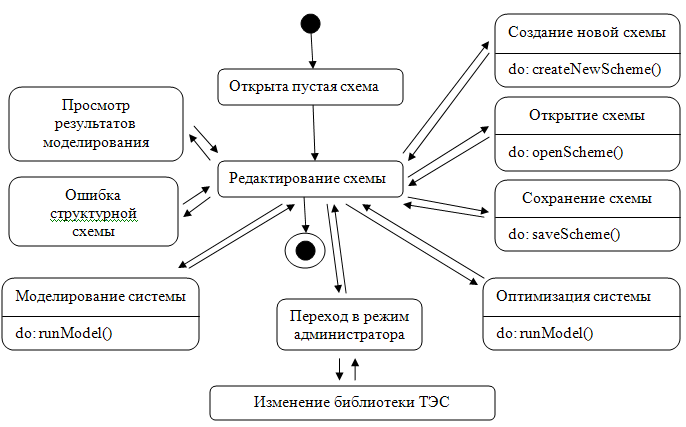
Рис. 3.4. Диаграмма состояний системы
Диаграмма состояний расширяет диаграмму вариантов использования и показывает состояния системы и возможные переходы между ними.
Диаграмма реализации
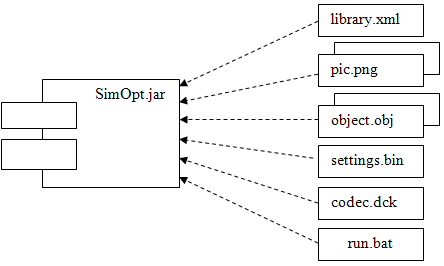
Рис. 3.5. Диаграмма реализации системы
1) model.jar – основной запускаемый модуль программы, исполняемый java-архив. В нем собраны все исходные коды программы. Данный файл может запускаться с помощью java-машины.
2) library.xml – файл, представляющий древовидную структуру библиотеки типовых элементов. Он позволяет отображать элементы библиотеки из программы с помощь пиктограмм, а также задает соответствие этих элементов, файлам, содержащим экземпляры данных объектов.
3) pic.png – набор графических изображений, используемых в программе.
4) object.obj – набор бинарных файлов, представляющих элементы библиотеки типовых элементов.
5) settings.bin – файл общих настроек системы;
6) codec.dck – файл конфигурации рабочего окна системы;
7) run.bat – пакетный файл для быстрого запуска java-архива в java-машине.
Библиотека типовых блоков
Структура библиотеки типовых блоков размещается в файле формата XML, который идеально подходит для хранения древовидных структур. Верхним уровнем иерархии являются разделы блоков, нижним – сами блоки.
Каждая запись о разделе содержит название раздела, рисунок раздела и все блоки, включенные в данный раздел. Каждая запись о блоке содержит название блока, рисунок блока и путь к файлу, непосредственно представляющему данный блок в системе моделирования. Иерархическая структура файла XML библиотеки представлена на рис.3.8.

Рис. 3.8. Представление структуры библиотеки в XML-файле
Отображение данного файла в системе моделирования представлено на рис. 3 приложение 1.
Состав библиотеки типовых элементов подробно описан в приложении 2.
Как видно из рис. 3.8, типовые блоки в системе хранятся не в базе данных, а в файлах. Каждому блоку соответствует один файл.
Рассмотрим принцип формирования файлов, соответствующих типовым блокам. Метод их записи основан на принципе сериализации. Файлы с сериализованными объектами сами по себе содержат иерархическую структуру в формате XML. Сериализация заключается в прямой записи экземпляров классов в файл, причем таким образом, что исключается дублирование ссылок. Другими словами после записи в файл объектов со сложной структурой и перекрестными ссылками по принципу сериализации, их чтение в оперативную память даст тоже состояние объектов в памяти, что и до записи, причем не будет создано повторяющихся объектов.
Использование такого подхода, например, очень упростило сохранение составных блоков (или моделей) системы, которые состоят из множества блоков и связей и имеют большое количество перекрестных ссылок внутри себя.
Таким образом, сохранение измененного блока в память представляет собой не что иное, как перезапись его файла новым образом объекта.
Данный метод имеет и свои недостатки. При использовании стандартной сериализации сохранение графических объектов (наследованных от стандартных классов языка) приводит к получению файлов большого размера.
Еще одним недостатком является невозможность открыть в системе сохраненный блок, если его программная реализация претерпела существенные изменения. Данный объект необходимо переписывать в файл заново.
Математическое ядро
Основной функцией математического ядра является формирование потока исполнения модели на основе ее структурной схемы. Под потоком исполнения понимается порядок вызова вычислительных процедур блоков модели.
При формировании единого потока выполнения встает ряд трудностей, связанных с:
· Наличием составных элементов (ГЭС);
· Наличием разветвителей сигналов (три графические связи относятся к одному и тому же сигналу);
· Наличием нескольких структурных схем одной модели, сигналы между которыми передаются по специальным блокам;
· Наличие циклов (обратные связи).
Проблема циклов разрешается благодаря так называемым блокам с эффектом памяти. К данным блокам относятся интегратор, звено запаздывания, апериодическое звено 1-ого порядка и т.д. Относительно данных блоков действует закон, на данном шаге выходное значение блока не зависит от его входного значения (действительно только при интегрировании по Эйлеру без использования итерационного решателя). Таким образом данные блоки участвуют в потоке исполнения модели дважды: один раз как генераторы сигнала, а второй раз как приемники сигнала.
Принцип решения первых трех трудностей, связан с требованием, чтобы результирующий поток исполнения не содержал не разветвителей, ни портов ГЭС, ни передающих сигналов блоков. То есть из системы на основе связей изымаются данные блоки и происходит переход от графических связей к сигналам. Каждый сигнал имеет уникальный идентификатор. Для реализации данного перехода используется рекурсивный алгоритм.
Пример исходной системы показан на рис. 3.9. Результат работы подобного алгоритма показан на рис. 3.10.
| ГЭС |
| y(t) |
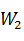
|
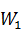
|

| g(t) |
Рис. 3.9 Структурная схема САР
| 5 |
| 5 |
| 4 |
| 3 |
| 2 |
| 1 |
| 2 |
| y(t) |
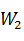
|
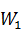
|

| g(t) |
Рис. 3.10 Результирующая схема с сигналами
По результирующей схеме строится «выходная» карта схемы (см. п. 2.2.1). Одновременно при работе рекурсивного алгоритма определяется список блоков генераторов сигнала на основе информации о готовности их выходных сигналов (всегда готовы для выдачи). Данные блоки первыми попадают в итоговый поток исполнения.
Затем для каждого генераторного блока по карте схемы находятся блоки приемники сигнала. Если они готовы для расчета, то они также заносятся в поток и сами попадают в конец списка генераторных блоков. Таким образом все блоки заносятся в результирующий поток причем дважды в него попадают только генераторные блоки.
Система помощи
Учитывая масштаб разработанной системы, стремление при разработке к интуитивно понятному интерфейсу и наглядности, и трудоемкость разработки качественной индексированной службы помощи было решено ее не реализовывать.
Таким образом, система помощи в разработанное приложение не интегрирована и представляет собой несколько руководств по работе с системой моделирования:
1) Руководство пользователя;
2) Руководство администратора;
3) Библиотека блоков;
4) Руководство по установке.
Данные вспомогательные материалы предоставлены в приложении к работе.
Сравнение с ПК «МВТУ»
Разработанную систему моделирования и оптимизации по нескольким критериям можно сравнить с ПК «МВТУ», как с наиболее близким аналогом.
К несомненным преимуществам ПК «МВТУ» над разработанной системой можно отнести:
1) Использование более мощного математического аппарата, реализация итерационного решателя, большое количество методов интегрирования.
2) Наличие встроенного языка программирования, возможность создавать более сложные модели.
3) Более обширная библиотека типовых элементов, хотя применительно к направлению использования разработанного приложения это не сыграет большой роли.
4) Более низкие системные требования.
5) Качественная индексированная система помощи, наличие большого кол-ва справочных материалов.
К преимуществам разработанного ПО можно отнести:
1) Улучшенная организация рабочего пространства системы, удобная и эффективная реализация многооконного режима.
2) Улучшенный редактор схем моделей, более качественное отображение элементов структурных схем.
3) Более высокий общий уровень интерфейса, простота и понятность диалога с пользователем.
4) Наглядность и понятность реализации функций оптимизации и анализа динамических систем, за счет использования блочного подхода.
5) Открытость исходного кода программы.
Заключение
В данной работе была проведена разработка системы моделирования и оптимизации сложных динамических систем.
Для этого был проведен анализ существующих систем моделирования, были выявлены их достоинства и недостатки. На основании данного анализа были выдвинуты требования к разрабатываемому инструментарию. Затем были рассмотрены математические методы моделирования и оптимизации динамических систем и из них были выбраны методы, которые в дальнейшем были реализованы в системе моделирования.
На основании выдвинутых требований была разработана архитектура инструментария и определены его основные функции.
Разработанная архитектура отвечает требованию модульности, так как ее внутренняя программная структура разрабатывалась на основе интерфейсов между различными классами и более крупными частями программ. В созданной системе классов реализовано четкое разделение между графическим представлением объекта и его математической сущностью.
Архитектура также отвечает требованию открытости, разработанные модули могут успешно использоваться при разработке стороннего программного обеспечения, так как система распространяется свободно с открытым программным кодом.
Разработка приложения велась на объектно-ориентированном языке высокого уровня Java.
В системе были использованы свободно распространяемые библиотеки и компоненты, которые позволили ускорить разработку приложения.
По сравнению с другими пакетами моделирования в разработанной системе был качественно улучшен принцип организации рабочего пространства приложения, улучшен редактор моделей, позволяющий более качественно отображать элементы структурных схем.
Для проверки системы были проведены эксперименты по моделированию и оптимизации динамических систем. Было проведено сравнения аналитического метода получения переходного процесса САР и метода пошагового имитационного моделирования, рассчитаны зависимости ошибки моделирования от шага моделирования.
Разработанная система отвечает предъявленным требованиям и может быть использована в образовательном процесс на кафедре ЭВМ ТГТУ для проведения практических занятий по дисциплинам «Основы теории управления» и «Моделирование».
Приложение 1. Руководство пользователя
На рис. 1 изображено основное окно системы моделирования. Оно содержит следующие элементы:
8) Главное меню;
9) Библиотека типовых элементов;
10) Редактор модели;
11) Окно проектов;
12) Консоль;
13) Окно ошибок;
14) Окно свойств объектов.
Все перечисленные окна приложения интегрированы в основное окно. Организация рабочего пространства имеет следующие возможности:
· Динамическое изменение размеров окон, перераспределение места, занимаемого различными окнами;
· Организация окон, размещенных в одном месте рабочего пространства в виде вкладок;
· Создание новых областей для окон, деление старых областей для окон между несколькими окнами.
Все операции над окнами производятся в режиме Drag&Drop. Переработанный интерфейс приложения с помощью перечисленного функционала представлен на рис. 2.
| 7 |
| 3 |
| 2 |
| 4 |
| 5 |
| 1 |
| 6 |
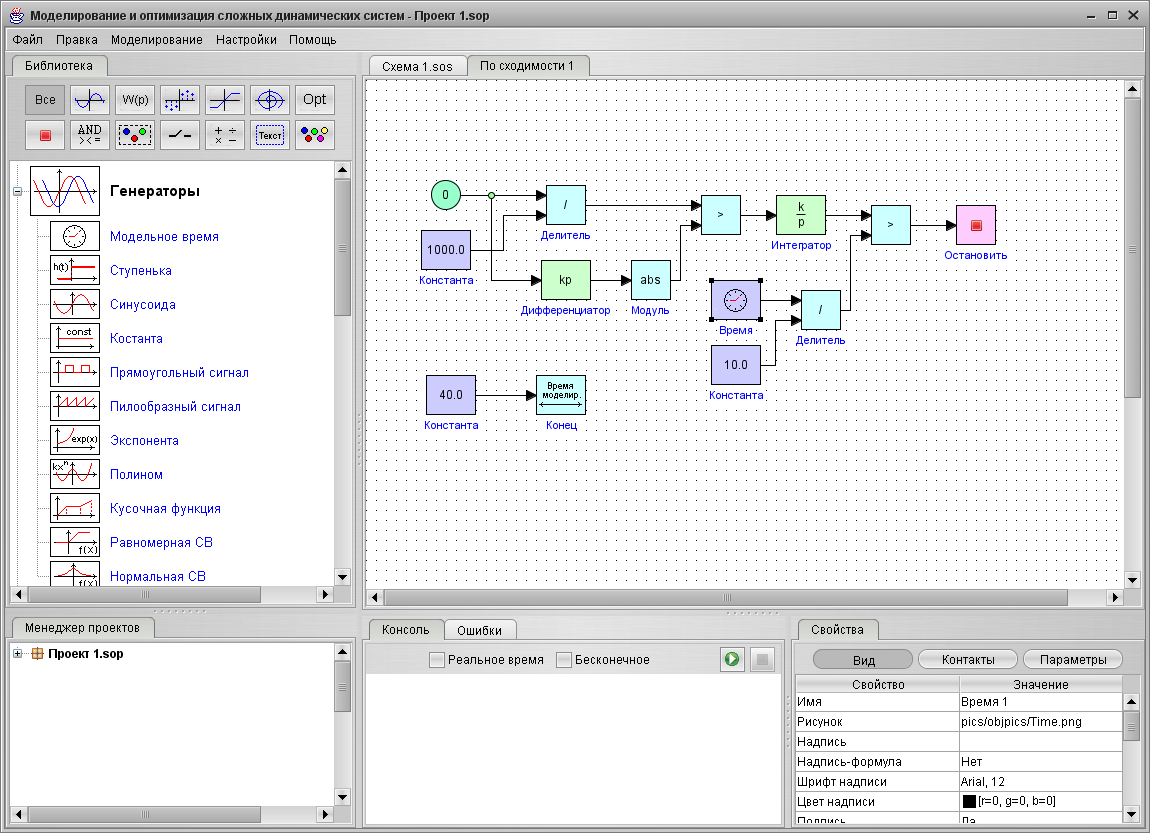
Рис. 1. Главное окно приложения
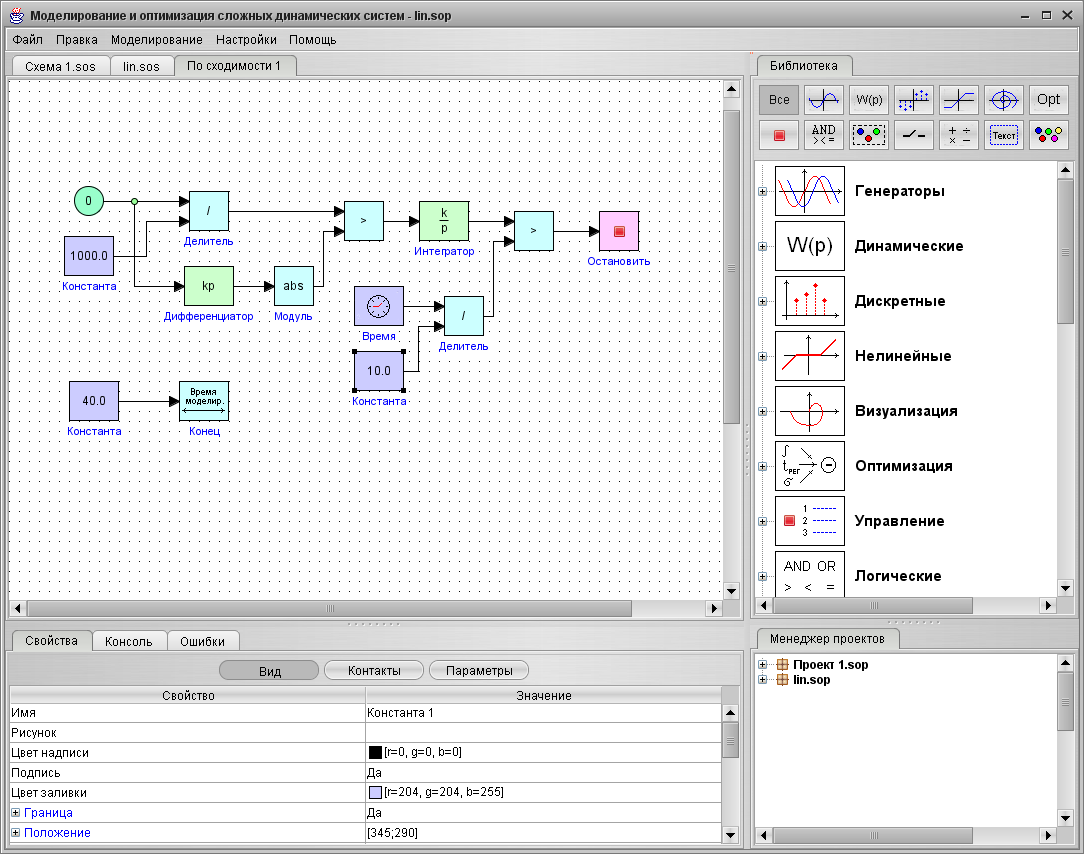
Рис. 2. Изменение организации рабочего пространства приложения
Рассмотрим подробнее перечисленные элементы приложения.
Главное меню
Главное меню содержит 5 основных пунктов:
5) Файл – работа с файлами в системе: открытие, сохранение моделей, закрытие окон и т.д.
6) Правка – работа с графическим редактором моделей: отмена, копирование, удаление и т.д.
7) Моделирование – настройки и непосредственный запуск моделирования.
8) Общие настройки системы – в частности, вход в систему в качестве администратора.
Пункты меню «Файл»:
1. Новый
· Проект – создание нового проекта;
· Схема – создание новой схемы в текущем проекте;
2. Открыть проект – открытие проекта;
3. Сохранить – сохранение текущей схемы ;
4. Сохранить как – сохранение текущей схемы под новым именем;
5. Сохранить проект как – сохранение проекта под новым именем;
6. Сохранить все – сохранить все схемы в проекте и сам файл проекта;
7. Закрыть – закрыть текущую схему;
8. Закрыть проект – закрыть все схемы проекта и сам проект;
9. Выход – выход из приложения.
(Примечание: схемы проекта и файл проекта должны сохраняться в одной папке).
Пункты меню «Правка»:
1. Отменить – отмена последнего действия;
2. Повторить – повтор отмененного действия;
3. Вырезать – вырезать выделенные объекты из схемы;
4. Копировать – копировать выделенные объекты на схеме;
5. Вставить – вставить скопированные объекты в текущую схему.
6. Сохранить в библиотеку – сохранить измененные параметры блока в библиотеку;
7. Удалить – удалить выделенные объекты из схемы;
8. Выделить все – выделить все объекты на текущей схеме.
Пункты меню «Моделирование»:
1. Запустить – запуск моделирования модели текущего проекта;
2. Остановить – остановка процесса моделирования;
3. Параметры – вызов формы параметров моделирования.
Пункты меню «Настройки»:
1. Администратор – вход в режим администратора (см. приложение 3)
Редактор модели
Редактор модели предназначен для создания непосредственно структурной схемы модели (рис. 4). Каждому редактору соответствует своя схема, проект может содержать от 1-ой до нескольких схем.
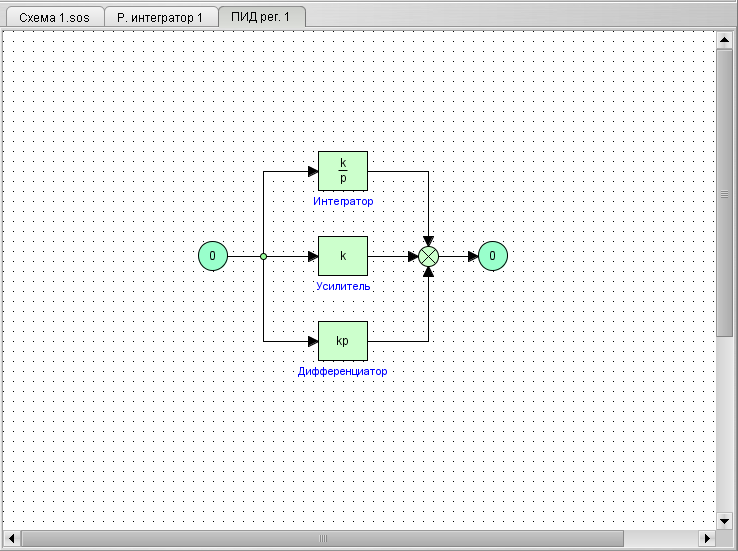
Рис. 4. Редактор моделей
Работа с объектами в редакторе построена по принципу выделения активного объекта. Выделенный объект помечается квадратиками в его углах (рис. 5)
Рис. 5. Выделение объектов
Редактор поддерживает множественное выделение объектов. Для выделения нескольких объектов используется:
· Нажатия ЛКМ на объекте при зажатой клавише Ctrl.
· Выделение областью (нажатие ЛКМ в редакторе и протягивание мыши для образования области).
Все операции (перемещение, копировании, удаления) производятся над всеми выделенными объектами.
Для перемещения объекта используется технология Drag&Drop.
Создание связей между объектами. Все связи в системе имеют прямоугольную конфигурацию. Для проведения связи существует 2 способа:
1) Подвести мышь к концу выходного контакта блока. Курсор поменяет свой вид (рука). Затем щелкнуть ЛКМ и перемещать курсор к требуемому входу блока. Связь будет динамически менять свою конфигурацию. Затем подвести указатель к концу входного блока и опять нажать ЛКМ. По ходу построения связи можно создавать промежуточные точки нажимая ЛКМ в нужных местах редактора. Для отмены еще не законченной связи нажмите Esc.
2) Зажмите клавишу Ctrl и щелкните ЛКМ по блоку источнику, затем, не отпуская Ctrl, щелкните по блоку приемнику. Связь будет проведена автоматически между свободными контактами блоков в соответствии с их порядковыми номерами.
После проведения связи ее модификацию можно изменить 2-мя способами (Drag&Drop):
· Перетаскивать узловые точки связи;
· Перетаскивать линии в составе связи.
Заметим, что при перемещении объекта связь изменяет свою конфигурацию автоматически.
Создание структурных схем. При создании структурных схем можно столкнуться со следующими трудностями:
1) Разветвления сигнала. Его можно произвести двумя способами:
· С помощью ТЭС библиотеки «Разветвитель» (  ), находящимся в разделе «Динамические».
), находящимся в разделе «Динамические».
· Подвести указатель мыши к связи, которую нужно разбить, при нажатой клавише Ctrl. При этом указатель изменит свой изображение на круг в виде разветвителя. Нажмите ЛКМ и разветвитель будет встроен в выбранную связь. Для быстрого изменения направления добавочного контакта произведите двойной щелчок по разветвителю при нажатой клавише Ctrl.
2) Для поворота контактов блока по часовой стрелке нажмите Ctrl+R.
3) Для передачи сигналов из одной схемы в другие используются блоки «Входной сигнал» и «Выходной сигнал» раздела «Субструктуры». Соответствие между сигналами определяется их идентификаторами.
Окно проектов
Менеджер проектов (рис. 6) отображает открытые на данный момент в системе проекты в виде дерева.
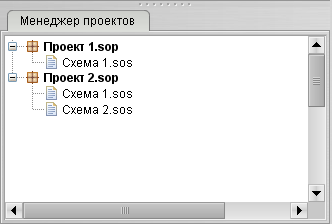
Рис. 6. Менеджер проектов
Контекстное меню проекта (ПКМ по проекту) позволяет закрыть выбранный проект. Контекстное меню схемы позволяет закрыть схему или удалить схему из проекта.
Щелчок ЛКМ по схеме приводит к ее активизации. Если выбранная схема скрыта вкладками с другими схемами, то она будет выдвинута на передний план.
Консоль
Консоль (рис. 7) предназначена для вывода служебных сообщений пользователю. Сюда относится:
· Информация о удачной или неудачной компиляции модели проекта;
· Информация о начале прогона модели и параметрах моделирования;
· Информация о завершении или вынужденном останове процесса моделирования, время за которое было проведено моделирование.
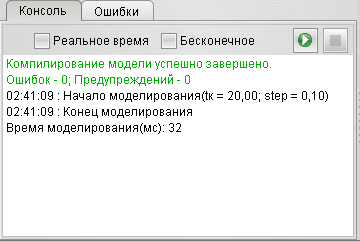
Рис. 7. Консоль
Консоль также содержит кнопки быстрого запуска и остановки моделирования и группу управляющих флажков:
· Реальное время – моделирование будет происходить в реальном времени;
· Бесконечное – устанавливается для отмены ограничений на время моделирования. Моделирование не закончится, пока пользователь не нажмет кнопку «Стоп».
Окно ошибок
Окно ошибок (рис. 8) предназначена для вывода ошибок и предупреждений, связанных с составом структурной схемы (невозможность сформировать поток выполнения команд, неподключенность контактов блоков и т.п.).
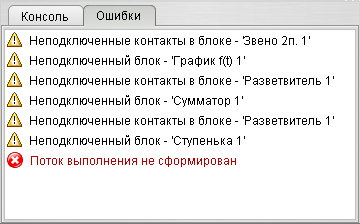
Рис. 8. Окно ошибок
Окно свойств объектов
Менеджер свойств (рис. 9) отображает и позволяет изменять свойства объектов модели. Все свойства объекта поделены на 3 группы:
· Вид – свойства внешнего вида объекта;
· Контакты – положение и вид контактов блока, для некоторых блоков есть возможность добавлять или удалять контакты.
· Параметры – содержит математические параметры объекта, если они существуют (например, коэффициент усиление и т.п.).
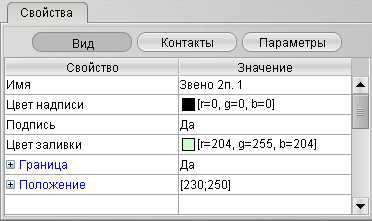
Рис. 9. Свойства объекта, вкладка «Вид»
Изменение свойств объектов интуитивно понятно и построено на использовании диалоговых окон, выпадающих списков, полей ввода. Завершением ввода является нажатие клавиши Enter или снятие фокуса с редактируемого свойства.
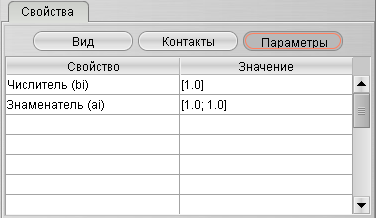
Рис. 9. Свойства объекта, вкладка «Параметры»
На рис. 9 отображены параметры передаточной функции общего вида. Заметим, что оформление векторов значений идет в квадратных скобках через точку с запятой.
Создание ГЭС
Все ГЭС в системе выделяются в рамочку (Рис. 10).
Рис. 10. ГЭС
Для создания ГЭС в окно редактора добавляется типовой объект «ГЭС» раздела библиотеки «Субструктуры». Для того, чтобы редактировать внутреннюю структуру блока необходимо произвести двойной щелчок ЛКМ по ГЭС – появится окно редактора. При построении схемы ГЭС используются все те же, что и при построении обычных моделей. Для добавления входных и выходных контактов в ГЭС используются блоки «Входной порт» и «Выходной порт» соответственно.
Следующим этапом является определение внешних свойств ГЭС. Для этого вызывается контекстное меню блока, пункт «Параметры». На экран появится форма настройки параметров для ГЭС (Рис. 11)
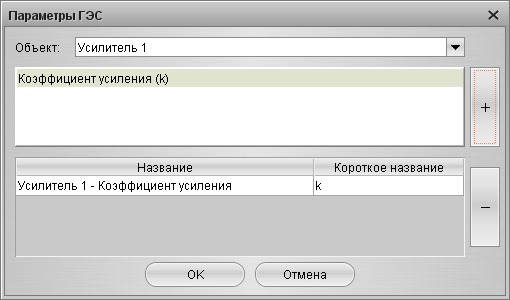
Рис. 11 Форма определения параметров ГЭС
После установки параметров ГЭС они будут отображаться в редакторе свойств ГЭС и могут быть использованы при оптимизации.
Затем пользователь может загрузить созданный ГЭС в библиотеку (контекстное меню ГЭС, пункт «Загрузить в библиотеку).
Моделирование
После создания структурной схемы модели можно проводить моделирование. Для этого вначале задаются параметры моделирования (рис. 12) (меню «Моделирование», пункт «Параметры»)
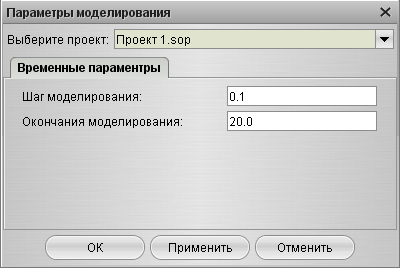
Рис. 12. Настройка параметров моделирования
Затем можно запускать моделирование. Просмотр результатов моделирования (при использовании объектов «Временной график», График y(x)») осуществляется двойным щелчком ЛКМ по соответствующему блоку.
Заметим, что просмотр графиков можно производить непосредственно в процессе моделирования. Для этого вызовите окно графика до моделирования и вытащите график на рабочее пространство. Затем установите графику свойство «Рисовать on-line» и задайте реальное время моделирования (Рис. 13).
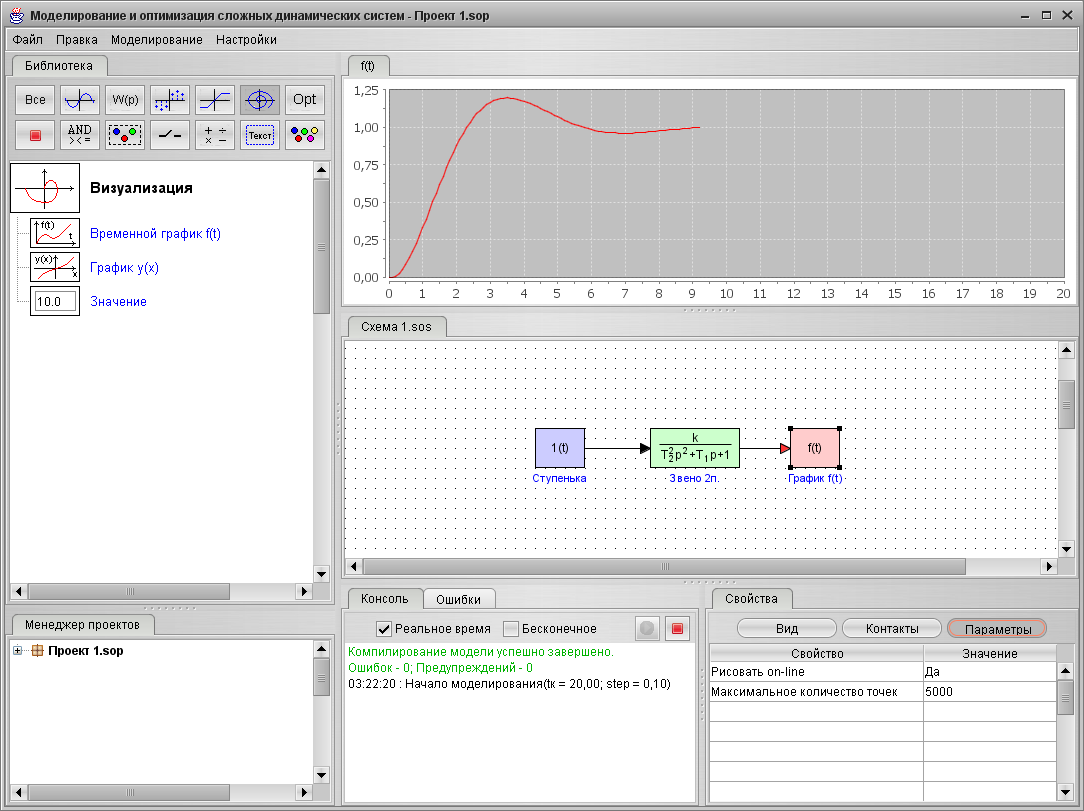
Рис. 13. Просмотр результатов моделирования on-line
Оптимизация
Для организации оптимизации используется блок «Оптимизатор» раздела «Оптимизация» (см. прил. 2)
На рис. 16 изображена схема использования оптимизатора при оптимизации САР по времени регулирования.

Рис. 16 Схема оптимизации САР
Для выбора оптимизируемых параметров используется параметр блока «Оптимизатор» - «Параметры…». Остальные настройки оптимизации также проводятся в параметрах данного блока.
Клавиши быстрого доступа
| Комбинация | Описание |
| Сtrl+O | Открыть проект |
| Ctrl+S | Сохранить |
| Alt+X | Выход |
| Ctrl+Z | Отменить |
| Ctrl+Y | Повторить |
| Ctrl+C | Копировать |
| Ctrl+V | Вставить |
| Ctrl+X | Вырезать |
| Ctrl+F | Копировать в библиотеку |
| Ctrl+A | Выделить все |
| Del | Удалить |
| F9 | Запуск моделирования |
| F8 | Остановка моделирования |
| Ctrl+M | Параметры моделирования |
| Ctrl+R | Поворот контактов блока |
Приложение 2. Библиотека блоков
Библиотека блоков системы имеет следующие разделы:
1) Генераторы;
2) Динамические;
3) Дискретные;
4) Нелинейные;
5) Визуализация;
6) Оптимизация;
7) Управление;
8) Логические;
9) Субструктуры;
10) Ключи;
11) Операции;
12) Оформление;
13) Пользовательские.
Обозначения: СДВ – скалярная действительная величина,
ВДВ – векторная действительная величина,
СЦВ – скалярная целая величина.
Генераторы
Данный раздел содержит блоки, производящие генерацию сигнала различной формы. Данные блоки не имеют входного сигнала.
Модельное время
| Вид в библиотеке | Вид в редакторе |

| 
|
Блок генерирует значение равное текущему времени моделирования:
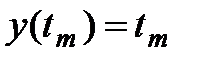 ,
,
где 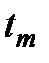 - время моделирования.
- время моделирования.
Параметры:
Блок не имеет параметров.
Ступенька
| Вид в библиотеке | Вид в редакторе |
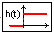
| 
|
Блок генерирует значение по закону:
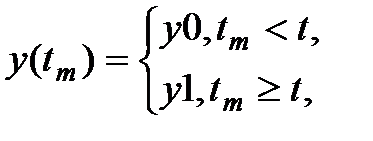
Параметры:
1. Начальный уровень сигнала (у0);
2. –Конечный уровень сигнала (y1) – СДВ;
3. Время скачка (t) – CДВ ( 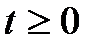 ).
).
Синусоида
| Вид в библиотеке | Вид в редакторе |
| 
|
Блок генерирует синусоидальный сигнал:
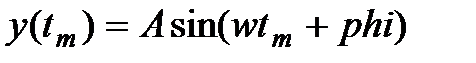
Параметры:
1. Амплитуда сигнал (А) – СДВ;
2. Частота сигнала (w) – СДВ (рад/с);
3. Фазовый сдвиг (phi) – CДВ ( 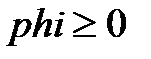 ).
).
Константа
| Вид в библиотеке | Вид в редакторе |
| 
|
Блок генерирует постоянный сигнал:
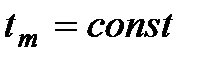
Параметры:
1. Значение (const) – СДВ;
Прямоугольный сигнал
| Вид в библиотеке | Вид в редакторе |
| 
|
Блок генерирует прямоугольный сигнал:
Параметры:
1. Низкий уровень сигнала (y0) – СДВ;
2. Высокий уровень сигнала (y1) – СДВ;
3. Период (Т) – СДВ ( 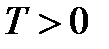 );
);
4. Длительность сигнала (t) – СД ( 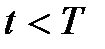 );
);
5. Задержка (phi) – CДВ ( 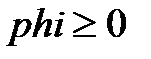 ).
).
Пилообразный сигнал
| Вид в библиотеке | Вид в редакторе |

| 
|
Блок генерирует пилообразный сигнал:
Параметры:
1. Режим пилы – прямая пила, обратная пила;
2. Низкий уровень сигнала (y0) – СДВ;
3. Высокий уровень сигнала (y1) – СДВ;
4. Период (Т) – СДВ ( 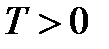 );
);
5. Задержка (phi) – CДВ ( 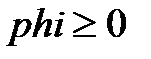 ).
).
Пилообразный сигнал
| Вид в библиотеке | Вид в редакторе |

| 
|
Блок генерирует экспоненциальный сигнал:
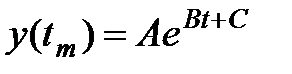 .
.
Параметры:
1. Усиление (А) – СДВ;
2. Коэффициент по времени (В) – СДВ;
3. Сдвиг по времени (С) – СДВ;
Полином
| Вид в библиотеке | Вид в редакторе |

| 
|
Блок генерирует полиномиальный сигнал:
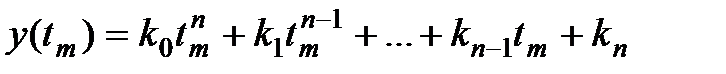 .
.
Параметры:
1. Коэффициенты (ki) - ВДВ.
Кусочная функция
| Вид в библиотеке | Вид в редакторе |
| 
|
Блок генерирует кусочно-линейную величину.
Параметры:
1. Режим – кусочно-постоянная, кусочно-линейная;
2. Времена переходов (ti) – ВДВ, возрастающая последовательность;
3. Значения функций (vi) – ВДВ;
Динамические
Данный раздел содержит в своей основе блоки-преобразователи сигнала, используемые при построении моделей САР.
Сумматор
| Вид в библиотеке | Вид в редакторе |
| 
|
Блок суммирует входные сигналы с весовыми коэффициентами.
Параметры:
1. Коэффициенты (k) – ВДВ;
Максимальное число входов – 3, минимальное число входов – 2.
Передаточная функция
| Вид в библиотеке | Вид в редакторе |

| 
|
Блок реализует передаточную функцию общего вида.
Параметры:
1. Числитель (bi) – ВДВ;
2. Знаменатель (ai) – ВДВ;
Усилитель
| Вид в библиотеке | Вид в редакторе |

| 
|
Блок реализует безынерционное звено.
Параметры:
1. Коэффициент усиления (k) – CДВ ( 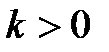 );
);
Интегратор
| Вид в библиотеке | Вид в редакторе |
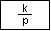
| 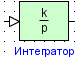
|
Блок реализует идеальное интегрирующее звено.
Параметры:
1. Коэффициент усиления (k) – CДВ ( 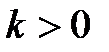 ).
).
Интегратор
| Вид в библиотеке | Вид в редакторе |
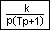
| 
|
Блок является реальным интегрирующим звеном, реализован в виде субмодели (последовательное соединение интегратора и звена 1-ого порядка)
Параметры:
1. Коэффициент усиления (k) – CДВ ( 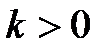 );
);
2. Постоянная времени (T) – CДВ ( 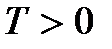 ).
).
Дифференциатор
| Вид в библиотеке | Вид в редакторе |

| 
|
Блок реализует дифференцирующее звено.
Параметры:
1. Коэффициент усиления (k) – CДВ ( 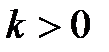 );
);
Реальный дифференциатор
| Вид в библиотеке | Вид в редакторе |
| 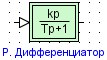
|
Блок является реально-дифференцирующим звеном, реализован в виде субмодели (последовательное соединение дифференциатора и звена 1-ого порядка)
Параметры:
1. Коэффициент усиления (k) – CДВ ( 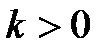 );
);
2. Постоянная времени (T) – CДВ ( 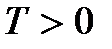 ).
).
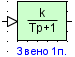
Звено 1-ого порядка
| Вид в библиотеке | Вид в редакторе |
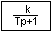
| 
|
Блок реализует инерционное звено 1-ого порядка.
Параметры:
1. Коэффициент усиления (k) – CДВ ( 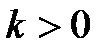 );
);
2. Постоянная времени (T) – CДВ ( 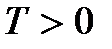 ).
).
Звено 2-ого порядка
| Вид в библиотеке | Вид в редакторе |
| 
|
Блок реализует звено 2-ого порядка (колебательное или инерционное).
Параметры:
1. Коэффициент усиления (k) – CДВ ( 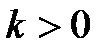 );
);
2. Постоянная времени ( 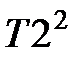 ) – CДВ (
) – CДВ ( 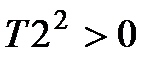 );
);
3. Постоянная времени (  ) – CДВ (
) – CДВ (  ).
).
Звено 2-ого порядка
| Вид в библиотеке | Вид в редакторе |
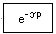
| 
|
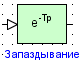
Блок реализует звено чистого запаздывания.
Параметры:
1. Время запаздывания (tau) – CДВ ( 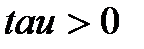 );
);
Звено 2-ого порядка
| Вид в библиотеке | Вид в редакторе |
| 
|
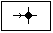
Блок производит разветвление сигнала без изменений.
Параметры:
Блок не имеет параметров.
Максимальное число выходов – 3, минимальное число выходов – 2.
Звено 2-ого порядка
| Вид в библиотеке | Вид в редакторе |

| 
|
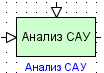
Блок реализует функции аналитического анализа САР (корневой и частотный анализ).
Вход слева – вход САР.
Вход сверху – выход САР
Выход – переходная характеристика САР.
Параметры:
Блок не имеет параметров.
ПИ регулятор
| Вид в библиотеке | Вид в редакторе |
| 
|
Блок является пропорционально-интегральным регулятором, реализован в виде субмодели (параллельное соединение усилителя и интегратора).
Параметры:
1. Коэффициент усиления (П) – CДВ ( 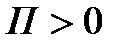 );
);
2. Коэффициент усиления (И) – CДВ ( 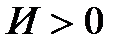 ).
).
ПД регулятор
| Вид в библиотеке | Вид в редакторе |

| 
|
Блок является пропорционально-дифференциальным регулятором, реализован в виде субмодели (параллельное соединение усилителя и дифференциатора).
Параметры:
1. Коэффициент усиления (П) – CДВ ( 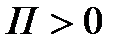 );
);
2. Коэффициент усиления (Д) – CДВ ( 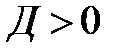 ).
).
ПИД регулятор
| Вид в библиотеке | Вид в редакторе |
| 
|
Блок является пропорционально-интегрально-дифференциальным регулятором, реализован в виде субмодели (параллельное соединение усилителя и дифференциатора и интегратора).
Параметры:
1. Коэффициент усиления (П) – CДВ ( 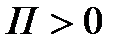 );
);
2. Коэффициент усиления (И) – CДВ ( 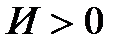 ).
).
3. Коэффициент усиления (Д) – CДВ ( 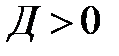 ).
).
Дискретные
Экстраполято 0-ого порядка
| Вид в библиотеке | Вид в редакторе |
| 
|
Блок реализует экстраполяцию нулевого порядка:
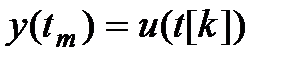 ,
,
где 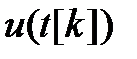 - значение входного сигнала в последний момент дискретизации
- значение входного сигнала в последний момент дискретизации 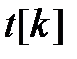 .
.
Параметры:
1. Период квантования (T) – CДВ ( 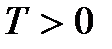 ).
).
Экстраполято 1-ого порядка
| Вид в библиотеке | Вид в редакторе |
| 
|
Блок реализует экстраполяцию первого порядка:
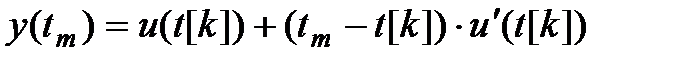 ,
,
где 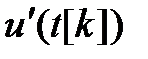 - значение производной входного сигнала в последний момент дискретизации
- значение производной входного сигнала в последний момент дискретизации 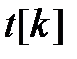 .
.
Параметры:
1. Период квантования (T) – CДВ ( 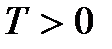 ).
).
Нелинейные
Раздел содержит нелинейный блоки.
Ограничитель
| Вид в библиотеке | Вид в редакторе |
| 
|
Блок реализует преобразование входного сигнала посредством единой нелинейной статической характеристики типа "насыщение" по следующему алгоритму:
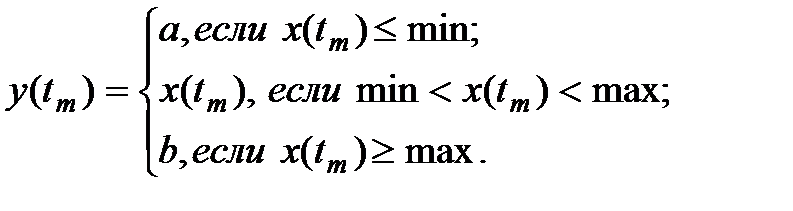
Параметры:
1. Нижняя граница насыщения (min) – CДВ.
2. Верхняя граница насыщение (mаx) – CДВ ( 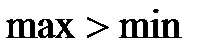 ).
).
Ограничитель
| Вид в библиотеке | Вид в редакторе |
| 
|
Блок реализует преобразование входного сигнала посредством единой нелинейной статической характеристики типа "линейная с зоной нечувствительности" по следующему алгоритму:
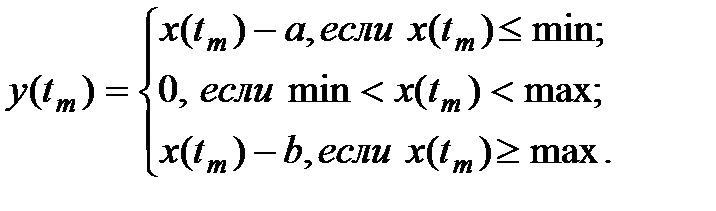
Параметры:
1. Нижняя граница нечувствительности (min) – CДВ;
2. Верхняя граница нечувствительности (mаx) – CДВ ( 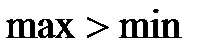 ).
).
Реле
| Вид в библиотеке | Вид в редакторе |
| 
|
Блок реализует преобразование входного сигнала посредством единой нелинейной статической характеристики типа "релейная неоднозначная" при различных начальных условиях по следующему алгоритму:
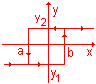
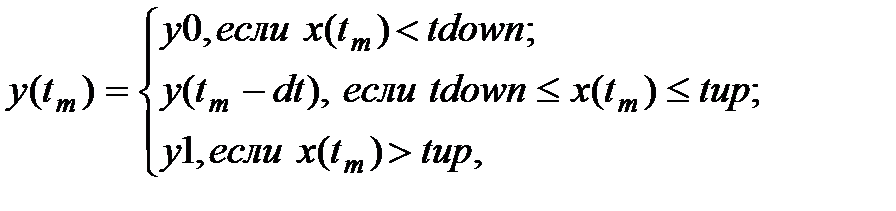
где dt - предыдущий временной шаг интегрирования.
Параметры:
1. Низкий уровень сигнала (y0) – CДВ;
2. Высокий уровень сигнала (y1) – CДВ;
3. Точка выключения (tdown) – СДВ;
4. Точка включения (tup) – СДВ( 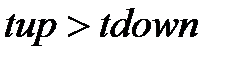 ).
).
Квантователь по уровню
| Вид в библиотеке | Вид в редакторе |
| 
|
Блок реализует квантование по уровню.
Параметры:
1. Шаг квантования (level) – CДВ( 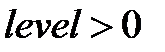 ).
).
Ограничитель по производной
| Вид в библиотеке | Вид в редакторе |
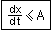
| 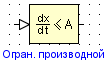
|
Блок реализует ограничение входного сигнала по производной.
Параметры:
1. Минимальное значение производной (min) – CДВ;
2. Максимальное значение производной (max) – CДВ( 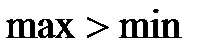 ).
).
Ограничитель по производной
| Вид в библиотеке | Вид в редакторе |

| 
|
Блок реализует счетчик.
Вход u – увеличение выходного сигнала;
Вход d – уменьшение выходного сигнала.
Параметры:
1. Режим работы – по переднему фронту, по заднему фронту;
2. Точность (знаков) – точность, до которой округляется входное значение.
Визуализация
Временной график f(t)
| Вид в библиотеке | Вид в редакторе |
| 
|
Блок реализует построение графика от времени моделирования. Показ графика – двойной щелчок ЛКМ по блоку.
Параметры:
1. Рисовать on-line – да/нет – добавление точек на график динамически в процессе моделирования.
2. Максимальное количество точек – максимальное кол-во точек отображаемое графиком.
Максимальное количество входов – 8.
График y ( x )
| Вид в библиотеке | Вид в редакторе |
| 
|
Блок реализует построение графика y(x). Показ графика – двойной щелчок ЛКМ по блоку.
Параметры:
1. Рисовать on-line – да/нет – добавление точек на график динамически в процессе моделирования.
2. Максимальное количество точек – максимальное кол-во точек отображаемое графиком.
Максимальное количество входов – 4 пары.
Временной график f(t)
| Вид в библиотеке | Вид в редакторе |

| 
|
Блок реализует вывод значения скалярного сигнала.
Параметры:
1. Количество знаков – кол-во отображаемых знаков после запятой.
2. Рисовать on-line – да/нет – добавление точек на график динамически в процессе моделирования.
Оптимизация
Оптимизатор
| Вид в библиотеке | Вид в редакторе |
| 
|
Блок реализует параметрическую оптимизации системы.
Параметры:
1. Включен – Включен/Выключен – проведение оптимизации;
2. Параметры – выбор оптимизируемых параметров;
3. Тип поиска – Минимум/максимум;
4. Максимальное число прогонов за цикл – максимальное цисло прогонов модели за цикл;
5. Количество циклов – СЦВ - кол-во попыток с разными начальными точками;
6. Разброс начальных точек – СДВ – разброс начальных точек при случайном распределении начальных точек;
7. Восстанавливать параметры – да/нет - восстанавливать значения оптимизируемых параметров после окончания оптимизации
8. Метод – выбор метода (Хука-Дживса, Нелдера-Мида).
Перерегулирование
| Вид в библиотеке | Вид в редакторе |
| 
|
Блок реализует расчет перерегулирования сигнала. Подключается к выходу САР.
Параметры:
Блок не имеет параметров.
Время регулирования
| Вид в библиотеке | Вид в редакторе |
| 
|
Блок реализует расчет время регулирования процесса. Подключается к выходу САР.
Параметры:
1. Максимальное отклонение (%) – СДВ.
Управление
Остановить
| Вид в библиотеке | Вид в редакторе |

| 
|
Блок производит остановку процесса моделирования при подаче значения входа, превышающего порогового значения.
Параметры:
1. Значение остановки (stopV) – СДВ.
Остановить по сходимости
| Вид в библиотеке | Вид в редакторе |

| 
|
Блок производит остановку процесс моделирования по сходимости процесса в САР. Если процесс не сходится моделирования останавливается во время limitT
Параметры:
1. Предельное время (limitT) – СДВ.
Время моделирования
| Вид в библиотеке | Вид в редакторе |

| 
|
Блок производит установку времени окончания моделирования с входного сигнала.
Параметры:
Блок не имеет параметров.
Логические
Сравнение
| Вид в библиотеке | Вид в редакторе |
| 
|
Блок производит сравнение двух входных сигналов. На выход подается 1.0 (Истина) или 0.0 (Ложь).
Параметры:
1. Тип операции – больше, меньше, равно, не равно, больше или равно, меньше или равно;
2. Точность (знаков) – точность, до которой округляются входные значения.
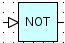
Сравнение
| Вид в библиотеке | Вид в редакторе |

| 
|
Блок производит операцию логического отрицания по формуле: 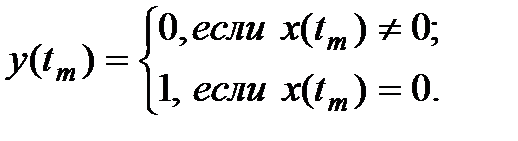
Параметры:
1. Точность (знаков) – точность, до которой округляется входное значение.
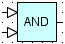
Логическая операция
| Вид в библиотеке | Вид в редакторе |

| 
|
Блок производит логическую операцию.
Параметры:
1. Операция – И, ИЛИ, исключающее ИЛИ.
2. Точность (знаков) – точность, до которой округляется входное значение.
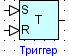
Триггер
| Вид в библиотеке | Вид в редакторе |

| 
|
Блок реализует RS и JK триггер.
Параметры:
1. Тип триггера – RS или JK;
2. Точность (знаков) – точность, до которой округляется входное значение.
Субструктуры
Входной порт/Выходной порт
| Вид в библиотеке | Вид в редакторе |
| 
|
Блок используется для создания входных и выходных портов в субмоделях (ГЭС).
Параметры:
Блок не имеет параметров.
Ключи
Ключ
| Вид в библиотеке | Вид в редакторе |
| 
|
Блок является ключом с одним входом и двумя состояниями: замкнут/разомкнут. При разомкнутом состоянии на выход подается 0. Переключать состояния можно двойным щелчком ЛКМ по блоку.
Параметры:
1. Состояние – Выключен/Включен.
Ключ многовходовый
| Вид в библиотеке | Вид в редакторе |
| 
|
Блок является ключом с несколькими входами. Положение переключателя (указано на блоке) определяет сигнал, подающийся на выход. Переключать состояния можно двойным щелчком ЛКМ по блоку.
Параметры:
1. Состояние – СЦВ – номер входа.
Максимальное количество входов – 8.
Ключ управляемый
| Вид в библиотеке | Вид в редакторе |
| 
|
Блок является ключом с несколькими входами. Положение переключателя (указано на блоке) определяется управляющим сигналом, в соответствии с порогами переключения.
Вход сверху: управляющий сигнал;
Входы слева: информационные сигналы.
Параметры:
1. Пороги переключения – ВДВ;.
Максимальное количество входов – 4.
Операции
Сумматор
| Вид в библиотеке | Вид в редакторе |
| 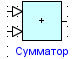
|
Блок производит суммирование входов.
Параметры:
Блок не имеет параметров.
Максимальное число входов – 4.
Сумматор с весами
| Вид в библиотеке | Вид в редакторе |
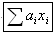
| 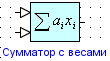
|
Блок производит суммирование сигналов входов с весовыми коэффициентами ki.
Параметры:
1. Коэффициенты (ki) – ВДВ.
Максимальное число входов – 4.
Вычитатель
| Вид в библиотеке | Вид в редакторе |
| 
|
Блок производит вычитание сигналов.
Параметры:
Блок не имеет параметров.
Умножитель
| Вид в библиотеке | Вид в редакторе |
| 
|
Блок производит перемножение сигналов.
Параметры:
Блок не имеет параметров.
Максимальное число входов – 4.
Делитель
| Вид в библиотеке | Вид в редакторе |
| 
|
Блок производит деление сигналов.
Параметры:
Блок не имеет параметров.
Модуль
| Вид в библиотеке | Вид в редакторе |

| 
|
Блок возвращает модуль исходного сигнала.
Параметры:
Блок не имеет параметров.
Модуль
| Вид в библиотеке | Вид в редакторе |

| 
|
Блок возвращает знак исходного сигнала.
Параметры:
Блок не имеет параметров.
Оформление
Надпись
| Вид в библиотеке | Вид в редакторе |

| 
|
Блок оформления схемы: надпись.
Параметры:
Блок не имеет параметров.
Граница
| Вид в библиотеке | Вид в редакторе |
| 
|
Блок оформления схемы: граница.
Параметры:
Блок не имеет параметров.
Пользовательские
Раздел является пустым и предназначен для добавления составных блоков пользователями.
Приложение 3. Руководство администратора
Вход в режим администратора
Режим администратора позволяет пользователю получить ряд дополнительных функций по работе с библиотекой блоков.
Для того чтобы войти в режим администратора необходимо: выбрать в главном меню раздел «Настройки», пункт «Администратор…». Далее появится окно режима администратора (рис. 1).
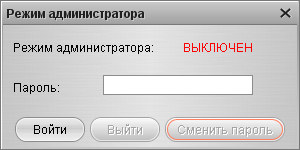
Рис. 1 Окно режима администратора
Верхняя надпись сигнализирует о текущем состоянии режима: ВКЛЮЧЕН/ВЫКЛЮЧЕН.
Для входа под администратором необходимо набрать пароль и нажать кнопку «Войти». Если пароль верен, окно просигнализирует, что режим администратора включен (рис. 2).
Рис. 2 Режим администратора включен
Администратор может в любое время выйти из режима, а также сменить пароль.
Приложение 4. Руководство по установке
Установка программы
Программа распространяется одним архивом. Для установки необходимо распаковать архив в выбранное место на жестком диске. Программа также может работать и со сменных носителей.
Основные компоненты распакованного приложения:
1) Папка «libobjects» - объекты библиотеки элементов;
2) Папка «pics» - рисунки, используемые в приложении;
3) Папка «prg» - папка, где сохраняются модели (по умолчанию);
4) Папка «temp» - папка временного хранения;
5) Файл «codec.dck» – файл настроек конфигурации рабочего окна;
6) Файл «configlib.dtd» - файл ограничений для файла «library.xml»;
7) Файл «library.xml» - файл, содержащий структуру библиотеки ТЭС;
8) Файл «settings.bin» - файл общих настроек приложения;
9) Файл «SimOpt.jar» - исполняемый java-архив;
10) Файл «run.bat» - пакетный файл запуска файла «SimOpt.jar».
Запуск приложения
Для запуска приложения необходимо запустить на исполнение файл «run.bat».
Список литературы
1. Марголис Б.И. Компьютерные методы анализа и синтеза систем автоматического регулирования – 1-е издание. – Тверь: ТГТУ, 2006. – 100с.
2. Советов Б. Я., Яковлев С. А., Моделирование систем: Учеб. для вузов — 3-е изд., перераб. и доп. — М.: Высш. шк., 2001. — 343 с.
3. Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся втузов. – М.: Наука, 1986. – 544 с.
4. Банди Б. Методы оптимизации. Вводный курс: Пер. С англ. – М.: Радио и связь, 1988. – 128 с.: ил.
5. Хорстманн К., Корнелл Г. Java 2. Библиотека профессионала, том 1, 2, 7-е изд.: Пер. с англ. – М.: Издательский дом «Вильямс», 2008. – 896 с. : ил.
6. Козлов О.С. и др. Программный комплекс «Моделирование в технических устройствах» (ПК «МВТУ») - http://model.exponenta.ru/mvtu/20050615.html.
7. Клиначев Н.В. О явном и неявном решателях программ математического моделирования динамических систем - http://model.exponenta.ru/impl_slv.html.
8. Ю. Б. Колесов, Ю. Б. Сениченков. Моделирование систем. Динамические и гибридные системы. – Сп.б.: БХВ, 2006. – 224 с.
9. Клиначев Н.В. Обзор архитектурного построения программ математического моделирования динамических систем. - http://model.exponenta.ru/simkernel.html.
10. Клиначев Н.В. Преодоление барьеров или критерии оценки программ для симуляции движения (моделирования) систем - http://model.exponenta.ru/sim_prog.html
11. [D.Harel, Statecharts: A Visual Formalism for Complex Systems. Science of Computer Programming, North-Holland, Vol.8, No.3, 1987, pp. 231-274.]
12. UML [Booch G., Jacobson I. and Rumbaugh J.: "The Unified Modeling Language for Object-Oriented Development", Documentation Set Version 1.1, September 1997].
C истема моделирования и оптимизации
Сложных динамических систем
УЧЕБНОЕ ПОСОБИЕ
Григорьев В.А.
Марголис Д. Б.
Тверь 2012
Оглавление
Введение. 6
1 Обзор систем моделирования динамических систем. 9
1.1 Математическое моделирование. 9
1.2 Понятие простой динамической системы.. 10
1.3 Сложная динамическая система. 11
1.3.1 Структурно-сложная динамическая система. 11
1.3.2 Поведенческая сложность динамической системы.. 15
1.3.3 Структурно-сложная гибридная система. 16
1.4 Имитационное моделирование. 17
1.5 Пакеты визуального моделирования. 18
1.6 Обзор пакетов моделирования. 19
1.7 Система моделирования MatLab. 23
1.8 Система моделирования МВТУ.. 24
2 Математическое и алгоритмическое обеспечение системы моделирования динамических систем. 27
2.1 Математическое описание простой непрерывной динамической системы 27
2.2 Идентификация динамической системы.. 31
2.2.1 Представление динамической системы в системе моделирования 31
2.2.2 Определение внутренних координат системы.. 33
2.2.3 Формирование структурной матрицы системы.. 34
2.3 Получение переходного процесса аналитическим способом. 35
2.3.1 Расчет общей передаточной функции системы.. 35
2.3.2 Переход к полиномиальной форме представления передаточной функции 38
2.3.3 Получение аналитической функции переходного процесса. 39
2.4 Моделирование непрерывных динамических систем. 44
2.4.1 Численные методы решения дифференциальных уравнений. 45
2.4.2 Решатели моделирующих программ. 46
2.4.3 Методы дифференцирования. 47
2.4.4 Модель передаточной функции общего вида. 47
2.4.5 Модель звена запаздывания. 48
2.5 Моделирование дискретных динамических систем. 48
2.5.1 Моделирование дискретных событий. 48
2.5.2 Модель экстраполятора 0-го порядка. 49
2.6 Оптимизация. 49
2.6.1 Методы безусловной оптимизации. 51
2.6.2 Метод Хука-Дживса. 54
2.6.3 Метод Нелдера-Мида. 56
2.6.4 Условная оптимизация. 58
2.6.5 Нахождение глобального минимума целевой функции. 60
3 Разработка системы моделирования сложных динамических систем. 64
3.1 Требования к функциям системы.. 64
3.2 Требования к характеристикам системы.. 65
3.3 Требования к архитектуре системы.. 67
3.4 Выбор средств реализации системы.. 68
3.5 Объектно-ориентированное моделирование. 69
3.6 Проектирование системы на языке UML. 70
3.6.1 Диаграмма вариантов использования. 70
3.6.2 Диаграмма классов. 71
3.6.3 Диаграмма состояний. 74
3.6.4 Диаграмма реализации. 74
3.7 Архитектура и функциональные возможности системы.. 75
3.7.1 Рабочее пространство системы.. 76
3.7.2 Графический редактор моделей системы.. 78
3.7.3 Подсистема представления результатов. 79
3.7.4 Библиотека типовых блоков. 80
3.7.5 Математическое ядро. 81
3.7.6 Система помощи. 83
3.8 Сравнение с ПК «МВТУ». 84
4 Тестирование разработанной системы моделирования. 86
4.1 Имитационное моделирование линейной непрерывной САР. 86
4.2 Оптимизация линейной непрерывной САР. 88
4.3 Анализ линейной непрерывной САР. 90
Заключение. 95
Приложение 1. Руководство пользователя. 97
Приложение 2. Библиотека блоков. 114
Приложение 3. Руководство администратора. 142
Приложение 4. Руководство по установке. 146
Список литературы.. 147
Введение
Имитационное моделирование на цифровых вычислительных машинах является одним из наиболее мощных средств исследования, в частности, сложных динамических систем. Как и любое компьютерное моделирование, оно дает возможность проводить вычислительные эксперименты с еще только проектируемыми системами и изучать системы, натурные эксперименты с которыми, из-за соображений безопасности или дороговизны, не целесообразны. В тоже время, благодаря своей близости по форме к физическому моделированию, это метод исследования доступен более широкому кругу пользователей.
В настоящее время, когда компьютерная промышленность, предлагает разнообразнейшие средства моделирования, любой квалифицированный инженер, технолог или менеджер должен уметь уже не просто моделировать сложные объекты, а моделировать их с помощью современных технологий, реализованных в форме графических сред или пакетов визуального моделирования.
На данный момент тема имитационного моделирования является достаточно изученной, существует много пакетов имитационного моделирования промышленного качества. Существует большое количество литературы, освещающей вопросы применения данных пакетов. Тем не менее, применение конкретных численных методов при реализации систем моделирования, описано не достаточно, что затрудняет разработку аналогов таких систем.
Не все существующие системы моделирования в полной мере отвечают требованиям, связанным с использованием данных систем в процессе высшего обучения в технических ВУЗах. Отрицательные черты данных пакетов с точки зрения использования их в образовательном процессе обусловлены в первую очередь их коммерческой направленностью. Зачастую избыточность функциональных возможностей данных систем моделирования приводит к сложности и трудоемкости их изучения. Также минусом является закрытость математических ядер и невозможность их изучения и модернизации. Еще одним препятствием для изучения может быть отсутствие грамотной локализации самой программы и документации к ней.
Таким образом, представляется актуальным создание свободно распространяемой некоммерческой системы моделирования с открытым исходным кодом, которая бы учитывала специфику использования в образовательном процессе.
Целью работы является разработка программного обеспечения для проведения визуального моделирования, анализа и оптимизации сложных динамических систем.
Для достижения данной цели необходимо решить следующие задачи:
1) провести анализ существующих систем моделирования;
2) формирование требований к инструментарию;
3) разработка алгоритмического обеспечения;
4) разработка архитектуры программного обеспечения;
5) реализация программного обеспечения;
6) исследование разработанного программного обеспечения.
Объектом исследования в данной работе является моделирование динамических систем.
Предметом исследования является методы разработки программного обеспечения для визуального моделирования и оптимизации динамических систем.
Практическая ценность работы заключается в разработке алгоритмического и программного обеспечения для системы моделирования и оптимизации сложных динамических систем.
Разработанная система направлена на обучение студентов по дисциплинам «Основы теории управления», «Моделирование» на кафедре ЭВМ ТГТУ. Она была апробирована на кафедре ЭВМ ТГТУ.
В первой главе работы дается понятие простой и сложной динамической системы, понятие имитационного моделирования. Также здесь проводится анализ существующих средств визуального имитационного моделирования, выявляются их достоинства и недостатки.
Во второй главе описывается теоретическая база исследования, рассматриваются методы математической формализации, а также численные методы моделирования и оптимизации сложных динамических систем.
В третьей главе описываются конкретные этапы разработки программного обеспечения, его архитектура, используемые технологии.
В четвертой главе проводится постановка и выполнение вычислительного эксперимента с использованием разработанного инструментария. Описывается порядок проведения эксперимента, проводится непосредственно эксперимент и делается анализ его результатов.
1
Дата: 2019-07-24, просмотров: 409.