Задача №1
Расставьте в клетках квадрата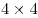 
одну единицу, две двойки, 
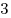тройки, 
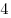четверки, 
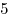пятерок и еще одну любую цифру по своему выбору так, чтобы во всех строках получилась одна и та же сумма цифр.
Решение
| 5 | 4 | 3 | 4 |
| 5 | 4 | 2 | 5 |
| 1 | 3 | 9 | 3 |
| 5 | 5 | 2 | 4 |
.Задача №2
Расположите на плоскости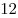 
спичек так, чтобы они образовали как можно больше различных квадратов. Укажите в ответе число этих квадратов.
Решение ____________ — размер спички.
- 25 квадратов
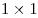; - 16 квадратов
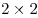; - 9 квадратов
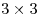; - 4 квадрата ;
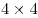- 1 квадрат
.
.
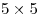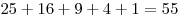Ответ: 55 квадратов.
.Задача №3:
Аня хочет положить в каждую коробку одинаковое число своих игрушек. Сначала она попыталась разложить их по 12 в каждую коробку, но 5 игрушек оказались лишними. Затем она попробовала разложить их по 15 в каждую коробку, но для последней коробки остались только 2 игрушки. Тогда Аня догадалась взять еще одну коробку. Сколько игрушек Аня должна теперь положить в каждую коробку, чтобы добиться своей цели?
Решение Пусть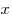 
— количество тугриков у Васи. Тогда, 
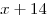— стоимость 39 солдатиков; 
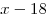— стоимость 35 солдатиков. Значит, 4 солдатика стоят 
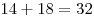тугрика. 1 солдатик стоит 
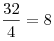тугриков. У Васи было 
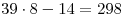тугриков.
Задача №4
Из книги выпал кусок, первая страница которого имеет номер 143, а номер последней состоит из тех же цифр, но записанных в другом порядке. Сколько страниц выпало из книги?
Задача №5
Три яблока, четыре груши и один персик стоят 40 руб. Одно яблоко, четыре груши и персик стоят 32 руб. Сколько стоят одно яблоко, одна груша и один персик, если персик стоит столько, сколько стоят два яблока?
Задача №6
Кенгуру мама прыгает за 1 секунду на 3 метра, а её маленький сынишка прыгает на 1 метр за полсекунды. Они одновременно стартовали от бассейна к эвкалипту по прямой. Сколько секунд мама будет ждать сына под деревом, если расстояние от бассейна до дерева 240 метров? (40 секунд)
Задача №7
Найдите периметр и площадь прямоугольника со сторонами 6 см и 8 см.
Задача №8
Используя переместительное и сочетательное свойства умножения, упростить:
11•х•30
Задача №9
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть:
А) слагаемое
В) вычитаемое
С) число 10
D) известное частное
E) разность
Задача №10
В три банки с надписями «малиновое», «клубничное» и «малиновое или клубничное» налили смородиновое, малиновое и клубничное варенье. Все надписи оказались неправильными. Какое варенье налили в банку «клубничное»?
Задача №11
Коробку размером 30 х 30 х 50 нужно наполнить одинаковыми кубиками.
Какое минимальное количество кубиков позволит это сделать?
A) 15
B) 30
C) 45
D) 75
E) 150
Задача №12
Задания для школьной олимпиады: примеры и выражения. В записи (88888888) нужно поставить знаки сложения таким образом, чтобы получилась сумма, которая будет равна 1000.
Задача №13
В ящике лежат шары: 5 красных, 7 синих и 1 зелёный. Сколько шаров надо вынуть, чтобы достать два шара одного цвета?
Ответы к задачам
Задача 4
172 страницы
Задача 5 груша стоит 5 рублей, яблоко — 4 рубля, персик — 8 рублей
Задача 6
4 руб.
8 руб.
5 руб.
Задача 7
28 см и 48 см²
В пещере старый пират разложил свои сокровища в 3 цветных сундука, стоящих вдоль стены: в один - драгоценные камни, а в другой - золотые монеты, а в третий - оружие. Он помнит, что :
- красный сундук правее, чем драгоценные камни
- оружие правее, чем красный сундук.
В сундуке какого цвета лежит оружие, если зелёный сундук стоит левее, чем синий?
Решение :
ДК - зелёный
ЗC - красный
330x
Задача 8
вариант E
Задача 9
Так как все надписи неправильные, то в третьей банке не может быть ни малиновое, ни клубничное варенье. Значит, там смородиновое варенье. Тогда клубничное и малиновое должны быть в первых двух банках. А так как надписи неправильные, то в банке «клубничное» на самом деле малиновое варенье.
Задача 10
вариант C
Задача 11
Способ 1: 88+8+8+8+888=1000
Способ 2: 8+8+888+88+8=1000
Задача 12
надо вынуть 4 шара
Задача 13:
О - синий
Задача1 4 :
Девять осликов за 3 дня съедают 27 мешков корма.
Сколько корма надо пяти осликам на 5 дней?
Решение :
1 шаг 9 осликов в 1 день - 27 : 3= 9м.
2 шаг 1 ослик в 1 день - 9 : 9 = 1 м.
3 шаг 5 осликов в 1 день - 5 * 1 = 5 м.
4 шаг 5 осликов за 5 дней - 5 * 5 = 25 м.
Задача 15 :
Кенгуру мама прыгает за 1 секунду на 3 метра, а её маленький сынишка прыгает на 1 метр за 0,5 секунды.
Они одновременно стартовали от бассейна к эвкалипту по прямой.
Сколько секунд мама будет ждать сына под деревом, если расстояние от бассейна до дерева 240 метров
Решение :
1 шаг 240 : 3 = 80 (с) скакала мама Кенгуру
2 шаг сын за 0,5 с - 1 м, за 1 с - 2 м
3 шаг 80 * 2 = 160 (м) проскачет кенгурёнок за 80 с
4 шаг 240 - 160 = 80 (м) осталось проскакать кенгурёнку когда
мама уже под эвкалиптом
5 шаг 80 : 2 = 40 (с)
Ответ: 40 секунд.
Задача 16 :
На скотном дворе гуляли гуси и поросята.
Мальчик сосчитал количество голов, их оказалось 30, а затем он сосчитал количество ног, их оказалось 84.
сколько гусей и сколько поросят было на школьном дворе?
Решение :
1 шаг Представьте, что все поросята подняли по две ноги вверх
2 шаг на земле осталось стоять 30 * 2 = 60 ног
3 шаг подняли вверх 84 - 60 = 24 ноги
4 шаг подняли 24 : 2 = 12 поросят
5 шаг 30 - 12 = 18 гусей
Ответ: 12 поросят и 18 гусей.
Задача 17
Инженер ежедневно приезжал на станцию в одно и то же время, и в то же время за ним подъезжала машина, на которой он ехал на завод.
Однажды инженер приехал на станцию на 55 мин раньше обычного.
Сразу пошел навстречу машине и приехал на завод на 10 мин раньше, чем обычно.
Во сколько раз скорость инженера меньше скорости машины?
Решение:
За 10 мин машина проходит путь, равный двойному расстоянию от станции до места встречи инженера с машиной.
Значит, путь от станции до места встречи машина проходит за 5 мин.
На месте встречи машина была за 5 мин до времени обычного приезда инженера на станцию, значит, путь от станции до места встречи инженер шел 55 мин - 5 мин = 50 мин.
Следовательно, скорость инженера в 50 : 5 = 10 раз меньше скорости машины.
Задача 18
В триседьмом царстве живут драконы.
У каждого дракона одна, две или три головы,
а) Может ли у 40 % драконов быть 60 % голов?
б) Может ли у 40 % драконов быть 70 % голов?
Решение:
а) Покажем, что у 40% драконов может быть 60% голов.
Пусть в этом царстве живет 100 драконов: 40 драконов с одной головой, 20 – с двумя головами и 40 – с тремя.
Тогда число голов у всех драконов равно
40 • 1 + 20 • 2 + 40 • 3 = 200.
При этом все 40 трехглавых драконов, что составляет 40% от общего числа драконов, имеют 40 • 3 = 120 голов, что составляет
120/200 • 100% = 60% от общего числа голов.
б) Пусть число драконов равно х, а общее число голов у них равно у.
Предположим, что какие-то 40% драконов имеют 70% голов.
Тогда, поскольку каждый из этих драконов имеет не более трех голов, то 0,7у = 3 • 0,4х.
С другой стороны, поскольку остальные 60% драконов имеют 30% голов и у каждого из них не менее одной головы, то 0,6х = 0,3y.
Но эти неравенства не могут выполняться одновременно, так как они равносильны соответственно 7у = 12х и 12x = 6у.
Поэтому у 40% драконов не может быть 70% голов.
Задача 19
В пещере старый пират разложил свои сокровища в 3 цветных сундука, стоящих вдоль стены: в один - драгоценные камни, а в другой - золотые монеты, а в третий - оружие. Он помнит, что :
- красный сундук правее, чем драгоценные камни
- оружие правее, чем красный сундук.
В сундуке какого цвета лежит оружие, если зелёный сундук стоит левее, чем синий?
Решение :
ДК - зелёный
ЗC - красный
О - синий
Задача 20
Девять осликов за 3 дня съедают 27 мешков корма.
Сколько корма надо пяти осликам на 5 дней?
Решение :
1 шаг 9 осликов в 1 день - 27 : 3= 9м.
2 шаг 1 ослик в 1 день - 9 : 9 = 1 м.
3 шаг 5 осликов в 1 день - 5 * 1 = 5 м.
4 шаг 5 осликов за 5 дней - 5 * 5 = 25 м.
Задача 21
Кенгуру мама прыгает за 1 секунду на 3 метра, а её маленький сынишка прыгает на 1 метр за 0,5 секунды.
Они одновременно стартовали от бассейна к эвкалипту по прямой.
Сколько секунд мама будет ждать сына под деревом, если расстояние от бассейна до дерева 240 метров
Решение :
1 шаг 240 : 3 = 80 (с) скакала мама Кенгуру
2 шаг сын за 0,5 с - 1 м, за 1 с - 2 м
3 шаг 80 * 2 = 160 (м) проскачет кенгурёнок за 80 с
4 шаг 240 - 160 = 80 (м) осталось проскакать кенгурёнку когда
мама уже под эвкалиптом
5 шаг 80 : 2 = 40 (с)
Ответ: 40 секунд.
Задача 22
На скотном дворе гуляли гуси и поросята.
Мальчик сосчитал количество голов, их оказалось 30, а затем он сосчитал количество ног, их оказалось 84.
сколько гусей и сколько поросят было на школьном дворе?
Решение :
1 шаг Представьте, что все поросята подняли по две ноги вверх
2 шаг на земле осталось стоять 30 * 2 = 60 ног
3 шаг подняли вверх 84 - 60 = 24 ноги
4 шаг подняли 24 : 2 = 12 поросят
5 шаг 30 - 12 = 18 гусей
Ответ: 12 поросят и 18 гусей.
ЗАДАЧА 23
Часы Юры отстают на 8 минут, но он считает, что часы спешат на 2 минуты. Часы Коли спешат на 2 минуты, однако он думает, что они отстают на 8 минут. Друзья договорились, что встретиться в 5 часов вечера. Кто раньше окажется у места встречи и на сколько минут
РЕШЕНИЕ: Отметим, что мальчики приходят в точку встречи по своему «внутреннему» таймеру (который рассчитывают), а не по реальному. Поэтому надо узнать, каково реальное время в момент прихода каждого. Найдем разницу между реальным временем и тем временем, которое представляет себе Юра. Пусть точное время x минут, тогда на часах Юры x-8 минут. Так как он думает, что они спешат, значит считает, что сейчас x-8-2 минут. Поэтому значение реального времени больше того, которое представляет себе Юра на 10 минут. Это означает, что к моменту прихода Юры в точку встречи реальное время составит 17ч 10 мин.
Аналогично рассуждая можно получить расклад по Коле. Пусть y (мин) — реальное время. Тогда часы Коли в этот момент показывают y+2 (мин). Так как он думает, что часы отстают на 8 минут, значит считает, что в этот момент y+2+8 минут.
Поэтому значение реального времени меньше представляемого Колей на 10 минут. Это значит, что к моменту прихода Коли реально 16ч 50 мин. Поэтому Коля пришел раньше Юры на 20 минут.
ЗАДАЧА 24
Петя в трамвае заметил Васю, который поравнялся с трамваем следуя вдоль трамвайных путей в противоположном направлении. Через минуту Петя вышел и побежал вдогонку за Васей вдвое быстрее его, но в 4 раза медленнее трамвая. Через какое время Петя догонит Васю? Помогите.
РЕШЕНИЕ: Прежде всего, нужно понять, что означает «в два раза быстрее». Это значит, что скорость больше в два раза. А поэтому в два раза больше будет пройденное расстояние (не важно, за какое время). Тогда, если Петя идет в два раза быстрее Васи и в 4 раза медленнее трамвая, то Вася проходит за минуту в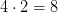 
раз меньшее расстояние, чем трамвай.
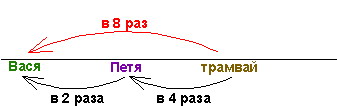Поэтому если за одну минуту Вася проходит какой-то отрезок пути, то трамвай проезжает 8 таких отрезков. Поэтому расстояние между мальчиками в момент выхода Пети составляет 9 отрезков. За ту же минуту Петя проходит 2 отрезка (раз его скорость в 2 раза больше). Введем единицу измерения длины, равную этому же отрезку. Тогда мы имеем стандартные начальные данные для самой обычной задачи на скорость сближения. Скорости мальчиков известны – это 1 (отрезок/мин) и 2 (отрезка/мин), а расстояние для сближения составляет 9 отрезков.
За каждую минуту оно сокращается на 2-1=1 отрезок (это и есть скорость сближения). А нам надо узнать, за какое время расстояние в 9 отрезков сократится до нуля, то есть надо узнать время сближения. Его можно найти, разделив путь сближения на скорость сближения. Поэтому 9 делим на 1 и получаем 9 минут. Ответ: 9 мин.
ЗАДАЧА 25
Cвете втрое больше лет, чем было Максиму тогда, когда она была в его нынешнем возрасте. Когда Максим будет в возрасте Светы, то им вместе будет 28лет. Сколько сейчас лет Максиму и сколько сейчас лет Свете?
РЕШЕНИЕ: Запутанные (олимпиадные) задачи на возраст удобно показывать на временной оси, на которой возраста представляются точками. Если у нас 2 человека и их возраста меняются, то изображающие их точки будут просто двигаться по оси. При этом расстояние между ними (разница в возрасте) будет сохраняться. Покажем нынешний возраст Светы и Максима точками С и М (верхний ряд букв на рисунке). В нижнем ряду поставим буквы С и М для того момента, когда «Света была в нынешнем возрасте Максима». Получим равные отрезки, концы которых (нижняя М и верхняя С) согласно условию «в 3 раза» можно обозначить как х и 3х. Тогда нынешний возраст Максима (середина отрезка) будет иметь координату 2х, а значит разница в возрасте составит ровно х (лет). Теперь покажем, какими будут координаты возрастов в тот момент, когда Максим окажется в возрасте Светы. Эти буквы стоят в ряду «будущее». Длина их отрезка тоже равна х (лет) и поэтому возраст Светы в этот момент окажется равным 4х (лет). Так как в будущем им вместе будет 28 лет, то 3х+4х=28, откуда получаем, что х=4. Поэтому Максиму сейчас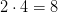 
лет, а Свете сейчас 
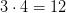лет.
ЗАДАЧА 26:
решить олимпиадную задачку за 5 — 6 класс. Вася написал в тетради 4 числа. Сложил их по два всеми возможными способами получил шесть таких сумм: 2, 4, 9, 9, 14, 16. Какие числа записал Вася?
РЕШЕНИЕ: Пусть a, b, с, d – искомые числа, расположенные в порядке возрастания. Составим последовательность их суммы также в порядке возрастания используя неравенство a < b < c < d. Получим такой ряд:
1) a+b=2
2) a+c=4
3,4) b+c и a+d
5) b+d=14
6) c+d=16
Первые две суммы явно наименьшие и поэтому равны 2 и 4. Две последние явно наибольшие и равны соответственно 14 и 16. Осталось выяснить судьбу двух оставшихся: b+с и a+d. Но так на них приходятся две девятки, то каждая из них равна 9. По первым двум суммам делаем вывод, что с на 2 больше чем b. Поэтому c=b+2. Подставляя выражение для числа с в равенство b+c=9 получим, что b+b+2=9. Поэтому b=3,5 и значит c=3,5+2=5,5. Из первого равенства вытекает, что a=2-3,5=-1,5, а из последнего, что d=16-5,5=10,5
В итоге ответ оказывается таким: -1,5; 3,5; 5,5 и 10,5
ЗАДАЧА 27
Всего 5555 человек, на 10 солдат приходится 1 капрал, на 5 капралов 1 офицер, на 9 офицеров 1 генерал. Решение: сколько всего было солдат?
РЕШЕНИЕ:
Для начала определим, сколько человек в одном таком «наборе», состоящем из генерала, капралов, офицеров и солдат.
Один генерал и девять офицеров у нас уже есть. Так как на каждого офицера приходится 5 капралов, то на 9 офицеров приходится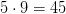 
капралов.
Так как на каждого капрала приходится 10 солдат, то на 45 капралов приходится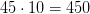 
солдат.
Всего человек в «наборе»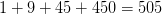 
Так как всего в армии 5555 человек, то количество «наборов» равно
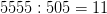. В одном «наборе» 
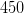солдат, поэтому в 11 «наборах» будет 
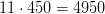солдат.
Ответ: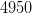 
солдат.
Задача 28
. В несколько одинаковых автобусах 115 человек поехали на озеро, 138 - в лес. Все места в автобусах были заняты, и всем хватило места. Сколько было заказано автобусов и сколько мест в каждом автобусе? (1)
Решение:
Поскольку мест в автобусах не осталось, число детей, выехавших в каждом из двух направлений, кратно числу мест в автобусе. Следовательно, число мест в автобусе - общий делитель чисел 115 и 138. Для отыскания общего делителя воспользуемся правилом : общий делитель двух чисел является также общим делителем этих чисел и их разности.
138 - 115 = 23. Всего автобусов с детьми было:
(115 + 138)/23 = 11 автобусов.
Ответ: 11 автобусов
Задача 28
. Как при помощи только пяти цифр 5, знаков арифметических действий и скобок представить каждое из чисел от 0 до 10 включительно?(1)
Решение. Например:
1. 0=(5-5)*(5+5+5)
2. 1=5:5+(5-5)*5
3. 2=(5+5):5+5-5
4. 3=(5*5-5-5):5
5. 4=5-5:5+5-5
6. 5=5+(5-5)*(5+5)
7. 6=5+5:5+5-5
8. 7=5+5:5+5:5
9. 8=5+(5+5+5):5
10. 9=(5*5-5):5+5
11. 10=5+5+(5-5)*5
Задача 29
. После 7 стирок длина, ширина и высота куска хозяйственного мыла, имеющего форму прямоугольного параллелепипеда, уменьшились вдвое. На сколько стирок хватит оставшегося мыла?(1)
Решение:
Нарисовав кусок мыла и поделив каждую сторону пополам, видим, что получится 8 маленьких кусочков, каждый из которых равен оставшемуся после 7 стирок. То есть на 7 стирок ушло мыла столько, сколько было в остальных 7 кусочках, поэтому остатка хватит ровно на одну стирку.
Ответ. Оставшегося мыла хватит на одну стирку.
Задача 30
. Четыре утёнка и пять гусят весят 4 килограмма 100 грамм, а пять утят и четыре гусенка весят 4 килограмма. Сколько весит 1 утенок? (3)
Решение:
4утенка + 5 гусят=4100грамм
5утят + 4гусят =4000, значит 9 утят и 9 гусят весят 8100 грамм, 1 утенок и 1 гусенок 8100:9=900 грамм, тогда 4 утят и 4 гусят 900*4=3600 грамм, 4000-3600=400 грамм весит 1 утенок
Ответ: 400 грамм
Задача 5. Решите числовой ребус (3)
ОДИН
+
ОДИН
-
МНОГО
Решение: Очевидно, О число чётное, но 2*О больше, чем 10 и поэтому О=6 или О=8, если О =8, то Н=4 и 2*О <15( а должно быть 2*О=16) поэтому, О=6, Н=3, М=1, Д >5 и 2Д=16, значит, Д=8. 2И=Г и И ≤4, но И≠1, так, как М=1; И≠3 или Н=3 И≠4, иначе, Г=Д=8, И≠0, иначе Г=О. тогда И=2, Г=4, получаем
6823
+
6823
________________
13646
Задача 31
. Имеются бревна разной длины. Когда каждое из них распилили на несколько частей, то оказалось, что частей получилось на 25 больше, чем было сделано распилов. Сколько брёвен было первоначально?
Решение: Если бревно распилить на любое число частей , то частей всегда окажется больше, чем распилов. Если частей получилось на 25 больше, чем было распилов, значит, первоначально брёвен было 25.
Ответ: 25
Задача 32
. В день рождения дяди Федора почтальон Печкин хочет выяснить, сколько тому лет. Шарик говорит, что дяде Федору больше 11 лет, а кот Матроскин утверждает, что больше 10 лет. Сколько лет дяде Федору, если известно, что ровно один из них ошибся? Ответ обоснуйте.
Решение: Заметим, что если не ошибся Шарик, то не ошибся и Матроскин, что противоречит условию. Значит, Шарик сказал неправду, в отличие от кота Матроскина. Таким образом, дяде Федору больше 10 лет, но не меньше 11., дяде Федору исполнилось 11 лет.
Ответ: 11 лет.
Задача 33
.Математическая логика .(6)
Когда три подруги — Надя, Валя и Маша — вышли гулять, на них были белое, красное и синее платья. Туфли их были тех же трех цветов, но только у Нади цвета туфель и платья совпадали. При этом у Вали ни платье, ни туфли не были синими, а Маша была в красных туфлях. Определите цвет платьев и туфель каждой из подруг.
Подсказка
У Вали белые туфли — почему?
Решение:
У Вали туфли не синие (по условию) и не красные (красные — у Маши), следовательно, у Вали белые туфли; у Нади, таким образом, оставшиеся синие. Это в свою очередь означает, что у Нади — синее платье (по условию, цвета туфель и платья у Нади совпадают). Тогда у Вали — красное платье, а у Маши — белое (поскольку у них по условию туфли и платья разного цвета, причём не синего, так как всё синее — на Наде). Итак: у Нади туфли и платье синего цвета; у Вали туфли белые, платье красное; у Маши туфли красные, платье белое. 1
Ответ: У Нади туфли и платье синего цвета; у Вали туфли белые, платье красное; у Маши туфли красные, платье белое.
Задача 34
В комнате находятся 85 воздушных шаров — красных и синих. Известно, что: 1) по крайней мере один из шаров красный; 2) из каждой произвольно выбранной пары шаров по крайней мере один синий. Сколько в комнате красных шаров? (6)
Подсказка
Подумайте, может ли в комнате быть два красных шара.
Решение:
Поскольку среди двух любых шаров один синий, то двух красных шаров в комнате быть не может. Значит, в комнате находятся 84 синих воздушных шара и 1 красный.
Ответ 1 шар.
Задача 35
Среди 4-х людей нет трех с одинаковым именем, одинаковым отчеством или одинаковой фамилией, но у любых двух людей совпадают либо имя, либо отчество, либо фамилия. Может ли так быть? .(6)
Подсказка
Попробуйте написать эти имена.
Решение:
Да, так может быть, например: Иван Иванович Иванов, Иван Петрович Петров, Петр Иванович Петров, Петр Петрович Иванов
Ответ: Иван Иванович Иванов, Иван Петрович Петров, Петр Иванович Петров, Петр Петрович Иванов
ЗАДАЧА 36 Сколько трёхзначных чисел можно составить из цифр 2,4,6,8, если цифры в записи числа не повторяются?
Решение: стр. 39 учебника, 4*3*2= 24 трехзначных числа
Задача 37: Сегодня Сереже исполнилось 10 лет, а Вове – 1 год. Каков будет возраст Сережи, когда он станет втрое старше Вовы?
Дата: 2019-07-24, просмотров: 232.
