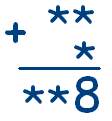
Ответ. 99 + 9 = 108

Задача № 2

 Восстановите поврежденную запись Ответ. 99 + 99 = 198

Задача № 3 :

Решите ребус:

Решение:

Очевидно, Д≤4. В разряде сотен имеем А + А = А, значит, А = 0 (без перехода) или А = 9 (с переходом). Значение А = 0 не подходит, так как в разряде единиц А + А = Р (получаем А = Р = 0). Значит, А = 9, Р = 8, Е = 7. Тогда 2М + 1 = 10 + Т, Т < 9, значит М = 5 или 6 (так как получается переход), а значения 7 и 8 уже заняты буквами Е и Р. При М = 6 получается решение:
18969 + 18969 = 37938.

Ответ:18969 + 18969 = 37938.

Задача № 4         Решите ребус:

Решение:

Так как КА + КА + КА оканчивается на КА, то КА = 50, а значит, К = 5, А = 0. Так как Ш + Ш + Ш + 1 оканчивается на 0, то Ш = 3.

Так как сумма трех чисел, начинающихся на 5 может начинаться лишь с 1, то С = 1.

Рассматривая варианты для О, получаем, что О = 6 или О = 7, а значит, Б = 9 или Б = 2.

Итак, получаем два варианта решения:

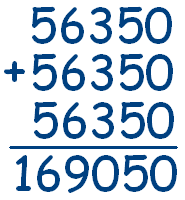и

• Задача № 5         Решите ребус:

Ответ: С = 4; П = 3; Т = 2; Р = 7; К = 8; О = 9.

Задача № 6              Решите ребус, если известно, что наибольшая цифра

в числе СИЛЕН равна 5.

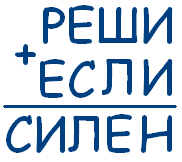
Решение:

Так как наибольшая цифра в числе «СИЛЕН» равна 5, а С = 1, то остальные 4 цифры в данном числе будут 2, 3, 4, 5.

Так как Н < 6, то И = 2. А значит, Н = 4. Так как Л > Е (в самом деле так как Е + 1 = Л, то Л > Е, ведь Л и Е меньше 5 по условию), то Л = 5, Е = 3.

А тогда уже легко находим остальные цифры: Ш = 8, Р = 9.

В итоге получается: 9382 + 3152 = 12534

Ответ: 9382 + 3152 = 12534

 Задача № 7     Решите ребус 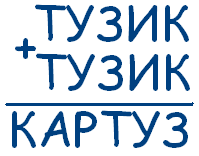Ответ.54271 + 54271 = 108542

Задача № 8                           Решите ребус

• 
  Ответ.3930 + 3980 = 7910 (начать с А = 0, К < 5, так как О + О = О и О ≠ А, то О = 9. Рассматривая К = 1, 2, 3, 4, получим искомое решение).

ГЛАВА У1                  ОЛИМПИАДНЫЕ ЗАДАЧИ:

1. Решите задачу (7 баллов)

На пиратском рынке бочка рома стоит 800 дублонов, или 100 пиастров, а пистолет стоит 100 дублонов, или 250 дукатов. Сколько пиастров нужно заплатить за попугая, если за него просят 100 дукатов?

Решение: Ответ: 5 пиастров

2. Решите задачу (7 баллов)

Три синих попугая капитана Флинта съедают 3кг. корма за три дня, пять зеленых попугаев – 5кг. корма за пять дней, а семь оранжевых – 7кг. корма за семь дней. Какие попугаи самые прожорливые?

• Решение:

· За один день три синих съедают – 1кг. корма, пять зеленых и семь оранжевых тоже съедают в день по 1кг корма.

· Ответ: Синие попугаи самые прожорливые.

3. Решите задачу (7 баллов)

Крепость имеет вид семиугольника, в каждой вершине которого находится сторожевая башня. Каждую из семи стен крепости охраняют стражники в башнях, находящихся в концах этой стены. Какое наименьшее количество стражников нужно разместить в башнях, чтобы каждая стена охранялась не менее чем семью стражниками?

Решение: Комментарии по оцениванию: Занумеруем башни подряд 1, 2, 3,…,7.

Тогда в первой башне находится х₁ стражник, во второй – х₂ стражник, … в седьмой – х₇ стражник. Каждая стена охранялась не менее чем семью стражниками, значит,

х₁+х₂ <7, х₂+х₃ >7 и т.д. Складывая эти неравенства, получим: 2(х₁+х₂+…+х₇) > 49, отсюда (х₁+х₂+…+х₇) > 49:2, поскольку число стражников целое, то оно не может быть меньше 25.

Ответ: 25.

4. Решите задачу (7 баллов)

Пират испортил карту сокровищ, имеющую форму квадрата. Он вырезал из неё восьмиугольник, а 5 отрезанных многоугольников выбросил. Оставшейся восьмиугольник имеет стороны равной длины, и внутренние углы равной величины.

а) Можно ли по этому восьмиугольнику восстановить размеры карты сокровищ?

б) Определите, какую форму могли иметь 5 отрезанных многоугольников.

• Решение:

· Комментарии по оцениванию:

· а) Можно ли по этому восьмиугольнику восстановить размеры карты сокровищ? (3 балла)

· б) Определите, какую форму могли иметь 5 отрезанных многоугольников. (за каждый приведенный пример 2 балла)

· Так как оставшийся кусок имеет форму правильного восьмиугольника, а отрезанных кусков – 5, то они могут иметь не больше одной общей стороны со стороной восьмиугольника. Значит, минимум три стороны восьмиугольника принадлежат квадрату. Поэтому форма искомой карты сокровищ будет квадрат со стороной, равной расстоянию между противоположными сторонами восьмиугольника. Отрезанные многоугольнику будут: 1) 5 треугольников; 2) 4 треугольника и один четырехугольник.

5. Решите задачу (7 баллов)

Робинзон попал на необитаемый остров. Каждый день (начиная с того дня, когда он попал на остров) он вырезал на доске первую букву в названии дня недели на русском языке. На 2013–й день, вырезав букву, он посчитал вырезанные буквы. Оказалось, что разных букв было вырезано разное количество. В ответ запишите день недели, когда Робинзон попал на остров.

Решение: В течение недели Робинзон вырежет на доске по две буквы «п» (понедельник, пятница), «в» (вторник, воскресенье), «с» (среда, суббота) и одну букву «ч» (четверг). Так как 2013=287·7+4=2009+4, то через 2009 дней будет вырезано по 574 буквы «п», «в», «с» и 287букв «ч». Через четыре дня количества букв оказались различными. Для этого нужно, чтобы в эти четыре дня одна из букв «п», «в», «с» появилась дважды, одна – один раз и одна не появлялась. Значит, четвертой появившейся буквой должна быть «ч». Буквы идут в следующем порядке: «п», «в», «с», «ч», «п», «с», «в», «п», «в», «с» …

Таким образом, возможна лишь ситуация: «с», «ч», «п». Это означает, что Робинзон попал на остров в среду.

Ответ: среда

Задачи по математике для 5 - 6 класса с конкурса «Кенгуру» :

Задача № 1 На день рождения пришло двенадцать детей следующих возрастов: 6 лет, 7 лет, 8 лет, 9 лет и 10 лет, причем четырем детям было по 6 лет, а восьмилетних было больше всех. Вычислите их средний возраст.

Решение: Так как число детей младшего возраста равно 4, то число восьмилетних может быть не менее 5. Если их больше 5, то шести и восьмилетних будет больше 9. Тогда на детей возрастов 7 лет, 9 лет и 10 лет останется в сумме только или 1 год или 2 года. Этого быть не может. Значит восьмилетних детей ровно 5 человек. Остаток от 12 составит 3 ребенка. Их надо распределить между возрастами 7 лет, 9 лет и 10 лет. Легко понять, что их ровно по одному человеку.

Получаем следующий расклад: 6 лет — 4 человека; 7 лет — 1 человек; 8 лет — 5 человек; 9 лет — 1 человек;10 лет — 1 человек.

Найдем теперь средний возраст — среднее арифметическое имеющихся возрастов. Напомню, что средним арифметическим нескольких чисел называют результат деления их суммы на их количество. Вычисляем его так: ( 6*4 + 7*1 + 8*5 + 9*1 + 10*1) / 12 = 7,5

Ответ: 7,5 лет.

• Задача № 2 :

Натуральные числа от 1 до 12 расставлены по кругу. Разность любых двух соседних равна 1 или 2. Укажите числа, которые стоят рядом.

А) 5 и 6
Б) 10 и 9
В) 8 и 10
Г) 6 и 7
Д) 4 и 3

Решение: Возьмем старт с единицы: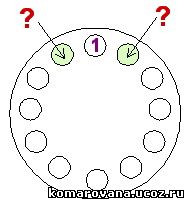

Очевидно, что соседями единички являются числа 2 и 3. Из-за того, что симметричные расклады дают один и тот же ответ, 2 и 3 можно расставить вокруг числа 1 произвольным образом. Запишем, например, слева 2, а справа 3.

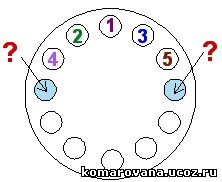Соседним числом д 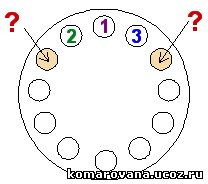ля 2, расположенным в выделенном кружке слева, может быть только число, большее чем 2 (меньшая единица уже задействована). Это 3 или 4. Так как 3 не должно повториться, имеем единственный вариант продолжения — направить число 4 в выделенный правый кружок.У числа 3 вторым соседом будет или 4 или 5. Число 5 повторно использовать нельзя, поэтому единственной возможностью остается постановка сила 5.

Продолжая таким же образом далее получаем окончательно распределение: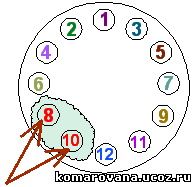

Ответ: 8 и 10.