- Вначале оба кувшина пусты (первый черный столбец).
- Наполним водой кувшин А (второй столбец),
- а затем перельем из него воду в кувшин В (третий столбец).
- Потом эти 5 литров из кувшина В выльем в раковину (четвертый столбец).
- Затем 3 литра воды из кувшина А перельем в кувшин В (пятый столбец).
- Вновь наполним кувшин А водой из под крана (шестой столбец)
- и дольем из него в кувшин В 2 литра, наполнив его до краев (седьмой столбец столбец).
- Выливаем из кувшина В содержимое в раковину (восьмой столбец) — задача решена
Рассмотрим примеры решения задач:
Задача № 1 : Однажды Винни-Пух захотел полакомиться медом и пошел к пчелам в гости. По дороге нарвал букет цветов, чтобы подарить труженицам пчелкам. Пчелки очень обрадовались, увидев мишку с букетом цветов, и сказали: «У нас есть большая бочка с медом. Мы дадим тебе меда, если ты сможешь с помощью двух сосудов вместимостью 3 л и 5 л налить себе 4 л!» Винни-Пух долго думал, но все-таки смог решить задачку. Как он это сделал?
Решение:
Как в результате можно получить 4 л? Нужно из 5-литрового сосуда отлить 1 л. А как это сделать? Нужно в 3-литровом сосуде иметь ровно 2 л. Как их получить? – Из 5-литрового сосуда отлить 3 л.
Решение лучше и удобнее оформить в виде таблицы:
| Ходы | 1 | 2 | 3 | 4 | 5 | 6 |
| 5 л | 5 | 2 | 2 | - | 5 | 4 |
| 3 л | - | 3 | - | 2 | 2 | 3 |
Наполняем из бочки 5-литровый сосуд медом (1 шаг). Из 5-литрового сосуда отливаем 3 л в 3-литровый сосуд (2 шаг). Теперь в 5-литровом сосуде осталось 2 литра меда. Выливаем из 3-литрового сосуда мед назад в бочку (3 шаг). Теперь из 5-литрового сосуда выливаем те 2 литра меда в 3-литровый сосуд (4 шаг). Наполняем из бочки 5-литровый сосуд медом (5 шаг). И из 5-литрового сосуда дополняем медом 3-литровый сосуд. Получаем 4 литра меда в 5-литровом сосуде (6 шаг). Задача решена.
Поиск решения можно было начать с такого действия: к трем литрам добавить 1 литр.
Но тогда решение будет выглядеть следующим образом:
| Ходы | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 5 л | - | 3 | 3 | 5 | - | 1 | 1 | 4 |
| 3 л | 3 | - | 3 | 1 | 1 | - | 3 | - |
Задача № 2 : Бэтмен и Человек-Паук:
Бэтмен и Человек-Паук никак не могли определить, кто из них самый главный супергерой. Что только они не делали: отжимались, бегали 100 метровку, подтягивались – то один победит, то другой. Так и не разрешив свой спор, отправились они к мудрецу. Мудрец подумал и сказал: «Самый главный супергерой – это не тот, кто сильнее, а тот, кто сообразительнее! Вот, кто решит первым задачу, тот и будет самым-самым! Слушайте: имеются два сосуда вместимостью 8 л и 5 л. Как с помощью этих сосудов налить из источника 7 л живой воды?» Помогите вашему любимому герою решить эту задачу.
Решение:
Ход рассуждений таков:
Как в результате получить 7 литров? – Нужно к 5 литрам долить 2 л. А где их взять? – Из 5-литрового сосуда отлить 3 л. А как их получить? В 8 литровый перелить из 5 литрового 5 литров, потом еще три.
Решение задачи показано в таблице:
| Ходы | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 л | - | 5 | 5 | 8 | - | 2 | 7 |
| 5 л | 5 | - | 5 | 2 | 2 | 5 | - |
Задача № 3 :Губка Боб:
Губке Бобу срочно нужно налить из водопроводного крана 6 л воды. Но он имеет лишь два сосуда 5-литровый и 7-литровый. Как ему это сделать?
Решение: Решение задачи представлено в таблице:
| Ходы | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 7 л | 7 | 2 | 2 | - | 7 | 4 | 4 | - | 7 | 6 |
| 5 л | - | 5 | - | 2 | 2 | 5 | - | 4 | 4 | 5 |
Задача № 4 Гарри Поттер:
У Гарри Потера имеются двое песочных часов: на 7 минут и на 11 минут. Волшебное зелье должно варится 15 минут. Как сварить его Гарри Потеру, перевернув часы минимальное количество раз?
Решение: 15 = (11 - 7) + 11. Нужно одновременно перевернуть часы, через 7 минут Гарри начинаем варить зелье. После 4 минут (песок в часах на 11 минут закончится) вновь перевернуть часы на 11 минут.Задача решена.
Задача № 5 Запасливый Винни-Пух:
Летом Винни-Пух сделал запас меда на зиму и решил разделить его пополам, чтобы съесть половину до Нового Года, а другую половину - после Нового года. Весь мед находится в ведре, которое вмещает 6 литров, у него есть 2 пустые банки - 5-литровая и 1-литровая. Может ли он разделить мед так, как задумал?
Решение:
Представлено в таблице:
| Ходы | 1 | 2 | 3 | 4 | 5 | 6 |
| 6 л | 6 | 1 | 1 | 2 | 2 | 3 |
| 5 л | - | 5 | 4 | 4 | 3 | 3 |
| 1 л | - | - | 1 | - | 1 | - |
Задача № 6 Карлсон и варенье:
У Карлсона есть ведро варенья, оно вмещает 7 литров. У него есть 2 пустых ведерка - 4-литровое и 3-литровое. Помогите Карлсону отлить 1 литр варенья к чаю в меньшее (3-литровое) ведерко, оставив 6 литров в большом (7-литровом) ведре.
Решение: Представлено в таблице:
| Ходы | 1 | 2 | 3 | 4 |
| 7 л | 7 | 3 | 3 | 6 |
| 4 л | - | 4 | 1 | 1 |
| 3 л | - | - | 3 | - |
Задача № 7
Отмерить 3 л, имея сосуд 5 л.
Какое наименьшее число переливаний потребуется для того, чтобы в четырехлитровую кастрюлю с помощью крана и пятилитровой банки налить 3 литра воды?
Решение
Наливаем кастрюлю.
Переливаем воду из кастрюли в банку.
Наливаем кастрюлю.
Доливаем полную банку, и в кастрюле остается 3 литра.
Задача № 8
Деление 10 л поровну, имея сосуды 3, 6 и 7 л.
Разделить на 2 равные части воду, находящуюся в 6-литровом сосуде (4 л) и в 7-литровом (6 л), пользуясь этими и 3-литровым сосудами.
Какое наименьшее количество переливаний потребуется?
Решение задачи 2.
В скобках – второй вариант решения.
| Сосуд 6 л | Сосуд 3 л | Сосуд 7 л | |
| До переливания | 4 | 0 | 6 |
| Первое переливание | 1 (4) | 3 (3) | 6 (3) |
| Второе переливание | 1 (6) | 2 (1) | 7 (3) |
| Третье переливание | 6 (2) | 2 (1) | 2 (7) |
| Четвертое переливание | 5 (2) | 3 (3) | 2 (5) |
| Пятое переливание | 5 (5) | 0 (0) | 5 (5) |
Задача № 9.
Деление 8 л поровну, имея сосуды 8, 5 и 3 л.
Разделить на две равные части воду, находящуюся в полном 8 литровом сосуде, пользуясь этим и пустыми 5- и 3-литровыми сосудами.
Какое наименьшее количество переливаний потребуется?
Решение :
| Сосуд 8 л | Сосуд 5 л | Сосуд 3 л | |
| До переливания | 8 | 0 | 0 |
| Первое переливание | 3 | 5 | 0 |
| Второе переливание | 3 | 2 | 3 |
| Третье переливание | 6 | 2 | 0 |
| Четвертое переливание | 6 | 0 | 2 |
| Пятое переливание | 1 | 5 | 2 |
| Шестое переливание | 1 | 4 | 3 |
| Седьмое переливание | 4 | 4 | 0 |
Задача № 10:.
Деление 16 л поровну, имея сосуды 6, 11 и 16 л.
Разделить на две равные части воду, находящуюся в полном 16 литровом сосуде, пользуясь этим и пустыми 11- и 6-литровыми сосудами.
Какое наименьшее количество переливаний потребуется?
| Сосуд 16 л | Сосуд 11 л | Сосуд 6 л | |
| До переливания | 16 | 0 | 0 |
| Первое переливание | 10 | 0 | 6 |
| Второе переливание | 10 | 6 | 0 |
| Третье переливание | 4 | 6 | 6 |
| Четвертое переливание | 4 | 11 | 1 |
| Пятое переливание | 15 | 0 | 1 |
| Шестое переливание | 15 | 1 | 0 |
| Седьмое переливание | 9 | 1 | 6 |
| Восьмое переливание | 9 | 7 | 0 |
| Девятое переливание | 3 | 7 | 6 |
| Десятое переливание | 3 | 11 | 2 |
| Одиннадцатое переливание | 14 | 0 | 2 |
| Двенадцатое переливание | 14 | 2 | 0 |
| Тринадцатое переливание | 8 | 2 | 6 |
| Четырнадцатое переливание | 8 | 8 | 0 |
Задача № 11.
Два сосуда и кран с водой.
Какое наименьшее число переливаний необходимо для того, чтобы с помощью 7- и 11-литровых сосудов и крана с водой отмерить 2 л?
Если сначала наполнить 11-литровый сосуд, то потребуется 18 переливаний, а если 7-литровый, то, как следует из рисунка, – всего 14.
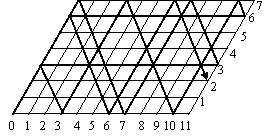
Задачи "на переливание" более чем увлекательные. Один из методов их решения - "от конца к началу". Нужно исходить из того, что надо получить.
Задача № 12. Как, пользуясь банками в 3 л и 5 л, набрать воды ровно 1 л?
Решение:
| Сосуды | Переливания | |||
| 5 литров | - | 3 | 3 | 5 |
| 3 литра | 3 | - | 3 | 1 |
Задача № 13 Как отмерить 4 л воды с помощью сосудов в 3 л и 5 л?
Решение:
| Сосуды | Переливания | |||||||
| 5 литров | - | 3 | 3 | 5 | - | 1 | 1 | 4 |
| 3 литра | 3 | - | 3 | 1 | 1 | - | 3 | - |
Задача № 14 . Как, имея лишь два сосуда емкостью 5 л и 7 л, отмерить 6 л воды?
Решение:
| Сосуды | Переливание | |||||||||
| 7 литров | 7 | 2 | 2 | - | 7 | 4 | 4 | - | 7 | 6 |
| 5 литров | - | 5 | - | 2 | 2 | 5 | - | 4 | 4 | 5 |
Задача № 15 Набрать 7 л воды из речки.
У подножья высокого холма, на берегу тихой речки был небольшой аул. Жили в нем два брата-охотника. Старшего брата звали Каалка, младшего Копчон. Отправляет старший брат младшего за водой и дает ему два бурдюка, вместимостью 8л и 5л и просит принести ровно 7л воды. Сможет ли Копчон выполнить просьбу старшего брата?
Решение:
| Ходы | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8л | – | 5 | 5 | 8 | – | 2 | 7 |
| 5л | 5 | – | 5 | 2 | 2 | 5 | – |
Задача № 15. Молоко из Простоквашино.
Дядя Федор собрался ехать к родителям в гости и попросил у кота Матроскина 4 л простоквашинского молока. А у Матроскина только 2 пустых бидона: трехлитровый и пятилитровый. И восьмилитровое ведро, наполненное молоком. Как Матроскину отлить 4 литра молока с помощью имеющихся сосудов?
Решение:
Переливаем из 8-литрового ведра 5 литров молока в 5-литровое. Переливаем из 5-литрового бидона 3 литра в 3-литровый бидон.
Переливаем их теперь в 8-литровое ведро. Итак, теперь 3-литровое ведро пусто, в 8-литровом 6 литров молока, а в 5-литровом - 2 литра молока.
Переливаем 2 литра молока из 5-литрового бидона в 3-литровый, а потом наливаем 5 литров из 8-литрового ведра в 5-литровый бидон. Теперь в 8-литровом 1 литр молока, в 5-литровом - 5, а в 3-литровом - 2 литра молока.
Доливаем дополна 3-литровый бидон из 5-литрового и переливаем эти 3 литра в 8-литровое ведро. В 8-литровом ведре стало 4 литра, так же, как и в 5-литровом бидоне. Задача решена.
| сосуд 8 л | сосуд 5 л | сосуд 3 л | |
| До переливания | 8 | 0 | 0 |
| Первое переливание | 3 | 5 | 0 |
| Второе переливание | 3 | 2 | 3 |
| Третье переливание | 6 | 2 | 0 |
| Четвертое переливание | 6 | 0 | 2 |
| Пятое переливание | 1 | 5 | 2 |
| Шестое переливание | 1 | 4 | 3 |
| Седьмое переливание | 4 | 4 | 0 |
После переливания, оказалось, по 4 л молока в 8-литровом и 5-литровом сосудах, а это и требовалось.
Задача № 16 Переливание
Имеется 3 сосуда: 8л 5л 3л.
Первый из них заполнен водой.
Нужно оставить ровно 4л. в первом сосуде.
| 8л 5л 3л | 8л 5л 3л |
| 8 0 0 3 5 0 3 2 3 6 2 0 6 0 2 1 5 2 1 4 3 4 4 0 | 8 0 0 5 0 3 5 3 0 2 3 3 2 5 1 7 0 1 7 1 0 4 1 3 |
Задача № 17 : Как отметить 4л воды с помощью сосудов в 3л и 5 л?
| сосуды | ||||||||
Переливания
Задача № 18 : Как, имя лишь два сосуда емкостью 5л и 7 л, отметить6л воды?
| сосуды |
Переливания | |||||||||
| 7 литров | 7 | 2 | 2 | - | 7 | 4 | 4 | - | 7 | 6 |
| 5 литра | - | 5 | - | 2 | 2 | 5 | - | 4 | 4 | 5 |
.Задача № 19:
Каким образом из реки можно принести ровно 6л воды, если имеется только два ведра: одно – емкостью 4л. другое – 9л?
| сосуды |
Переливания | |||||||
| 9 литров | 9 | 5 | 5 | 1 | 1 | - | 9 | 6 |
| 4 литра | - | 4 | - | 4 | - | 1 | 1 | 4 |
Задача № 20: Бидон емкостью 10л заполнен молоком. Требуется перелить из этого бидона 5л в семилитровый бидон, используя при этом еще один бидон, вмещающий 3л.
| сосуды |
Переливания | |||||||
| 10 литров | 3 | 3 | 6 | 6 | 9 | 9 | 2 | 2 |
| 7 литров | 7 | 4 | 4 | 1 | 1 | - | 7 | 5 |
| 3 литра | - | 3 | - | 3 | - | 1 | 1 | 3 |
Задача № 21: Имея два бидона емкостью 4л и 5л, можно ли налить в ведро 3л воды. Если емкость ведра не менее 3л?
| сосуды |
Переливания | ||||
| 5 литров | - | 4 | 4 | 5 | 5 |
| 4 литров | 4 | - | 4 | 3 | - |
| 3 литра и более | - | - | - | - | 3 |
Задача № 22: ( задача Пуассона) Известному французскому математику Симону Пуассону(1981-1840) в юности предложили задачу. Заинтересовавшись ею, Пуассон затем увлекся математикой и посвятил этой науке всю свою жизнь. Вот эта задача. Некто имеет 12 пинт вина и хочет отлить из этого количества половину, но у него нет сосуда в 6 пинт. Зато есть два других сосуда: в 8 пинт и 5 пинт. Спрашивается: каким образом налить 6 пинт в сосуд на 8 пинт?
| сосуды |
Переливания | |||||||
| 12 пинт | 12 | 4 | 4 | 9 | 9 | 1 | 1 | 6 |
| 8 пинт | - | 8 | 3 | 3 | - | 8 | 6 | 6 |
| 5 пинт | - | - | 5 | - | 3 | 3 | 5 | - |
Задача № 23 :
Как, имея два ведра 14 и 15 литров, набрать из реки 7 литров воды?
Убедитесь что с помощью этих ведер можно набрать любое количество литров,
выраженное натуральным числом меньше 14. 
Набрали 15 литров и перелили из ведра в 14-литровое.
| стало | 1 | 14 |
| осталось | 1 | вылили всё 0 |
| перелили из 1-го во 2-е | 0 | 1 |
| набрали | 15 | 1 |
| перелили 13л во 2-е | 2 | 1+13=14 |
| 2 | вылили 0 | |
| перелили 2 литра | 0 | 2 |
| набрали в первое | 15 | 2 |
| перелили 12 во 2-е | 3 | 2+12=14 - вылили |
| 3 | 0 |
И так далее. В большом ведре получили 1 литр, затем 2, затем 3 литра.
Продолжая дальше наливать и переливать, получим любое целое количество литров от 1 до 15.
Дата: 2019-07-24, просмотров: 323.