Тема № 13. Дифференциальные уравнения первого порядка.
Задачи, приводящие к дифференциальным уравнениям.
Дифференциальное уравнение первого порядка. Общее и частное решение дифференциального уравнения первого порядка. Интегральные кривые.
Теорема Коши. Задача Коши и ее геометрическая интерпретация.
Дифференциальные уравнения с разделяющимися переменными.
Линейные дифференциальные уравнения первого порядка.
Уравнения Бернулли.
Тема № 14. Дифференциальные уравнения высших порядков.
Дифференциальные уравнения высших порядков, их решения.
Задача Коши.
Дифференциальные уравнения второго порядка, допускающие понижения порядка.
Линейные дифференциальные уравнения высших порядков с постоянными коэффициентами. Основные понятия.
Решение однородных линейных дифференциальных уравнений высших порядков с постоянными коэффициентами.
Решение неоднородных линейных дифференциальных уравнений высших порядков с постоянными коэффициентами и специальной правой частью.
Решение неоднородных линейных дифференциальных уравнений высших порядков методом вариации произвольной постоянной.
Раздел № 9. Ряды
Тема № 15. Числовые ряды.
Числовые ряды. Сходимость числового ряда. Свойства сходящихся числовых рядов.
Необходимый признак сходимости знакоположительного ряда. Достаточный признак расходимости ряда.
Достаточные признаки сходимости знакоположительных рядов: признак Даламбера, признак Коши, интегральный признак.
Знакопеременные и знакочередующиеся ряды.
Признак Лейбница. Исследование сходимости знакочередующихся рядов.
Тема №16. Степенные ряды.
Степенной ряд, область его сходимости. Свойства степенных рядов
Теорема Абеля.
Интервал и радиус сходимости степенного ряда. Исследование сходимости степенных рядов.
Ряд Тейлора. Остаточный член ряда Тейлора. Ряд Маклорена.
Разложение некоторых элементарных функций в ряды Тейлора и Маклорена.
Ряды Фурье. Разложение функций в ряды Фурье.
IV . ЗАДАНИЯ ДОМАШНЕЙ КОНТРОЛЬНОЙ РАБОТЫ
Примечание. Номер варианта N заданий домашней контрольной работы соответствует номеру по порядку студента в классном журнале учёта успеваемости.
Линейная алгебра и аналитическая геометрия
Вариант № 1
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) .
1. Найти матрицу С =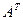 
- 3В, где А = 
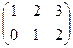; В = 
2. Найти решение матричного уравнения ХА=В, имеющего вид:
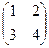Х =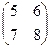 
и сделать проверку.
3. Вычислить:
а)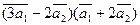 
;
б)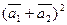 
,
где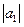 
= 3;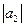 
= 4; угол между векторам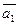и 
и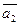 
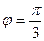
4. Даны векторы 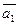(4; 2; -4) и 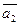(6; -3;2).
Вычислить
а)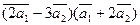 
;
б)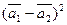 
.
5. Даны векторы 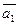(3; -1; 2) и 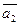(1; 2;-1).
Вычислить векторное произведение:
а)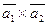 
;
б)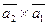 
.
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (4;5) и В ( -1; 7).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
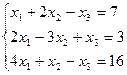
Вариант № 2
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С = 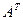- 3В, где А = 
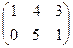; В = 
2. Найти решение матричного уравнения XА = В, имеющего вид:
Х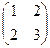 
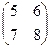= и сделать проверку.
3. Вычислить:
а)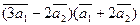 
;
б) ,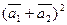
где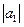 
= 3;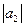 
= 4; угол между векторам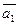и и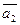 
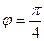
4. Даны векторы 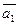(4; 2; -4) и 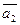(6; -3;2).
Вычислить
а) ;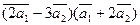
б)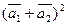 
.
5. Даны векторы 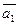(3; -4; 2) и 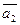(0; 2;-1).
Вычислить векторное произведение:
а) ;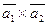
б) .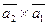
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (5;-9) и В ( 3; 3).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
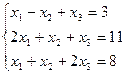
Вариант № 3
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С = А - 4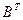 
, где А = 
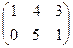; В = 
2.Найти решение матричного уравнения ХА=В, имеющего вид:
Х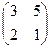 
= 
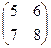и сделать проверку.
3.Вычислить:
а) ;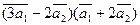
б)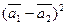 
,
где 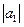= 3; 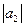= 4; угол между векторам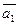и и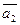 
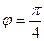
4. Даны векторы 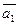(4; 2; -4) и 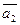(6; -3;2).
Вычислить
а)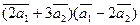 
;
б) .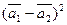
5. Даны векторы 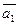(1; -4; 1) и 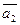(7; 2;-8).
Вычислить векторное произведение:
а)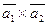 
;
б)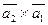 
.
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (2;-6) и В ( 7; 0).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
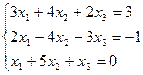
Вариант № 4
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С = А - 4 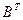, где А = 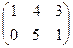; В = 
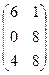
2.Найти решение матричного уравнения АХ=В, имеющего вид:
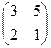Х =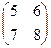 
и сделать проверку.
3.Вычислить:
а)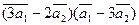 
;
б) ,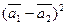
где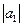 
= 2;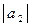 
= 4; угол между векторам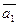и 
и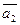 
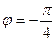
4. Даны векторы 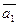(4; 2; -4) и 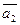(6; -3;0).
Вычислить
а) ;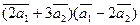
б)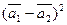 
.
5. Даны векторы 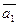(1; -1; 1) и 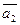(5; 2;-8).
Вычислить векторное произведение:
а) ;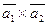
б) .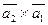
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (-3;-3) и В ( 1; 2).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
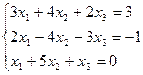
Вариант № 5
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С = 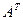– 4В, где А = 
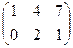; В = 
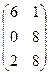
2. Найти решение матричного уравнения АХ=В, имеющего вид:
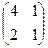Х =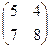 
и сделать проверку.
3. Вычислить:
а)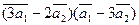 
;
б) ,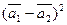
где 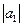= 2; 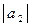= 4; угол между векторам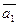и и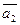
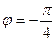
4. Даны векторы 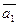(4; 2; -4) и 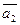(4; -3;2).
Вычислить
а)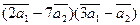 
;
б) .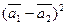
5. Даны векторы 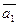(1; -1; 4) и 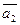(5; -2;8).
Вычислить векторное произведение:
а)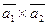 
;
б) .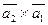
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (3;-4) и В ( 2; 3).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
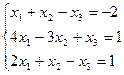
Вариант № 6
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С =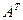 
– 4В, где А = 
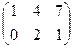; В = 
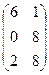
2.Найти решение матричного уравнения АХ=В, имеющего вид:
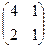Х =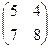 
и сделать проверку.
3.Вычислить:
а)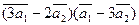 
;
б)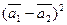 
,
где 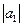= 3;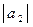 
= 4; угол между векторам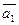и 
и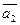 
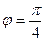
4. Даны векторы 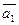(4; 0; -4) и 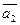(6; -3;5).
Вычислить
а)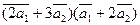 
;
б) .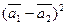
5. Даны векторы 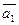(1; -4; 1) и 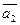(5; 2;-8).
Вычислить векторное произведение:
а) ;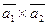
б)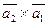 
.
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (8;-7) и В ( 4; 3).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
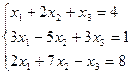
Вариант № 7
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С = 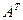– 4В, где А = 
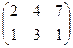; В = 
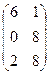
2.Найти решение матричного уравнения АХ=В, имеющего вид:
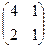Х = 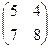и сделать проверку.
3.Вычислить:
а) ;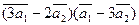
б) ,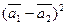
где 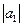= 2; 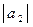= 4; угол между векторами 
и 
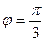
4. Даны векторы (4; 2; -4) и (6; -3;0).
Вычислить
а)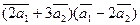 
;
б) .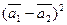
5. Даны векторы (1; -1; 1) и (5; 2;-8).
Вычислить векторное произведение:
а)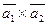 
;
б)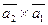 
.
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (-2;-8) и В ( 5; 3).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
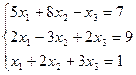
Вариант № 8
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С = 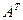– 4В, где А = 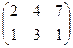; В =
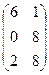
2. Найти решение матричного уравнения АХ=В, имеющего вид:
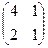Х =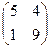 
и сделать проверку.
3.Вычислить:
а) ;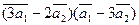
б)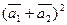 
,
где 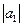= 2; 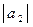= 4; угол между векторами и 
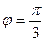
4. Даны векторы (4; 2; -4) и (6; -3;0).
Вычислить
а) ;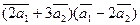
б) .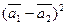
5. Даны векторы (1; -1; 1) и (4; 1;-3).
Вычислить векторное произведение:
а) ;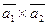
б) .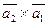
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (3;-6) и В ( 6; 3).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
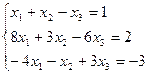
Вариант № 9
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ). Множества
1. Найти матрицу С =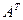 
– 4В, где А = 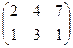; В =
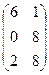
2. Найти решение матричного уравнения АХ=В, имеющего вид:
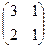Х =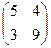 
и сделать проверку.
3. Вычислить:
а)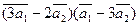 
;
б) ,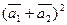
где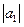 
= 2;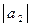 
= 4; угол между векторами и 
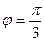
4. Даны векторы (4; 2; -4) и (6; -3;0).
Вычислить
а) ;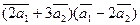
б) .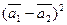
5. Даны векторы (1; -1; 1) и (4; 1;-3).
Вычислить векторное произведение:
а) ;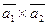
б) .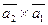
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (3;-8) и В ( -2; 3).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
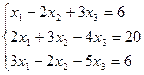
Вариант № 10
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С = А - 4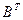 
, где А = 
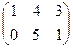; В = 
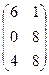
2.Найти решение матричного уравнения АХ=В, имеющего вид:
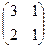Х = 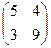и сделать проверку.
3. Вычислить:
а)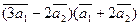 
;
б)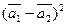 
,
где 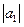= 2; 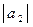= 5; угол между векторами и 
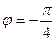
4. Даны векторы (4; 2; -4) и (6; -3;2).
Вычислить
а) ;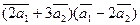
б) .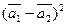
5. Даны векторы (1; -4; 1) и (7; 2;-8).
Вычислить векторное произведение:
а) ;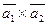
б) .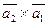
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (-5;-5) и В ( 8; 1).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
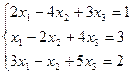
Вариант № 11
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) .
1. Найти матрицу С = 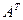- 3В, где А = 
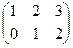; В = 
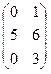
2. Найти решение матричного уравнения ХА=В, имеющего вид:
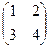Х = 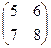и сделать проверку.
3. Вычислить:
а)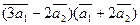 
;
б)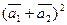 
,
где 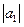= 4;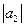 
= 4; угол между векторами и 
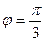
4. Даны векторы (5; 2; -5) и (3; -3;2).
Вычислить
а)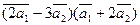 
;
б) .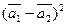
5. Даны векторы (0; -1; -2) и (1; 2;-4).
Вычислить векторное произведение:
а) ;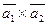
б) .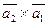
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (4;3) и В ( -1; 1).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
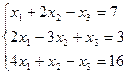
Вариант № 12
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С = 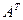- 3В, где А = 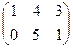; В = 
2. Найти решение матричного уравнения XА = В, имеющего вид:
Х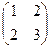 
= 
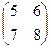и сделать проверку.
3. Вычислить:
а) ;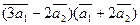
б) ,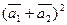
где 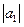= 5;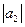 
= 4; угол между векторами и 
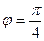
4. Даны векторы (3; 2; -3) и (2; -3;2).
Вычислить
а)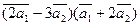 
;
б)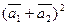 
.
5. Даны векторы (3; 0; 2) и (0; 2;-2).
Вычислить векторное произведение:
а)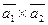 
;
б)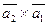 
.
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (3;-4) и В ( 3; 3).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
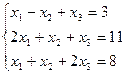
Вариант №1 3
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С = А - 4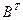 
, где А = 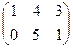; В = 
2.Найти решение матричного уравнения ХА=В, имеющего вид:
Х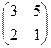 
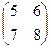= и сделать проверку.
3.Вычислить:
а) ;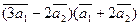
б) ,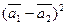
где 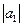= 2; 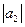= 4; угол между векторами и
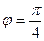
4. Даны векторы 
(5; 2; -1) и (6; -1;2).
Вычислить
а)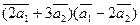 
;
б) .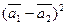
5. Даны векторы (1; -4; 1) и (6; -2;-1).
Вычислить векторное произведение:
а) ;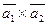
б) .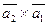
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (2;-2) и В ( 5; 0).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
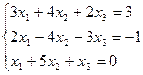
Вариант № 1 4
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С = А - 4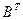 
, где А = 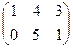; В =
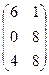
2.Найти решение матричного уравнения АХ=В, имеющего вид:
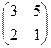Х = 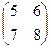и сделать проверку.
3.Вычислить:
а) ;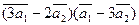
б)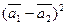 
,
где 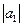= 1;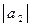 
= 4; угол между векторами и
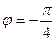
4. Даны векторы (4; 2; -4) и 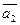(6; -3;1).
Вычислить
а) ;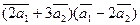
б) .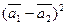
5. Даны векторы (2; -1; 2) и (5; 2;-0).
Вычислить векторное произведение:
а) ;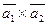
б) .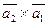
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (-3;-1) и В ( 2; 2).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
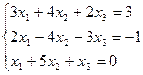
Вариант № 1 5
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С =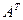 
– 4В, где А = 
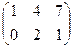; В = 
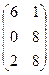
2. Найти решение матричного уравнения АХ=В, имеющего вид:
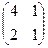Х =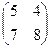 
и сделать проверку.
3. Вычислить:
а)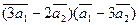 
;
б)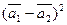 
,
где 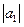= 1; 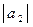= 6; угол между векторами 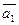и
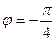
4. Даны векторы (3; 2; -3) и 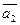(1; -3;1).
Вычислить
а)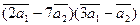 
;
б) .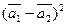
5. Даны векторы (1; -1; 2) и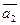 
(5; -3;8).
Вычислить векторное произведение:
а) ;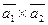
б) .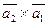
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (3;-2) и В ( 2; -3).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
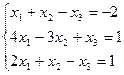
Вариант № 16
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С = 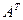– 4В, где А = 
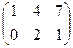; В = 
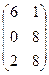
2.Найти решение матричного уравнения АХ=В, имеющего вид:
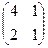Х = 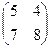и сделать проверку.
3.Вычислить:
а)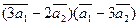 
;
б) ,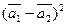
где 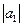= 3; 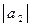= 4; угол между векторами и
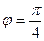
4. Даны векторы (2; 1; -2) и (5; -3;5).
Вычислить
а)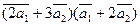 
;
б) .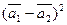
5. Даны векторы (1; -1; 1) и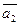 
(5; 2;-0).
Вычислить векторное произведение:
а) ;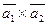
б) .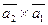
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (8;-7) и В ( 4; 3).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
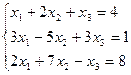
Вариант № 17
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С =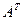 
– 4В, где А = 
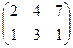; В =
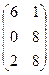
2.Найти решение матричного уравнения АХ=В, имеющего вид:
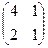Х = 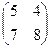и сделать проверку.
3.Вычислить:
а) ;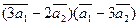
б) ,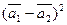
где 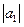= 2;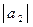 
= 4; угол между векторам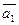и и
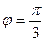
4. Даны векторы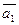 
(4; 2; -2) и (6; -3;1).
Вычислить
а)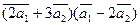 
;
б) .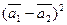
5. Даны векторы (1; -2; 1) и (5; 0;-8).
Вычислить векторное произведение:
а) ;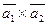
б) .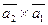
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (-2;-2) и В ( 5; 3).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
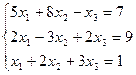
Вариант № 18
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С = 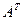– 4В, где А = 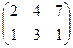; В =
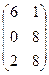
2. Найти решение матричного уравнения АХ=В, имеющего вид:
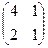Х =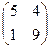 
и сделать проверку.
3.Вычислить:
а) ;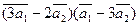
б) ,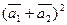
где 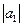= 2; 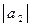= 4; угол между векторами и
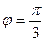
4. Даны векторы (1; 2; -1) и (6; -3;1).
Вычислить
а)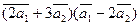 
;
б) .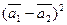
5. Даны векторы (2; -1; 2) и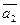 
(3; 1;-1).
Вычислить векторное произведение:
а) ;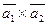
б) .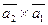
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (3;-5) и В ( 3; 3).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
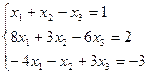
Вариант № 19
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ). Множества
1. Найти матрицу С = 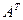– 4В, где А = 
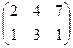; В =
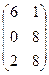
2. Найти решение матричного уравнения АХ=В, имеющего вид:
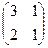Х =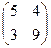 
и сделать проверку.
3. Вычислить:
а) ;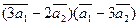
б) ,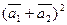
где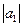 
= 2; 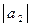= 4; угол между векторами и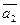
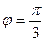
4. Даны векторы (1; 2; -1) и 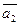(6; -3;1).
Вычислить
а)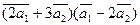 
;
б) .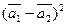
5. Даны векторы 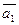(2; -1; 3) и (4; 0;-3).
Вычислить векторное произведение:
а) ;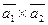
б)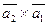 
.
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (3;-2) и В ( -2; 2).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
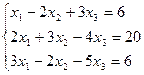
Вариант № 20
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С = А - 4 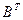, где А = 
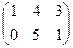; В = 
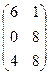
2.Найти решение матричного уравнения АХ=В, имеющего вид:
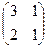Х = 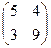и сделать проверку.
3. Вычислить:
а) ;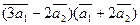
б) ,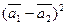
где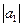 
= 2; 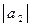= 5; угол между векторами и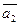 
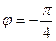
4. Даны векторы 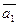(4; 2; -4) и 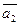(6; -3;2).
Вычислить
а) ;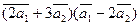
б) .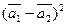
5. Даны векторы (1; -3; 1) и 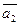(0; 2;-8).
Вычислить векторное произведение:
а)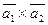 
;
б) .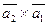
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (-5;-5) и В ( 8; 1).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
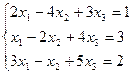
Вариант № 21
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) .
1. Найти матрицу С = 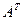- 3В, где А = 
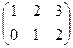; В = 
2. Найти решение матричного уравнения ХА=В, имеющего вид:
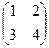Х =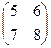 
и сделать проверку.
3. Вычислить:
а) ;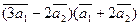
б) ,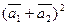
где 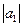= 3; 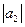= 4; угол между векторами и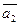
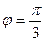
4. Даны векторы (1; 2; -1) и (6; -2;2).
Вычислить
а)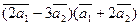 
;
б) .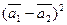
5. Даны векторы 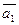(3; -1; 2) и 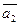(1; 0;-1).
Вычислить векторное произведение:
а) ;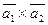
б) .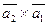
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (5;5) и В ( -1; 6).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
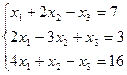
Вариант № 22
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С = 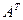- 3В, где А = 
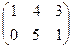; В =
2. Найти решение матричного уравнения XА = В, имеющего вид:
Х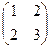 
= 
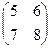и сделать проверку.
3. Вычислить:
а)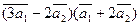 
;
б) ,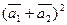
где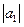 
= 3; 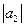= 4; угол между векторам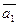и и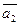
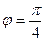
4. Даны векторы (4; 2; -4) и 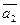(1; -4;2).
Вычислить
а) ;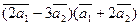
б) .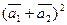
5. Даны векторы (3; -5; 2) и 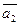(0; 2;-2).
Вычислить векторное произведение:
а)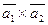 
;
б)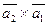 
.
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (5;-8) и В ( 5; 5).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
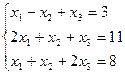
Вариант № 23
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С = А - 4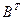 
, где А = 
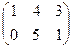; В = 
2.Найти решение матричного уравнения ХА=В, имеющего вид:
Х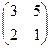 
= 
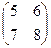и сделать проверку.
3.Вычислить:
а)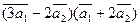 
;
б)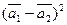 
,
где 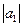= 3; 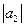= 4; угол между векторам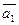и и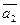 
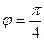
4. Даны векторы (4; 2; -3) и 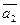(6; -3;0).
Вычислить
а)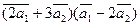 
;
б) .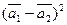
5. Даны векторы 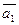(1; -3; 1) и 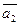(7; 0;-8).
Вычислить векторное произведение:
а) ;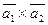
б) .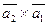
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (2;-4) и В ( 7; 1).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
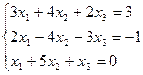
Вариант № 24
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С = А - 4 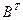, где А = 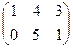; В = 
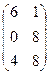
2.Найти решение матричного уравнения АХ=В, имеющего вид:
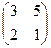Х = 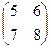и сделать проверку.
3.Вычислить:
а)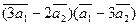 
;
б)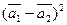 
,
где 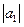= 2; 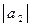= 4; угол между векторам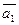и 
и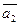 
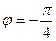
4. Даны векторы 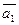(4; 2; -4) и 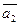(6; -3;0).
Вычислить
а)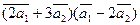 
;
б)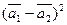 
.
5. Даны векторы 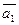(2; -3; 1) и 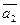(1; 2;-6).
Вычислить векторное произведение:
а) ;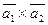
б) .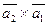
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (-1;-1) и В ( 3; 2).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
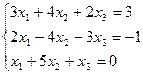
Вариант № 25
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С =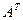 
– 4В, где А = 
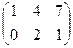; В =
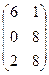
2. Найти решение матричного уравнения АХ=В, имеющего вид:
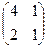Х =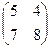 
и сделать проверку.
3. Вычислить:
а)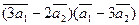 
;
б)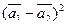 
,
где 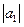= 2;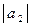 
= 4; угол между векторам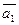и и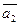 
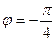
4. Даны векторы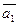 
(1; 2; -1) и 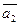(4; -3;1).
Вычислить
а)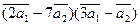 
;
б)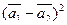 
.
5. Даны векторы 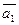(1; -2; 4) и 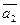(5; -2;3).
Вычислить векторное произведение:
а)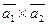 
;
б) .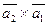
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (3;-4) и В ( 2; 2).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
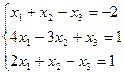
Вариант № 26
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С =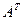 
– 4В, где А = 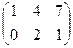; В = 
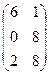
2.Найти решение матричного уравнения АХ=В, имеющего вид:
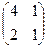Х = 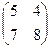и сделать проверку.
3.Вычислить:
а)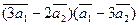 
;
б) ,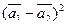
где 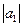= 3; 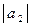= 4; угол между векторам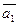и и 
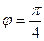
4. Даны векторы 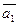(4; 0; -4) и (6; -3;5).
Вычислить
а)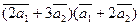 
;
б) .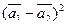
5. Даны векторы 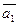(0; -4; 2) и 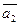(5; 1;-8).
Вычислить векторное произведение:
а) ;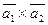
б) .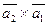
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (8;-3) и В ( 4; 4).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
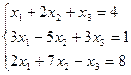
Вариант № 27
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С = 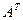– 4В, где А = 
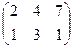; В = 
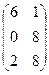
2.Найти решение матричного уравнения АХ=В, имеющего вид:
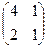Х =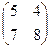 
и сделать проверку.
3.Вычислить:
а)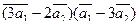 
;
б) ,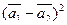
где 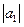= 2; 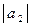= 4; угол между векторам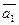и 
и 
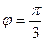
4. Даны векторы 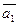(4; 1; -4) и 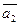(6; -3;1).
Вычислить
а)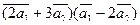 
;
б) .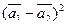
5. Даны векторы 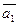(1; -1; 1) и (5; 2;-8).
Вычислить векторное произведение:
а) ;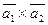
б) .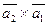
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (-2;-8) и В ( 3; 3).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
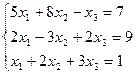
Вариант № 28
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С = 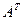– 4В, где А = 
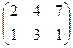; В =
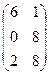
2. Найти решение матричного уравнения АХ=В, имеющего вид:
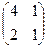Х =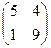 
и сделать проверку.
3.Вычислить:
а)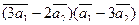 
;
б)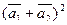 
,
где 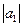= 2; 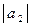= 4; угол между векторам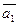и и
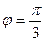
4. Даны векторы 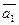(4; 2; -4) и (6; -3;0).
Вычислить
а)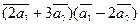 
;
б) .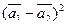
5. Даны векторы 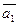(1; -1; 1) и (4; 1;-3).
Вычислить векторное произведение:
а) ;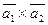
б) .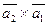
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (3;-2) и В ( 6; 1).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
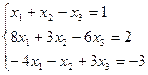
Вариант № 29
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ). Множества
1. Найти матрицу С =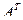 
– 4В, где А = 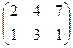; В =
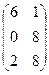
2. Найти решение матричного уравнения АХ=В, имеющего вид:
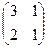Х =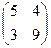 
и сделать проверку.
3. Вычислить:
а) ;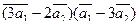
б)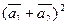 
,
где 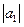= 2; 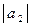= 4; угол между векторам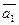и и
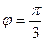
4. Даны векторы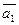 
(4; 2; -4) и (6; -3;0).
Вычислить
а) ;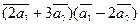
б)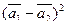 
.
5. Даны векторы 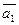(1; -1; 2) и (4; 2;-3).
Вычислить векторное произведение:
а) ;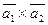
б) .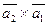
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (3;-7) и В ( -2; 2).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
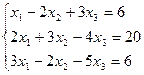
Вариант № 30
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С = А - 4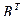 
, где А = 
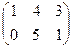; В = 
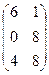
2.Найти решение матричного уравнения АХ=В, имеющего вид:
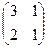Х = 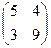и сделать проверку.
3. Вычислить:
а)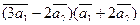 
;
б) ,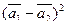
где 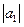= 2;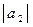 
= 5; угол между векторам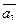и 
и
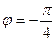
4. Даны векторы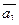 
(4; 1; -4) и (6; -3;-2).
Вычислить
а) ;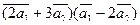
б)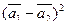 
.
5. Даны векторы 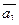(1; -4; 2) и 
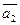(7; 3;-8).
Вычислить векторное произведение:
а) ;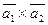
б) .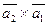
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (-5;-5) и В ( 1; 1).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
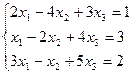
Дата: 2019-07-24, просмотров: 146.
