Министерство Российской Федерации
По делам гражданской обороны, чрезвычайным ситуациям
И ликвидации последствий стихийных бедствий
 Академия гражданской защиты
Академия гражданской защиты
Кафедра системного анализа и управления
Гальченко В. Т., Бахтиярова О.Н.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ПО ИЗУЧЕНИЮ ДИСЦИПЛИНЫ
«ВЫСШАЯ МАТЕМАТИКА»
Химки - 2018
УДК 517.91
ББК 22. 161.6
Г 17
Авторы: Гальченко В. Т., Бахтиярова О.Н,.
Гальченко В.Т. Методические указания по изучению дисциплины « Математика» В.Т. Гальченко, О.Н. Бахтиярова. – Химки: АГЗ МЧС России, 2018 – 88 с.
Настоящие методические указания разработаны в соответствии с учебной программой дисциплины «Математика» и предназначены для студентов заочного факультета , обучающихся по специальности «Пожарная безопасность».
В методических указаниях даны рекомендации по научной организации самостоятельной работы обучающихся при изучении дисциплины, изложены основные цели изучения дисциплины, требования к студентам по её изучению, тематический план и содержание учебных занятий, задания домашней контрольной работы, вопросы для подготовки к экзамену, основная и дополнительная литература для изучения дисциплины.
Компьютерный набор: Гальченко В. Т., Бахтиярова О.Н.
© АГЗ МЧС России, 2018
ВВЕДЕНИЕ
Общей задачей дисциплины является приобретение студентами знаний об основных понятиях и методах высшей математики; формирование современного математического мышления; выработка приемов и навыков решения конкретных задач высшей математики; формирование навыков математического исследования аналитического, численного и прикладного характеров; освоение методов математической формализации различных процессов и явлений; обучению анализу полученных решений.
Главная задача обучения состоит в освоении дисциплины студентами заочного факультета по специальности «Пожарная безопасность» на уровне, позволяющем достаточно квалифицированно выполнять работы в области математического обеспечения, моделирования, прогнозирования и оптимального управления применительно к конкретным задачам инженерной и научной практики поисково-спасательных служб и сил РСЧС.
В результате изучения дисциплины студенты должны:
знать:
_ основные положения теории высшей математики;
. _ . аналитические подходы и математические методы решения базовых
задач;
- математические методы решения прикладных задач и научно
исследовательских задач.
уметь:
- использовать в своей практической деятельности возможности
вычислительной техники, современные математические методы;
- выбирать наиболее подходящие математические методы к анализу
задач, возникающих в практике МЧС.
- формулировать и ставить задачи теоретического и прикладного
характера;
При изучении дисциплины особое внимание уделяется выработке навыков в использовании полученных знаний при решении прикладных задач и научно-исследовательских задач
владеть:
- навыками решения задач по следующим разделам:
а) элементы линейной алгебры;
б) элементы векторной алгебры;
в) аналитической геометрии;
г) пределы и производная функции;
д) исследование функций с помощью производной;
е) комплексные числа и многочлены;
ж) неопределенный интеграл;
з) определенный интеграл;
и) функции многих переменных;
к) кратные и криволинейные интегралы;
математическим аппаратом в исследовательской, расчётно-конструкторской и оперативно-тактической практике специалиста в различных чрезвычайных ситуациях мирного и военного времени.
II. ПЛАН ИЗУЧЕНИЯ ДИСЦИПЛИНЫ ПО ВИДАМ УЧЕБНЫХ ЗАНЯТИЙ
| N п/п | Виды учебных занятий | Количество часов | Тема и учебные вопросы занятия | Материальное обеспечение занятия | Задания на самостоятельную работу | |||||||||
| Литература | Время (в часах) | |||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||||||||
|
| 12 | |||||||||||||
Раздел I Линейная алгебра и аналитическая геометрия
66
Тема № 2 Векторная алгебра.
22
3
Лекция
Занятие 1.
Базис геометрических векторов на прямой, на плоскости и в пространстве. Операции над векторами. Выражение координат вектора через координаты начала и конца. Скалярное произведение их свойства и выражение через координаты.
Маркерная
доска, маркер
11
4
Практическое занятие
Занятие 2.
Векторное и смешанное произведение, их свойства, выражение через координаты. Приложения.
Маркерная
доска, маркер
11
II . СОДЕРЖАНИЕ ДИСЦИПЛИНЫ И ЕЕ РАЗДЕЛОВ
Раздел № 9. Ряды
Тема № 15. Числовые ряды.
Числовые ряды. Сходимость числового ряда. Свойства сходящихся числовых рядов.
Необходимый признак сходимости знакоположительного ряда. Достаточный признак расходимости ряда.
Достаточные признаки сходимости знакоположительных рядов: признак Даламбера, признак Коши, интегральный признак.
Знакопеременные и знакочередующиеся ряды.
Признак Лейбница. Исследование сходимости знакочередующихся рядов.
Тема №16. Степенные ряды.
Степенной ряд, область его сходимости. Свойства степенных рядов
Теорема Абеля.
Интервал и радиус сходимости степенного ряда. Исследование сходимости степенных рядов.
Ряд Тейлора. Остаточный член ряда Тейлора. Ряд Маклорена.
Разложение некоторых элементарных функций в ряды Тейлора и Маклорена.
Ряды Фурье. Разложение функций в ряды Фурье.
IV . ЗАДАНИЯ ДОМАШНЕЙ КОНТРОЛЬНОЙ РАБОТЫ
Примечание. Номер варианта N заданий домашней контрольной работы соответствует номеру по порядку студента в классном журнале учёта успеваемости.
Вариант № 1
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) .
1. Найти матрицу С = 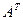 - 3В, где А =
- 3В, где А = 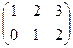 ; В =
; В = 
2. Найти решение матричного уравнения ХА=В, имеющего вид:
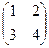 Х =
Х = 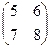 и сделать проверку.
и сделать проверку.
3. Вычислить:
а) 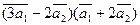 ;
;
б) 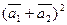 ,
,
где 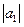 = 3;
= 3; 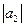 = 4; угол между векторами
= 4; угол между векторами 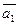 и
и 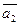
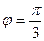
4. Даны векторы 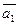 (4; 2; -4) и
(4; 2; -4) и 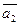 (6; -3;2).
(6; -3;2).
Вычислить
а) 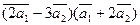 ;
;
б) 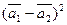 .
.
5. Даны векторы 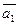 (3; -1; 2) и
(3; -1; 2) и 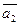 (1; 2;-1).
(1; 2;-1).
Вычислить векторное произведение:
а) 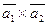 ;
;
б) 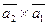 .
.
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (4;5) и В ( -1; 7).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
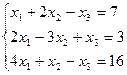
Вариант № 2
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С = 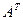 - 3В, где А =
- 3В, где А = 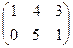 ; В =
; В = 
2. Найти решение матричного уравнения XА = В, имеющего вид:
Х 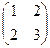 =
= 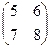 и сделать проверку.
и сделать проверку.
3. Вычислить:
а) 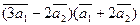 ;
;
б) 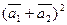 ,
,
где 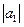 = 3;
= 3; 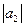 = 4; угол между векторами
= 4; угол между векторами 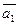 и
и 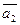
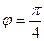
4. Даны векторы 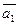 (4; 2; -4) и
(4; 2; -4) и 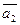 (6; -3;2).
(6; -3;2).
Вычислить
а) 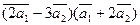 ;
;
б) 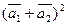 .
.
5. Даны векторы 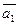 (3; -4; 2) и
(3; -4; 2) и 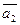 (0; 2;-1).
(0; 2;-1).
Вычислить векторное произведение:
а) 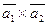 ;
;
б) 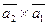 .
.
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (5;-9) и В ( 3; 3).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
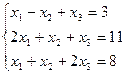
Вариант № 3
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С = А - 4 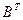 , где А =
, где А = 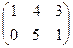 ; В =
; В = 
2.Найти решение матричного уравнения ХА=В, имеющего вид:
Х 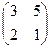 =
= 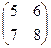 и сделать проверку.
и сделать проверку.
3.Вычислить:
а) 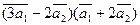 ;
;
б) 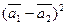 ,
,
где 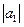 = 3;
= 3; 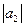 = 4; угол между векторами
= 4; угол между векторами 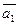 и
и 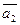
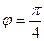
4. Даны векторы 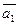 (4; 2; -4) и
(4; 2; -4) и 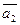 (6; -3;2).
(6; -3;2).
Вычислить
а) 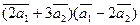 ;
;
б) 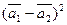 .
.
5. Даны векторы 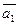 (1; -4; 1) и
(1; -4; 1) и 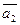 (7; 2;-8).
(7; 2;-8).
Вычислить векторное произведение:
а) 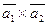 ;
;
б) 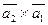 .
.
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (2;-6) и В ( 7; 0).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
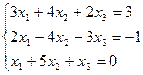
Вариант № 4
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С = А - 4 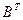 , где А =
, где А = 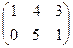 ; В =
; В = 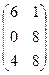
2.Найти решение матричного уравнения АХ=В, имеющего вид:
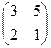 Х =
Х = 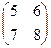 и сделать проверку.
и сделать проверку.
3.Вычислить:
а) 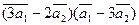 ;
;
б) 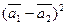 ,
,
где 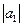 = 2;
= 2; 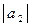 = 4; угол между векторами
= 4; угол между векторами 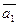 и
и 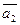
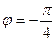
4. Даны векторы 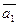 (4; 2; -4) и
(4; 2; -4) и 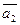 (6; -3;0).
(6; -3;0).
Вычислить
а) 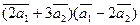 ;
;
б) 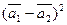 .
.
5. Даны векторы 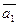 (1; -1; 1) и
(1; -1; 1) и 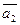 (5; 2;-8).
(5; 2;-8).
Вычислить векторное произведение:
а) 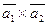 ;
;
б) 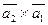 .
.
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (-3;-3) и В ( 1; 2).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
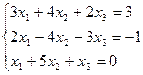
Вариант № 5
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С = 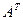 – 4В, где А =
– 4В, где А = 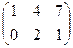 ; В =
; В = 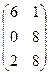
2. Найти решение матричного уравнения АХ=В, имеющего вид:
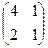 Х =
Х = 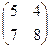 и сделать проверку.
и сделать проверку.
3. Вычислить:
а) 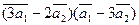 ;
;
б) 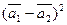 ,
,
где 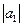 = 2;
= 2; 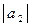 = 4; угол между векторами
= 4; угол между векторами 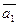 и
и 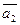
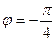
4. Даны векторы 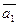 (4; 2; -4) и
(4; 2; -4) и 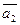 (4; -3;2).
(4; -3;2).
Вычислить
а) 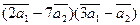 ;
;
б) 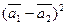 .
.
5. Даны векторы 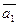 (1; -1; 4) и
(1; -1; 4) и 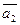 (5; -2;8).
(5; -2;8).
Вычислить векторное произведение:
а) 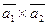 ;
;
б) 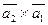 .
.
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (3;-4) и В ( 2; 3).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
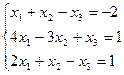
Вариант № 6
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С = 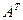 – 4В, где А =
– 4В, где А = 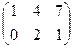 ; В =
; В = 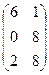
2.Найти решение матричного уравнения АХ=В, имеющего вид:
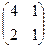 Х =
Х = 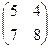 и сделать проверку.
и сделать проверку.
3.Вычислить:
а) 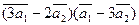 ;
;
б) 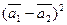 ,
,
где 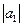 = 3;
= 3; 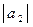 = 4; угол между векторами
= 4; угол между векторами 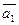 и
и 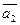
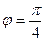
4. Даны векторы 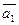 (4; 0; -4) и
(4; 0; -4) и 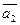 (6; -3;5).
(6; -3;5).
Вычислить
а) 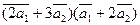 ;
;
б) 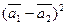 .
.
5. Даны векторы 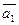 (1; -4; 1) и
(1; -4; 1) и 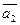 (5; 2;-8).
(5; 2;-8).
Вычислить векторное произведение:
а) 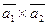 ;
;
б) 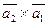 .
.
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (8;-7) и В ( 4; 3).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
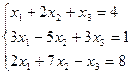
Вариант № 7
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С = 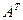 – 4В, где А =
– 4В, где А = 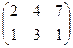 ; В =
; В = 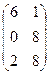
2.Найти решение матричного уравнения АХ=В, имеющего вид:
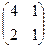 Х =
Х = 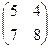 и сделать проверку.
и сделать проверку.
3.Вычислить:
а) 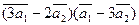 ;
;
б) 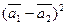 ,
,
где 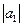 = 2;
= 2; 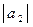 = 4; угол между векторами
= 4; угол между векторами  и
и 
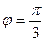
4. Даны векторы  (4; 2; -4) и
(4; 2; -4) и  (6; -3;0).
(6; -3;0).
Вычислить
а) 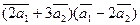 ;
;
б) 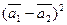 .
.
5. Даны векторы  (1; -1; 1) и
(1; -1; 1) и  (5; 2;-8).
(5; 2;-8).
Вычислить векторное произведение:
а) 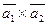 ;
;
б) 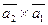 .
.
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (-2;-8) и В ( 5; 3).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
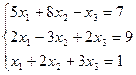
Вариант № 8
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С = 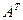 – 4В, где А =
– 4В, где А = 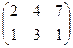 ; В =
; В = 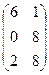
2. Найти решение матричного уравнения АХ=В, имеющего вид:
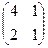 Х =
Х = 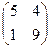 и сделать проверку.
и сделать проверку.
3.Вычислить:
а) 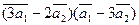 ;
;
б) 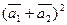 ,
,
где 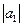 = 2;
= 2; 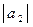 = 4; угол между векторами
= 4; угол между векторами  и
и 
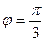
4. Даны векторы  (4; 2; -4) и
(4; 2; -4) и  (6; -3;0).
(6; -3;0).
Вычислить
а) 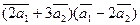 ;
;
б) 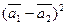 .
.
5. Даны векторы  (1; -1; 1) и
(1; -1; 1) и  (4; 1;-3).
(4; 1;-3).
Вычислить векторное произведение:
а) 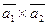 ;
;
б) 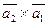 .
.
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (3;-6) и В ( 6; 3).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
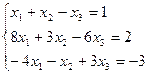
Вариант № 9
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ). Множества
1. Найти матрицу С = 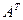 – 4В, где А =
– 4В, где А = 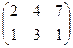 ; В =
; В = 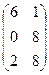
2. Найти решение матричного уравнения АХ=В, имеющего вид:
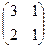 Х =
Х = 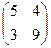 и сделать проверку.
и сделать проверку.
3. Вычислить:
а) 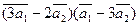 ;
;
б) 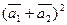 ,
,
где 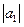 = 2;
= 2; 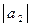 = 4; угол между векторами
= 4; угол между векторами  и
и 
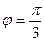
4. Даны векторы  (4; 2; -4) и
(4; 2; -4) и  (6; -3;0).
(6; -3;0).
Вычислить
а) 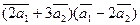 ;
;
б) 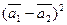 .
.
5. Даны векторы  (1; -1; 1) и
(1; -1; 1) и  (4; 1;-3).
(4; 1;-3).
Вычислить векторное произведение:
а) 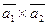 ;
;
б) 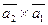 .
.
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (3;-8) и В ( -2; 3).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
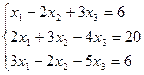
Вариант № 10
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С = А - 4 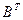 , где А =
, где А = 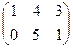 ; В =
; В = 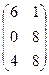
2.Найти решение матричного уравнения АХ=В, имеющего вид:
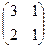 Х =
Х = 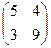 и сделать проверку.
и сделать проверку.
3. Вычислить:
а) 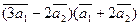 ;
;
б) 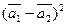 ,
,
где 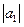 = 2;
= 2; 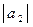 = 5; угол между векторами
= 5; угол между векторами  и
и 
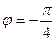
4. Даны векторы  (4; 2; -4) и
(4; 2; -4) и  (6; -3;2).
(6; -3;2).
Вычислить
а) 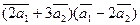 ;
;
б) 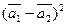 .
.
5. Даны векторы  (1; -4; 1) и
(1; -4; 1) и  (7; 2;-8).
(7; 2;-8).
Вычислить векторное произведение:
а) 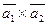 ;
;
б) 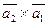 .
.
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (-5;-5) и В ( 8; 1).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
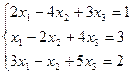
Вариант № 11
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) .
1. Найти матрицу С = 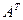 - 3В, где А =
- 3В, где А = 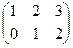 ; В =
; В = 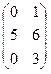
2. Найти решение матричного уравнения ХА=В, имеющего вид:
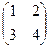 Х =
Х = 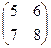 и сделать проверку.
и сделать проверку.
3. Вычислить:
а) 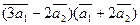 ;
;
б) 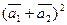 ,
,
где 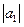 = 4;
= 4; 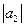 = 4; угол между векторами
= 4; угол между векторами  и
и 
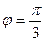
4. Даны векторы  (5; 2; -5) и
(5; 2; -5) и  (3; -3;2).
(3; -3;2).
Вычислить
а) 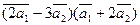 ;
;
б) 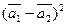 .
.
5. Даны векторы  (0; -1; -2) и
(0; -1; -2) и  (1; 2;-4).
(1; 2;-4).
Вычислить векторное произведение:
а) 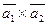 ;
;
б) 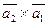 .
.
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (4;3) и В ( -1; 1).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
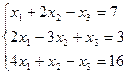
Вариант № 12
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С = 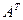 - 3В, где А =
- 3В, где А = 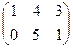 ; В =
; В = 
2. Найти решение матричного уравнения XА = В, имеющего вид:
Х 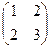 =
= 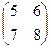 и сделать проверку.
и сделать проверку.
3. Вычислить:
а) 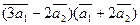 ;
;
б) 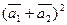 ,
,
где 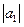 = 5;
= 5; 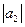 = 4; угол между векторами
= 4; угол между векторами  и
и 
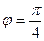
4. Даны векторы  (3; 2; -3) и
(3; 2; -3) и  (2; -3;2).
(2; -3;2).
Вычислить
а) 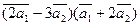 ;
;
б) 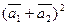 .
.
5. Даны векторы  (3; 0; 2) и
(3; 0; 2) и  (0; 2;-2).
(0; 2;-2).
Вычислить векторное произведение:
а) 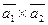 ;
;
б) 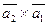 .
.
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (3;-4) и В ( 3; 3).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
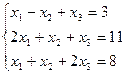
Вариант №1 3
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С = А - 4 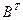 , где А =
, где А = 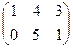 ; В =
; В = 
2.Найти решение матричного уравнения ХА=В, имеющего вид:
Х 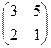 =
= 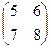 и сделать проверку.
и сделать проверку.
3.Вычислить:
а) 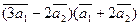 ;
;
б) 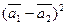 ,
,
где 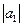 = 2;
= 2; 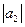 = 4; угол между векторами
= 4; угол между векторами  и
и 
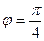
4. Даны векторы  (5; 2; -1) и
(5; 2; -1) и  (6; -1;2).
(6; -1;2).
Вычислить
а) 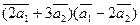 ;
;
б) 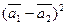 .
.
5. Даны векторы  (1; -4; 1) и
(1; -4; 1) и  (6; -2;-1).
(6; -2;-1).
Вычислить векторное произведение:
а) 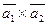 ;
;
б) 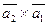 .
.
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (2;-2) и В ( 5; 0).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
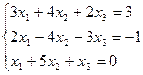
Вариант № 1 4
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С = А - 4 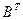 , где А =
, где А = 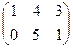 ; В =
; В = 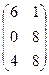
2.Найти решение матричного уравнения АХ=В, имеющего вид:
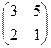 Х =
Х = 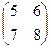 и сделать проверку.
и сделать проверку.
3.Вычислить:
а) 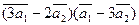 ;
;
б) 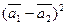 ,
,
где 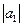 = 1;
= 1; 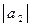 = 4; угол между векторами
= 4; угол между векторами  и
и 
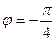
4. Даны векторы  (4; 2; -4) и
(4; 2; -4) и 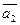 (6; -3;1).
(6; -3;1).
Вычислить
а) 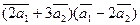 ;
;
б) 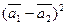 .
.
5. Даны векторы  (2; -1; 2) и
(2; -1; 2) и  (5; 2;-0).
(5; 2;-0).
Вычислить векторное произведение:
а) 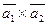 ;
;
б) 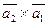 .
.
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (-3;-1) и В ( 2; 2).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
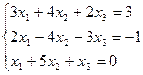
Вариант № 1 5
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С = 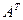 – 4В, где А =
– 4В, где А = 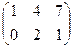 ; В =
; В = 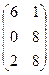
2. Найти решение матричного уравнения АХ=В, имеющего вид:
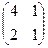 Х =
Х = 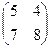 и сделать проверку.
и сделать проверку.
3. Вычислить:
а) 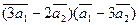 ;
;
б) 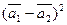 ,
,
где 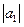 = 1;
= 1; 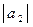 = 6; угол между векторами
= 6; угол между векторами 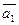 и
и 
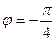
4. Даны векторы  (3; 2; -3) и
(3; 2; -3) и 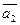 (1; -3;1).
(1; -3;1).
Вычислить
а) 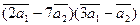 ;
;
б) 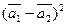 .
.
5. Даны векторы  (1; -1; 2) и
(1; -1; 2) и 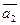 (5; -3;8).
(5; -3;8).
Вычислить векторное произведение:
а) 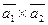 ;
;
б) 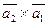 .
.
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (3;-2) и В ( 2; -3).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
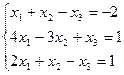
Вариант № 16
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С = 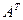 – 4В, где А =
– 4В, где А = 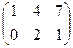 ; В =
; В = 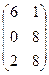
2.Найти решение матричного уравнения АХ=В, имеющего вид:
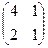 Х =
Х = 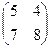 и сделать проверку.
и сделать проверку.
3.Вычислить:
а) 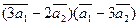 ;
;
б) 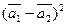 ,
,
где 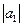 = 3;
= 3; 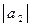 = 4; угол между векторами
= 4; угол между векторами  и
и 
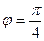
4. Даны векторы  (2; 1; -2) и
(2; 1; -2) и  (5; -3;5).
(5; -3;5).
Вычислить
а) 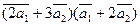 ;
;
б) 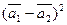 .
.
5. Даны векторы  (1; -1; 1) и
(1; -1; 1) и 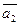 (5; 2;-0).
(5; 2;-0).
Вычислить векторное произведение:
а) 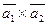 ;
;
б) 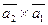 .
.
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (8;-7) и В ( 4; 3).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
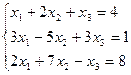
Вариант № 17
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С = 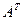 – 4В, где А =
– 4В, где А = 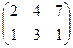 ; В =
; В = 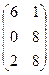
2.Найти решение матричного уравнения АХ=В, имеющего вид:
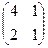 Х =
Х = 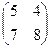 и сделать проверку.
и сделать проверку.
3.Вычислить:
а) 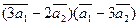 ;
;
б) 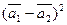 ,
,
где 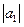 = 2;
= 2; 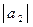 = 4; угол между векторами
= 4; угол между векторами 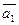 и
и 
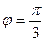
4. Даны векторы 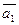 (4; 2; -2) и
(4; 2; -2) и  (6; -3;1).
(6; -3;1).
Вычислить
а) 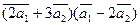 ;
;
б) 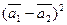 .
.
5. Даны векторы  (1; -2; 1) и
(1; -2; 1) и  (5; 0;-8).
(5; 0;-8).
Вычислить векторное произведение:
а) 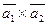 ;
;
б) 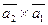 .
.
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (-2;-2) и В ( 5; 3).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
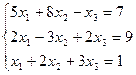
Вариант № 18
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С = 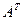 – 4В, где А =
– 4В, где А = 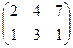 ; В =
; В = 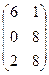
2. Найти решение матричного уравнения АХ=В, имеющего вид:
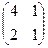 Х =
Х = 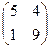 и сделать проверку.
и сделать проверку.
3.Вычислить:
а) 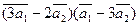 ;
;
б) 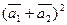 ,
,
где 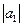 = 2;
= 2; 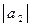 = 4; угол между векторами
= 4; угол между векторами  и
и 
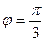
4. Даны векторы  (1; 2; -1) и
(1; 2; -1) и  (6; -3;1).
(6; -3;1).
Вычислить
а) 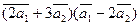 ;
;
б) 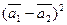 .
.
5. Даны векторы  (2; -1; 2) и
(2; -1; 2) и 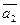 (3; 1;-1).
(3; 1;-1).
Вычислить векторное произведение:
а) 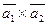 ;
;
б) 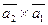 .
.
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (3;-5) и В ( 3; 3).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
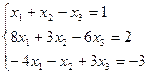
Вариант № 19
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ). Множества
1. Найти матрицу С = 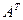 – 4В, где А =
– 4В, где А = 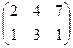 ; В =
; В = 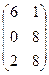
2. Найти решение матричного уравнения АХ=В, имеющего вид:
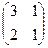 Х =
Х = 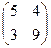 и сделать проверку.
и сделать проверку.
3. Вычислить:
а) 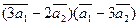 ;
;
б) 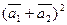 ,
,
где 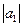 = 2;
= 2; 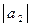 = 4; угол между векторами
= 4; угол между векторами  и
и 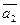
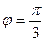
4. Даны векторы  (1; 2; -1) и
(1; 2; -1) и 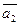 (6; -3;1).
(6; -3;1).
Вычислить
а) 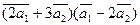 ;
;
б) 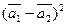 .
.
5. Даны векторы 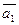 (2; -1; 3) и
(2; -1; 3) и  (4; 0;-3).
(4; 0;-3).
Вычислить векторное произведение:
а) 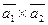 ;
;
б) 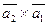 .
.
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (3;-2) и В ( -2; 2).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
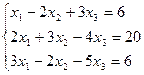
Вариант № 20
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С = А - 4 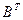 , где А =
, где А = 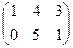 ; В =
; В = 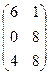
2.Найти решение матричного уравнения АХ=В, имеющего вид:
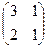 Х =
Х = 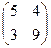 и сделать проверку.
и сделать проверку.
3. Вычислить:
а) 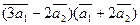 ;
;
б) 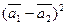 ,
,
где 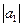 = 2;
= 2; 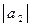 = 5; угол между векторами
= 5; угол между векторами  и
и 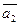
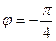
4. Даны векторы 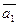 (4; 2; -4) и
(4; 2; -4) и 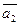 (6; -3;2).
(6; -3;2).
Вычислить
а) 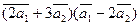 ;
;
б) 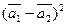 .
.
5. Даны векторы  (1; -3; 1) и
(1; -3; 1) и 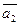 (0; 2;-8).
(0; 2;-8).
Вычислить векторное произведение:
а) 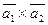 ;
;
б) 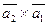 .
.
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (-5;-5) и В ( 8; 1).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
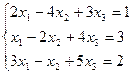
Вариант № 21
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) .
1. Найти матрицу С = 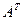 - 3В, где А =
- 3В, где А = 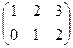 ; В =
; В = 
2. Найти решение матричного уравнения ХА=В, имеющего вид:
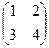 Х =
Х = 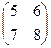 и сделать проверку.
и сделать проверку.
3. Вычислить:
а) 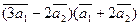 ;
;
б) 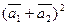 ,
,
где 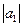 = 3;
= 3; 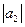 = 4; угол между векторами
= 4; угол между векторами  и
и 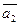
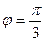
4. Даны векторы  (1; 2; -1) и
(1; 2; -1) и  (6; -2;2).
(6; -2;2).
Вычислить
а) 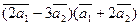 ;
;
б) 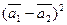 .
.
5. Даны векторы 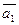 (3; -1; 2) и
(3; -1; 2) и 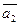 (1; 0;-1).
(1; 0;-1).
Вычислить векторное произведение:
а) 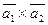 ;
;
б) 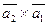 .
.
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (5;5) и В ( -1; 6).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
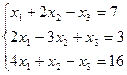
Вариант № 22
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С = 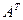 - 3В, где А =
- 3В, где А = 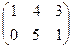 ; В =
; В = 
2. Найти решение матричного уравнения XА = В, имеющего вид:
Х 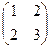 =
= 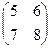 и сделать проверку.
и сделать проверку.
3. Вычислить:
а) 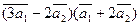 ;
;
б) 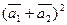 ,
,
где 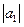 = 3;
= 3; 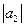 = 4; угол между векторами
= 4; угол между векторами 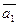 и
и 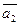
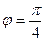
4. Даны векторы  (4; 2; -4) и
(4; 2; -4) и 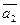 (1; -4;2).
(1; -4;2).
Вычислить
а) 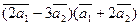 ;
;
б) 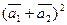 .
.
5. Даны векторы  (3; -5; 2) и
(3; -5; 2) и 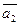 (0; 2;-2).
(0; 2;-2).
Вычислить векторное произведение:
а) 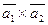 ;
;
б) 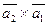 .
.
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (5;-8) и В ( 5; 5).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
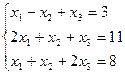
Вариант № 23
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С = А - 4 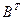 , где А =
, где А = 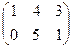 ; В =
; В = 
2.Найти решение матричного уравнения ХА=В, имеющего вид:
Х 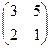 =
= 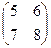 и сделать проверку.
и сделать проверку.
3.Вычислить:
а) 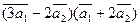 ;
;
б) 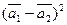 ,
,
где 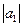 = 3;
= 3; 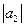 = 4; угол между векторами
= 4; угол между векторами 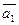 и
и 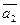
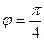
4. Даны векторы  (4; 2; -3) и
(4; 2; -3) и 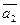 (6; -3;0).
(6; -3;0).
Вычислить
а) 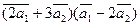 ;
;
б) 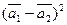 .
.
5. Даны векторы 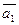 (1; -3; 1) и
(1; -3; 1) и 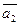 (7; 0;-8).
(7; 0;-8).
Вычислить векторное произведение:
а) 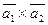 ;
;
б) 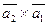 .
.
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (2;-4) и В ( 7; 1).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
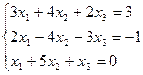
Вариант № 24
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С = А - 4 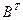 , где А =
, где А = 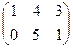 ; В =
; В = 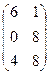
2.Найти решение матричного уравнения АХ=В, имеющего вид:
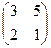 Х =
Х = 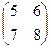 и сделать проверку.
и сделать проверку.
3.Вычислить:
а) 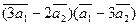 ;
;
б) 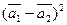 ,
,
где 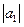 = 2;
= 2; 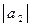 = 4; угол между векторами
= 4; угол между векторами 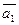 и
и 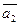
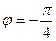
4. Даны векторы 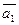 (4; 2; -4) и
(4; 2; -4) и 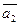 (6; -3;0).
(6; -3;0).
Вычислить
а) 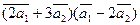 ;
;
б) 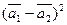 .
.
5. Даны векторы 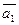 (2; -3; 1) и
(2; -3; 1) и 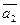 (1; 2;-6).
(1; 2;-6).
Вычислить векторное произведение:
а) 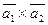 ;
;
б) 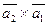 .
.
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (-1;-1) и В ( 3; 2).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
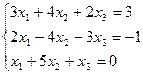
Вариант № 25
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С = 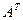 – 4В, где А =
– 4В, где А = 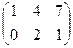 ; В =
; В = 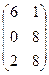
2. Найти решение матричного уравнения АХ=В, имеющего вид:
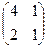 Х =
Х = 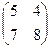 и сделать проверку.
и сделать проверку.
3. Вычислить:
а) 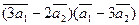 ;
;
б) 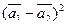 ,
,
где 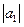 = 2;
= 2; 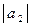 = 4; угол между векторами
= 4; угол между векторами 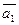 и
и 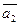
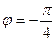
4. Даны векторы 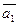 (1; 2; -1) и
(1; 2; -1) и 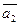 (4; -3;1).
(4; -3;1).
Вычислить
а) 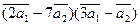 ;
;
б) 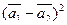 .
.
5. Даны векторы 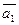 (1; -2; 4) и
(1; -2; 4) и 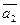 (5; -2;3).
(5; -2;3).
Вычислить векторное произведение:
а) 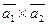 ;
;
б) 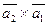 .
.
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (3;-4) и В ( 2; 2).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
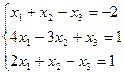
Вариант № 26
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С = 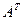 – 4В, где А =
– 4В, где А = 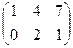 ; В =
; В = 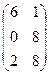
2.Найти решение матричного уравнения АХ=В, имеющего вид:
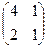 Х =
Х = 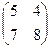 и сделать проверку.
и сделать проверку.
3.Вычислить:
а) 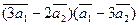 ;
;
б) 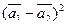 ,
,
где 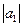 = 3;
= 3; 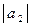 = 4; угол между векторами
= 4; угол между векторами 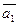 и
и 
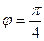
4. Даны векторы 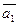 (4; 0; -4) и
(4; 0; -4) и  (6; -3;5).
(6; -3;5).
Вычислить
а) 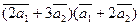 ;
;
б) 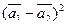 .
.
5. Даны векторы 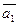 (0; -4; 2) и
(0; -4; 2) и 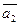 (5; 1;-8).
(5; 1;-8).
Вычислить векторное произведение:
а) 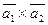 ;
;
б) 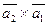 .
.
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (8;-3) и В ( 4; 4).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
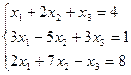
Вариант № 27
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С = 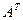 – 4В, где А =
– 4В, где А = 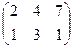 ; В =
; В = 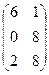
2.Найти решение матричного уравнения АХ=В, имеющего вид:
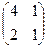 Х =
Х = 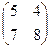 и сделать проверку.
и сделать проверку.
3.Вычислить:
а) 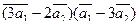 ;
;
б) 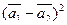 ,
,
где 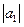 = 2;
= 2; 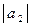 = 4; угол между векторами
= 4; угол между векторами 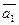 и
и 
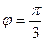
4. Даны векторы 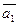 (4; 1; -4) и
(4; 1; -4) и 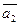 (6; -3;1).
(6; -3;1).
Вычислить
а) 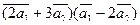 ;
;
б) 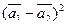 .
.
5. Даны векторы 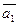 (1; -1; 1) и
(1; -1; 1) и  (5; 2;-8).
(5; 2;-8).
Вычислить векторное произведение:
а) 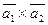 ;
;
б) 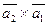 .
.
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (-2;-8) и В ( 3; 3).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
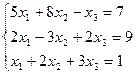
Вариант № 28
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С = 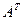 – 4В, где А =
– 4В, где А = 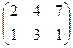 ; В =
; В = 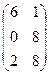
2. Найти решение матричного уравнения АХ=В, имеющего вид:
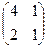 Х =
Х = 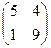 и сделать проверку.
и сделать проверку.
3.Вычислить:
а) 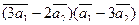 ;
;
б) 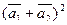 ,
,
где 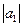 = 2;
= 2; 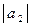 = 4; угол между векторами
= 4; угол между векторами 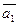 и
и 
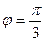
4. Даны векторы 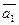 (4; 2; -4) и
(4; 2; -4) и  (6; -3;0).
(6; -3;0).
Вычислить
а) 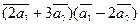 ;
;
б) 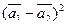 .
.
5. Даны векторы 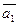 (1; -1; 1) и
(1; -1; 1) и  (4; 1;-3).
(4; 1;-3).
Вычислить векторное произведение:
а) 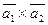 ;
;
б) 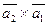 .
.
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (3;-2) и В ( 6; 1).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
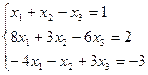
Вариант № 29
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ). Множества
1. Найти матрицу С = 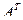 – 4В, где А =
– 4В, где А = 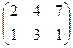 ; В =
; В = 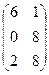
2. Найти решение матричного уравнения АХ=В, имеющего вид:
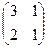 Х =
Х = 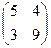 и сделать проверку.
и сделать проверку.
3. Вычислить:
а) 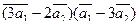 ;
;
б) 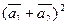 ,
,
где 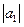 = 2;
= 2; 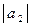 = 4; угол между векторами
= 4; угол между векторами 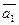 и
и 
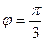
4. Даны векторы 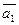 (4; 2; -4) и
(4; 2; -4) и  (6; -3;0).
(6; -3;0).
Вычислить
а) 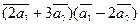 ;
;
б) 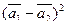 .
.
5. Даны векторы 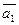 (1; -1; 2) и
(1; -1; 2) и  (4; 2;-3).
(4; 2;-3).
Вычислить векторное произведение:
а) 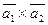 ;
;
б) 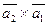 .
.
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (3;-7) и В ( -2; 2).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
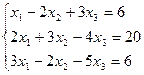
Вариант № 30
Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ) ).
1. Найти матрицу С = А - 4 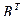 , где А =
, где А = 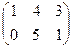 ; В =
; В = 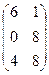
2.Найти решение матричного уравнения АХ=В, имеющего вид:
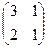 Х =
Х = 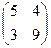 и сделать проверку.
и сделать проверку.
3. Вычислить:
а) 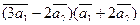 ;
;
б) 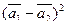 ,
,
где 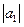 = 2;
= 2; 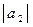 = 5; угол между векторами
= 5; угол между векторами 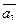 и
и 
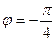
4. Даны векторы 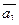 (4; 1; -4) и
(4; 1; -4) и  (6; -3;-2).
(6; -3;-2).
Вычислить
а) 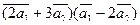 ;
;
б) 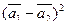 .
.
5. Даны векторы 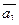 (1; -4; 2) и
(1; -4; 2) и 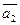 (7; 3;-8).
(7; 3;-8).
Вычислить векторное произведение:
а) 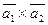 ;
;
б) 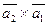 .
.
в) найти модуль векторного произведения
6. Составить и построить уравнения прямой, проходящей через две точки А (-5;-5) и В ( 1; 1).
7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.
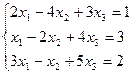
Вариант № 1
1. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.
1) 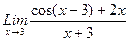 , 2)
, 2) 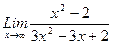 , 3)
, 3) 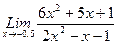 .
.
2. Найти производные первого порядка данных функций, используя правила вычисления производных 
1) 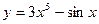 , 2)
, 2) 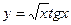 , 3)
, 3) 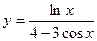 ,
,
4) 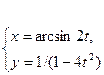 .
.
3. Построить график функции y = f(x), используя схему исследования функции
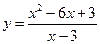 .
.
Вариант № 2
1. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.
1) 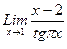 , 2)
, 2) 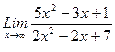 , 3)
, 3) 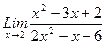 .
.
2. Найти производные первого порядка данных функций, используя правила вычисления производных 
1) 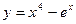 , 2)
, 2) 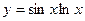 , 3)
, 3) 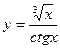 ,
,
4) 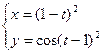
3. Построить график функции y = f(x), используя схему исследования функции
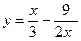 .
.
Вариант № 3
1. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.
1) 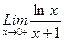 , 2)
, 2) 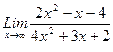 , 3)
, 3) 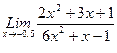 .
.
2. Найти производные первого порядка данных функций, используя правила вычисления производных 
1) 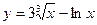 , 2)
, 2) 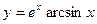 , 3)
, 3) 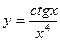 ,
,
4) 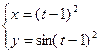 .
.
3. Построить график функции y=f(x), используя схему исследования функции
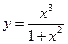 .
.
Вариант № 4
1. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.
1) 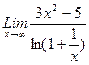 , 2)
, 2) 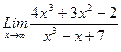 , 3)
, 3) 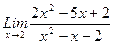 .
.
2. Найти производные первого порядка данных функций, используя правила вычисления производных 
1) 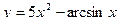 , 2)
, 2) 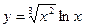 , 3)
, 3) 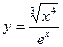 , 4)
, 4) 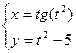 .
.
3. Построить график функции y = f(x), используя схему исследования функции
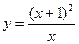 .
.
Вариант № 5
1. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.
1) 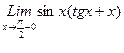 , 2)
, 2) 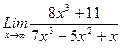 , 3)
, 3) 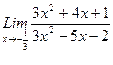 .
.
2. Найти производные первого порядка данных функций, используя правила вычисления производных 
1) 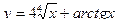 , 2)
, 2) 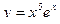 , 3)
, 3) 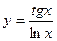 , 4)
, 4) 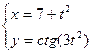 .
.
3. Построить график функции y=f(x), используя схему исследования функции
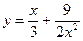 .
.
Вариант № 6
1. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.
1) 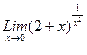 , 2)
, 2) 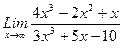 , 3)
, 3) 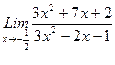 .
.
2. Найти производные первого порядка данных функций, используя правила вычисления производных 
1) 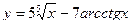 , 2)
, 2) 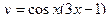 , 3)
, 3) 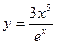 , 4)
, 4) 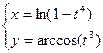 .
.
3. Построить график функции y = f(x), используя схему исследования функции
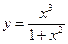 .
.
Вариант № 7
1. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.
1) 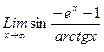 , 2)
, 2) 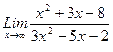 , 3)
, 3) 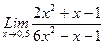 .
.
2. Найти производные первого порядка данных функций, используя правила вычисления производных 
1) 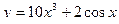 , 2)
, 2) 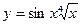 , 3)
, 3) 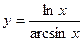 , 4)
, 4) 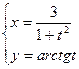 .
.
3. Построить график функции y = f(x), используя схему исследования функции
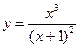 .
.
Вариант № 8
1. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.
1) 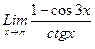 , 2)
, 2) 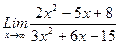 , 3)
, 3) 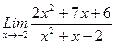 .
.
2. Найти производные первого порядка данных функций, используя правила вычисления производных 
1) 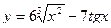 , 2)
, 2) 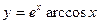 , 3)
, 3) 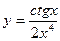 , 4)
, 4) 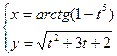 .
.
3. Построить график функции y=f(x), используя схему исследования функции
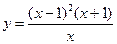 .
.
Вариант № 9
1. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.
1) 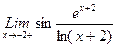 , 2)
, 2) 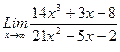 , 3)
, 3) 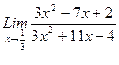 .
.
2. Найти производные первого порядка данных функций, используя правила вычисления производных 
1) 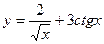 ,
, 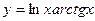 ,
, 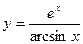 ,
, 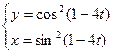 .
.
3. Построить график функции y=f(x), используя схему исследования функции
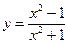 .
.
Вариант № 10
1. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.
1) 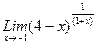 , 2)
, 2) 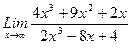 , 3)
, 3) 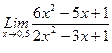 .
.
2. Найти производные первого порядка данных функций, используя правила вычисления производных 
1) 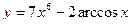 , 2)
, 2) 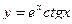 , 3)
, 3) 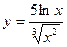 , 4)
, 4) 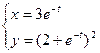 .
.
3. Построить график функции y=f(x), используя схему исследования функции
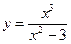 .
.
Вариант № 11
1. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.
1) 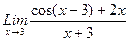 , 2)
, 2) 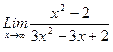 , 3)
, 3) 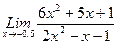 .
.
2. Найти производные первого порядка данных функций, используя правила вычисления производных 
2) 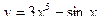 , 2)
, 2) 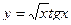 , 3)
, 3) 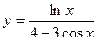 ,
,
4) 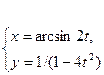 .
.
3. Построить график функции y=f(x), используя схему исследования функции
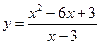 .
.
Вариант № 12.
1. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.
1) 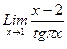 , 2)
, 2) 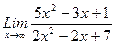 , 3)
, 3) 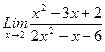 .
.
2. Найти производные первого порядка данных функций, используя правила вычисления производных 
2) 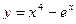 , 2)
, 2) 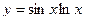 , 3)
, 3) 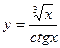 ,
,
4) 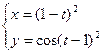
3. Построить график функции y=f(x), используя схему исследования функции
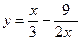 .
.
Вариант № 13
1. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.
1) 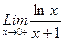 , 2)
, 2) 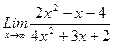 , 3)
, 3) 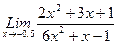 .
.
2. Найти производные первого порядка данных функций, используя правила вычисления производных 
2) 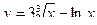 , 2)
, 2) 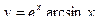 , 3)
, 3) 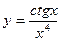 ,
,
4) 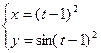 .
.
3. Построить график функции y = f(x), используя схему исследования функции
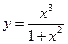 .
.
Вариант № 14
1. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.
1) 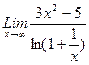 , 2)
, 2) 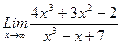 , 3)
, 3) 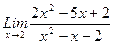 .
.
2. Найти производные первого порядка данных функций, используя правила вычисления производных 
1) 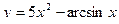 , 2)
, 2) 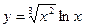 , 3)
, 3) 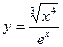 , 4)
, 4) 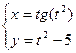 .
.
3. Построить график функции y = f(x), используя схему исследования функции
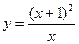 .
.
Вариант № 15
1. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.
1) 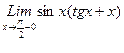 , 2)
, 2) 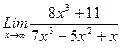 , 3)
, 3) 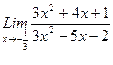 .
.
2. Найти производные первого порядка данных функций, используя правила вычисления производных 
1) 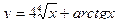 , 2)
, 2) 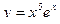 , 3)
, 3) 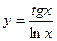 , 4)
, 4) 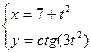 .
.
3. Построить график функции y = f(x), используя схему исследования функции
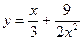 .
.
Вариант № 16
1. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.
1) 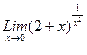 , 2)
, 2) 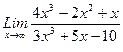 , 3)
, 3) 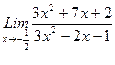 .
.
2. Найти производные первого порядка данных функций, используя правила вычисления производных 
1) 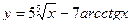 , 2)
, 2) 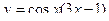 , 3)
, 3) 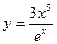 , 4)
, 4) 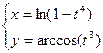 .
.
3. Построить график функции y = f(x), используя схему исследования функции
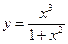 .
.
Вариант № 17
1. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.
1) 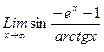 , 2)
, 2) 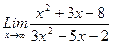 , 3)
, 3) 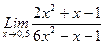 .
.
2. Найти производные первого порядка данных функций, используя правила вычисления производных 
1) 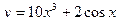 , 2)
, 2) 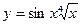 , 3)
, 3) 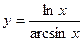 , 4)
, 4) 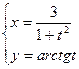 .
.
3. Построить график функции y = f(x), используя схему исследования функции
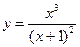 .
.
Вариант № 18
1. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.
1) 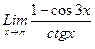 , 2)
, 2) 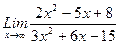 , 3)
, 3) 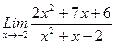 .
.
2. Найти производные первого порядка данных функций, используя правила вычисления производных 
1) 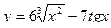 , 2)
, 2) 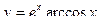 , 3)
, 3) 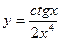 , 4)
, 4) 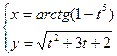 .
.
3. Построить график функции y=f(x), используя схему исследования функции
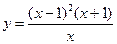 .
.
Вариант № 19
1. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.
1) 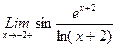 , 2)
, 2) 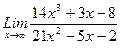 , 3)
, 3) 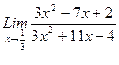 .
.
2. Найти производные первого порядка данных функций, используя правила вычисления производных 
1) 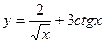 ,
, 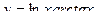 ,
, 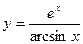 ,
,  .
.
3. Построить график функции y = f(x), используя схему исследования функции
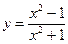 .
.
Вариант № 20
1. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.
1) 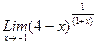 , 2)
, 2) 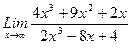 , 3)
, 3) 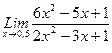 .
.
2. Найти производные первого порядка данных функций, используя правила вычисления производных 
1) 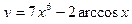 , 2)
, 2) 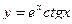 , 3)
, 3) 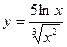 , 4)
, 4) 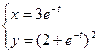 .
.
3. Построить график функции y = f(x), используя схему исследования функции
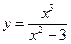 .
.
Вариант № 21
1. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.
1) 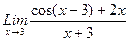 , 2)
, 2) 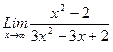 , 3)
, 3) 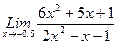 .
.
2. Найти производные первого порядка данных функций, используя правила вычисления производных 
3) 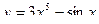 , 2)
, 2) 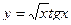 , 3)
, 3) 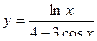 ,
,
4) 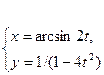 .
.
3. Построить график функции y = f(x), используя схему исследования функции
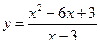 .
.
Вариант № 22
1. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.
1) 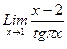 , 2)
, 2) 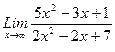 , 3)
, 3) 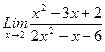 .
.
2. Найти производные первого порядка данных функций, используя правила вычисления производных 
3) 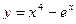 , 2)
, 2) 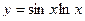 , 3)
, 3) 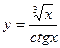 ,
,
4) 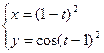
3. Построить график функции y=f(x), используя схему исследования функции
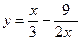 .
.
Вариант №23
1. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.
1) 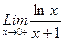 , 2)
, 2) 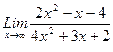 , 3)
, 3) 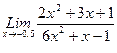 .
.
2. Найти производные первого порядка данных функций, используя правила вычисления производных 
3) 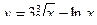 , 2)
, 2) 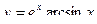 , 3)
, 3) 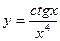 ,
,
4) 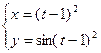 .
.
3. Построить график функции y = f(x), используя схему исследования функции
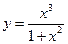 .
.
Вариант № 24
1. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.
1) 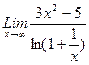 , 2)
, 2) 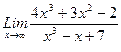 , 3)
, 3) 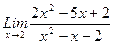 .
.
2. Найти производные первого порядка данных функций, используя правила вычисления производных 
1) 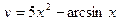 , 2)
, 2) 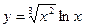 , 3)
, 3) 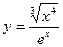 , 4)
, 4) 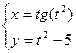 .
.
3. Построить график функции y=f(x), используя схему исследования функции
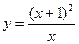 .
.
Вариант №2 5
1. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.
1) 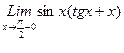 , 2)
, 2) 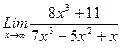 , 3)
, 3) 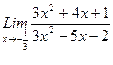 .
.
2. Найти производные первого порядка данных функций, используя правила вычисления производных 
1) 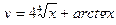 , 2)
, 2) 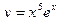 , 3)
, 3) 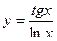 , 4)
, 4) 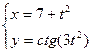 .
.
3. Построить график функции y = f(x), используя схему исследования функции
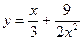 .
.
Вариант № 26
1. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.
1) 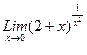 , 2)
, 2) 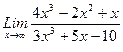 , 3)
, 3) 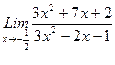 .
.
2. Найти производные первого порядка данных функций, используя правила вычисления производных 
1) 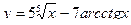 , 2)
, 2) 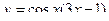 , 3)
, 3) 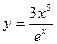 , 4)
, 4) 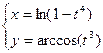 .
.
3. Построить график функции y=f(x), используя схему исследования функции
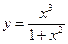 .
.
Вариант № 27
1. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.
1) 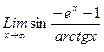 , 2)
, 2) 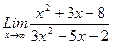 , 3)
, 3) 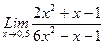 .
.
2. Найти производные первого порядка данных функций, используя правила вычисления производных 
1) 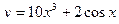 , 2)
, 2) 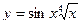 , 3)
, 3) 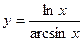 , 4)
, 4) 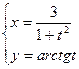 .
.
3. Построить график функции y = f(x), используя схему исследования функции
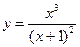 .
.
Вариант № 28
1. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.
1) 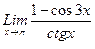 , 2)
, 2) 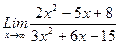 , 3)
, 3) 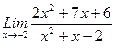 .
.
2. Найти производные первого порядка данных функций, используя правила вычисления производных 
1) 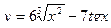 , 2)
, 2) 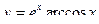 , 3)
, 3) 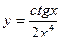 , 4)
, 4) 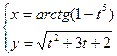 .
.
3. Построить график функции y=f(x), используя схему исследования функции
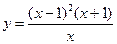 .
.
Вариант № 29
1. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.
1) 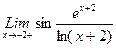 , 2)
, 2) 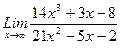 , 3)
, 3) 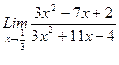 .
.
2. Найти производные первого порядка данных функций, используя правила вычисления производных 
1) 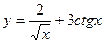 ,
, 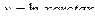 ,
, 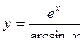 ,
, 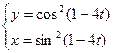 .
.
3. Построить график функции y = f(x), используя схему исследования функции
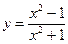 .
.
Вариант № 30
1. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.
1) 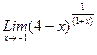 , 2)
, 2) 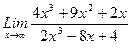 , 3)
, 3) 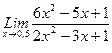 .
.
2. Найти производные первого порядка данных функций, используя правила вычисления производных 
1) 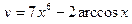 , 2)
, 2) 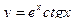 , 3)
, 3) 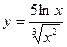 , 4)
, 4) 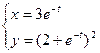 .
.
3. Построить график функции y=f(x), используя схему исследования функции
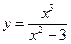 .
.
VI . ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К ЭКЗАМЕНУ
Вопросы для подготовки к экзамену (1-й семестр)
1. Определители. Свойства определителей.
2. Нахождение определителя путем разложения его по строке или столбцу.
3. Нахождение определителя путем сведения его к треугольному виду.
4. Матрицы. Действия над матрицами (сложение матриц, умножение матрицы на число, транспонирование матриц, умножение матриц). Свойства матриц.
5. Обратная матрица.
6. Системы линейных алгебраических уравнений (однородные, не однородные).
7. Решение систем линейных алгебраических уравнений (однородных, не однородных) по формулам Крамера.
8. Решение систем линейных алгебраических уравнений матричным методом.
9. Решение систем линейных алгебраических уравнений методом Гаусса.
10. Векторы. Действия с векторами (сложение векторов, умножение вектора на число).
11. Координаты вектора. Длина вектора. Действия с векторами, заданными координатами (сложение векторов, умножение вектора на число).
12. Разложение вектора по базису.
13. Скалярное произведение векторов.
14. Скалярное произведение векторов. Свойства скалярного произведения векторов.
15. Условия коллинеарности векторов. Условие ортогональности (перпендикулярности) векторов.
16. Направляющие косинусы.
17. Координаты вектора в полярной системе координат. Связь между полярными и прямоугольными координатами вектора.
18. Векторное произведение векторов. Свойства векторного произведения векторов.
19. Смешанное произведение векторов. Свойства смешанного произведения векторов.
20. Каноническое уравнение прямой на плоскости.
21. Уравнение прямой на плоскости, проходящей через две точки.
22. Уравнение прямой на плоскости с угловым коэффициентом.
23. Уравнение прямой на плоскости в отрезках.
24. Общее уравнение прямой на плоскости.
25. Угол между прямыми на плоскости.
26. Условия параллельности и перпендикулярности прямых на плоскости.
27. Уравнение плоскости, проходящей через три точки.
28. Уравнение плоскости, проходящей через две точки, параллельно заданному вектору.
29. Уравнение плоскости, проходящей через одну точку, параллельно двум векторам.
30. Общее уравнение плоскости.
31. Условия параллельности и перпендикулярности плоскостей.
32. Угол между плоскостями.
33. Каноническое уравнение прямой в пространстве.
34. Уравнение прямой в пространстве, проходящей через две точки.
35. Параметрическое уравнение прямой в пространстве.
36. Условия параллельности и перпендикулярности прямых в пространстве.
37. Условия параллельности и перпендикулярности прямой и плоскости.
38. Угол между прямой и плоскостью.
39. Эллипс. Каноническое уравнение эллипса.
40. Окружность. Уравнение окружности.
41. Гипербола. Каноническое уравнение гиперболы.
42. Парабола. Каноническое уравнение параболы.
43. Функция. Определения. Формы задания.
44. Преобразования графиков функций.
45. Числовая последовательность. Предел последовательности. Правила вычисления пределов последовательностей.
46. Предел функции. Правила вычисления пределов функций.
47. Свойства пределов функций (теоремы 6 – 10).
48. Неопределенности при вычислении пределов функций и их устранение.
49. Бесконечно большие и бесконечно малые функции. Свойства бесконечно малых функций (теоремы 1 – 5).
50. Производная функции. Геометрический и механический смысл производной.
51. Правила дифференцирования.
52. Производная сложной функции.
53. Производная обратной функции.
54. Производная параметрической функции.
55. Производная неявно заданной функции.
56. Дифференциал функции. Геометрический смысл дифференциала.
57. Производные и дифференциалов высших порядков.
58. Теорема Ролля (о корнях производной) (теорема 12).
59. Теорема Лагранжа (о конечных приращениях) (теорема 13).
60. Теорема Коши (об отношениях приращений двух функций) (теоре- ма 14).
61. Правило Лопиталя (теорема 15). Использование правила Лопиталя для устранения неопределенностей типа 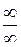 ,
,  .
.
62. Формула Тейлора. Формула Маклорена.
63. Разложение по формуле Маклорена функций: y = e x , y = sin x , y = cos x , y = ln ( 1 + x ) , y = ( 1 + x ) m .
64. Возрастающие и убывающие функции. Теорема о производной возрастающих и убывающих функций (теорема 16).
65. Точки экстремума функции. Необходимое условие существования экстремума функции (теорема 17).
66. Достаточные условия существования экстремума функции (теоре- ма 18).
67. Исследование функций на экстремум с помощью второй производной.
68. Наибольшее и наименьшее значения функции на отрезке.
69. Выпуклость и вогнутость графика функции (теорема 19). Точки перегиба.
70. Асимптоты графика функции.
71. Общая схема исследования функций.
72. Первый замечательный предел. Второй замечательный предел.
73. Непрерывность функции. Свойства непрерывных функций. Точки разрыва функции. Классификация точек разрыва.
74. Теорема о необходимом условии дифференцируемости функции (теорема 11).
Вопросы для подготовки к экзамену (2-й семестр)
1. Комплексные числа. Действия с комплексными числами.
2. Формула Муавра.
3. Разложение дробей на простейшие.
4. Неопределенный интеграл. Свойства неопределенных интегралов.
5. Методы интегрирования. Метод замены переменных в неопределенном интеграле.
6. Методы интегрирования. Интегрирование по частям в неопределенном интеграле.
7. Интегрирование рациональных функций.
8. Интегрирование некоторых тригонометрических функций.
9. Интегрирование некоторых иррациональных функций.
10. Интегрирование иррациональных функций с помощью тригонометрических подстановок.
11. Интегрирование иррациональных функций с помощью универсальной тригонометрической подстановки.
12. Определенный интеграл.
13. Свойства определенных интегралов (с доказательством).
14. Определенный интеграл с переменным верхним пределом (теорема).
15. Вычисление определенных интегралов. Формула Ньютона-Лейбница (теорема).
16. Интегрирование по частям в определенных интегралах.
17. Метод замены переменных в определенном интеграле.
18. Геометрические приложения определенных интегралов (вычисление площади фигуры, длины кривой, объема тела вращения вокруг оси Ох и вокруг оси Оу ).
19. Несобственные интегралы I рода.
20. Несобственные интегралы II рода.
21. Функции многих переменных. Основные понятия. Способы задания.
22. Предел функции двух переменных. Непрерывность функции двух переменных.
23. Частные приращения функции двух переменных. Полное приращение функции двух переменных.
24. Частные производные функции двух переменных. Частные и полные дифференциалы функции двух переменных.
25. Частные производные высших порядков функции двух переменных.
26. Производная по направлению функции трех переменных.
27. Градиент функции трех переменных. Связь градиента функции трех переменных с производной по направлению.
28. Экстремум функции нескольких переменных.
29. Нахождение наибольшего и наименьшего значений функции нескольких переменных в области.
30. Двойной интеграл.
31. Вычисление двойных интегралов путем сведения их к повторному.
32. Вычисление объемов тел с помощью двойного интеграла.
33. Криволинейные интегралы 1 рода и их свойства. Вычисление криволинейных интегралов 1 рода.
34. Криволинейные интегралы 2 рода и их свойства. Вычисление криволинейных интегралов 2 рода.
35. Формула Грина.
Вопросы для подготовки к экзамену (3-й семестр)
1. Задачи, приводящие к дифференциальным уравнениям.
2. Дифференциальное уравнение первого порядка. Общее и частное решение дифференциального уравнения первого порядка. Интегральные кривые.
3. Теорема Коши. Задача Коши и ее геометрическая интерпретация.
4. Дифференциальные уравнения с разделяющимися переменными.
5. Однородные дифференциальные уравнения первого порядка.
6. Линейные дифференциальные уравнения первого порядка.
Уравнения Бернулли.
7. Дифференциальные уравнения высших порядков, их решения.
Задача Коши.
8. Дифференциальные уравнения второго порядка, допускающие понижения порядка.
9. Линейные дифференциальные уравнения высших порядков с постоянными коэффициентами. Основные понятия.
10. Решение однородных линейных дифференциальных уравнений высших порядков с постоянными коэффициентами.
11. Решение неоднородных линейных дифференциальных уравнений высших порядков с постоянными коэффициентами и специальной правой частью.
12. Решение неоднородных линейных дифференциальных уравнений высших порядков методом вариации произвольной постоянной.
13. Числовые ряды. Сходимость числового ряда. Свойства сходящихся числовых рядов.
14. Необходимый признак сходимости знакоположительного ряда.
15. Достаточный признак расходимости ряда.
16. Достаточные признаки сходимости знакоположительных рядов: признак Даламбера, признак Коши, интегральный признак.
17. Знакопеременные и знакочередующиеся ряды.
18. Признак Лейбница. Исследование сходимости знакочередующихся рядов.
19. Степенной ряд, область его сходимости. Свойства степенных рядов
20. Теорема Абеля.
21. Интервал и радиус сходимости степенного ряда. Исследование сходимости степенных рядов.
22. Ряд Тейлора. Остаточный член ряда Тейлора. Ряд Маклорена.
23. Разложение некоторых элементарных функций в ряды Тейлора и Маклорена.
VI . ЛИТЕРАТУРА, РЕКОМЕНДУЕМАЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ ПРИ ИЗУЧЕНИИ ДИСЦИПЛИНЫ
а) основная литература:
1. Пискунов Н.С. Дифференциальное и интегральное исчисление для вузов. Т.1. Учебное пособие для вузов. – М.: Наука, Главная редакция Физико-математической литературы, 2013. – 432 с.
2.. Пискунов Н.С. Дифференциальное и интегральное исчисление для вузов. Т.2: Учебное пособие для вузов. – М.: Наука, Главная редакция Физико-математической литературы, 2010. – 560 с.
3. Клетеник Д.В. Сборник задач по аналитической геометрии: Учебное пособие для вузов. – М.: Наука, Главная редакция физико-математической литературы, 2002. – 224 с.
4. Демидович Б.П. Задачи и упражнения по математическому анализу для втузов. Учебное пособие для втузов. – М.: Наука, Главная редакция физико-математической литературы, 2016. – 472 с
б) дополнительная литература:
1. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Часть 1. – М.: Высшая математика, 2001. – 304 с.
2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Часть 2. – М.: Высшая математика, 2001. – 284 с.
3. Кручкович Г.И. Сборник задач по курсу высшей математики. – М.: Высшая школа, 2003. – 277 с.
4. Лунгу К.Н. Сборник задач по высшей математике. – М.: Айрис-пресс, 2004. – 592 с.:
5. Письменный Д.П. Конспект лекций по высшей математике. В 2-х частях.– М.: Айрис-пресс, 2006 – 256 с..
6. Шипачев В.С. Высшая математика. – М.: Высшая школа, 2001. – 372 с.
8. Шипачев В.С Задачник по высшей математике. – М.: Высшая школа, 2004. – 324 с.:
1. Берман Г.Н. Сборник задач по курсу математического анализа: Учебное пособие для вузов. – М.: Наука. Главная редакция физико-математической литературы, 2001. – 384 с.
9. Гальченко В.Т, Высшая математика в упражнениях и задачах – Новогорск: АГЗ МЧС России, 2012. –110с.
ОГЛАВЛЕНИЕ
Введение…………………………………………………………………..
I. Тематический план……………………………………………………….
II. Содержание учебных занятий…………………………………………...
III. Методические рекомендации по изучению дисциплины……………..
IV. Задания домашней контрольной работы……………………………….
V. Вопросы для подготовки к экзамену……………………………………
VI. Литература, рекомендуемая для самостоятельной работы при изучении дисциплины……………………………………………………
Министерство Российской Федерации
по делам гражданской обороны, чрезвычайным ситуациям
Дата: 2019-07-24, просмотров: 275.