Комбинаторно-морфологический метод синтеза может быть эффективно применен для решения задач функционально-стоимостного анализа и прогнозирования систем. При этом предполагается, что исследуемая система улучшается одновременно по нескольким или всем функциям и по каждой функции имеет более одной альтернативы по ее реализации.

Рассмотрим наиболее характерные случаи синтеза рациональных решений на морфологических таблицах при условии, что в искомое решение обязательно включается по одной альтернативе по всем имеющимся в таблице функциям, т.е. из каждой строки таблицы.

Случай 1. Каждая альтернатива А _ij морфологической таблицы имеет оценку ее выгод (достигаемой эффективности) и оценку требуемых для реализации издержек, которые выражены в денежных единицах, т.е. каждой А _ij Î {B_ij; И _ij}, где B_ij, И _ij — значения в денежных единицах выгод и издержек.

Поиск рациональных вариантов решений может быть осуществлен в соответствии со следующими постановками задач.

1. Найти решения, удовлетворяющие одной из приведенных целевых функций:

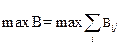
где В, И — значения выгод и издержек для m-го целостного решения;

B_ij, И _ij — значения выгод и издержек альтернативы А _ij (i = 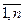, п — число строк морфологической таблицы; j = 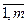, для i = l; j = 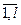, для i = 2; j =  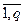для i = п).

2. Найти одно или несколько решений, удовлетворяющих целевой функции

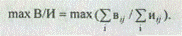
3. Найти одно или несколько решений по отношению выгод к издержкам, удовлетворяющих целевой функции и ограничениям:

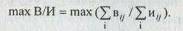
На целевую функцию может быть наложено одно из приведенных ограничений:

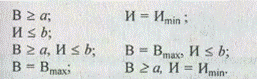
Здесь а и b — пороговые значения (ограничения) выгод и издержек, выраженные в денежных единицах.

Случай 2. Каждая альтернатива А_ij морфологической таблицы имеет только экспертную оценку выгод и издержек. Т.е. А _ij Î {v_ij^B, v_ij ^И}, верхние индексы характеризуют соответственно выгоды (В) и издержки (И).

Поиск рациональных решений осуществляется по следующим целевым функциям.

1. Найти решения, удовлетворяющие одной из приведенных целевых функций

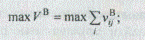
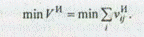
Здесь V^В, V ^И — значения выгод и издержек для т-го целостного решения, каждая альтернатива А _ij которого охарактеризована экспертными значениями v_ij^B, v_ij ^И (в частности, значениями нормированного вектора приоритета альтернатив по критерию качества); i = 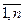 (п — число строк морфологической таблицы); j =  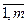для i = 1; j =  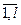для i =2; j =  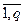для i = n.

2. Найти рациональные решения по отношению выгод к издержкам, представленному в целевой функции экспертными данными:

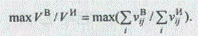
С учетом накладываемых на целевую функцию ограничений имеем:

при выполнении одного из приведенных ограничений:

Здесь a^ç, b^ç — ограничения (пороговые значения) выгод и издержек, выраженные в безразмерной шкале экспертных оценок.

При этом в общем случае значения v_ij^B и v_ij ^И представляют интегральные оценки, принадлежащие вектору приоритетов элементов (альтернатив) i-й строки матрицы по экономическим, техническим, социальным, управленческим и другим факторам. Данные векторы рассчитываются для каждой строки морфологической матрицы методами анализа иерархических систем.

Случай 3. Каждая альтернатива А _ij морфологической матрицы имеет экспертную оценку для оценки выгод (неопределенность по выгодам) от ее реализации и оценку издержек в денежных единицах, т. е.А _ij Î { v_ij^B, И _ij }.

Поиск рациональных решений осуществляется по следующей целевой функции: найти рациональные решения по отношению выгод, выраженных экспортно, к издержкам, определенным в денежных единицах:

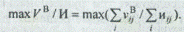
На целевую функцию может быть наложено одно из приведенных ниже ограничений:

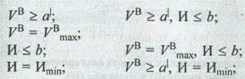
Обозначения в целевых функциях и ограничениях соответствуют вышепринятым.

Случай 4. Каждая альтернатива А _ij морфологической матрицы имеет оценку выгод в денежном выражении и экспертную оценку издержек (неопределенность по издержкам), т.е. А _ij Î {в_ij, v_ij ^И }.

Поиск рациональных решений осуществляется по следующей целевой функции: найти рациональные решения по отношению выгод, выраженных в денежных единицах, к издержкам, определенным экспортно:

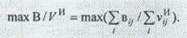
На целевую функцию может быть наложено одно из приведенных ниже ограничений:

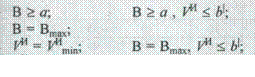
При решении практических задач число искомых рациональных решений задается исследователем и может находиться в пределах от одного до нескольких десятков в зависимости от размерности задачи и конкретных условий ее решения.

Рассмотрим подходы по применению комбинаторно-морфологического метода для проведения функционально-стоимостного анализа систем.

Пусть имеется морфологическая таблица, описывающая множество систем (табл. 5.26).

Каждая система содержит три функциональные подсистемы F,. Подсистемы имеют альтернативные решения, для которых известны значения выгод и издержек, выраженные в денежных единицах (млн руб.) — случай 1. Предположим, требуется синтезировать виброзащитную систему, удовлетворяющую целевой функции:

max В/И при условии В = Вmах.                          (5.18)

Таблица 5.26

Морфологическая таблица с оценкой альтернатив по критериям выгод (В) и издержек (И)

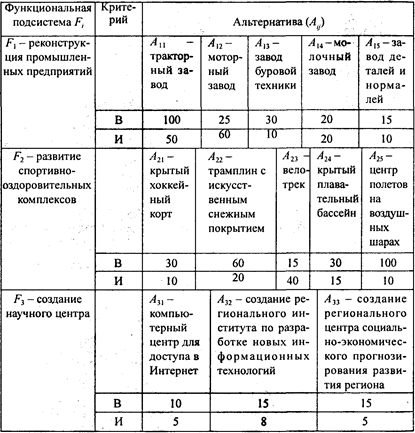
Поиск решений на морфологической матрице методом сканирования позволяет выявить два решения, обеспечивающих максимальную выгоду в размере 215 млн руб.: (А₁₁А₂₅А₃₂) и (А₁₁А₂₅ A ₃₃). Однако отношение выгод к издержкам у первого и второго вариантов решения различны и составляют соответственно 215/68 и 215/65. Следовательно, искомым решением является второе.

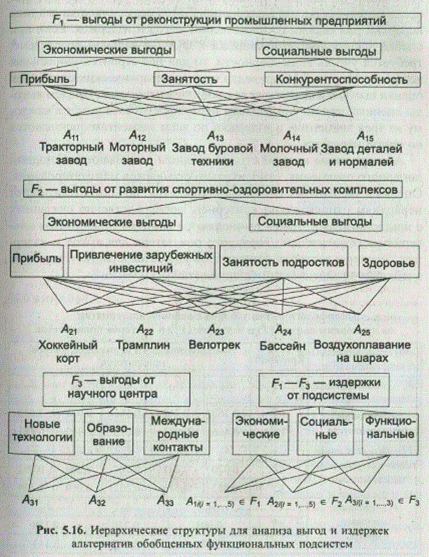
Для проведения функционально-стоимостного анализа систем в ситуациях, когда отсутствуют количественные данные в денежном выражении по выгодам и издержкам (случай 2), осуществляется предварительная оценка альтернатив. С этой целью строятся два типа иерархий для оценки соответственно выгод и издержек. Если при оценке альтернатив, относящихся к функциональной подсистеме, требуется учесть ее особенности, то для нее строится уникальная иерархия. На рис. 5.16 приведен пример иерархических систем для оценки выгод и издержек от реализации альтернатив. Причем выгоды оцениваются по уникальным иерархиям, относящимся к каждому из трех элементов, а издержки по всем элементам оцениваются по одной иерархии.

Альтернативы каждой строки таблицы оцениваются методами попарного сравнения, относительно стандартов или копирования. Оценка в экспертных единицах проводится по соответствующим иерархиям относительно критериев, непосредственно связанных с альтернативами. Далее вычисляются векторы приоритетов альтернатив относительно корневого показателя для выгод и издержек. Значения векторов приоритетов заносятся в соответствующие ячейки морфологической таблицы (табл. 5.27).

Таблица 5.27

Морфологическая таблица с оценкой альтернатив по критериям выгод (V ^B ) и издержек ( V ^И ) и векторов приоритетов

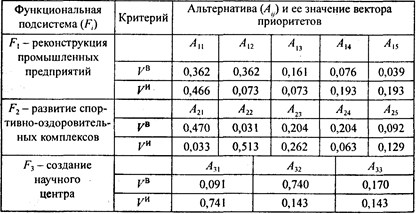
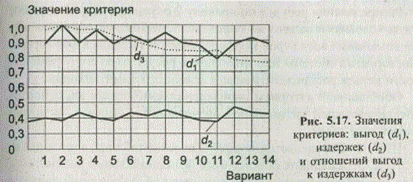
Поиск решений, удовлетворяющих заданной целевой функции max V ^В / V ^И , может проводиться по одному из алгоритмов, приведенных в этой главе. На рис. 5.17 показаны абсолютные значения критериев: выгод (d ₁) и издержек (d ₂) и относительные значения отношений выгод к издержкам (d ₃) для 14 наилучших вариантов, синтезированных на рассматриваемой морфологической таблице. Относительные значения d ₃ получены путем деления отношений d ₁ / d ₂ , принадлежащих синтезированным вариантам, на максимальное значение (d ₁/d ₂) max.