Рассмотрим метод принятия решений, предполагающий построение множества недоминируемых альтернатив на основе нечеткого отношения предпочтения [З].
Постановка задачи в краткой форме представляется следующим образом. Пусть задано множество альтернатив А и каждая альтернатива характеризуется несколькими критериями качества с номерами j == i, ..., т. Информация о попарном сравнении альтернатив по каждому критерию качества j представлена в форме отношения предпочтения Rj . Таким образом, имеется т отношений предпочтения Rj на множестве А. Требуется выбрать лучшую альтернативу из множества {A , R 1 , ...,Rm}.
Метод многокритериального выбора альтернатив на основе нечеткого отношения предпочтения основан на ряде определений.
Определение 1. Нечетким отношением R на множестве А называется нечеткое подмножество декартова произведения А ´ А, характеризующееся функцией принадлежности mR: А ´ А ® [0,1]. Значение mR (a, b) этой функции понимается как степень выполнения отношения а Ù b .
Определение 2. Нечетким отношением предпочтения на А называется любое заданное на этом множестве рефлексивное нечеткое отношение, функция принадлежности которого вычисляется следующим образом:

Определение 3. Пусть А — множество альтернатив и mR — заданное на нем нечеткое отношение предпочтения. Нечеткое подмножество недоминируемых альтернатив множества (А, mR) описывается функцией принадлежности

Определение 4. Четко недоминируемыми называются альтернативы, для которых mRНД (а) = 1, а множество таких альтернатив
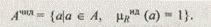
Определение 5. Носителем нечеткого множества В с функцией принадлежности mB (a) является множество {а½а Î А, mB > 0}.
Процедура решения задачи выбора выполняется в несколько шагов.
1. Строится нечеткое отношение Q 1 , которое является пересечением исходных отношений предпочтения:
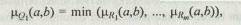
и определяется нечеткое подмножество недоминируемых альтернатив в множестве (А, mQ1):

2. Строится нечеткое отношение Q 2 :
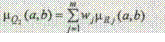
и определяется нечеткое подмножество недоминируемых альтернатив в множестве ( A ,mQ2):

Данная функция упорядочивает альтернативы по степени их недоминируемости. Числа wj в приведенной выше свертке представляют собой коэффициенты относительной важности рассматриваемых критериев, для которых выполняются следующие условия:
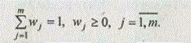
3. Отыскивается пересечение множеств mQ1НД и mQ2НД:

4. Рациональным считается выбор альтернатив из множества

Наиболее рациональной альтернативой из множества АНД является та, которая имеет максимальную степень недоминируемости.
Дата: 2019-04-23, просмотров: 319.