Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

1. res_size ::= 2 * y_size ; max_offset ::= y_size – psi_zise;
null_offset ::= min{psi_size – 1, res_size}; i ::= 0;

2. Если i ≥ null_offset, то переход к п.3;

3. res_i ::= 0; i ::= i + 1; переход к п. 2;

4. Если null_offset = res_size, то переход к п. 14;

5. i ::= 0;

6. Если i > max_offset, то переход к п. 11;

7. sum ::= 0; j ::= 0;

8. Если j ≥ psi_size, то переход к п. 9

9. sum ::= sum + y_i+j * psi_j; j ::= j + 1; переход к п. 8

10. res_{2*i+psi_size-1} ::= sum; res_{2*i+psi_size} ::= 0; i ::= i+1; переход к п. 6

11. i ::= res_size – null_offset;

12. Если i ≥ res_size, то переход к п. 14;

13. res_i ::= 0; i ::= i + 1; переход к п.12;

14. Конец.

 

2.3.6. Требования к контрольному примеру

Контрольный пример должен содержать результаты перемножений сигнала с вейвелетами различных масштабов.

 

Список условных обозначений

Алгоритм использует следующие условные обозначения:

y – анализируемый сигнал;

y_size – размер анализируемого сигнала;

psi – дискретизированный вейвлет;

psi_size – размер дискретизированного вейвлета;

res – резельтат переменожения сигнала и вейвлета;

res_size – размер результата.

 

Описание алгоритма вейвлет-анализа

 

Назначение и характеристика алгоритма вейвлет-анализа

Вейвлет-анализ является инструментом, разбивающим данные на составляющие с различными частотами, каждая из которых затем изучается с разрешением, подходящим масштабу. Алгоритм ортогонального вейвелет-анализа, который реализован в данной работе, предназначен для анализа дискретных сигналов в различных масштабах посредством передискретизации ортогонального вейвлета.

 

Используемая информация

При реализации алгоритма используются размерные характеристики сигнала и вейвлета, а также их значения.

 

Результаты решения

Результатами решения является матрица, каждую точку которой можно сопоставить конкретному значению входного сигнала и конкретному масштабу вейвлета.

 

Математическое описание алгоритма вейвлет-анализа

 

Обобщенное математическое описание вейвлет-анализа приведено в п. 2.1.4.3. Как и в п. 2.3.4, количество точек в строке удваивается. Вследствие этого, исходя из формулы (2.4), получаем следующее:

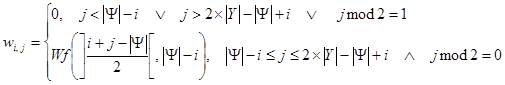, (2.6)

где 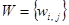, , 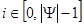 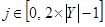– результат вейвлет-анализа;

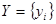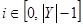,  – исходный сигнал;

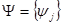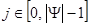,  – вейвелет;

 – модуль (длина) вектора;

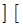 – взятие целой части;

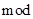 – остаток от целочисленного деления;

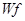 – функция вейвлет-анализа, описанная в формуле (2.4);

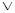 – логическое «или»;

 – логическое «и».

 

Алгоритм вейвлет-анализа

 

1. i ::= 0;

2. Если i ≥ psi_size, то переход к п. 4;

3. psi_scaled ::= resample(psi, psi_size – i);
res_i ::= multiply(y, psi_scaled);
i ::= i + 1;

4. Конец.

2.4.6. Требования к контрольному примеру

Контрольный пример должен содержать результаты вейвлет-анализа сигнала, состоящего не менее чем из двух нестационарных составляющих, при помощи вейвлетов, соизмеримых по масштабу с составляющими сигнала.

Список условных обозначений

Алгоритм использует следующие условные обозначения:

y – анализируемый сигнал;

psi – дискретизированнный исходный вейвлет;

psi_size – размер исходного вейвлета;

psi_scaled – смаштабированный (передискретизированный) вейвлет;

res – результат вейвлет анализа;

resample – оператор передискретизации вейвлета (см. п. 2.2);

multiply – оператор перемножения сигнала (см. п. 2.3).