Математическое описание передискретизации сигнала приведено в п.

2.1.4.1. Результирующий сигнал рассчитывается по формуле (2.2).

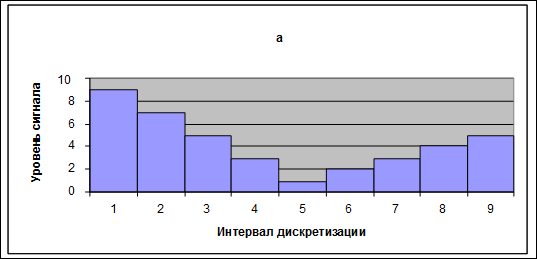
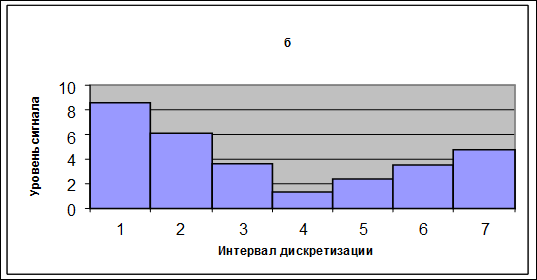
Пример передискретизации сигнала изображен на рис. 2.1.

Пример передискретизации сигнала

	а – дискретизация сигнала на 9 интервалов б – дискретизация сигнала на 7 интервалов Рис. 2.1

Алгоритм передискретизации сигнала

1. i ::= 0; offs ::= 0;

2. Если i ≥ res_size, то переход к п. 7;

3. res_i ::= 0; j :: = 0;

4. Если j ≥ src_size, то переход к п. 6;

5. res_i ::= res_i + src_{](offs + j) / res_size[}; j ::= j + 1; переход к п. 4;

6. res_i ::= res_i / src_size; i ::= i + 1; offs ::= offs + src_size; переход к п. 2;

7. Конец.

2.2.6. Требования к контрольному примеру

Контрольный пример должен содержать результаты передискретизации сигнала в масштабах от исходного размера до 1.

Список условных обозначений

Алгоритм использует следующие условные обозначения:

src – исходный сигнал;

src_size – размер исходного сигнала;

res – передискретизированный сигнал;

res_size – размер результата передискретизации;

][ – взятие целой части.

Описание алгоритма перемножения сигнала и вейвлета

Назначение и характеристика алгоритма перемножения сигнала и вейвлета

Данный алгоритм предназначен для усреднения значений сигнала с использованием вейвлета определенного масштаба. Усреднение заключается в анализе каждого значения сигнала в его окрестностях, причем размер окрестностей и есть ни что иное, как размер вейвлета.

Используемая информация

При реализации алгоритма используются размерные характеристики сигнала и вейвлета, а также их значения.

Результаты решения

В результате перемножения получается массив вещественных чисел с ярко выраженными максимумами и минимумами, соответсвующими степени идентичности значений сигнала вейвлету заданного масштаба.

Математическое описание алгоритма перемножения сигнала и вейвлета

Обобщенное математическое описание перемножения сигнала и вейвлета приведено в п. 2.1.4.2. Для ускорения расчёта и обработки размер результата искусственно увеличим вдвое. Данное допущение также решит проблемы с четностью/нечетностью размеров вейвлета и сигнала.

Итак, если применить удвоение результата к отмеченным в п. 2.1.4.2 формулировкам, исходя из формулы (2.3), имеем следующий результат перемножения:

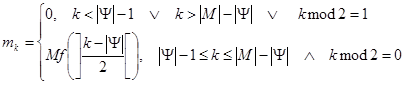       ,       (2.5)

где 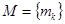, , 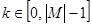 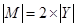– результат перемножения;

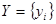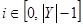,  – исходный сигнал;

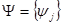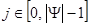,  – вейвелет;

 – модуль (длина) вектора;

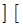 – взятие целой части;

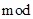 – остаток от целочисленного деления;

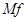 – функция перемножения, описанная в формуле (2.3);

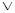 – логическое «или»;

 – логическое «и».